梁菊先,鐘裕林

(1.河北北方學(xué)院理學(xué)院,河北張家口075000;2.海南軟件職業(yè)技術(shù)學(xué)院,海南瓊海571400)

1 引 言

本文沿用文獻(xiàn) [1-3]中的術(shù)語和符號.在文獻(xiàn) [3]中給出了有限集合的所有子集作成的格及其特征多項式.在文獻(xiàn) [1]和 [2]對子空間軌道生成的格進(jìn)行了詳細(xì)的討論.得出一些重要結(jié)果.本文采用文獻(xiàn) [1]中討論問題的方法,給出了有限集的所有排列作成的格,討論了它們的包含關(guān)系,給出格中元素的刻畫及它的特征多項式.

設(shè) P是一個非空集,≤是定義在 P上的一個二元關(guān)系.如果下列的三條公理P01-P03成立,P就叫做一個偏序集,≤就叫做 P上的偏序.

P01對于任意 x∈P,都有 x≤x.

P02對于任意 x,y∈P,如果 x≤y,而且 y≤x,那么 x=y.

P03對于任意 x,y,z∈P,如果 x≤y,而且 y≤z,那么 x≤z.

P上的偏序≤有時記作≥,如果 x≤y,而 x≠y,就記 x＜y(或 y＞x).

設(shè) P是一個偏序集,a,b∈P,a＜b,如果不存在c∈P,使得 a＜c＜b.則稱b是a的覆蓋,記作 a＜·b.P中的元素m叫做 P的一個極小 (大)元,如果不存在 x∈P,使得 x＜m(x＞m).如果對所有x∈P,都有 m＞x(m＜x),則 m叫做 P的最大 (小)元.P中唯一的最大 (小)元記作1(0).

對于 x,y∈P,x＜y.如果存在 x=x0,x1,…,xn=y,使得

把 (1)叫做以 x為起點,y為終點的鏈,也叫 x,y鏈,而 n叫做它的長.如果 xi＜·xi+1(i=0,1,…,n-1),(1)就叫做 x,y的極大鏈.如果

也是 x,y的鏈.而 Xi(1≤i≤n)都在 (2)中出現(xiàn),則 (2)就叫做 (1)的加細(xì).設(shè) P是包含0的偏序集,如果0,a鏈都可加細(xì)成極大鏈,并且所有極大鏈有相同的長,就把這相同的長記作r(a).

定義1 設(shè) P是包含0的偏序集,0是非負(fù)整數(shù)所成的集合.函數(shù) r∶P→0;a叫 P上的秩函數(shù).如果下面的 (i)和 (ii)成立.

(i)r(0) =0

(ii)對于 a,b∈P,而 a＜·b,那么 r(b) =r(a) +1.

設(shè) T是偏序集的一個子集,u∈P,如果對所有 x∈T都有u≥x(≤x),u就叫做 T的一個上 (下)界,如果 u是 T的一個上界,而對 T的任一個上界v,都有 v≥u,那么 u就叫做 T上確界.同樣可以定義下確界.

偏序集L稱為格,如果L中任意兩個元素都有上確界和下確界.把L中元素a和b的上確界和下確界分別記為a∨b和a∧b,分別讀作 a并b和a交b.當(dāng)格L含有有限個元素時,就稱為有限格.

設(shè)L是包含0的偏序集.覆蓋0的元素稱為L的原子,包含0的格稱為原子格,如果對每個 a∈L{0},a都是L中一些原子的上確界,即

定義2 設(shè)L是包含0的有限格,L叫做幾何格,如果滿足以下的條件:

(i)L是一個原子格;

(ii)L具有秩函數(shù)r,而且對所有的 x,y∈L,都有

定義3 設(shè) P是有限偏序集,K是特征數(shù)為0的域,并且μ(x,y)是定義在 P上而在 K中取值的二元函數(shù).假定μ(x,y)滿足以下三個條件:

(i)對任意 x∈P,總有μ(x,x) =1;

(ii)對于 x,y∈P,如果 x∈y,則μ (x,y) =0;

(iii)對于 x,y∈P,如果 x＜y,則∑x≤z≤yμ(x,z) =0,就把μ (x,y)叫做 P上而在 K中取值的M?bius函數(shù).

定義4 設(shè) P是包含0和1的有限偏序集,并且 P上有秩函數(shù)r和M?bius函數(shù)μ,那么多項式

叫做 P上的特征多項式.

2 n元有序集的排列作成的格

設(shè)A (n)={1,2,…,n}是n個元素的一個全序集 (其序按自然數(shù)的大小順序),是 A (n)的 k元排列 (i1,i2,…,ik),k=0,1,2,…,n,記為Ak.約定0元排列A0是空集?.A (n)的n元排列共有n!個,Ak= {i1,i2,…,ik}的的子排列Al指的是Ak的一個子集,并且按Ak的序得到A (n)的一個排列 (ji,j2, …,jl),記為 {ji,j2, …,jl} ? {i1,i2, …,ik},即Al?Ak.

令￡(A (n))是以An的所有k(k=0,1,2,…,n)元排列為元素組成的集合,對于 Ak,Al∈￡ (A (n)),如果Ak?Al,就定義 Al≤Ak.那么≤是￡ (A (n))的一個偏序關(guān)系,￡ (A (n))是一個有限偏序集,并且?和A (n)分別是它的最大元和最小元.對于 Ak,Al∈￡(A (n)),定義 Ak∩Al是它們公共元按A (n)的序所成的排列,Ak∪Al是Ak和Al中元的并按A (n)的序所成的排列.顯然,Ak∩Al,Ak∪Al∈￡ (A (n)).再定義 Ak∨Al=Ak∩Al,Ak∧Al=Ak∪Al,那么￡ (A (n))對于所定義的∨和∧封閉.因而作成一個有限格,記為￡R(A (n)),稱為 A (n)的排列按反包含關(guān)系生成的格.

3 重要結(jié)果

引理1 設(shè)A (n) = {1,2,…,n}是n個元素 (簡稱 n元)的全序集,￡R(A (n))是由A (n)的排列按反包含關(guān)系生成的格,那么|￡R(A (n)) |=

證明 因為A (n)的 k元排列Ak的個數(shù)是n(n-1) … (n-k+1),k=0,1,…,n,而￡R(A(n))是由A (n)的所有排列組合的集合,所以|￡R(A (n)) |=1+n+n(n-1) +…+n(n-1)…(n-k+1) +n!而n(n-1) …(n-k+1)因此|￡R(A (n)) |=

定理2 n＞1,X∈￡R(A (n)).定義

那么 r′∶￡R(A (n)) →0是格￡R(A (n))的秩函數(shù),并且￡R(A (n))是幾何格.

證明 前面已給出的￡R(A (n))是一個格.現(xiàn)在證明 (3)是￡R(A (n))的秩函數(shù).顯然,r(A (n)) =0.令 X,Y∈￡R(A (n)),X＜·Y,而 X= (i1,i2,…,ik),Y= (j1,j2,…,jl),那么 Y是 X的子排列,|X|=|Y|+1.由 (3),有 r′(Y) =n- (k-1) =n-k+1,r′(X) =nk.所以 r′(Y) =r′(X) +1.因此 r′是格￡R(A (n))的秩函數(shù).

下面證明 ￡R(A(n))的幾何性.令{^i}=A(n) {i},i=1,2,…,n,那么(1^),(2^,…,(^n)是 ￡R(A(n))的原子,?X∈￡(A(n)),記=(i,i,…,i),那么=(i)∪(i)∪…∪(i),因而 X=∩…∩(^i)R12l12ll因此 ,在 ￡(A(n))中(i)成立.R

設(shè) X,Y∈￡R(A (n)),當(dāng)≠A (n),Y≠A (n)時,令 X= (i1,i2,…,ik),Y= (j1,j2,…,jl),那么 r′(X) =n-k,r′(Y) =n-l,因為 X∩Y是 (1,2,…,n)包含在 X,Y中元數(shù)最多的t元排列 (h1,h2,…,ht),而 X∪Y是 (1,2,…,n)包含 X,Y中元數(shù)最少的 p元排列 (m1,m2,…,mp),所以 p=k+l-t,因而|X∪Y|=|X|+|Y|-|X∩Y|,|X∨Y|=|X|+|Y|-|X∧Y|.由 (3)式,有 r′(X∨Y) =n-|X∨Y|,r′(X∧Y) =n-|X∧Y|.所以

當(dāng) X=Y=A(n)時,顯然 r′(X∨Y)+r′(X∧Y)=r‘(X)+r‘(Y);當(dāng) X,Y中有一個是A(n),不妨設(shè) X=A(n).Y≠A(n),那么 X∨Y=Y,X∧Y=X,因而 (4)成立.因此,在￡R(A(n))中 (ii)成立.

綜上所述,￡R(A (n))是幾何格.

定理3 設(shè) n＞1,那么￡R(A (n))的特征多項式是

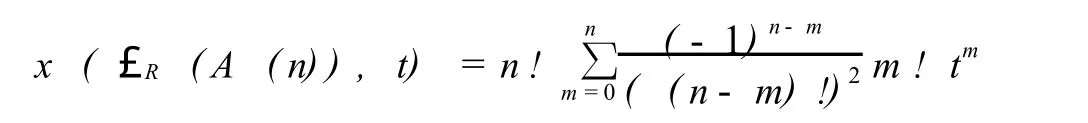
證明 因為?和A(n)分別是￡R(A(n))的最大元和最小元.設(shè) X,Y∈￡R(A(n)),定義

斷言(5)是 ￡R(A(n))的 M?bius函數(shù).實際上,μ(X,X)=1;并且 XY時,μ(X,Y)=0;當(dāng)|X|-|Y|=t時,如果 X＜Z≤Y,而|X|-|Z|=i,那么 Z的選取個數(shù)是,而μ(X,Z)=(-1)所以

因此上述的斷言成立.

由特征多項式的定義,對于 X,X′∈￡R(A (n)),如果|X|=|X′|=m,0≤m≤n,那么=tm. 因為 A (n) 含 m 個元的排列的個數(shù)是而μ (A (n),

定理4 設(shè) M(A(m,n))={X∈￡(A(n))||X|=m},1≤m≤n-1.由 M(A(m,n))中元素的交組成的集合記為￡(A (m,n)),并且約定A (n)是M(A (m,n))中零元素的交,如果按￡R(A (n))的偏序關(guān)系來規(guī)定￡(A(m,n))的偏序,即對于 X,Y∈￡(A(m,n)),如果Y是X的子排列,就規(guī)定 X≤Y,那么￡ (A (m,n))是一個有限格,記為￡R(A (m,n)).

證明 顯然|￡R(A(m,n))|＜∞,并且對于￡R(A (n))的偏序≤來說,￡R(A (m,n))是一個偏序集,而∩X∈￡R(A(m,n))X和A (n)分別是它的最大元和最小元,現(xiàn)在證明按照￡R(A (n))所定義的交和并是封閉的.任取 X1,X2∈￡R(A (m,n)).由 X1和 X2是 M(A (m,n))中元素的交,可知X1∨X2=X1∩X2∈￡R(A (m,n)).因為 X1∪X2?A (n),而 A (n) ∈￡R(A (m,n)),并且￡R(A (m,n))中包含 X1∪X2的元素的交也包含 X1∪X2,所以￡R(A (m,n))中有唯一包含 X1∪X2的最小者,因此 X1∧X2=∩{Z∈￡R(A (m,n)) |X1∪X2?Z} ∈￡R(A (m,n)).于是￡R(A(m,n))是一個有限格.

定理5 設(shè) n≥m≥0.

的充分必要條件是m≥m1≥0.

證明 充分性.當(dāng)n=1時,顯然 (6)成立.下面假設(shè) n≥2.我們來證明

設(shè) P∈M (m-1,n),P= (i1,i2,…,im-1).把A (n)中的元素添加到 P中,使得 (jt0,1,it0,2, …,jt0,t0,i1,jt1,1,jt1,2,…,jt1,t1,i2,…,im-1,jtm-1,1,jtm-1,2,…,jtm-1,tm-1) = (1,2,…,n),其中{jtk,1,jtk,2, …,jtk,tk},k=0,1,2, …,m-1,有可能是空集,因為n-m≥2,所以￡R(A (m,n))中有兩個不相同的子排列 P∪ (jtp,k)和 P∪ (jtq,h),jtp,k≠jtq,h},使得 P= (P∪ (jtp,k)) ∩ (P∪(jtq,h)) ∈￡R(A (m,n)),其中 k,h∈{1,2, …,l},l=t0,t1, …,tm-1,ip,iq∈{i0,i1, …,im-1}.因此 (8)成立,從而 (7)成立.

現(xiàn)在來證明 (6).當(dāng)m=m1時,顯然 (6)成立.下設(shè) m＞m1.由 (7),可得￡R(A (m,n)) ?￡R(A (m-1,n)) ?…?￡R(A (m1,n)).因此 (6)成立.

必要性.由M (A (m1,n)) ?￡R(A (m1,n)) ?￡R(A (m,n)),可知￡R(A (m,n))含A(n)的m1元排列Q,并且Q是M (A (m,n))中元素的交,所以在￡R(A(m,n))中存在A(n)的m元排列 P,使得 P?Q,因此 m≥m1≥0.

定理6 設(shè) n＞m≤0.那么￡R(A(m,n))由 A(n)和 A(n)的元數(shù)≤m的全體排列組成.

證明 由￡R(A(m,n))的定義,A(n)∈￡R(A(m,n)).因為￡R(A(m,n)) {A(n)}中的元素是 A(n)的含m個元的排列的交,所以對于 X∈￡(A(m,n)) {A(n)},有|X|≤m.

反之,設(shè) P是A (n)的 k元排列,0≤k≤m,那么 P∈M(A(k,n))?￡R(A(k,n)).由定理5,￡R(A(k,n))? ￡R(A(m,n)),所以 P∈￡R(A(m,n)).

推論7 設(shè) n＞m≥0,那么 ?∈￡R(A (m,n)).因而￡ (A (m,n))的最大元∩X∈￡(A(m,n))X=?.

推論8 ￡R(A (m+1,n)) =￡R(A (m+1)).

定理9 設(shè) n＞m≥0.那么￡R(A (m,n))的特征多項式

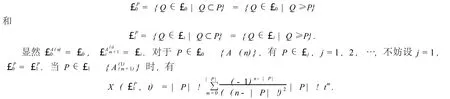
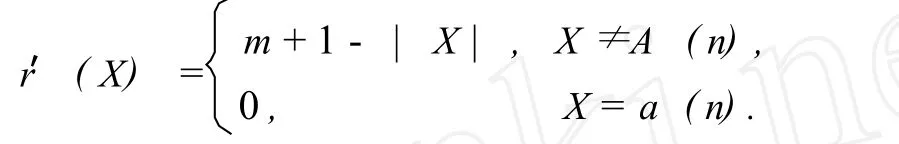
是￡1的秩函數(shù).因為￡0是有最大元 ?和最小元A (n)的有限格,而￡1是有最大元 ?和最小元A(1)m+1的有限格,所以￡0和￡1的特征多項式分別是

[1] 萬哲元,霍元極.有限典型子空間軌道生成的格 (第二版)[M].北京：科學(xué)出版社,2004：8-54

[2] Huo Y,Wan Z.On the geomertricity of lattices generated by orbits of subspaces under finite classical groups[J].Algebra,2001,243：339-359

[3] Aigener M.Combinatorial Theory[M].Berlin：Spring-Verlag,1979：1-40