含有指數(shù)和對數(shù)的函數(shù)不等式問題的求解策略
廣東省中山市中山紀(jì)念中學(xué)(528454) 李文東
同時含有指數(shù)和對數(shù)的函數(shù)的不等式問題是高考中的重點(diǎn)也是難點(diǎn)問題,此類問題常常在壓軸題的位置出現(xiàn),難度很大,而且直接求導(dǎo)后導(dǎo)函數(shù)往往比較復(fù)雜,只有少部分簡單類型能夠直接求導(dǎo)求解,其思考角度比較獨(dú)特.本文針對此類問題給出了常見的一些求解策略.
策略一:極值點(diǎn)在同一位置,直接求導(dǎo)判斷單調(diào)性
例1若不等式ex(2x3-3x2)-lnx-ax>1 恒成立,求實數(shù)a的取值范圍.
解ex(2x3-3x2)-lnx-ax>1 恒成立,分離參數(shù)得:a<ex(2x2-3x)-令f(x)=ex(2x2-3x)-則f′(x)=ex(2x+3)(x-1)+顯然f′(1)=0,且當(dāng)x>1 時,f′(x)>0,f(x) 遞增;當(dāng)0<x<1 時,f′(x)<0,f(x)遞減;故a<fmin(x)=f(1)=-e-1.
點(diǎn)評指數(shù)部分和對數(shù)部分的極值點(diǎn)在同一位置,可以直接判斷出函數(shù)的單調(diào)性,這屬于此類問題中比較簡單特殊的情形,求導(dǎo)后需要仔細(xì)觀察導(dǎo)函數(shù)即可!
策略二:虛設(shè)零點(diǎn),設(shè)而不求
例2已知函數(shù)f(x)=axex-1,g(x)=lnx+kx.
(1)求g(x)的單調(diào)區(qū)間;
(2)若k=1,f(x)≥g(x)恒成立,求實數(shù)a的取值范圍.
解(1)略.
(2)當(dāng)k=1 時,f(x)≥g(x) 恒成立,即axex-1≥lnx+x恒成立,由于x>0,故a≥令h(x)=則h′(x)=令p(x)=lnx+x,顯然p(x) 遞增,又p(1)=1>0,=-1<0,故存在惟一的使p(x0)=0 且當(dāng)x∈(0,x0)時,p(x)<0,h′(x)>0;當(dāng)x∈(x0,+∞)時,p(x)>0,h′(x)<0.
故hmax(x)=h(x0)=由于p(x0)=lnx0+x0=0,即x0=e-x0,從而hmax(x)=h(x0)=所求實數(shù)a的取值范圍為a≥1.
點(diǎn)評本題是一道精妙設(shè)計的好題,函數(shù)h(x)在x0處取得最大值,雖然x0無法直接求出,但是利用lnx0+x0=0代換后可以求出h(x0)的具體值.零點(diǎn)的設(shè)而不求是解決此類問題的一個重要方法,它就是針對導(dǎo)函數(shù)有零點(diǎn)且零點(diǎn)難以求出的情況,解題時有時還需要借助零點(diǎn)定理確定零點(diǎn)的范圍才能求解.
策略三:利用不等式局部放縮
例3若不等式xe2x-lnx-ax≥1 恒成立,求實數(shù)a的取值范圍.
解不等式xe2x-lnx-ax≥1 恒成立,分離參數(shù)得:a≤由 于ex≥x+1,故xe2x=e2x+lnx≥2x+lnx+1,于是≥=2,等號當(dāng)且僅當(dāng)2x+lnx=0時成立,顯然有唯一的實數(shù)x0滿足該方程.因此所求a的取值范圍為a≤2.
點(diǎn)評本題也可用和例2 一樣的虛設(shè)零點(diǎn)設(shè)而不求的方法求解.
例4當(dāng)x>1 時,不等式(x+1)lnx-a(x-1)>0 恒成立,求實數(shù)a的取值范圍.
解不等式(x+1)lnx-a(x-1)>0 恒成立,分離參數(shù)得:由于故等號當(dāng)且僅當(dāng)x=1 時成立,因此所求a的取值范圍為a≤2.
點(diǎn)評a<f(x)恒成立,則a<fmin(x).為求f(x)的最小值,我們可以適當(dāng)放縮,若能得到f(x)≥g(x)≥m,并且等號同時成立,則fmin(x)=m.
例5證明:當(dāng)x∈(0,1)∪(1,+∞)時,ex->0.
證明由于故構(gòu)造函數(shù)要證原不等式,只需證:即證當(dāng)x>1 時,lnx>成立;當(dāng)0<x<1時,lnx<成立.令f(x)=lnx-則故f(x)遞增,又f(1)=0,可見所證成立.
點(diǎn)評本題也可以采用切線放縮:易求得函數(shù)和函數(shù)g(x)=在x=1 處的切線分別為和從而有一般,對于指數(shù)函數(shù),我們常用的放縮有:ex≥x+1?ex-1≥x?ex≥ex,
策略四:根據(jù)函數(shù)的結(jié)構(gòu)特征,構(gòu)造同構(gòu)式
例6若對任意x>0,a(eax+1)≥恒成立,求實數(shù)a的取值范圍.
解不等式a(eax+1)≥兩邊同乘 以x得:ax(eax+1)≥2(x2+1lnx,進(jìn)一步有(eax+1)lneax≥(x2+1)lnx2.令f(x)=(x+1)lnx,則原不等式等價于:f(eax)≥f(x2).又易知f(x)在(0,+∞)上遞增,故eax≥x2,取對數(shù)分離參數(shù)可得:令易知g(x)在(0,e)上遞增,在(e,+∞)上遞減,故a≥2·gmax(x)=
點(diǎn)評當(dāng)函數(shù)f(x)的表達(dá)式比較復(fù)雜時,我們可以對其進(jìn)行等價變換,比如換元法,同構(gòu)法等,使得問題達(dá)到簡化的目的!
例7當(dāng)x>0 時,(ex-1)ln(x+1)>x2.
證明

令f(x)=所證為f(ex-1)<f(x).又當(dāng)x>0時,ex-1>x,故只需證f(x) 在(0,+∞) 上遞減.因為f′(x)=而故f′(x)<0.
點(diǎn)評本題也可采用ex>1+x+放縮來證明.
一般地,常見的同構(gòu)類型有:
類型1aea≤blnb,它可以從以下三個角度同構(gòu):
(1)改寫左邊:ealnea≤blnb,構(gòu)造函數(shù)f(x)=xlnx;
(2)改寫右邊:aea≤(lnb)elnb,構(gòu)造函數(shù)f(x)=xex;
(3)取對數(shù):a+lna≤lnb+ln(lnb),構(gòu)造函數(shù)f(x)=x+lnx.
類型2它可以從以下三個角度同構(gòu):
(3)取對數(shù):a-lna<lnb-ln(lnb),構(gòu)造函數(shù)f(x)=x-lnx.
類型3ea±a>b±lnb,它可以從以下兩個角度同構(gòu):
(1)改寫右邊:ea ±a>elnb ±lnb,構(gòu)造函數(shù)f(x)=ex±x;
(2)改寫左邊:ea ±lnea>b±lnb,構(gòu)造函數(shù)f(x)=x±lnx.
類型4拼湊后再同構(gòu):
(1)aeαx>lnx?axeax>xlnx,轉(zhuǎn)化為類型1;
(2)a(eax+1)≥?ax(eax+1)≥轉(zhuǎn)化為類型1.
策略五:指數(shù)對數(shù)分離,直線隔離
例8(2014 高考新課標(biāo)卷) 證明:當(dāng)x>0 時,
證明令f(x)=exlnx+從而所證f(x)>1等價于xlnx>設(shè)函數(shù)g(x)=xlnx,則g′(x)=1+lnx.所以當(dāng)x∈時,g′(x)<0;當(dāng)x∈時,g′(x)>0.故g(x)在上單調(diào)遞減,在上單調(diào)遞增,從而g(x)在(0,+∞)上的最小值為
設(shè)函數(shù)h(x)=則h′(x)=e-x(1-x).所以當(dāng)x∈(0,1) 時,h′(x)>0;當(dāng)x∈(1,+∞) 時h′(x)<0.故h(x)在(0,1)上單調(diào)遞增,在(1,+∞)上單調(diào)遞減,從而h(x)在(0,+∞)上的最大值為h(1)=綜上,當(dāng)x>0時,g(x)>h(x),即f(x)>1.
點(diǎn)評通過變形后求轉(zhuǎn)化為:f(x)>g(x),通過常數(shù)隔離后轉(zhuǎn)化為fmin(x)>gmax(x).
例9(2013年高考全國卷)設(shè)函數(shù)f(x)=ex-ln(x+m),當(dāng)m≤2 時,證明f(x)>0.
證明函數(shù)y=ex在x=0 處的切線方程為y=x+1,從而有ex≥x+1,等號當(dāng)且僅當(dāng)x=0 時成立;而函數(shù)y=ln(x+m)在x=1-m處的切線方程為y=x+m-1,函數(shù)y=ln(x+m)為凸函數(shù),從而ln(x+m)≤x+m-1,等號當(dāng)且僅當(dāng)x=1-m時成立;因為m≤2,故ln(x+m)≤x+m-1≤x+1≤ex,又等號不同時成立,從而ln(x+m)<ex.
點(diǎn)評這里我們采用切線隔離的方式,本題也可以采用虛設(shè)零點(diǎn)設(shè)而不求的方法求解.
策略六:利用端點(diǎn)效應(yīng)
例10(2016年高考四川卷)設(shè)函數(shù)f(x)=ax2-a-lnx,其中a ∈R.
(1)討論f(x)的單調(diào)性;
(2)確定a的所有可能取值,使得在區(qū)間(1,+∞)內(nèi)恒成立(e=2.718···為自然對數(shù)的底數(shù))
解(1)略.
g(x)=注意到g(1)=0,故可得
另一方面,當(dāng)a≥時,
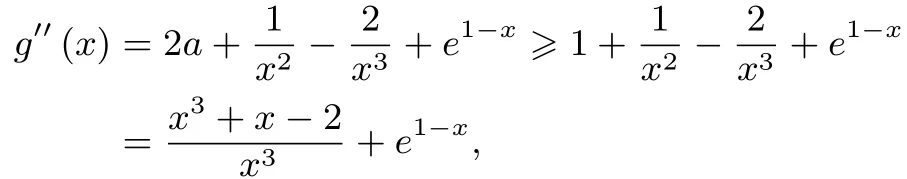
所以x∈(1,+∞),故x3+x-2>0,e1-x>0,于是g′′(x)>0.所以當(dāng)a≥時,g′(x) 在x∈(1,+∞) 單調(diào)遞增.所以g′(x)>g′(1)=2a-1≥0,故g(x) 在x∈(1,+∞)單調(diào)遞增.所以g(x)>g(1)=0,即g(x)在(1,+∞)上恒大于0.綜上,
以上是解決含有指數(shù)和對數(shù)的函數(shù)不等式問題的求解策略,具體求解時,我們需要仔細(xì)觀察函數(shù)的特征,從以上角度去多方面嘗試,采取合理的策略.
——以指數(shù)、對數(shù)函數(shù)同構(gòu)問題為例

