安徽省無為縣牛埠中學(238351) 朱小扣

例說不等式的幾種證明方法

安徽省無為縣牛埠中學(238351) 朱小扣

對不等式的考察一直是高考和競賽的熱點,不等式的證明方法也有很多,大多數(shù)同學經(jīng)常會覺得難以掌握.為此,本文將從幾個簡單的例子出發(fā),闡述解不等式的幾種方法,以期給初學者有所幫助,不對之處,歡迎指正.

方法二(赫爾德不等式)

證：由赫爾德不等式可得：

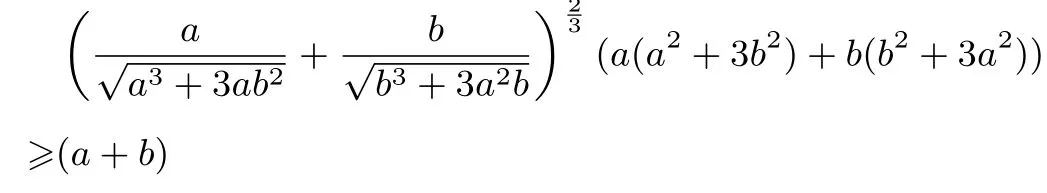
所以

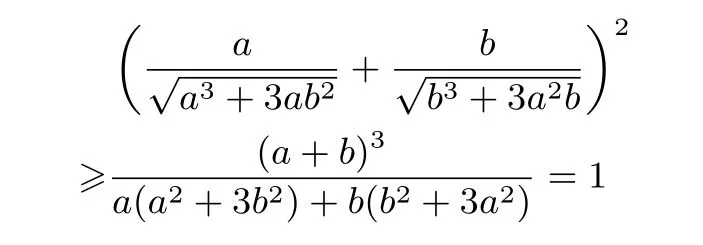
即證.

方法三(待定系數(shù)法)

分析嘗試找到一個r,使得：成立,故只需.依條件可知原不等等號成立時,a=b.為了找出r,可先令b=1得：.再令：.求導：

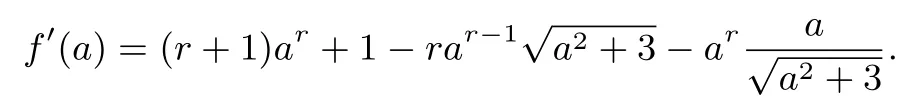
證

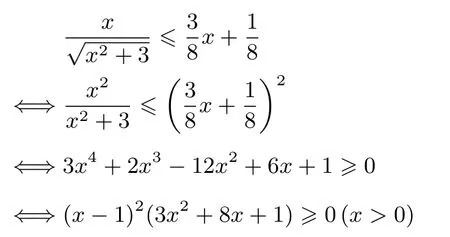
故

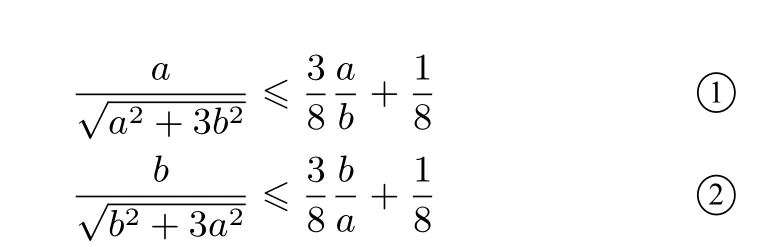
①+②即證.

用切線法還可以證明2015年高中數(shù)學聯(lián)賽安徽省初賽第9題：

解題思路(切線法)證即可.(注：在處的切線方程是y=2-x)

有時除了用切線法外還可以用割線法：

例三已知 a,b,c∈ R+,a+b+c=1,求證：.

方法五(割線法)可知在兩點的割線方程是,故只需證在(0,1)上恒成立即可.

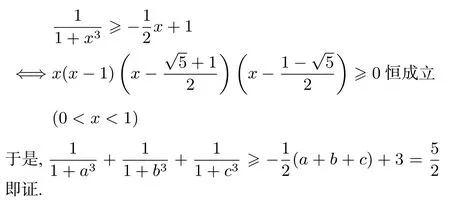
割線法還可以證明如下例題：

解題思路(割線法)只需證≤1+a ??a(3a+2)(a-1)≤0(0≤a≤1)(注：f(x)=在 (0,1),(1,2)兩點的割線方程是y=x+1)

上面闡述了證明不等式的五種方法,除此之外還有像柯西不等式,貝努利不等式等多種方法,證明方式也是千變?nèi)f化,本文只是闡述最基礎的方法.事實上,不管數(shù)學題目怎樣變化,但只要我們掌握其本質(zhì),就能一招制敵,學生必須具有一題多解,多題一解的能力,這樣才能在做題時,多角度,多思維的去考慮,才能在做題中達到自身水平的提高!希望本文能對初學者有所幫助.

[1]韓京俊.初等不等式的證明方法[M].哈爾濱工業(yè)大學出版社, 2014,2.