涂喆研 王文亮

(1陜西師范大學(xué)化學(xué)化工學(xué)院,陜西省大分子科學(xué)重點(diǎn)實(shí)驗(yàn)室,西安710062;2西安工程大學(xué)理學(xué)院,西安710048)

含自旋軌道角動(dòng)量耦合的耦合簇理論研究Zn2和Cd2二聚物的結(jié)構(gòu)和光譜常數(shù)

涂喆研1,2,*王文亮1

(1陜西師范大學(xué)化學(xué)化工學(xué)院,陜西省大分子科學(xué)重點(diǎn)實(shí)驗(yàn)室,西安710062;2西安工程大學(xué)理學(xué)院,西安710048)

在二分量相對(duì)論有效勢(shì)和與之匹配的基組aug-cc-pv n z-pp(n=Q,5)的基礎(chǔ)上,結(jié)合電子相關(guān)能的完備基組外推和四階多項(xiàng)式擬合,我們用含自旋軌道角動(dòng)量耦合的耦合簇方法研究了Zn2和Cd2的結(jié)構(gòu)和光譜常數(shù).盡管Zn2和Cd2的自旋軌道角動(dòng)量耦合效應(yīng)不及Hg2的明顯,但還是把自旋軌道角動(dòng)量耦合放在耦合簇迭代計(jì)算中,以獲得更加合理的理論結(jié)果.通過比較,理論結(jié)果與最新發(fā)表的實(shí)驗(yàn)結(jié)果或其他課題組的理論結(jié)果吻合得較好,因此我們的理論計(jì)算將有助于豐富對(duì)Zn2和Cd2光譜性質(zhì)的認(rèn)識(shí).

光譜常數(shù);自旋軌道角動(dòng)量耦合;二聚物;耦合簇方法

1 In troduction

Both relativistic effects and electron correlation are critical to provide reliable theoreticalestimates for propertiesofmolecules containing heavy elements.1Coupled-cluster theory has been shown to providean efficientand accurate treatmentof electron correlation.2One of themostpopularmethods nowadays to treat relativistic effects in an approximatemanner is the use of relativistic effective core potentials(ECPs).The interaction of core electronsw ith the valence electrons is replaced by an effective potentialand the core electrons are not longer treated explicitly. Furthermore,when spin-orbitcoupling isneglected,it isstraightforward to implementscalar relativistic ECPs in the framework ofnon-relativistic calculations since relativity isaccounted for only through the parametersof the ECPs.However,spin-orbitcoupling has a visible influence on the properties of heavy-element coumpouds.3Spin-orbitcoupling can also be included using ECPs and such treatments result in two componentapproachesw ith the additional advantage that the spin-orbitoperator can be represented as a one-electron operator4which can reduce the computational costverymuch.

A both efficientand high-precision treatment of spin-orbit coupling based on two componentECPs is to consider the spinorbit coupling only at coupled cluster level.By including spinorbit coupling only in the electron correlation part,the Hartree-Fock partand the integral transformationwillbeexactly the same as in nonrelativistic or scalar relativistic calculations.4It isworthy tomention thatcoupled cluster theory isable to account formost of the orbital relaxation effects via single excitations in the cluster operator.5The advantage of putting the spin-orbit coupling in the postHartree-Fock part is that themolecularorbitals(MOs)aswell as the two-electron integrals in theMO representation remain real and can be classified according to the irreducible representation of themolecular single pointgroup.4This issue can be explored to reduce the computational effort significantly w ith respect to fully relativistic four component coupled cluster calculations. Therefore,two component ECPs based coupled-cluster theory w ith spin-orbitcoupling isused to study Zn2and Cd2in thiswork.

Diatomicmolecule formed from two closed shellatoms is van derWaalsmolecule,Zn2and Cd2should belong to this category though some authors think that they are notpure van derWaals molecules.6-8Theground statesof Zn2and Cd2areweakly bounded w ith a large equilibrium distances.

Experimentally,Zn2and Cd2are lessextensively studied than Hg2due to theirhigher vaporization temperatures.9,10Though recent laser spectroscopies of Zn2and Cd2seem to give reliable values of harmonic frequency(ωe)and dissociation energy(De)of theelectronic ground states,the equilibrium distances(Re)of Zn2and Cd2are less certain.10

Theoretically,statement such as“the full consistency w ith spectroscopic constants com ing from experimenthas been given up because of the computational demands”appeared in a relativistic calculation paper.11In recent three years,we find“accurate potentialenergy curves”calculatedwith relativistic effects,which considerably narrowed the gapsbetween theory and experiment,12but the discrepancies still remain.It isworthy tomention that Li etal.10provided the latest theoretical results,but their results relied on potential functionalw ithmany parameters.

Most researchers think that the spin-orbitcoupling effectsof Zn and Cd elements are small13-16and the perturbationmethod is exact enough to treat the spin-orbit coupling effect of Zn2and Cd2.17-19However,if accurate valuesof spectroscopic constantsare wanted,one would better use iterativemethod instead of perturbation method to treat spin-orbit coupling.In fact,Kullie has already used a relativistic four-component Dirac-Coulomb Ham iltonian w ith spin-orbitcoupling in the framework of timedependent density functional theory and linear response approximation to calculate the electronic state of Zn220and Cd2.21However,it is w idely known that the results of spectroscopic constants are very dependent of the choice of functional.The more generaland high-precision ab initio calculations are desired and w illbe helpful to understand the spectral character of these two dimers.

2 Basic equations

The nonrelativistic one-component CCSD(coupled-cluster approachw ith singlesand doubles level)energy equation is then4and the amplitude equationsare22

w ith the F and W intermediates defined as

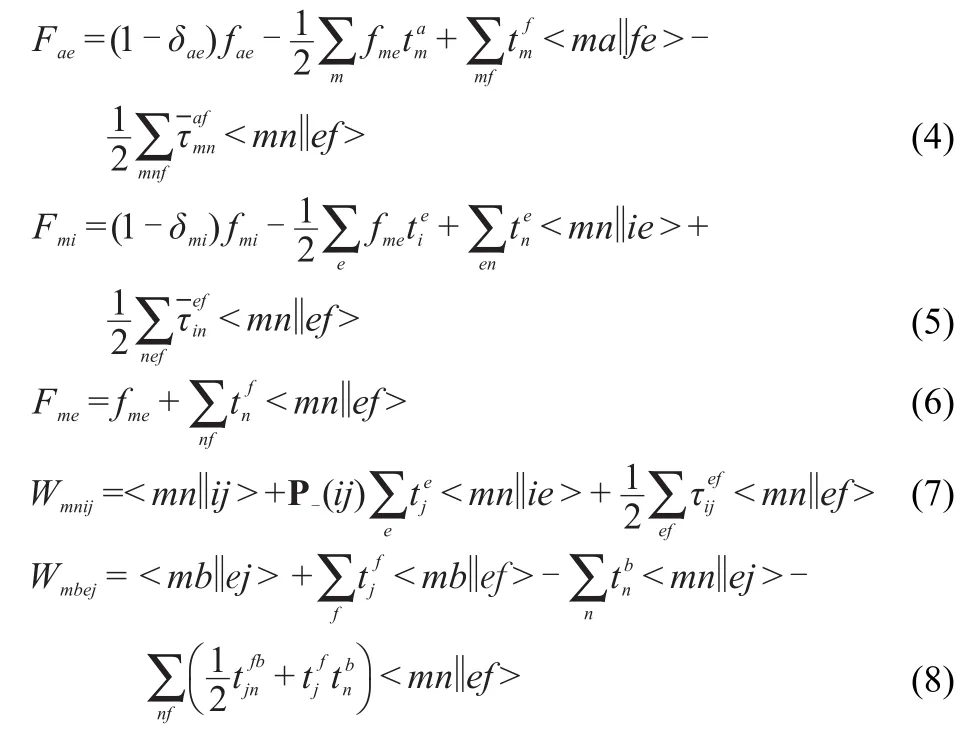
theτamplitudesare defined as

the permutation operator P-isgiven by

and theorbitalenergy denominatorsare defined as

The two-componentCCSD equationsare exactly the same as theabove nonrelativistic one component counterpartsexcept that the Fockmatrix has contributions from the spin-orbitcoupling due to the use of two-componentECPs.

Thus,in the above equations,EHFis the scalar relativisticHartree-Fock energy w ithoutspin-obitcoupling,i,j,k,…are the indices for occupied spin orbits,a,b,c,…denote virtue spin orbits,and p,q,r,…are for general spin orbits,fpqis the Fock matrix elementw ith the contribution of spin-orbit coupling included.The Fockmatrix elements can bew ritten as

where F0is the Fock operatorwithoutspin-orbitcoupling and hSOCis the spin-orbit coupling operator which is reduced to oneelectron operator due to the use of two-componentECPs.4

Furthermore,consideration of triple excitationshasbeen shown to be important in order to achieve highly accurate results in coupled cluster calculations.23The most popular noniteration scheme to account for triple excitations is the CCSD(T)approach.24Theenergy correction due to tripleexcitation correction is then given by25

w ith the cyclic permutation operator

Itshould be pointed out that the occupied-virtue block of the Fockmatrix in the second term on the righthand side of Eq.(13) solely comes from spin-orbit coupling.Spin-orbit coupling thus contributes directly to the triple excitation.With respect to the other denominators in Eqs.(1-16),one can find the details in the corresponding literature.

3 Com pu tationaldetails

CFOUR is a program package for perform ing high-level quantum chemical calculations on atoms and molecules.26Our coupled cluster calculations in thiswork are performed in CFOUR package.Both CCSD(T)w ithout spin-orbit coup ling and CCSD(T)including spin-orbit coupling(SOC-CCSD(T))27methodsare used to calculate the energiesof atomsaswellas9 single pointenergies of around equilibrium position of these two dimers.The intervalof the 9 points isdefined to be 0.005 nm.The two-componentECPs,ECP10MDF,andmatched basissets,augccpv n z-pp(n=Q,5)28,are used in the calculations.The electron correlation energies from CCSD(T)and SOC-CCSD(T)are extrapolated to the results of completed basis set(CBS).The formula of CBS forelectron correlation energy can bew ritten as

In theabove equation,n is the same to the n in thebasisset,the valueof n can bedefined to be4,5 in thiswork;represents the calculated electronic correlation energies from aug-ccpv n z-pp basis sets;the values of c andcan be obtained through solving equation sets in Mathematica software package.The Hartree-Fock limit is taken from theaug-ccpv5z-pp basisset.The basis setsuperposition error(BSSE)isnotcorrected in thiswork because of the use of high level basis sets.And the four order polynomial fitting technique isused to calculate the bond lengths and spectroscopic constantsof these two dimersand the related fitting formula can be found in the reference29and references therein.

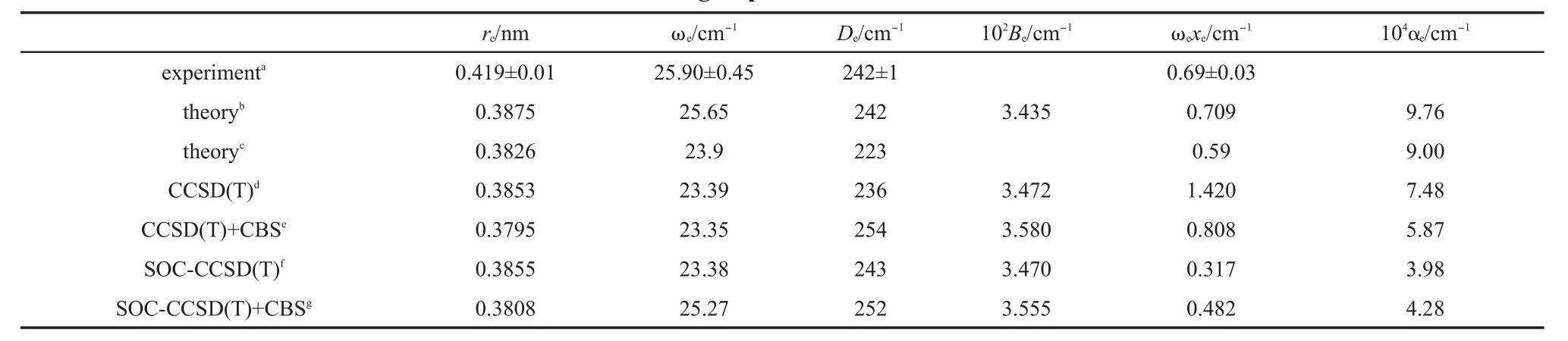
Table1 Calculated bond lengthsand spectroscopic constantsof Zn2com pared to the latestexperimental and other group's theoretical resu lts

4 Resu lts and d iscussion

4.1Zn2

The calculated bond lengthsand spectroscopic constants,the latestexperimental resultsand othergroup's theoretical results9,10,12are listed in Table 1.For thebond length,our result from CBS+SOCCCSD(T)is closest to the result from Pahl etal.12In Pahl etal.'s work,the spin-orbitcontributionwasobtained from Dirac-Fock calculations and the spin-orbitenergieswere then added to the scalarenergies.For Zn2whose spin-orbitcoupling effectisweakest, both Pahl etal.'s calculated method and our present calculated method are reasonable.With respect to Li etal.'s theoretical results,though theoptimized potential function isused to determine the structure and spectroscopic constants,the obtained bond length isabit longer than Pahl etal.'sand oursbond length,much shorter than theexperimentalvalue.9Perhaps,becauseof themultireference character in Zn2,both Pahl etal.'sand ours ab initio's resultsare smaller than the experimental value.9In otherwords,the noniterative triple excitation in single-reference coupledcluster procedure may not fully describe the multi-reference characterof Zn2.On the otherhand,from our calculated valuesof bond length,asone can expect,the spin-orbitcoupling effectdoes notchange bond length toomuch,about just0.001 nm.Forother spectroscopic constants in Table1,all the theoretical resultsagree with the corresponding experimental resultsverywell.Though the experimental rotational constantand vibrational-rotational coupling constantareabsent,all the theoreticalvaluesagreew ith each other verywell.

Table2 Calcu lated bond lengthsand spectroscopic constantsof Cd2compared to the latest experim entaland other group's theoretical resu lts

4.2Cd2

The calculated bond lengthsand spectroscopic constants,the latest experimental results,and other group's theoretical results10,12,30for Cd2are listed in Table 2.For the bond length,our result from CBS+SOC-CCSD(T)is closest to the experimental result.The theoreticalbond length from Pahl etal.'swork isabit longer than the experimental value.The treatmentof spin-orbit coupling in Pahl etal.'sworkmentioned abovemay notbe the mostsuitable approach for Cd2whose spin-orbit coupling effect ismore visible than Zn2.With respect to Li et al.'s theoretical results,though theoptimized potential function isused to determine the structure and spectroscopic constants,the obtained bond length ismuch longer than the experimentalvalue.On the other hand,from our calculated values of bond length,the spin-orbit coupling effectmakes the bond length abitshorter,about0.002 nm.For other spectroscopic constants in Table 2,all the theoretical results agreew ith the corresponding experimental results very well.Though the experimental rotational constant and vibrational-rotational coupling constant are absent,all the theoreticalvaluesagreew ith each other very well.

5 Summ ary

In thiswork,the two-component coupled-cluster theory w ith spin-orbit coupling,the completed basis setsextrapolation,and the four-order polynomial fitting technique are used to study the structuresand spectroscopic constantsof Zn2and Cd2.The results from CBS+SOC-CCSD(T)calculations are themost reliable values in comparisonw ith the latestexperimentalorothergroup's theoretical results.The spin-orbitcouplingmainly affects thebond length of Cd2,and other valuesare almostnotaffected by spinorbit coupling.Our theoretical resultsw ill be helpful to understand the spectral characterof these two dimersand CBS+SOCCCSD(T)method is suitable for studying the electronic structures of these van derWaalsdimers containing heavy elements.

With respect to Hg2whose spin-orbitcoupling ismostvisible, the results of Hg2w ill be reported in the near future due to its complexity.

(1)Pyykko,P.Chem.Rev.1988,88,563.doi:10.1021/cr00085a006

(2)Bartlett,R.J.;Musial,M.Rev.Mod.Phys.2007,79,291.doi: 10.1103/RevModPhys.79.291

(3)Liu,W.;VanWullen,C.J.Chem.Phys.1999,110,3730.doi: 10.1063/1.478237

(4)Wang,F.;Gauss,J.;vanWullen,C.J.Chem.Phys.2008,129, 064113.doi:10.1063/1.2968136

(5)Christiansen,O.;Hattig,C.;Gauss,J.J.Chem.Phys.1998,109, 4745.doi:10.1063/1.477086

(6)Yu,M.;Dolg,M.Chemical Physics Letters1997,273,329.doi: 10.1016/S0009-2614(97)00609-X

(7)Schautz,F.;Flad,H.J.;Dolg,M.TheoreticalChemistry Accounts1998,99,231.doi:10.1007/s002140050331

(8)Strojecki,M.;Ruszczak,M.;?ukomski,M.;Koperski,J. ChemicalPhysics2007,340,171.doi:10.1016/j. chemphys.2007.08.016

(9)Strojecki,M.;Ruszczak,M.;Kro?nicki,M.;?ukomski,M.; Koperski,J.Chemical Physics2006,327,229.doi:10.1016/j. chemphys.2006.04.008

(10)Wei,L.M.;Li,P.;Qiao,L.W.;Tang,K.T.J.Chem.Phys.2013, 139,154306.doi:10.1063/1.4824889

(11)Bucinsky,L.;Biskupic,S.;Ilcin,M.;Lukes,V.;Laurinc,V. JournalofComputationalChemistry 2009,30,65.doi:10.1002/ jcc.v30:1

(12)Pahl,E.;Figgen,D.;Borschevsky,A.;Peterson,K.A.; Schwerdtfeger,P.TheoreticalChemistry Accounts2011,129, 651.doi:10.1007/s00214-011-0912-1

(13)Bera,N.C.;Das,A.K.Chemical Physics Letters2007,437,257.doi:10.1016/j.cplett.2007.02.010

(14)Bender,C.F.;Rescigno,T.N.;Schaefer,H.F.,III;Orel,A.E. J.Chem.Phys.1979,71,1122.doi:10.1063/1.438456

(15)Takewaki,H.;Tomonari,M.;Nakamura,T.J.Chem.Phys. 1985,82,5608.doi:10.1063/1.448596

(16)Czuchaj,E.;Rebentrost,F.;Stoll,H.;Preuss,H.Chemical Physics Letters1996,255,203.doi:10.1016/0009-2614(96) 00336-3

(17)Ellingsen,K.;Saue,T.;Pouchan,C.;Gropen,O.Chemical Physics2005,311,35.doi:10.1016/j.chemphys.2004.09.038

(18)Hay,P.J.;Dunning,T.H.,Jr.;Raffenetti,R.C.J.Chem.Phys. 1976,65,2679.doi:10.1063/1.433411

(19)Figgen,D.;Rauhut,G.;Dolg,M.;Stoll,H.Chemical Physics 2005,311,227.doi:10.1016/j.chemphys.2004.10.005

(20)Kullie,O.JournalofAtomic,Molecular,and OpticalPhysics 2012,2012,361974.doi:10.1155/2012/361947

(21)Kullie,O.Chemical Physics2013,415,112.doi:10.1016/j. chemphys.2012.12.020

(22)Stanton,J.F.;Gauss,J.;Watts,J.D.;Bartlett,R.J.J.Chem. Phys.1991,94,4334.doi:10.1063/1.460620

(23)Kucharski,S.A.;Bartlett,R.J.J.Chem.Phys.1992,97, 4282.doi:10.1063/1.463930

(24)Raghavachari,K.;Trucks,G.W.;Pople,J.A.;Head-Gordon,M. Chemical Physics Letters1989,157,479.doi:10.1016/S0009-2614(89)87395-6

(25)Watts,J.D.;Gauss,J.;Bartlett,R.J.J.Chem.Phys.1993,98, 8718.doi:10.1063/1.464480

(26)CFOUR,aquantum chem icalprogram packagew ritten by Stanton,J.F.;Gauss,J.;Harding,M.E.;Szalay,P.G.w ith contributions from Auer,A.A.;Bartlett,R.J.;Benedikt,U.; Berger,C.;Bernholdt,D.E.;Bomble,Y.J.;Cheng,L.; Christiansen,O.;Heckert,M.;Heun,O.;Huber,C.;Jagau,T. C.;Jonsson,D.;Jusélius,J.;K lein,K.;Lauderdale,W.J.; Matthews,D.A.;Metzroth,T.;Mück,L.A.;O'Neill,D.P.; Price,D.R.;Prochnow,E.;Puzzarini,C.;Ruud,K.; Schiffmann,F.;Schwalbach,W.;Simmons,C.;Stopkow icz,S.; Tajti,A.;Vázquez,J.;Wang,F.;Watts,J.D.and the integral packages MOLECULE(A lm l?f,J.;Taylor,P.R.),PROPS (Taylor,P.R.),ABACUS(Helgaker,T.;Jensen,H.J.A.; J?rgensen,P.;Olsen,J.),and ECP routinesby M itin,A.V.;van Wüllen,C.For the currentversion,seehttp://www.cfour.de.

(27)Tu,Z.Y.;Yang,D.D.;Wang,F.;Guo,J.W.J.Chem.Phys. 2011,135,034115.doi:10.1063/1.3611052

(28)Peterson,K.A.;Puzzarini,C.TheoreticalChemistry Accounts 2005,114,283.doi:10.1007/s00214-005-0681-9

(29)Yang,D.D.;Wang,F.TheoreticalChemistry Accounts2012, 131,1117.doi:10.1007/s00214-012-1117-y

(30)Strojecki,M.;Kro?nicki,M.;Zgoda,P.;Koperski,J.Chemical Physics Letters2010,489,20.doi:10.1016/j.cplett.2010.02.039

Coup led-Cluster Theo retical Study o f Struc tu res and Spec troscop ic Constan ts o f Dim ers Zn2and Cd2w ith Sp in-Orbit Coup ling

TU Zhe-Yan1,2,*WANGWen-Liang1
(1Key Laboratory forMacromolecular Science ofShaanxiProvince,SchoolofChemistry and Chemical Engineering,Shaanxi NormalUniversity,Xi'an 710062,P.R.China;2SchoolofScience,Xi'an Polytechnic University,Xi'an 710048,P.R.China)

The structures and spectroscopic constants of Zn2and Cd2were studied using the coup led-cluster theory w ith spin-orbitcoup ling based on the two-component relativistic effective core potentialandmatched basis sets aug-cc-pv n z-pp(n=Q,5),combining com p lete basis setextrapolation of the electronic correlation energy and fourth-order polynom ial fitting technique.Spin-orbitcoupling was included in the post-Hartree-Fock p rocedure,i.e.,in the coup led-cluster iteration,to obtainm ore reasonab le results,although the spin-orbit coup ling effectobserved in Zn2and Cd2is notvisible as it is in Hg2.Our theoretical results agree wellw ith the latestexperimentalvalues and othergroups'theoreticalresults,and willbe helpfulin understanding the spectral characteristics of these two dimers.

Spectroscopic constant;Spin-orbitcoup ling;Dimer;Coup led-cluster theory

O641

icle]

10.3866/PKU.WHXB201503261 www.whxb.pku.edu.cn

Received:November 14,2014;Revised:March 24,2015;Published onWeb:March 26,2015.

?Corresponding author.Email:tuzheyan@126.com;Tel:+86-18392679232.

The projectwassupported by the Start-up Fundsof Xi'an Polytechnic University,China(BS1211)and Scientific Research Program Funded by ShaanxiProvincial Education Department,China(2013JK0679).

西安工程大學(xué)博士科研啟動(dòng)基金(BS1211)和陜西省教育廳專項(xiàng)科研計(jì)劃項(xiàng)目(2013JK0679)資助

?Editorialoffice of Acta Physico-Chimica Sinica