Mohsen MOGHTADAEI Hassan SABERI NIK Saeid ABBASBANDY

1 Introduction

The electrohydrodynamic flow of a fluid in an ion drag configuration in a circular cylindrical conduit is governed by a nonlinear second-order ordinary differential equation.In[1],McKee et al.investigated the following boundary value problem:

subject to the boundary conditions

A fully developed laminar flow in the“ion-drag”configuration is displayed in Figure 1,where a circular cylindrical conduit of radius has an insulating wall supporting screens atz=0 andz=L.

Herew(r)is the fully-developed fluid velocity as a function of the radial distancerfrom the center of the cylindrical conduit.The radius of the tube has been scaled to one.His the Hartmann electric number and the nondimensional parameterαis a parameter related to the pressure gradient,the ion mobility,and the current density at the inlet of the conduit.

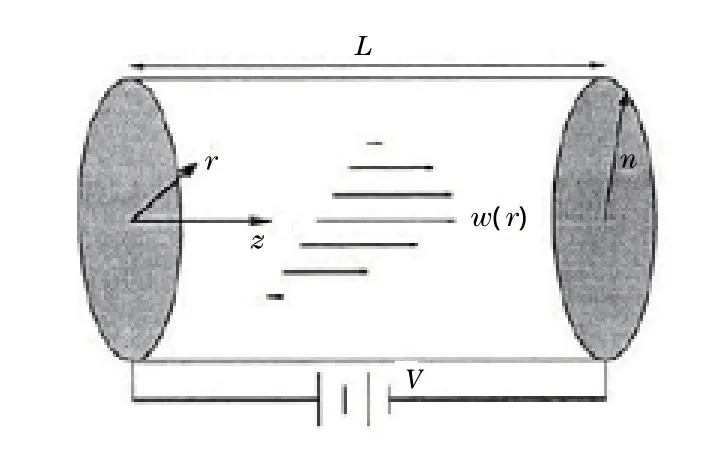
Figure 1 Ion-drag flow in a circular cylindrical conduit

Also,the degree of non-linearity in this equation is determined byαand the equation can be approximated by two different linear equations for very small or very large values ofαrespectively.In[1],the authors provide numerical solutions to(1.1)–(1.2)for various values ofHandαalong with perturbation solutions of the fluid velocities forα1 andα1.In[2],Paullet presented rigorous results concerning the existence and uniqueness of a solution to this BVP for all relevant values of the parameters.He also showed that the solution is monotonically decreasing and derived bounds on it in terms of the parameters.

Due to the mathematical complexity of nonlinear partial differential equations,different methods,such as the homotopy analysis method,the modified mapping method,the extended mapping method and numerical techniques,have been used for solving PDEs(see[3–6]).In 1992,Liao[7–10]employed the basic ideas of the homotopy in topology to propose a general analytic method for nonlinear problems,namely,the homotopy analysis method(HAM,for short).This method has been successfully applied to solve many types of nonlinear problems in science and engineering,such as the viscous flows of non-Newtonian fluids(see[11]),the KdV-type equations(see[12]),finance problems(see[13]),and so on.

The HAM contains a certain auxiliary parameter?which provides us with a simple way to adjust and control the convergence region and rate of convergence of the series solution.Moreover,by means of the so-called-curve,it is easy to determine the valid regions ofto gain a convergent series solution.The HAM,however,suffers from a number of restrictive measures,such as the requirement that the solution sought should conform to the so-called rule of solution expression and the rule of coefficient ergodicity.These HAM requirements are meant to ensure that the implementation of the method results in a series of differential equations which can be solved analytically.

In a recent study,Motsa et al.[14–17]proposed a spectral modification of the homotopy analysis method,i.e.,the spectral homotopy analysis method(SHAM for short)that seeks to remove some restrictive assumptions associated with the implementation of the standard homotopy analysis method.The SHAM approach imports some of the ideas of the HAM,such as the use of the convergence controlling auxiliary parameter.In the implementation of the SHAM,the sequence of the so-called“deformation”differential equations is converted into a matrix system by applying the Chebyshev pseudospectral method.Recently,Mastroberardino[18]applied the classical homotopy analysis method to solve the problem of(1.1).His computations showed that the HAM solutions are in excellent agreement with numerical solutions obtained with Matlab.

In order to overcome some of the limitations of the standard homotopy analysis method,in this paper,we apply the SHAM to solve the nonlinear boundary value problem for the electrohydrodynamic flow of a fluid in an ion drag configuration in a circular cylindrical conduit.The advantage of this approach is that it eliminates the restriction in the standard HAM of searching for prescribed solutions that conform to the rule of solution expression and the rule of coefficient ergodicity.We show that in using the SHAM,any form of initial guess may be used as long as it satisfies the boundary conditions whereas in HAM one is restricted to choosing an initial approximation that would make the integration of the higher-order deformation equations possible.In addition,we show that SHAM is more flexible than HAM as it allows for a wider range of linear operators and one is not restricted to using the method of higher-orderdifferential mapping.The range of admissiblehvalues is much wider in SHAM than in HAM.For the problem considered in this study,we show that the new approach leads to faster convergence in comparison with the standard HAM approach.

This paper has been organized as follows.In Section 2,the solution of the nonlinear boundary value problem for the electrohydrodynamic flow of a fluid in an ion drag configuration in a circular cylindrical conduit and a convergence analysis of the HAM are presented.In Section 3,we discuss the SHAM solution of the nonlinear boundary value problem.In Section 4,we summarize the main results obtained in this paper.Finally,the conclusion is given in Section 5.

2 Solution Methods

In this section,we give a brief description of the application of the standard homotopy analysis method for solving(1.1).Then,we will describe the new approach that uses the spectral homotopy analysis method for solving the governing nonlinear equation(1.1).

2.1 Solution by the homotopy analysis method

To solve the nonlinear ordinary differential equation(1.1),using the HAM we choose the initial approximation

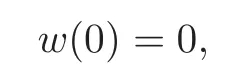
which satisfies the boundary conditions(1.2).Using the method of the highest-order differential matching,we consider an auxiliary linear operator of the form

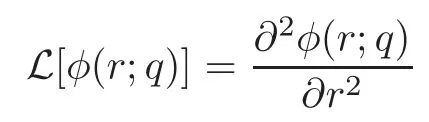
with the property

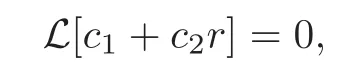
wherec1andc2are arbitrary integration constants.

Furthermore,the governing equation(1.1)suggests that we define the following nonlinear operator:

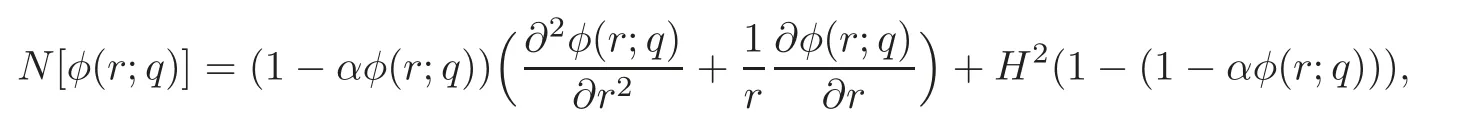
whereq∈[0,1]is an embedding parameter andφ(r;q)is an unknown function.Using the above definitions,we construct the so-called zero-order deformation equation as

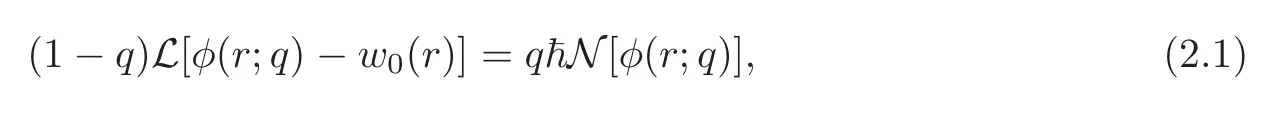
whereis a convergence controlling parameter,andw0(r)is an initial approximation.Obviously,whenq=0 andq=1,it holds that

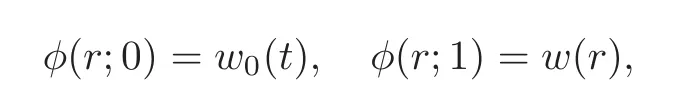
respectively.Thus,asqincreases from 0 to 1,the solutionsφ(r;q)vary from the initial guessesw0(r)to the solutionsw(r).Expandingφ(r;q)in the Taylor series with respect toq,we have

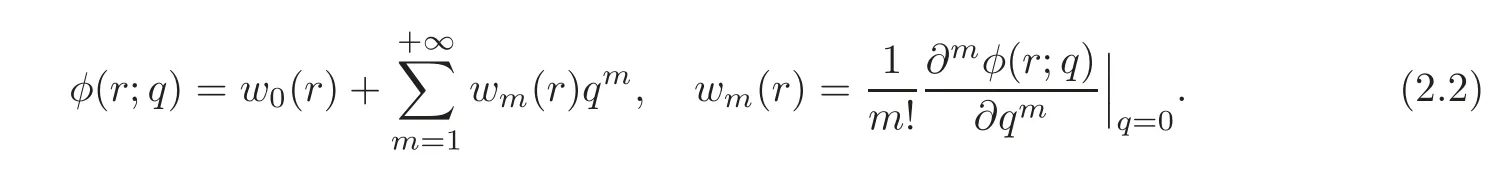
The convergence of the above series depends on the auxiliary parameter(see[19]).Assuming that the auxiliary parameteris carefully selected so that the above series is convergent whenq=1,we have,in view of(2.2),that

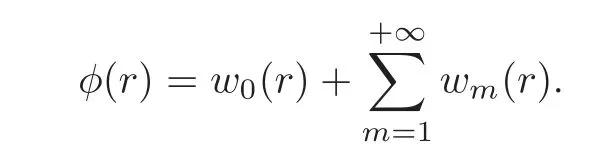
Using the ideas of the standard HAM approach(see[19]),we differentiate the zeroth-order equation(2.1)mtimes with respect toq,then setq=0 and finally divide the resulting equation bym!to obtain the following equation,which is referred to as them-th order(or higher order)deformation equation

with the boundary conditions

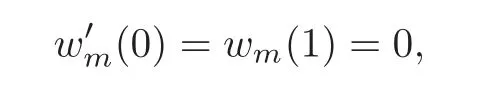
where

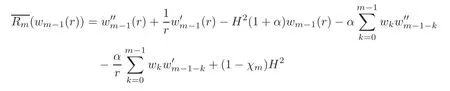
and

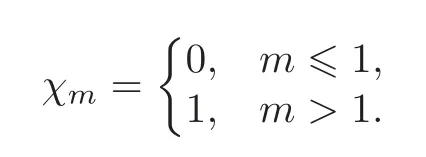
Them-th order deformation equations form a set of linear ordinary differential equations and can be easily solved,especially by means of the symbolic computation software,such as Matlab,Maple,Mathematica,and others.

2.2 A convergence analysis of the HAM

Let us consider the nonlinear boundary value problem(1.1)in the form of following functional equation:

whereFis a nonlinear operator.It is noted that HAM is equivalent to determining the sequence

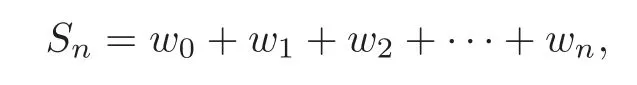
by using the iterative scheme

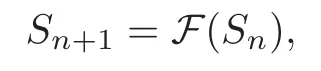
associated with the functional equation

Theorem 2.1Let F be an operator from a Hilbert space H into H and w(r)be theexact solution of(2.3).The series solutionconverges to w(r)when?0≤α<1,wk+1≤αwk,?k∈N∪{0}.

ProofWe show that,is a Cauchy sequence in the Hilbert spaceH.For this reason,consider

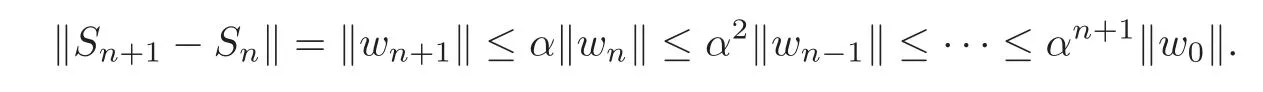
But for everyn,m∈N,n≥m,we have

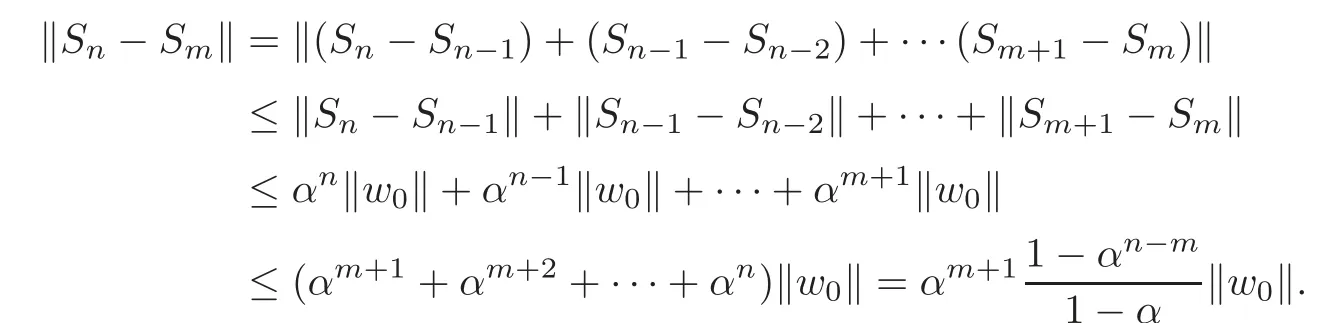
Since 0<α<1,we getis a Cauchy sequence in the Hilbert spaceH,and this implies that

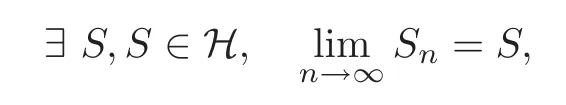
i.e.,converges.This completes the proof of Theorem 2.1.

But,solving(2.3)is equivalent to solving(2.4),and this implies that ifFis a continuous operator,then

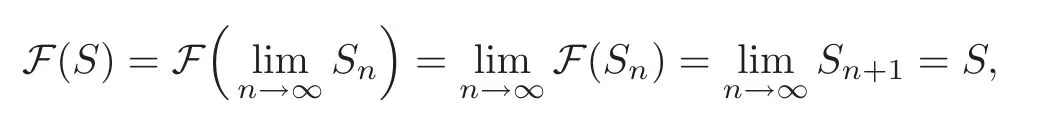
i.e.,Sis a solution of(2.3),too.

Definition 2.1For every k∈N∪{0},we define

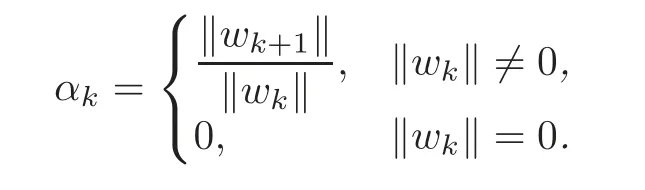
Corollary 2.1In Theorem2.1,wkconverges to w(r)when0≤αk<1,k=1,2,3,···.

Theorem 2.2If the series solution

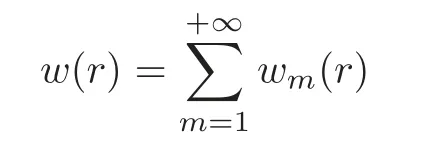
converges,then it is an exact solution of the nonlinear problem(2.3).

ProofWe assume that the series solution converges.So we have

and it holds that

We can verify that

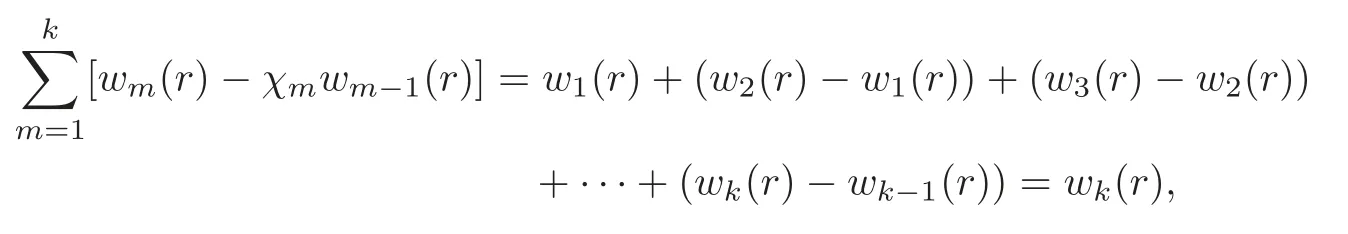
which gives us,according to(2.6),

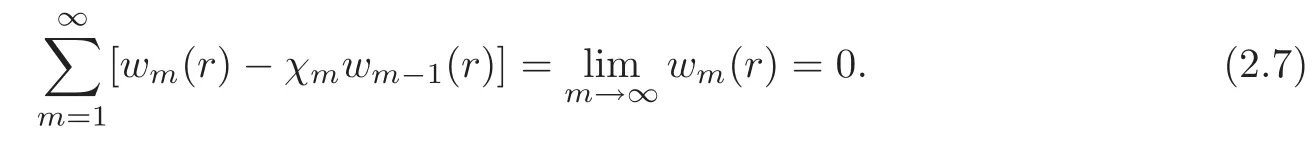
Furthermore,using(2.7)and the definition of the linear operatorL,we have

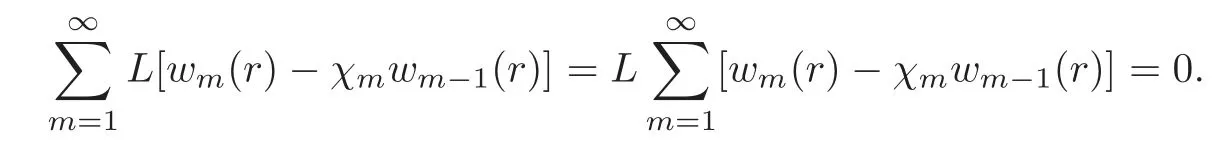
In this line,we can obtain that

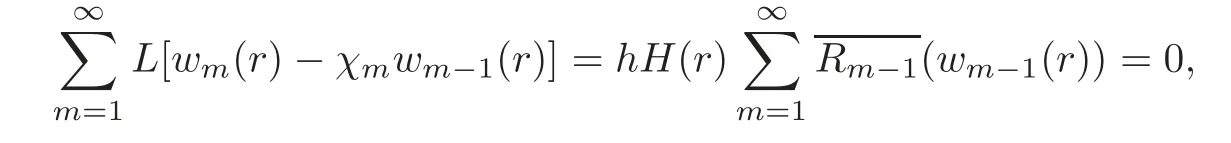
which gives,sinceh0 andH(r)0,that

Substitutingwm?1(r))into the above expression and simplifying it,we have

From(2.8)–(2.9),we have

On the other hand,in view of(1.2)and(2.5),it holds that

SoS(r)must be the exact solution of the nonlinear boundary value problem(1.1).This completes the proof of the theorem.

3 Spectral Homotopy Analysis Solution

In this section,we use the Chebyshev spectral collocation method to solve(1.1)–(1.2).We remark that before applying the spectral method,we use the transformationto map the region[a,b]to the interval[?1,1]on which the spectral method is defined.The advantage of this modification is that we get a technique that is more efficient and does not depend on the rule of solution expression and the rule of ergodicity,unlike the standard HAM.In addition,the range of admissiblevalues is much wider in the SHAM.Therefore,we begin by transforming the domain of the problem from[0,1]to[?1,1]using the mapping

It is also convenient to introduce the transformation

Substituting(3.1)in the governing equation and boundary conditions(1.1)–(1.2)gives

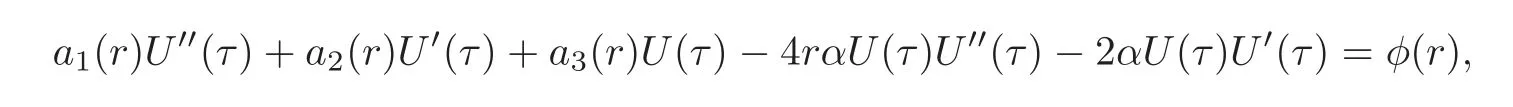
subject to

where the primes now denote differentiation with respect toτand

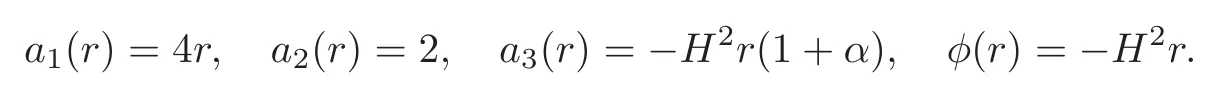
The initial approximation is taken to be the solution of the nonhomogeneous linear part of the governing equation(3.1)given by

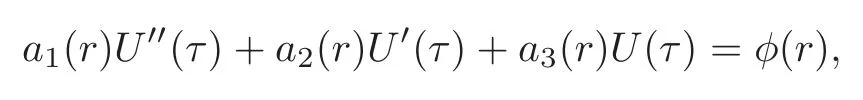
subject to

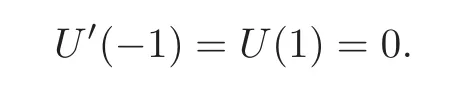
The unknown functionU0(τ)is approximated as a truncated series of Chebyshev polynomials of the form

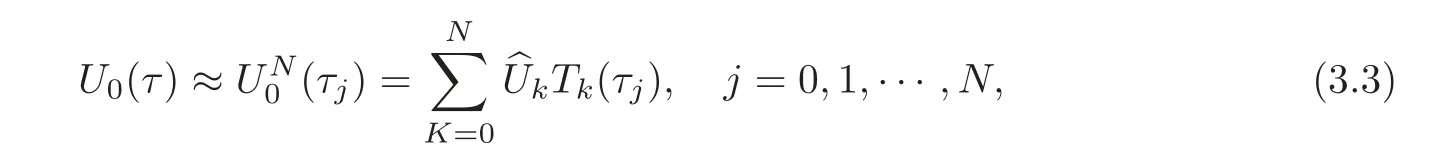
whereTkis thek-th Chebyshev polynomial,,are coefficients andτ0,τ1,···,τNare Gauss-Lobatto collocation points(see[20–21])defined by

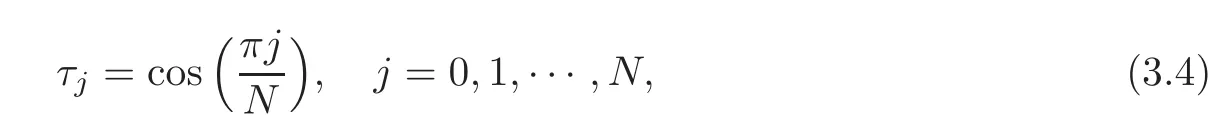
which are the extremes of theN-th order Chebyshev polynomial

The Chebyshev spectral differentiation matrixDis used to approximate the derivatives of the unknown variableswm(r)at the collocation points as the matrix vector product

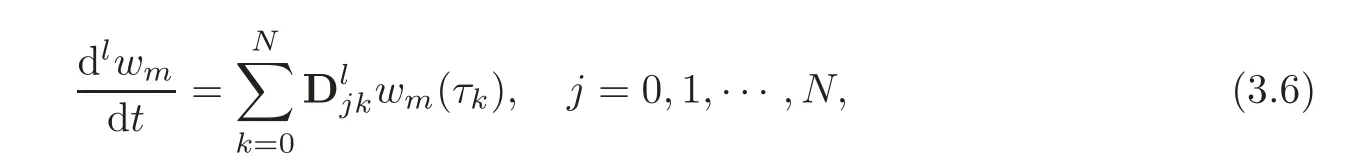
wherelis the order of differentiation andDis the Chebyshev spectral differentiation matrix whose entries are defined as(see[20–21])

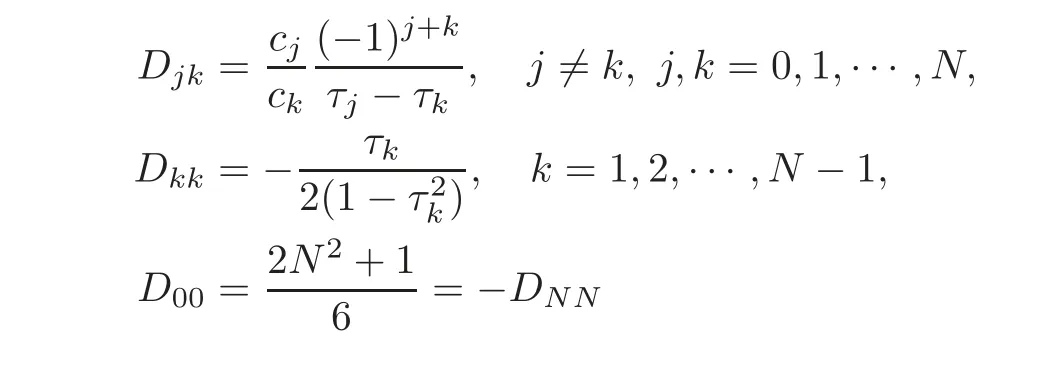
with

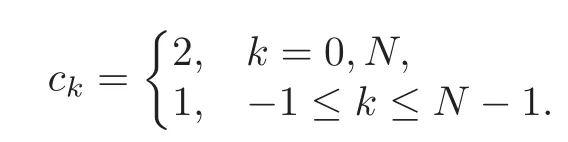
Substituting(3.3)–(3.6)into(3.1)–(3.2)yields

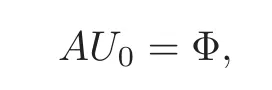
subject to the boundary conditions

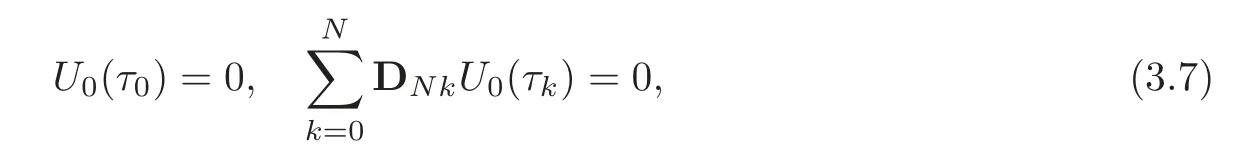
where

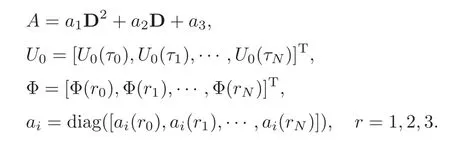
In the above definitions,the superscript T denotes the transpose,and diag is a diagonal matrix of size(N+1)×(N+1).

To implement the boundary conditions(3.7),we delete the first and last rows and columns ofA,as well as the first and last rows ofU0andU.The boundary condition(3.7)is imposed on the resulting last row of the modified matrixA,setting the resulting last row of the modified matrixUto be zero.The values of[U0(τ0),U0(τ1),···,U0(τN)]are then determined by the equation

which provides us with the initial approximation for the SHAM solution of the governing equation(3.1).

Now,we define the linear operator

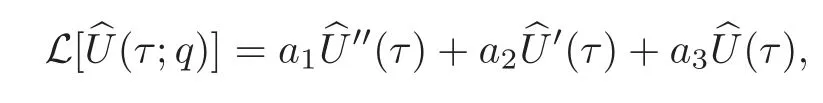
whereq∈[0,1]is the embedding parameter,and(τ;q)is an unknown function.The zeroth order deformation equation is given by

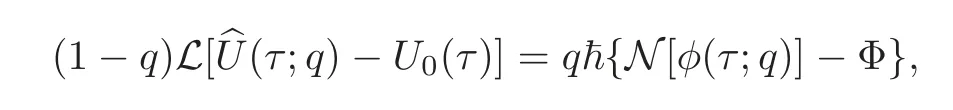
whereis a convergence controlling parameter,andNis a nonlinear operator given by

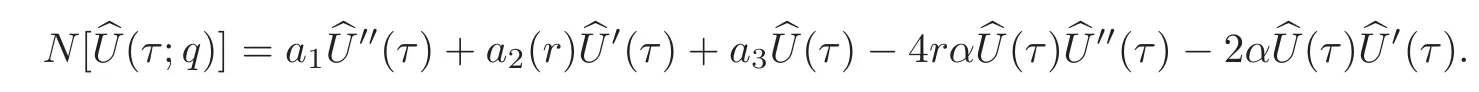
Them-th order deformation equations are

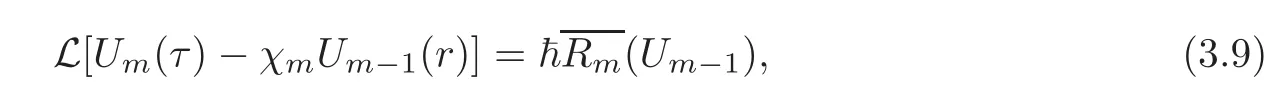
subject to the boundary conditions

where

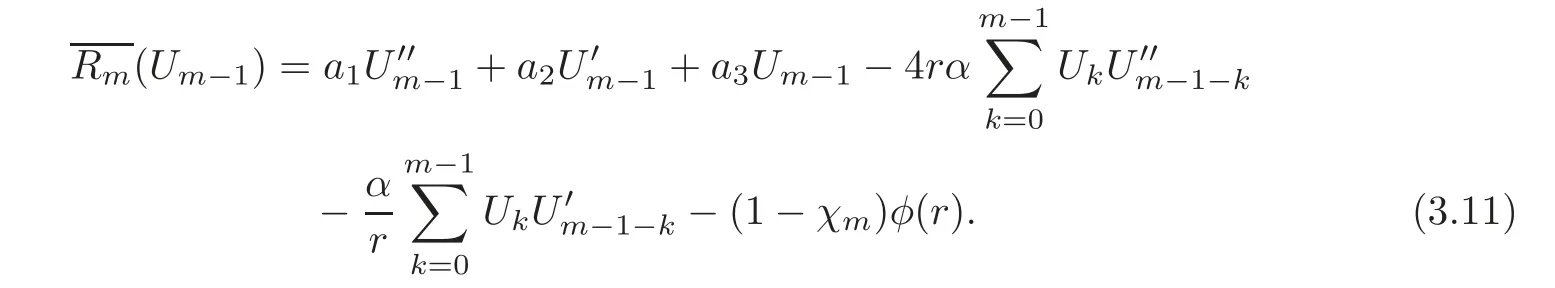
Applying the Chebyshev pseudospectral transformation to equations(3.9)–(3.11)gives

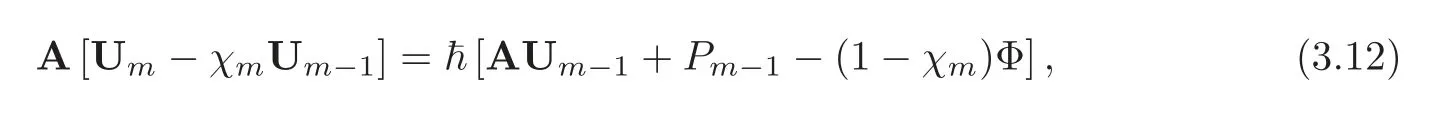
subject to the boundary conditions

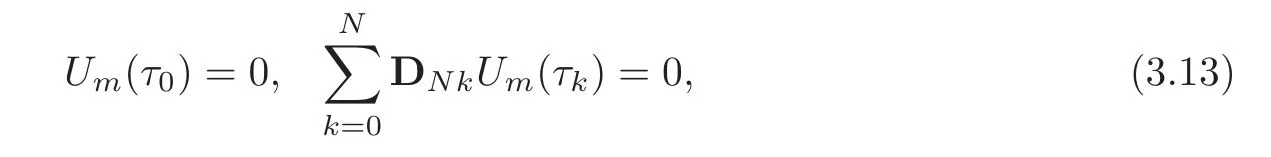
whereAand Φ satisfy(3.8)and

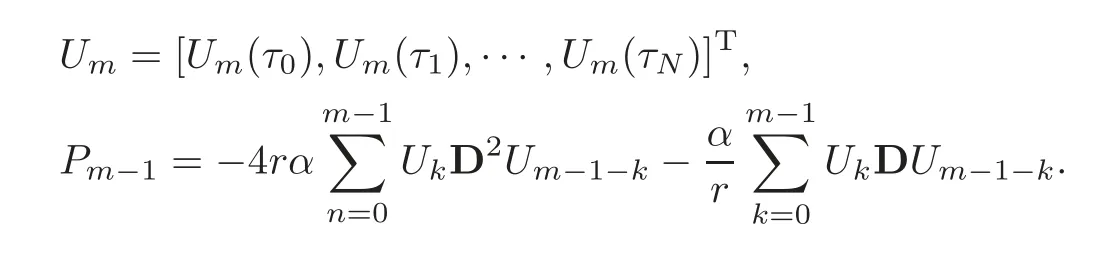
To implement the boundary conditions(3.13),we delete the first and last rows ofPm?1and Φ as well as the first and last rows and the first and last columns ofAin(3.12).This results in the following recursive formula form≥1:

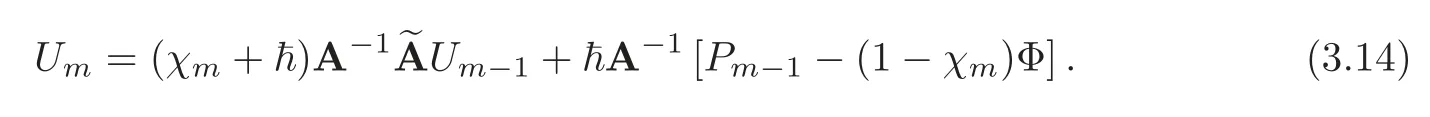
Thus,starting from the initial approximation,which is obtained from(3.8),higher order approximationsUm(τ)form≥1 can be obtained through the recursive formula(3.14).

4 Analysis and Numerical Simulation

In this section,we give the SHAM results for solving the nonlinear boundary value problem for the electrohydrodynamic flow of a fluid in an ion drag configuration in a circular cylindrical conduit.The results of SHAM have been compared with a numerical method,and we use a Runge-Kutta shooting method.We observe that in Table 1,the values obtained for the square residual error of SHAM are far less than standard HAM,and Figure 2 shows the solutions afterm=2 algorithm iterations,compared with the Matlab ode45.In Figures 3–6,the-curves form=2,4,6,8 order of the SHAM approximation,whenα=1,0.5 and for different values ofH2,are plotted so that SHAM is far more efficient than standard HAM.It was found that the

optimal value ofthat gives accurate results is the value at which the maximum of the 2nd order SHAM-curve is located.We also note that the SHAM results seem to converge at the 2nd order of approximation.But,convergence of the HAM results is not achieved even at the 20th order of HAM approximation.

Table 1 The optimal values offor all of the cases considered are obtained by minimizing EN(.

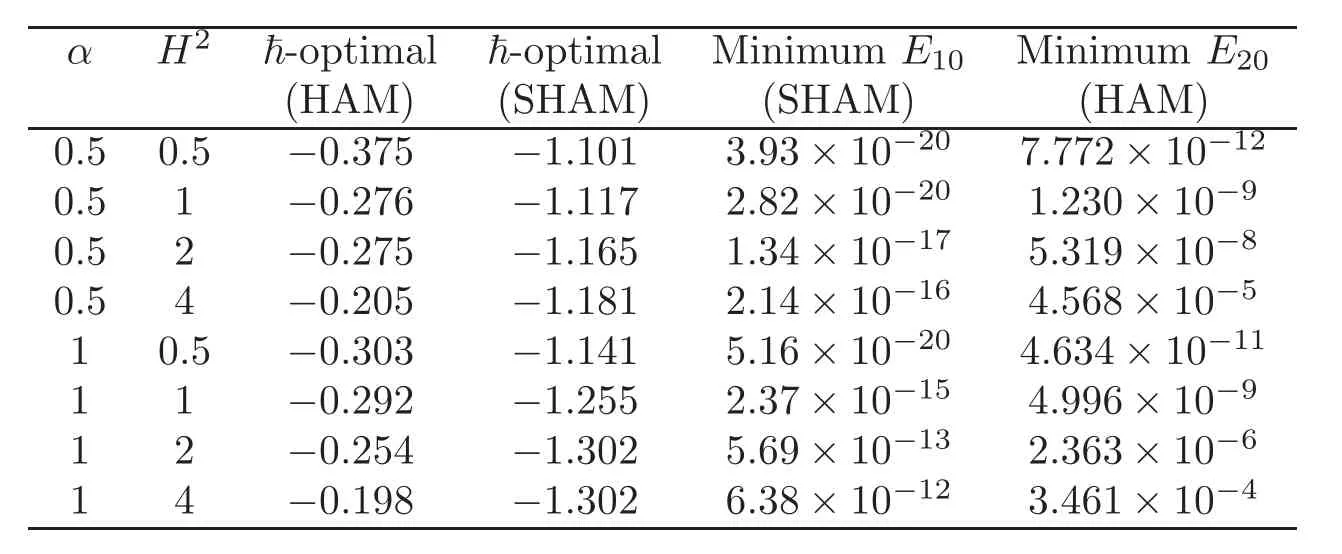
Table 1 The optimal values offor all of the cases considered are obtained by minimizing EN(.

αH2?-optimal?-optimalMinimum E10Minimum E20(HAM)(SHAM)(SHAM)(HAM)0.50.5?0.375?1.1013.93×10?207.772×10?12 0.51?0.276?1.1172.82×10?201.230×10?9 0.52?0.275?1.1651.34×10?175.319×10?8 0.54?0.205?1.1812.14×10?164.568×10?5 10.5?0.303?1.1415.16×10?204.634×10?11 11?0.292?1.2552.37×10?154.996×10?9 12?0.254?1.3025.69×10?132.363×10?6 14?0.198?1.3026.38×10?123.461×10?4

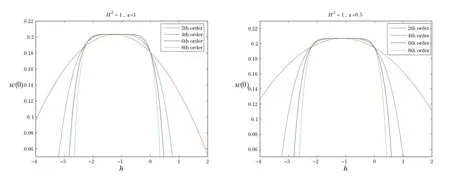
Figure 3 SHAM-curve at different orders of approximation when α=1,0.5 and H2=1.

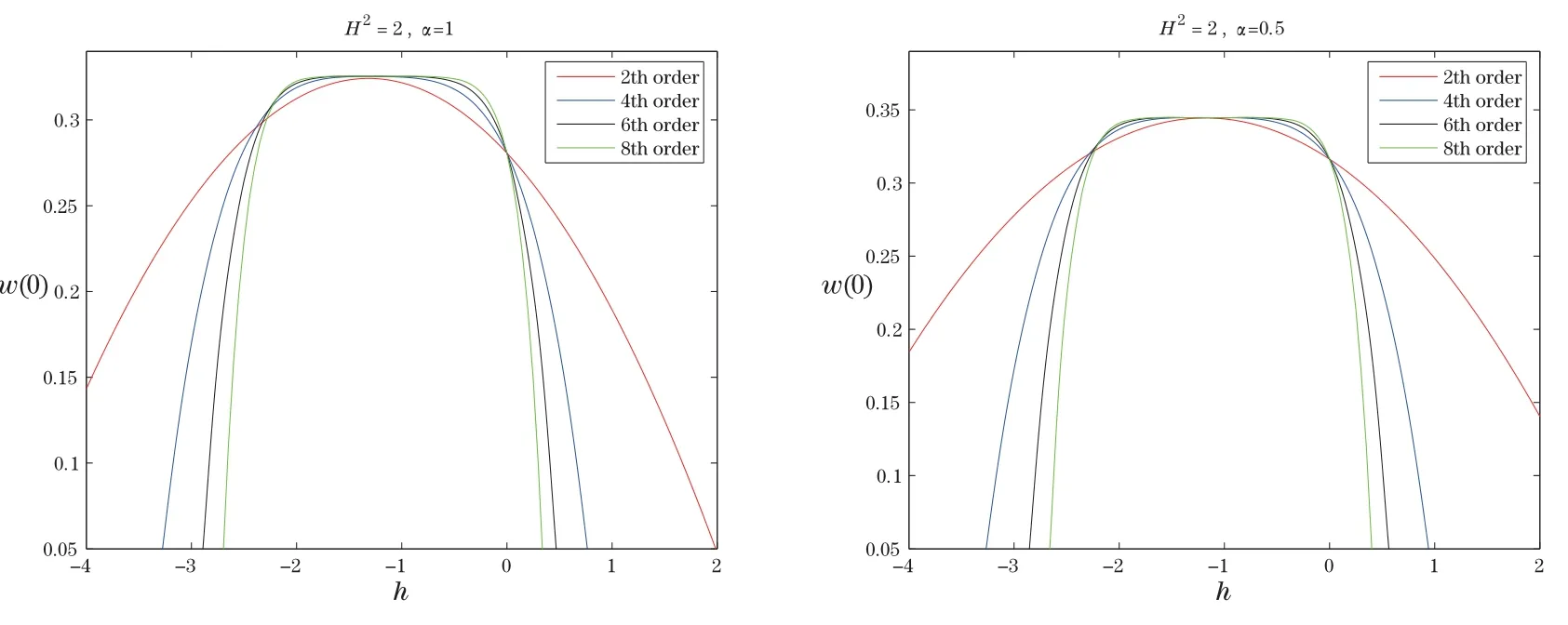
Figure 4 SHAM-curve at different orders of approximation when α=1,0.5 and H2=2.

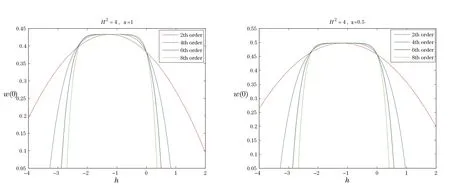
Figure 5 SHAM-curve at different orders of approximation when α=1,0.5 and H2=4.

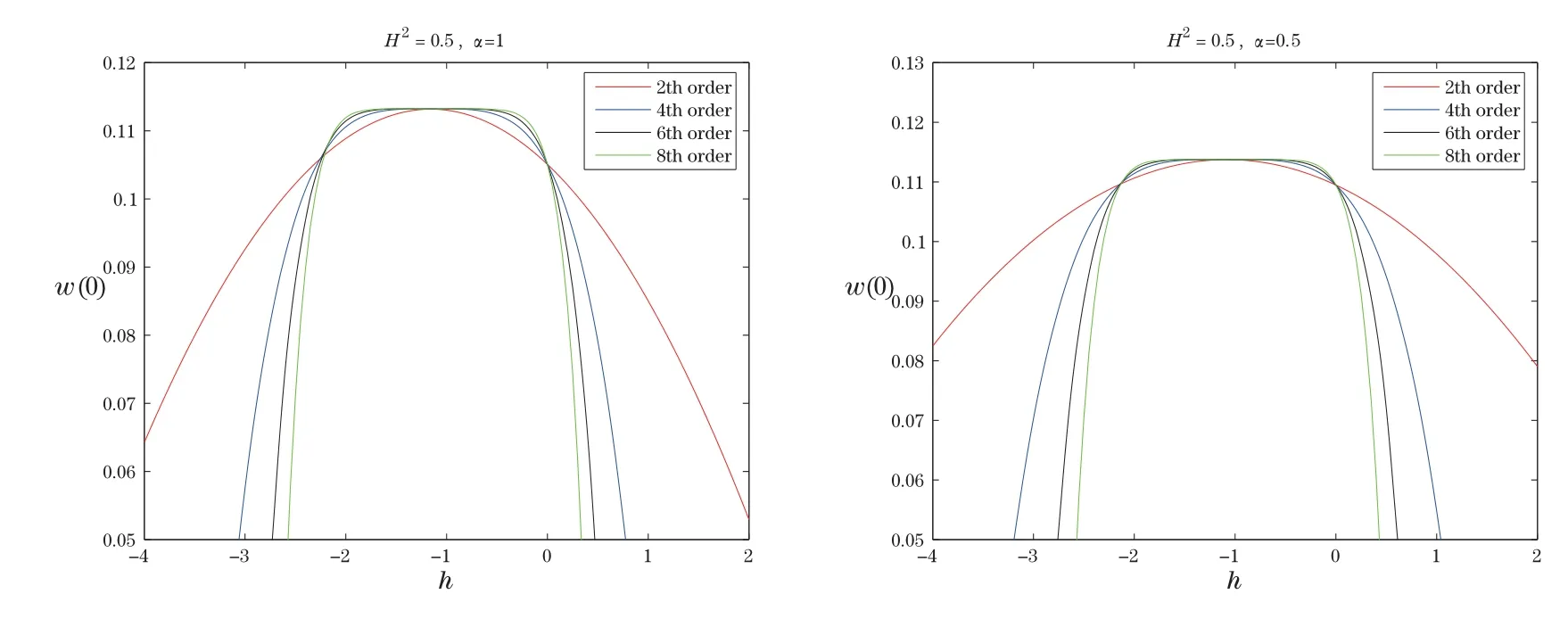
Figure 6 SHAM-curve at different orders of approximation when α=1,0.5 and H2=0.5.

We now use a new residual function for the SHAM as

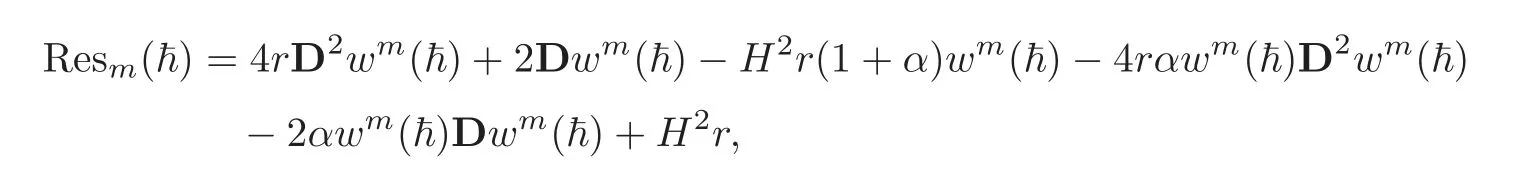
wherer=[r0,r1,···,rN]T,Resm=[Resm,Resm,···,Resm]T,wm=[wm,wm,···,wm]T=which has been obtained from the recursive formula(3.14),D is the Chebyshev spectral dif f erentiation matrix andmis the order of iteration.The graphs of the residual function Res(r)are shown in Figures 7–10 for the optimal value of?and all the cases considered are form=10.Furthermore,we use the so-called optimization method to f i nd out the optimal convergence-control parameters by means of the minimum of the averaged residual error(see[22])as

where Resm,idenote the elements of vector[Res]2fori=0,···,N.It is worth noting that vector[Res]2is def i ned with the property of the dot product in the Matlab software.Obviously,Em0(asm+∞)corresponds to a convergent series solution.For a given ordermof approximation,the optimal value ofis given by a nonlinear algebraic equation

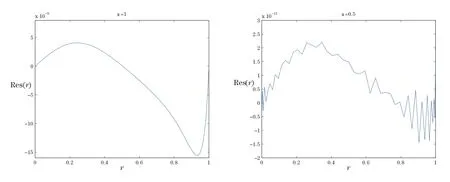
Figure 7The residual function of 10th order approximation SHAM for α=1,0.5 and H2=1.

The optimal values offor all the cases considered are obtained by minimizing the averaged residual error(4.1),which are given in Table 1.As Table 1 and Figures 7–10 confirm,the new approach leads to faster convergence in comparison with the standard HAM approach.Therefore,it is reasonable to use the SHAM instead.

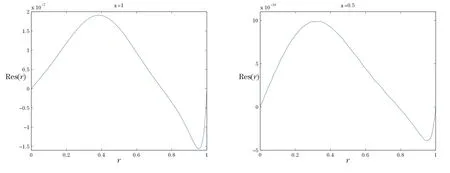
Figure 8 The residual function of 10th order approximation SHAM for α=1,0.5 and H2=2.

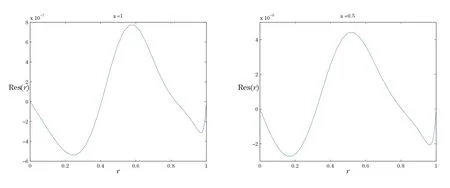
Figure 9 The residual function of 10th order approximation SHAM for α=1,0.5 and H2=4.

5 Conclusion

In this paper,we presented a new application of the spectral homotopy analysis method in solving the nonlinear boundary value problem for the electrohydrodynamic flow of a fluid in an ion drag configuration in a circular cylindrical conduit.The approximate SHAM numerical results are compared with results generated by using the standard HAM and ode45 from Matlab.This confirms the validity of the proposed SHAM approach as a suitable method for solving a wide variety of boundary value problems.

[1]Mckee,S.,Calculation of electrohydrodynamic flow in a circular cylindrical conduit,Z.Angew Math.Mech.,77,1997,457–465.

[2]Paullet,J.E.,On the solutions of electrohydrodynamic flow in a circular cylindrical conduit,Z.Angew Math.Mech.,79,1999,357–360.

[3]Hosseini,F.H.,Saberi Nik,H.and Buzhabadi,R.,Homotopy analysis method for solving foam drainage equation with space-and time-Fractional derivatives,International Journal of Differential Equations,2011,DOI:10.1155/2011/237045.

[4]Effati,S.,Saberi Nik,H.and Buzhabadi,R.,Solving famous nonlinear coupled equations with parameters derivative by homotopy analysis method,International Journal of Differential Equations,2011,DOI:10.1155/2011/545607.

[5]Zhang,Z.Y.,Li,Y.X.,Liu,Z.H.and Miao,X.J.,New exact solutions to the perturbed nonlinear Schr¨odingers equation with Kerr law nonlinearity via modified trigonometric function series method,Commun.Nonlinear Sci.Numer.Simulat.,16(8),2011,3097–3106.

[6]Zhang,Z.Y.,Gan,X.Y.,Yu,D.M.,et al.,A note on exact traveling wave solutions of the perturbed nonlinear schrodinger’s equation with Kerr law nonlinearity,Commun.Theor.Phys.,57,2012,764–770.

[7]Liao,S.J.,The proposed homotopy analysis technique for the solution of nonlinear problems,Shanghai Jiao Tong University,1992.

[8]Liao,S.J.,On the homotopy anaylsis method for nonlinear problems,Appl.Math.Comput.,147,2004,499–513.

[9]Liao,S.J.,Comparison between the homotopy analysis method and homotopy perturbation method,Appl.Math.Comput.,169,2005,1186–1194.

[10]Liao,S.J.,Homotopy analysis method:a new analytical technique for nonlinear problems,Commun.Nonlinear Sci.Numer.Simulat.,2(2),1997,95–100.

[11]Hayat,T.,Javed,T.and Sajid,M.,Analytic solution for rotating flow and heat transfer analysis of a third-grade fluid,Acta Mech.,191,2007,219–229.

[12]Abbasbandy,S.,Soliton solutions for the 5th-order KdV equation with the homotopy analysis method,Nonlinear Dyn.,51,2008,83–87.

[13]Zhu,S.P.,An exact and explicit solution for the valuation of American put options,Quantitative Finance,6,2006,229–242.

[14]Motsa,S.S.,Sibanda,P.and Shateyi,S.,A new spectral-homotopy analysis method for solving a nonlinear second order BVP,Commun.Nonlinear Sci.Numer.Simulat.,15,2010,2293–2302.

[15]Motsa,S.S.,Sibanda,P.,Awad,F.G.and Shateyi,S.,A new spectral-homotopy analysis method for the MHD Jeffery-Hamel problem,Computer and Fluids,39,2010,1219–1225.

[16]Saberi Nik,H.,Effati,S.,Motsa,S.S.and Shirazian,M.,Spectral homotopy analysis method and its convergence for solving a class of nonlinear optimal control problems,Numer.Algor.,65,2014,171–194.

[17]Saberi Nik,H.,Effati,S.,Motsa,S.S.and Shateyi,S.,A new piecewise-spectral homotopy analysis method for solving chaotic systems of initial value problems,Mathematical Problems in Engineering,2013,DOI:org/10.1155/2013/583193.

[18]Mastroberardino,A.,Homotopy analysis method applied to electrohydrodynamic flow,Commun.Nonlinear Sci.Numer.Simulat.,16,2011,2730–2736.

[19]Liao,S.J.,Beyond Perturbation:Introduction to Homotopy Analysis Method,Chapman and Hall/CRC Press,Boca,Raton,London,New Yrok,Washington,2003.

[20]Canuto,C.,Hussaini,M.Y.,Quarteroni,A.and Zang,T.A.,Spectral Methods in Fluid Dynamics,Springer-Verlag,Berlin,1988.

[21]Trefethen,L.N.,Spectral Methods in MATLAB,SIAM,Philadelphia,2000.

[22]Liao,S.J.,An optimal homotopy-analysis approach for strongly nonlinear differential equations,Commun.Nonlinear Sci.Numer.Simulat.,15,2010,2003–2016.