Zhaoying WEI Guangsheng WEI

1 Introduction

In this paper,we are concerned with the Dirac operatorH:=H(p(x),r(x);α,β)which is formulated as

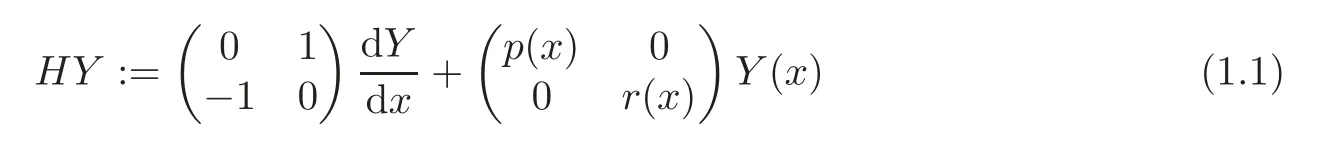
forx∈[0,π],subject to the self-adjoint separated boundary conditions

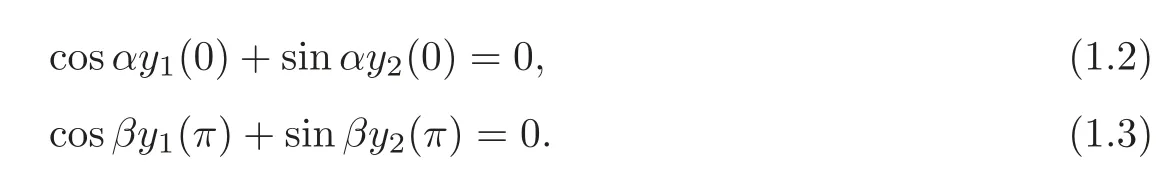
HereY(x)=(y1(x),y2(x))T,α,β∈[0,π)and the potentialsp(x),r(x)∈L2[0,π]are all realvalued.It is known(see[1])that the operatorHis self-adjoint inL2[0,π]×L2[0,π]and has a real simple discrete spectrum,denoted byσ(H):={λn}n∈Z{0},accumulating at?∞and+∞.

It is well known(see[1–2])that the potentialspandrof the Dirac operatorHdefined by(1.1)–(1.3)are uniquely determined in terms of one of the following three sets of spectral data:

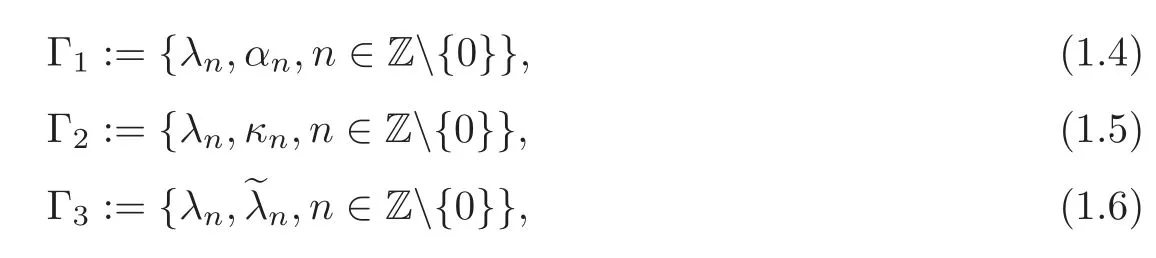
whereis the eigenvalue of the same problem as(1.1)–(1.3)but withβin(1.3)replaced by(β),κnis called the terminal velocitie(or a norming constant)andαnis called a normalized constant corresponding to eigenvalueλn,which are defined as

and

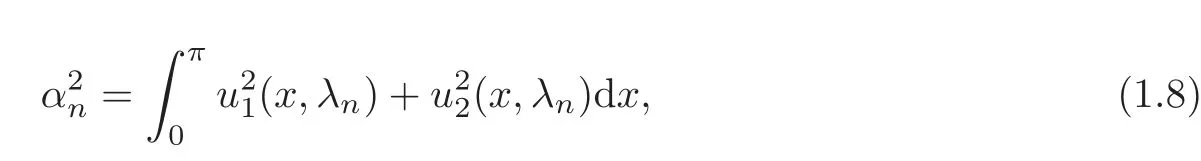
respectively.Here(u1(x,z),u2(x,z))T=:U(x,z)is the solution of the Dirac equationH(Y)=zYwith the initial conditions

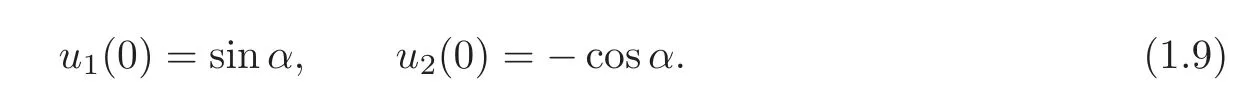
The present paper will mainly investigate the uniqueness problem of the determination of the potentialspandrunder the circumstances,where only partial information of(p,r),the eigenvaluesand the norming constantsare available.

In 1996,Amour[3]proved the half-inverse theorem for the Dirac operators,which says that the Dirichlet spectrum(that isα=0=βin(1.2)–(1.3))determines the potentials(p,r)uniquely provided that the potentials(p,r)are given a priori on the half-left(or half-right)of the interval[0,π].This result is a generation of Hochstadt and Lieberman’s theorem(see[4])for Sturm-Liouville operators.Furthermore,in 2001,Delrio and Grbert[5]considered the case where the potentials are a priori known on[a,π]with 0≤a<πand proved that this together with a part of two spectra determines the potentials(p,r)uniquely on[0,π].This result can be viewed as a parallel one of Gesztesy and Simon’s theorems(see[6,Theorem 1.3])for the Sturm-Liouville problems.

For the question of uniqueness of the inverse Sturm-Liouville problems,Wei and Xu in[7]showed that norming constants play an equal role as eigenvalues.They obtained some uniqueness results for Sturm-Liouville problems,analogous to the theorems of Gesztesy-Simon(see[6])and Hochstadt-Lieberman(see[4]),which imply that the potentialqcan be completely determined even if partial information is given onqtogether with partial information on the spectral data Γ1or Γ2.

The main aim of the present paper is to generalize the results of[7]to the Dirac operators.More specifically,we will show that the pair of potentials(p(x),r(x))and a boundary condition are uniquely determined even if only partial information is given on(p(x),r(x))together with partial information on the spectral data,consisting of either one full spectrum and a subset of norming constants,or a subset of pairs of eigenvalues and the corresponding norming constants.Moreover,we also concern with the situation in which bothp(x)andr(x)areCn-smoothness at some given point.

Throughout this paper,for anyS?σ(H),the statement that the setSis almost symmetric means thatλn∈Sforn∈N implyλ?n∈Swith finitely many possible exceptions.For eacht≥0,we define

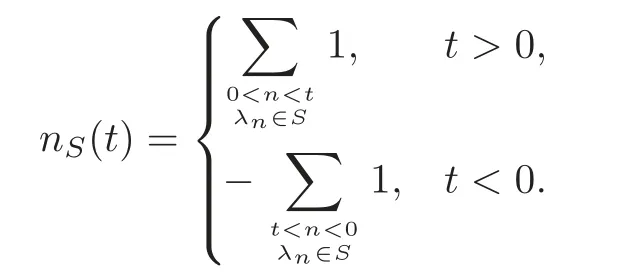
We state the main results of this paper through two cases.We first treat the case of one full spectrum and a subset of norming constants to be known.The other case that the known eigenvalues and norming constants are pairs will be treated in Theorem 1.2 below.

Theorem 1.1Let aand p(x),r(x)∈Cn(a?ε,a+ε)for some n∈Nand ε>0.

Let the subset S?σ(H)be almost symmetric such that κjare known for λj∈S.Suppose that

exists,and for μ1∈R,t0>0,

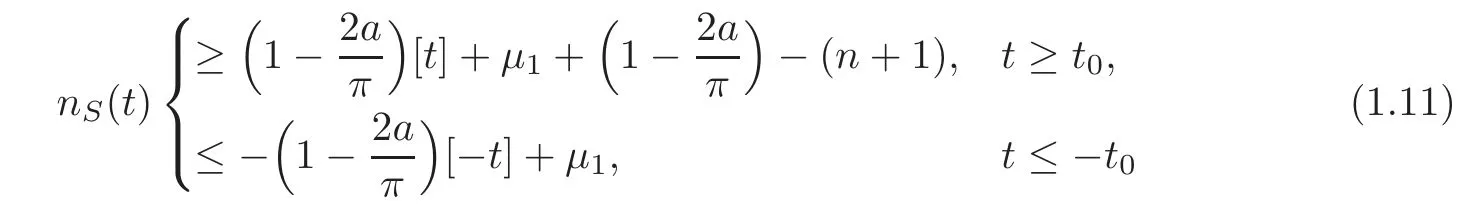
for all t∈R.Then the potentials(p(x),r(x))on[0,a]together with(p(j)(a),r(j)(a))(j=1,2,···,n),κjcorresponding to λj∈S,and σ(H)uniquely determine β and the potentials(p(x),r(x))on[0,π].

Let us mention that ifp(x),r(x)∈Cn(a?ε,a+ε),thennvalues of norming constants can be replaced by the values of(p(j)(a),r(j)(a))(j=1,2,···,n),that is,in the setS,nnorming constants can be missed.It should be noted that ifa=0 in the above theorem,that is,the knowledge of the potentials(p(x),r(x))is missing,then(p(x),r(x))on[0,π]are uniquely determined by Γ2:={λn,κn,n∈Z{0}}.

The following theorem treats the case that the known eigenvalues and norming constants are pairs.

Theorem 1.2Let a∈(0,π).Set the subset S?σ(H)be almost symmetric such that κj is known for λj∈S.Suppose that

exists,and for μ2∈R,t0>0,ε>0being an arbitrary number,

Then the potentials(p(x),r(x))on[0,a],λj∈S and the corresponding norming constants κj determine uniquely β and the potentials(p(x),r(x))on[0,π].

It is worth pointing out the special case wherewe only need half(e.g.the even or the odd)of the full spectrum and the corresponding norming constants to uniquely determine(p(x),r(x))on[0,π]andβ.In this situation,the problem reduces to Theorem 1 in[3],for which one can see that the other half of the spectrum is replaced by half of the norming constants.

The method we use to obtain our results is based on the uniqueness theorem of Weyl-Titchmarsh-m-function(see[8–9]).This approach has been employed skillfully by Del Rio,Gesztesy and Simon in a series of papers(see[10–12])to deal with inverse problems.The key technique relies on the asymptotic expansion of anm-function.

The organization of this paper is as follows.In Section 2,we give some preliminaries to our problems.The proofs of our theorems are presented in Section 3.

2 Preliminaries

We begin by recalling some classical results,which will be needed later.LetU(x,z)=(u1(x,z),u2(x,z))TandV(x,z)=(v1(x,z),v2(x,z))Tdenote the solutions of the equation

forx∈[0,π],with the initial conditions

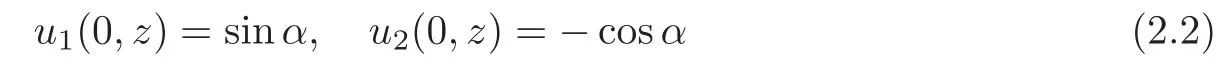
and

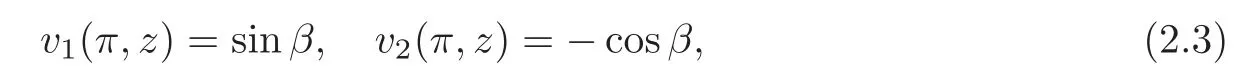
respectively.It is known(see[1])that,as|z|→∞in C,the following asymptotic formulae are uniformly inx∈[0,π]:

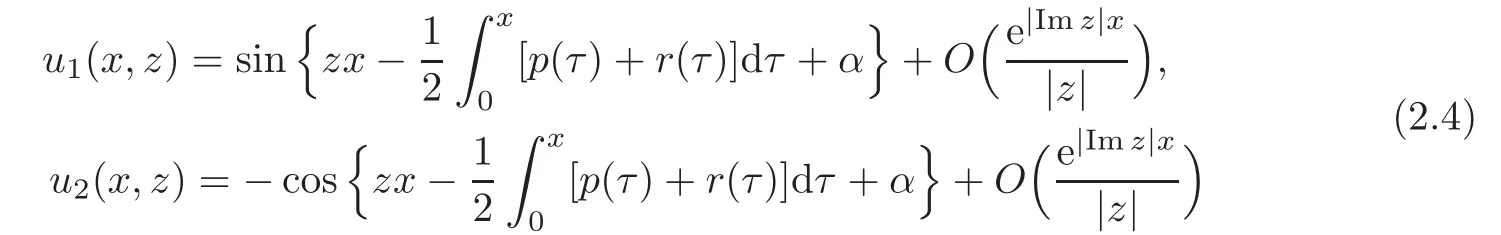
and

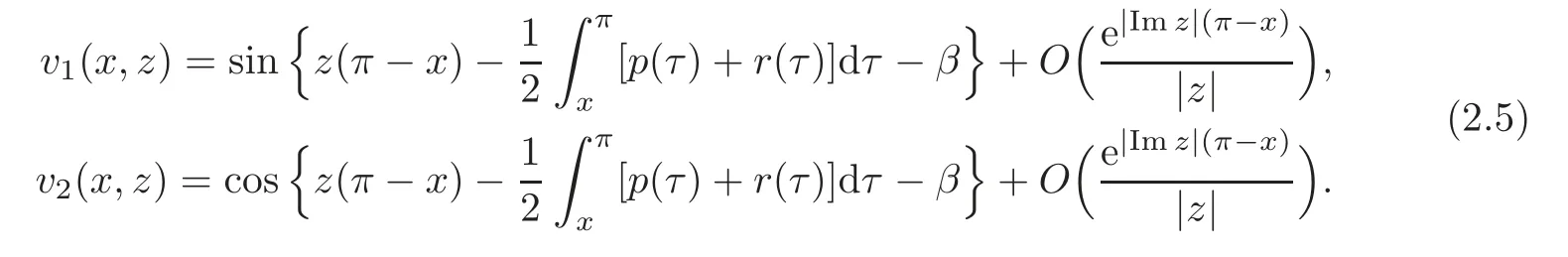
As is well known,the eigenvalues{λj}j∈Z{0}of operatorHhave the asymptotic formula

asj→∞,where Note thatU(x,λj)andV(x,λj)are eigenfunctions corresponding to the eigenvalueλj.From(1.2)we see that if sinαsinβ0,then the norming constantκjassociated withλjis

that is,otherwise,κjcan be represented by

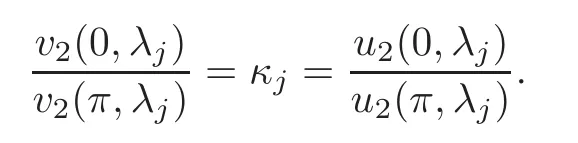
Let us introduce the Weyl-Titchmarsh-mfunction(see[13])for the operatorH,which reads as

Note thatm(x,z)is the Herglotz function,that is,m:C+→C+is analytic,and it has the following asymptotic formula:

which is uniformly inx∈[0,π?δ]forδ>0,as|z|→∞in any sectorε0.Furthermore,letωbe a number from the intervaland let the setD?Z be determined thus by

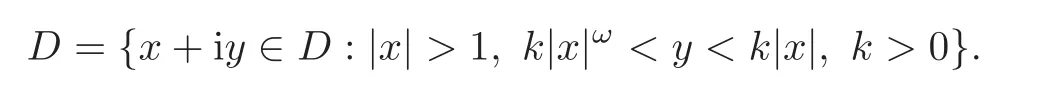
If the potentialsp(x),r(x)belong to the classCN[0,δ)for someδ>0,then,for allz∈D,the high-energy asymptotic expansion of the Weyl-Titchmarsh-mfunction holds(see[14]):

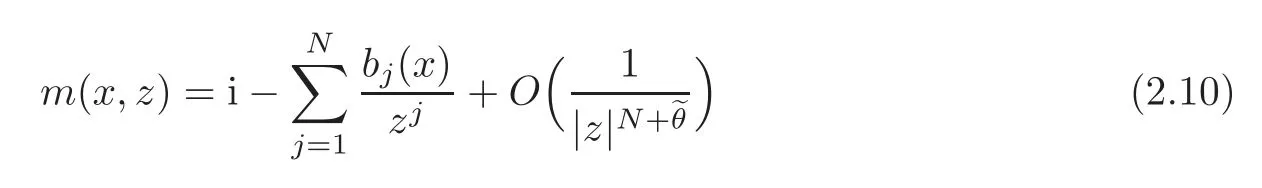
asz=x+iy(∈D)→∞,where=1?(1?ω)(N+3)and the functionsbj(x)are given by the recursive equalities:

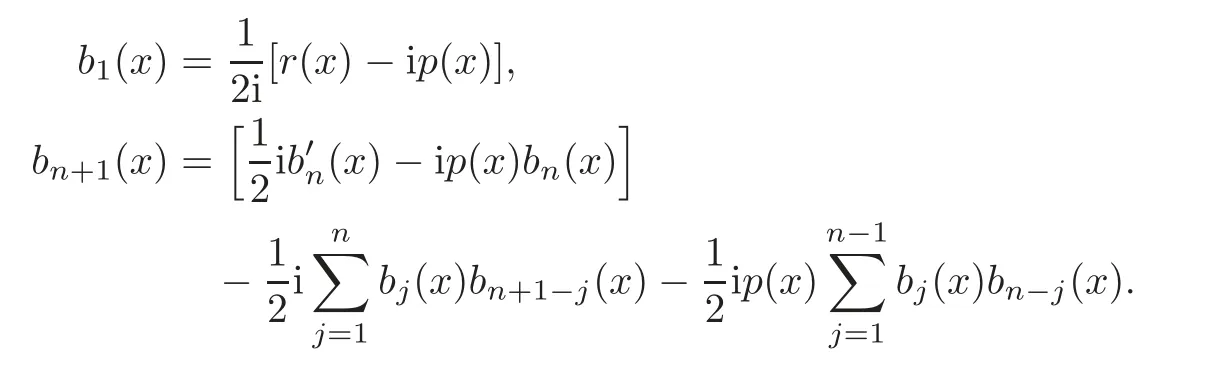
With the above preliminaries out of way,in order to prove Theorem 1.1 and Theorem 1.2,let(p(x),r(x))be given on[0,a]and let(p1(x),r1(x)),(p2(x),r2(x))be two candidates for(p(x),r(x))extended to the interval[0,π].Denote bymj(x,z)them-function corresponding to operatorsHj:=H((pj(x),rj(x));α,βj)forj=1,2.

A similar statement of the Dirac operator to the uniqueness theorem of Marchenko(see[8])is the following lemma.

Lemma 2.1(see[8])If m1(a,z)=m2(a,z),then p1(x)=p2(x),r1(x)=r2(x)on[a,π]andtanβ1=tanβ2.

Finally,for functionsp(x),r(x)∈L2[0,π],we introduce the Green’s formula associating with(1.1)which reads as following:

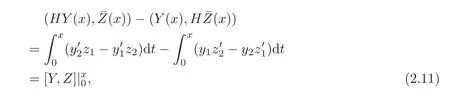
whereY(x)=(y1(x),y2(x))T,andZ(x)=(z1(x),z2(x))T.Particularly,if bothY(x)=(y1(x),y2(x))TandZ(x)=(z1(x),z2(x))Tare solutions of(2.1),then[Y,Z](x)=[Y,Z](0)is a constant forx∈[0,π].

3 Proof of Theorems

In this section we give the proofs of our main results.LetUj=(uj,1(x,z),uj,2(x,z))TandVj=(vj,1(x,z),vj,2(x,z))Tforj=1,2 be solutions of the equation

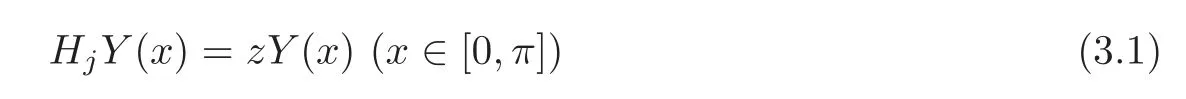
subject to the initial conditions

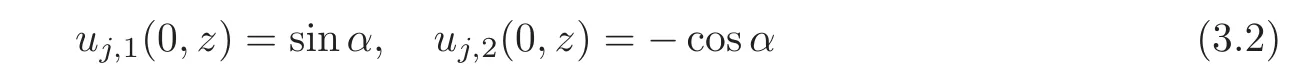
and

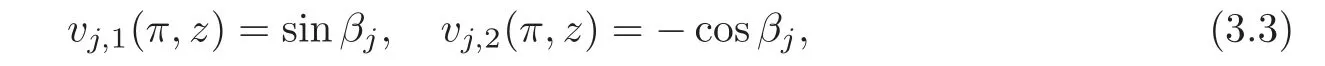
respectively.Let

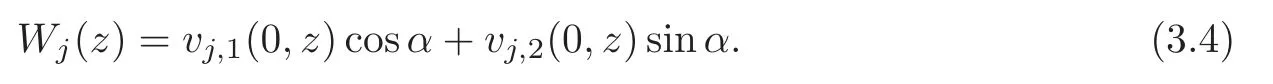
Then the zeros of equationsWj(z)=0 coincide with the eigenvaluesof the operatorsHj,whereWj(z)are called the characteristic functions ofHj.

In virtue of(2.5),we infer that ifz=iywithy∈R,we have

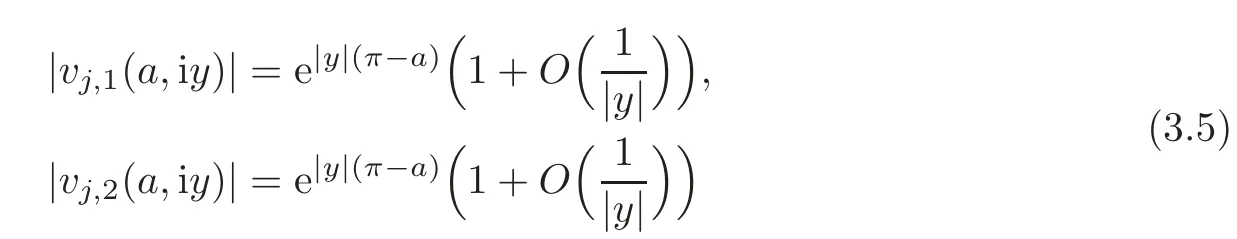
asy→∞.This together with(3.4)yields

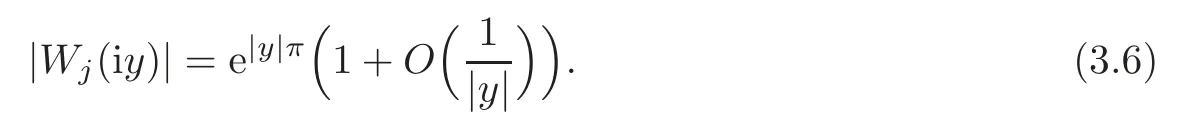
For our purpose of this paper,we need the following Lemmas 3.1–3.4.

Lemma 3.1(see[15])Let zn,n≥1be complex numbers with

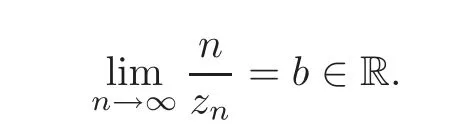
Suppose further that for some c>0,|zn?zm|≥c|n?m|.Let

Then for any ε>0,as r=|z|→∞,

and

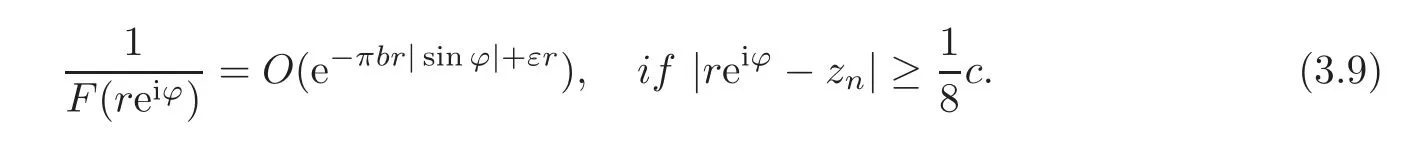
Lemma 3.2(see[16])Let F(z)be an entire function of the zero exponential type,i.e.,

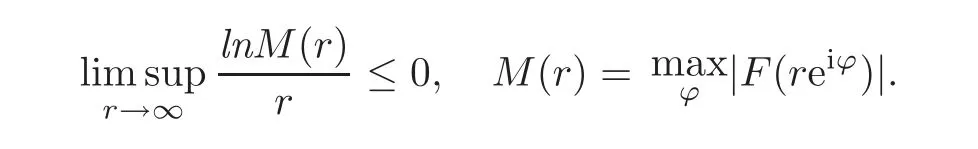
If F(z)is bounded along a line,then F(z)is a constant.In particular,if F(z)→0when|z|→∞along a line,then F(z)≡0.

Lemma 3.3Let σ(Hj)be the sets of eigenvalues of operators Hjfor j=1,2.If σ(H1)=σ(H2),then the characteristic functions W1(z)=W2(z).

ProofLetbe the eigenvalues ofHjforj=1,2.It is known that the characteristic functionsWj(z)of the operatorsHj,defined by(3.4),are entire functions inzof order 1,and consequently by Hadamard’s factorization theorem(see[17,p.289]),which are uniquely determined up to a multiplicative constant by their zeros:

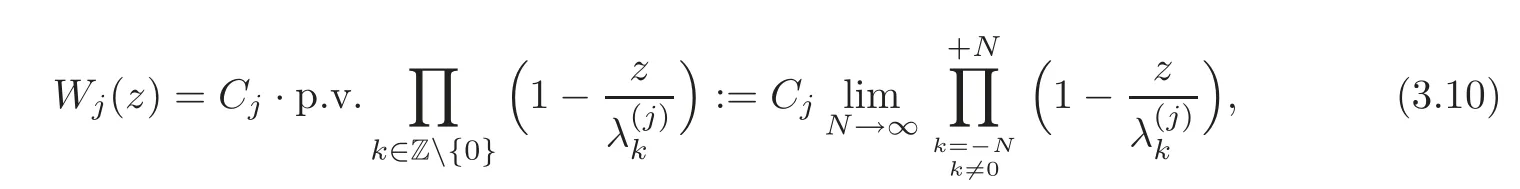
whereCjis some constant.Furthermore,recalling Green’s formula(2.11)and(3.4),Wj(z)=cosβjuj,1(π)+sinβjuj,2(π).It follows from(2.4)that

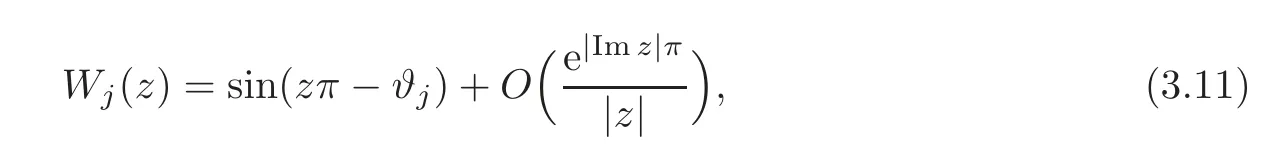
whereConsider the functions

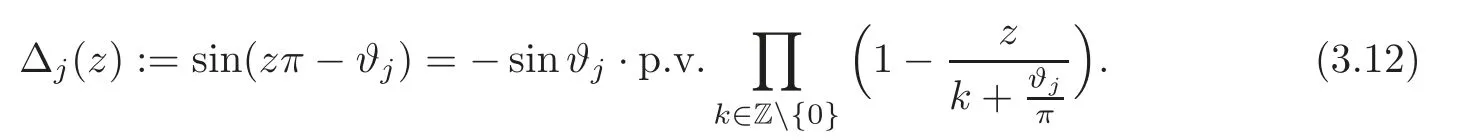
These together with(3.10)yield

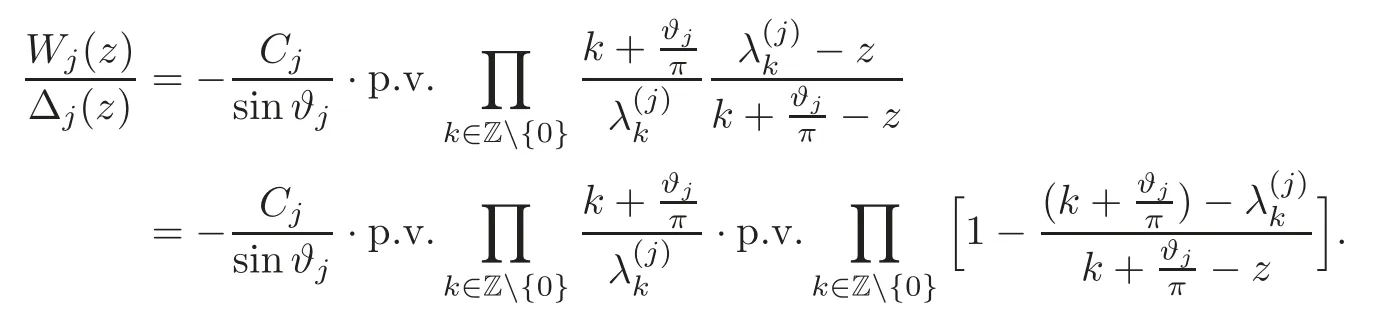
Sincefrom(3.11)and(3.12),it follows that

Sincetaking the asymptotic formulae ofand(see(2.6))into account we calculate?1=?2and thereforeC1=C2.This impliesW1(z)=W2(z)and completes the proof.

Lemma 3.4For j=1,2,letandbe the eigenvalues and normingconstants of operators Hj,respectively.for n∈Z{0},andfor l largeenough,thensinβ1=sinβ2.

ProofTaking(2.5)intowe have

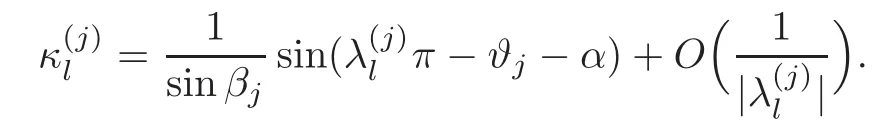
From the proof of Lemma 3.3,we know?1=?2.It follows from(2.6)that

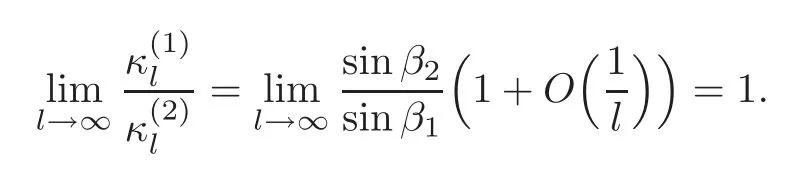
This shows sinβ1=sinβ2and completes the proof.

Basing on the above preliminaries,now we give the proofs of Theorems 1.1–1.2.

Proof of Theorem 1.1Define

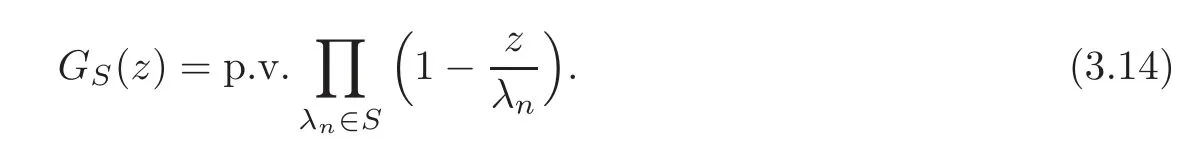
We prove first thatGS(z)is an entire function.Set

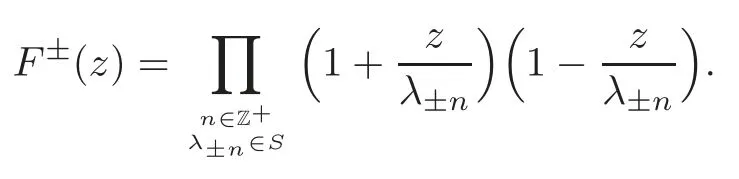
From Lemma 3.1,for anyε>0,we have

asr=|z|→∞,θ=Argz.Note that the setSis almost symmetrical,which implies

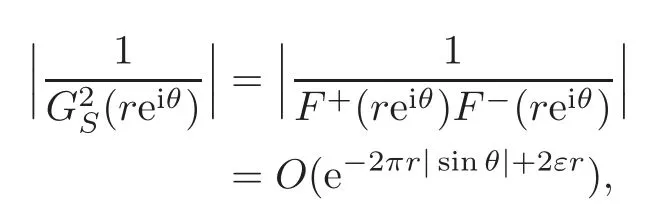
that is,

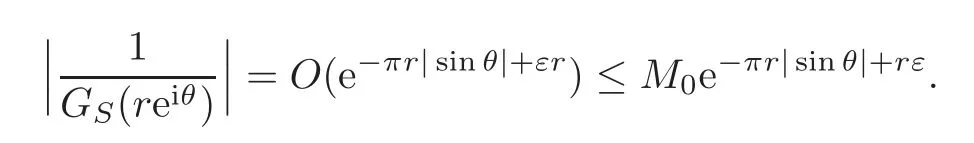
This shows thatGS(z)is of locally uniform convergence and hence it is an entire function with zeros{λn}.

Second,we give the estimation about the lower bound of|GS(iy)|.From(3.14),forz=x+iy,

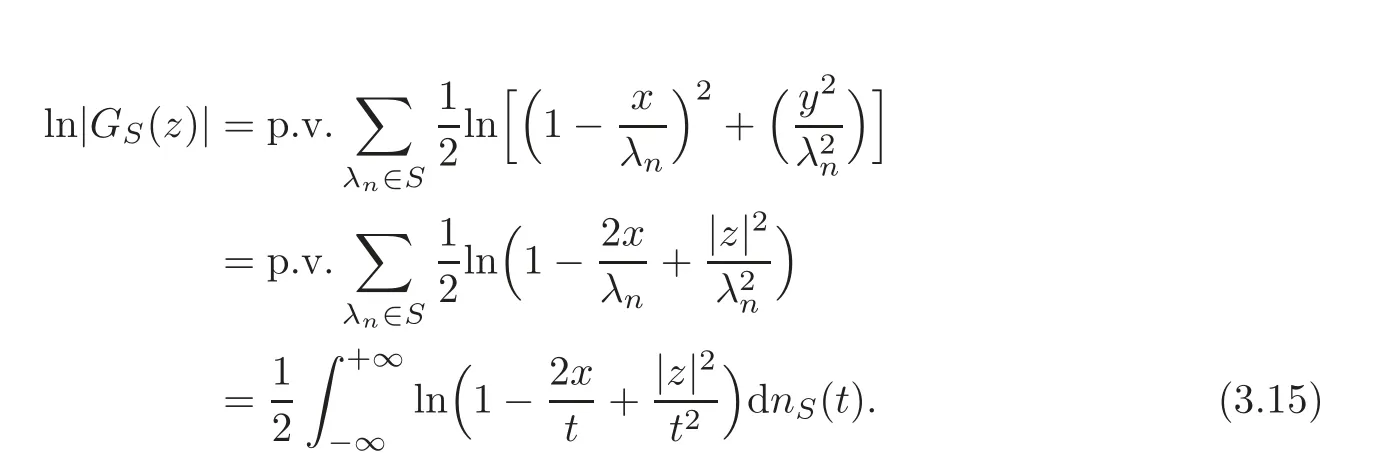
Integrating(3.15)by parts,we obtain

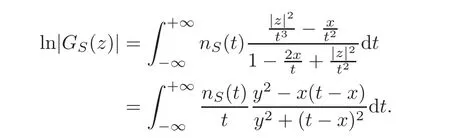
This yields

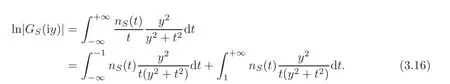
It is noted that

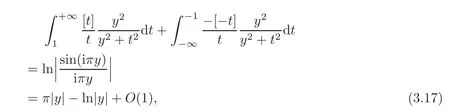
because of the known formula

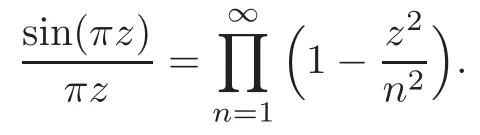
On the other hand,we have

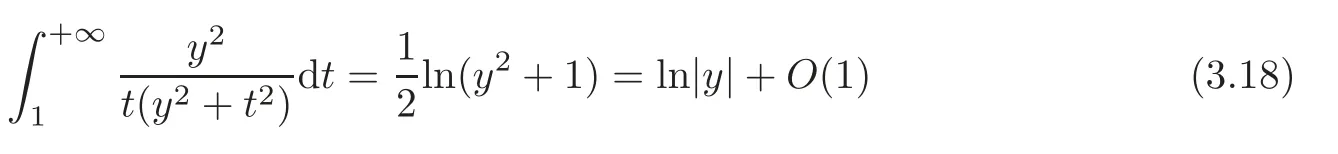
from the relation

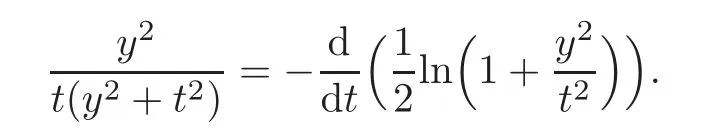
Analogously,we obtain

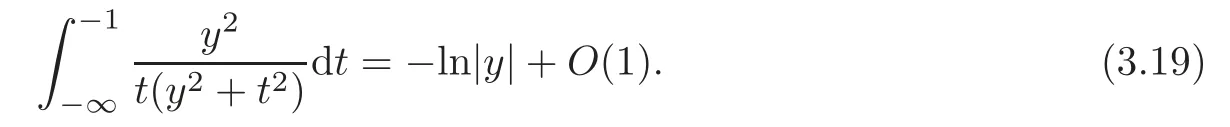
Taking the inequality(1.11)into(3.16)and using(3.18)–(3.19)and(3.23),we deduce that

It follows that

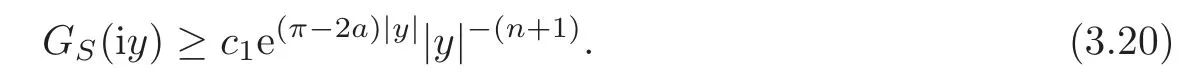
Finally,we complete the proof.Let(x,z)=(x,z),x,z))Tbe another solution of the equationH2Y=zYwith the initial conditions

where∈[0,π]andβ1,β2.It should be noted that,at the boundaryx=π,(x,z)satisfies

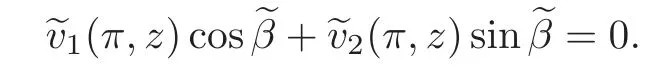
Consider the operatorH(p2,r2;α,.It is easy to see that its eigenvalues,denoted by{μn}n∈Z{0},are the zeros of the following equation:

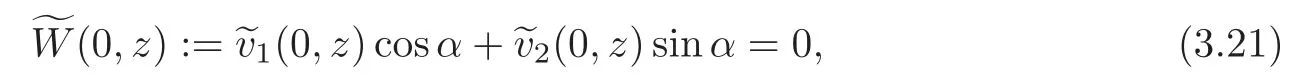
and the eigenvalues are interlaced and disjoint to the eigenvalues ofH(p2,r2;α,β)(see[18]).Define

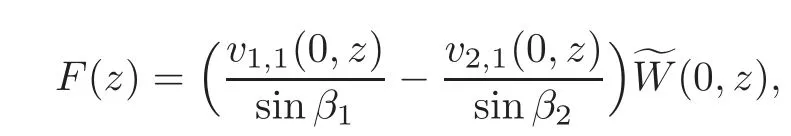
which implies thatF(μn)=0 for alln∈Z{0}.Furthermore,we haveF(λl)=0 for allλl∈Sbecause ofNoting thatW1(z)=W2(z)and sinβ1=sinβ2from Lemmas 3.3–3.4,by using the equations(3.4)and(3.21),we get

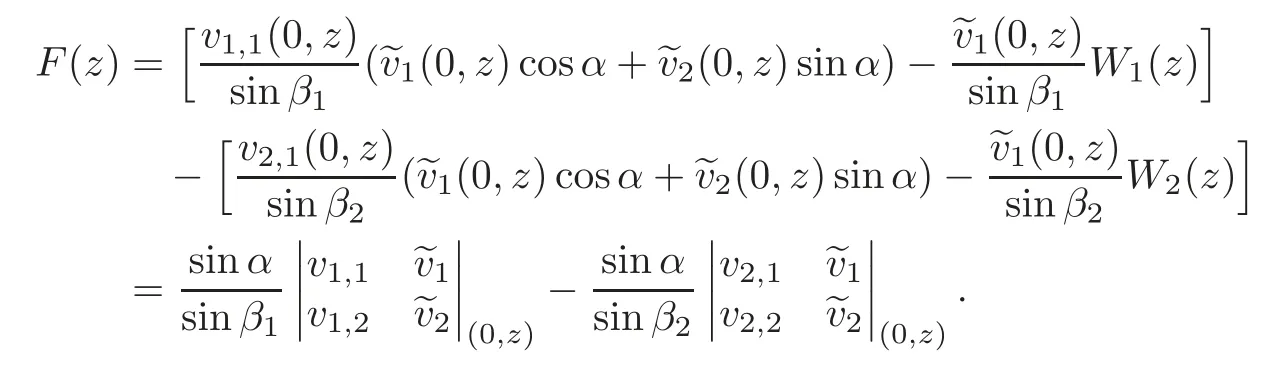
Sincep1(x)=p2(x)andr1(x)=r2(x)on[0,a],using the Green’s formulae(2.11)and(2.8),we have

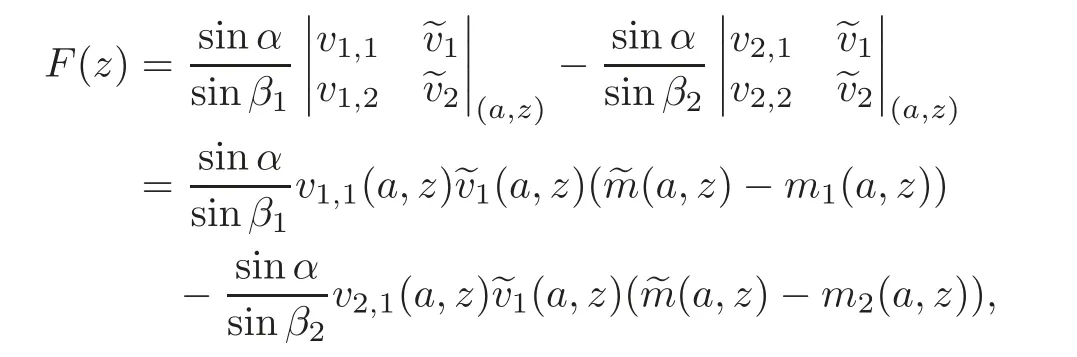
whereis the Weylm-function associating with the solution(x,z).Furthermore,since(a)forj=1,2,···,n,by using(2.10)and(3.5),we infer that

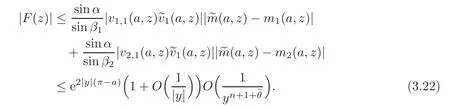
Let us defineH(z)by

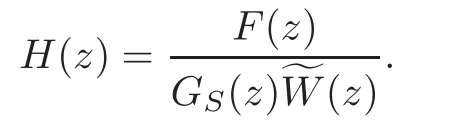
The cross ratioF(z)vanishes at each point whereGS(z(z)vanishes,and alsoGS(z)(z)necessarily has simple zeros sinceH(p2,r2;α,β2)andH(p2,r2;α,)have simple spectra,respectively,and their spectra are interlaced and disjointed.ThusH(z)is an entire function,and from(3.6),(3.20)and(3.22),we have

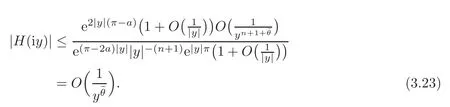
It turns out that|H(iy)|→0 asy→∞.By Lemma 3.2,we obtainH(z)≡0 for allz∈C.We can multiplyH(z)byGS(z),which has isolated zeros,so we conclude thatm1(a,z)=m2(a,z).From Lemma 2.1,we haveβ1=β2andp1(x)=p2(x),r1(x)=r2(x)on[a,π].The proof is completed.

Proof of Theorem 1.2Set

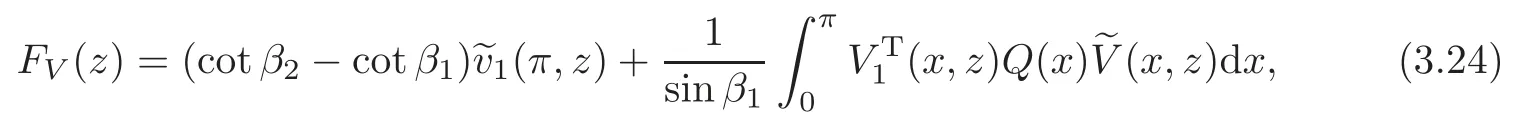
whereV1(x)=(v1,1(x),v1,2(x))T,(x)=(x),(x))TandQ(x)=diag(p1(x)?p2(x),r1(x)?r2(x)).Then from the initial conditions(3.3),we have

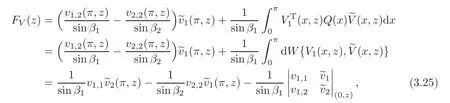
whereW{V1(x,z),(x,z)}is the Wronskian ofV1(x,z)and(x,z).Since

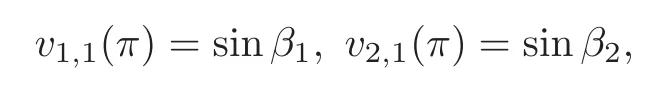
by using the Green’s formula(2.11),we have

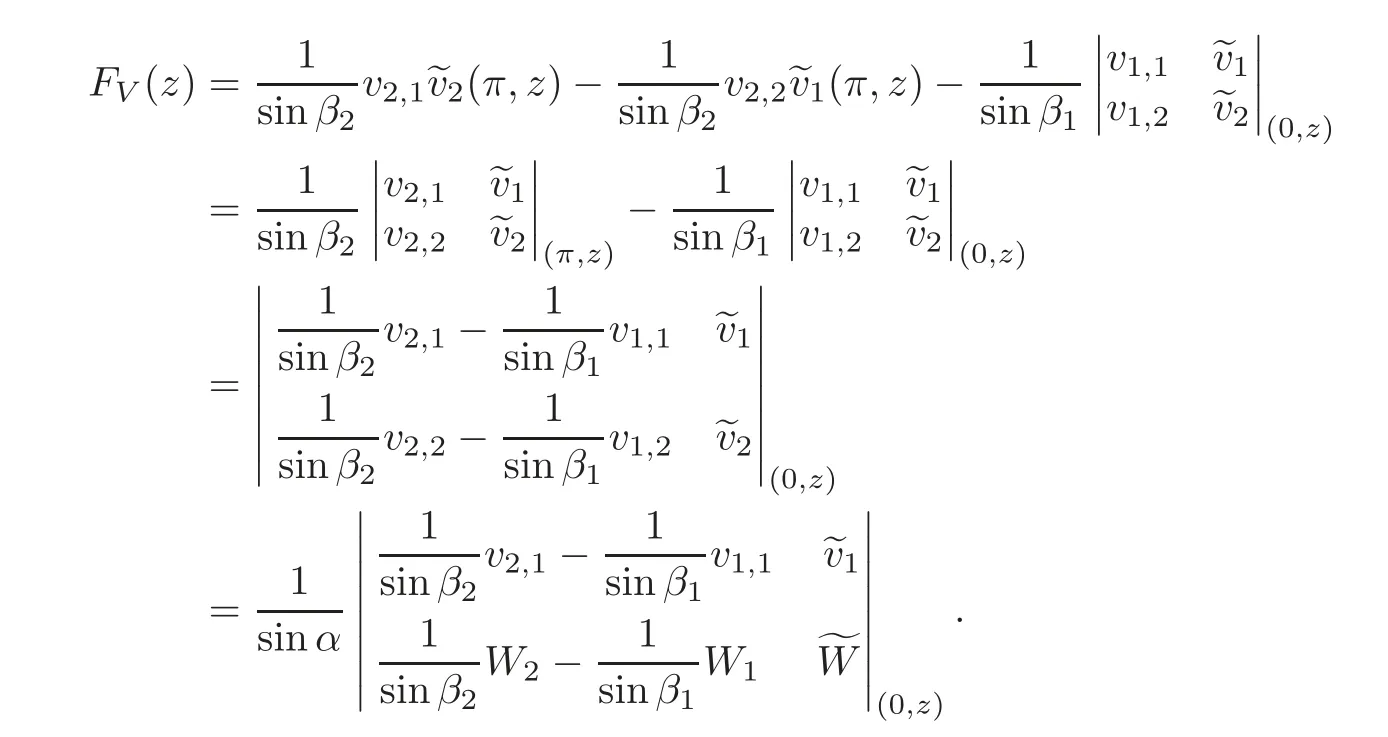
Note that ifλj∈S,thenThis shows thatFV(λj)=0.Furthermore,sincep1(x)=p2(x),andr1(x)=r2(x)on[0,a],it follows from(3.25)that

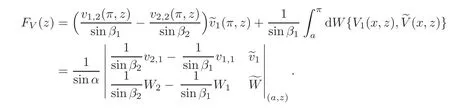
LetVD(x,z):=be the solution of the equationH2Y=zYsatisfying the initial conditions(a,z)=(0,1)T.Then

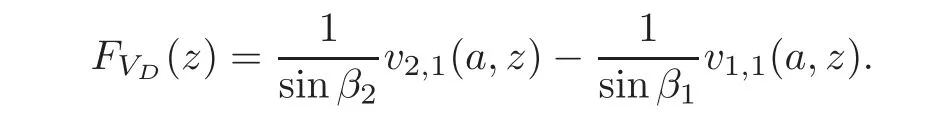
Defining

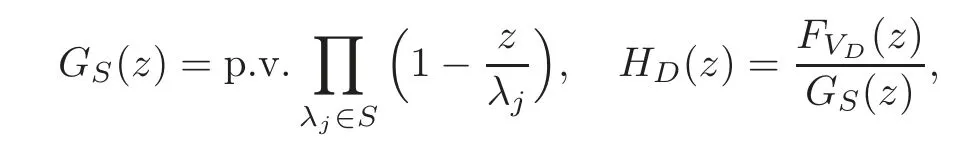
by the hypothesis onSand the arguments of the proof of Theorem 1.1,we have

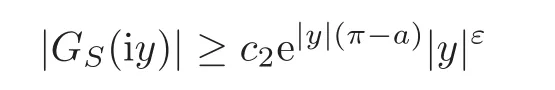
and

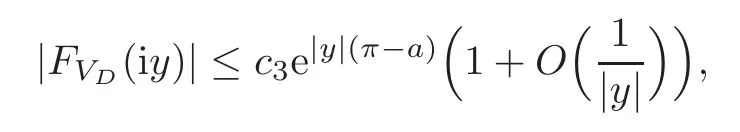
which yields

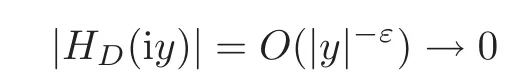
asy→∞.HenceHD(z)=0 andfor allz∈C.

LetVN(x,z):=be the solution of the equationH2Y=zYsatisfying the initial conditions(a,z)=(1,0)T.We have

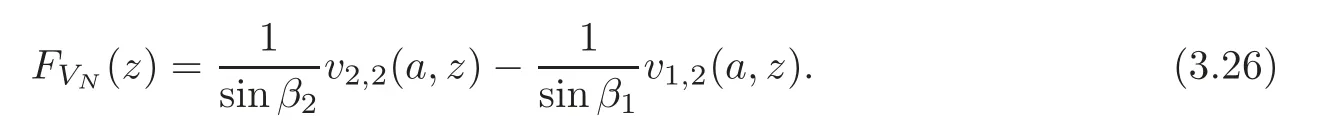
Define

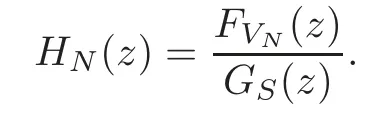
Sincefor allz∈C,from(2.9),(3.5),(3.20)and(3.26),we have

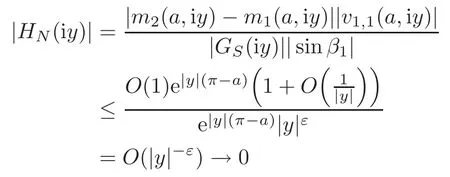
asy→∞.This showsHN(z)=0,andfor allz∈C.Thus we conclude thatm1(a,z)=m2(a,z).By Lemma 2.1,we havep1(x)=p2(x),r1(x)=r2(x)on[0,π],andβ1=β2.The proof is completed.

AcknowledgementThe authors would like to thank the referees for their helpful comments and suggestions which helped to improve and strengthen the presentation of the manuscript.

[1]Levitan,B.M.and Sargsjan,I.S.,Sturm-Liouville and Dirac operators,Nauka,Moscow,1988.

[2]Horv′ath,M.,On the inverse spectral theory of Schr¨odinger and Dirac operators,Amer.Math.Soc.Transl.,353(10),2001,4155–4171.

[3]Amour,L.,Extension on isospectral sets for AKNS system,Inverse problem,12(2),1996,115–120.

[4]Hochstadt,H.and Lieberman,B.,An inverse Sturm-Liouville problem with mixed given data,SIAM J.Appl.Math.,34(4),1978,676–680.

[5]delrio,R.and Gr′ebert,B.,Inverse spectral results for AKNS systems with partial information on the potentials,Math.Phys.Anal.Geom.,4(3),2001,229–244.

[6]Gesztesy,F.and Simon,B.,Inverse spectral analysis with partial information on the potential,II.The case of discrete spectrum,Trans.Amer.Math.Soc.,352(6),2000,2765–2787.

[7]Wei,G.S.and Xu,H.K.,Inverse spectral problem with partial information given on the potential and norming constants,Amer.Math.Soc.Transl.,364(6),2012,3266–3288.

[8]Marchenko,V.A.,Some questions in the theory of one-dimensional linear differential operators of the second order,Trudy Moskov.Mat.Obshch.,1,1952,327–420(in Russian).

[9]Marchenko,V.A.,Sturm-Liouville Operators and Applications,Birkhauser,Basel,1986.

[10]Clark,S.and Gesztesy,F.,Weyl-Titchmarsh M-function asymptotics,local uniqueness results,trace formulas,and Borg-type theorems for Dirac operators,Trans.Amer.Math.Soc.,354(9),2002,3475–3534.

[11]Del Rio,R.,Gesztesy,F.and Simon,B.,Inverse spectral analysis with partial information on the potential,III.Updating boundary conditions,Internat.Math.Res.Notices,15,1997,751–758.

[12]Gesztesy,F.and Simon B.,Inverse spectral analysis with partial information on the potential,I.The case of an a.c.component in the spectrum,Helv.Phys.Acta,70,1997,66–71.

[13]Levitan,B.M.and Sargsjan,I.S.,Introduction to spectral theory:Selfadjoint ordinary differential operators,Translations of Mathematical Monographs,Amer.Math.Soc.,New York,39,1975,25–34.

[14]Danielyan,A.A.,Levitan,B.M.and Khasanov,A.B.,Asymptotic behavior of Weyl-Titchmarshmfunction in the case of the Dirac system,Moscow Institute of Electromechanical Engineering,Translated from Matematicheskie Zametki,50(2),1991,77–88.

[15]Levinson,N.,Gap and Density Theorems,Amer.Math.Soc.,New York,1940.

[16]Levin,B.J.,Distribution of zeros of entire functions,Gosudarstv.Izdat.Tehn.-Teor.Lit.,Moscow,1956,(in Russian).

[17]Conway,J.B.,Functions of One Complex Variable,2nd ed.,Vol.I,Springer-Verlag,New York,1995.

[18]Gasymov,M.G.and Dˇzabiev,T.T.,Solution of the inverse problem by two spectra for the Dirac equation on a finite interval,Akad.Nauk Azerbaˇ?dˇzan.SSR Dokl.,22(7),1966,3–6.