Moments of L-Functions Attached to the Twist of Modular Form by Dirichlet Characters?
Guanghua JI Haiwei SUN
1 Introduction
An important problem in number theory is to study the moments of central values ofL-functions.Many authors considered this problem for several families ofL-functions(see[1,3,6,8,10,16–17]etc).Among them,the family of twistingL-functions has received much attention in recent years.The aim of this paper is to consider the moments ofL-functions attached to the twist of the modular form by Dirichlet characters.
Letf(z)be a holomorphic cusp form of weightκwith respect to the full modular groupSL2(Z).Moreover,we assume thatf(z)is a normalized eigenfunction for all Hecke operators.In this casef(z)has the following Fourier series expansion:
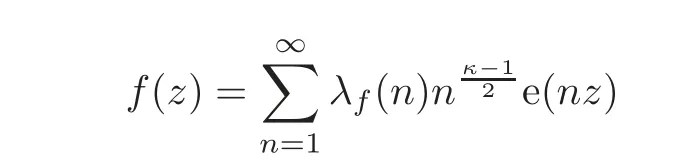
withλf(1)=1.
Such anfis called a holomorphic Hecke eigenform.Associated with each Hecke eigenformf,there exists anL-functionL(s,f),which is defined as

for Res>1.
Letqbe a positive integer andχbe a Dirichlet character moduloq.For Res>1,the automorphicL-functionsL(s,f?χ)are defined by
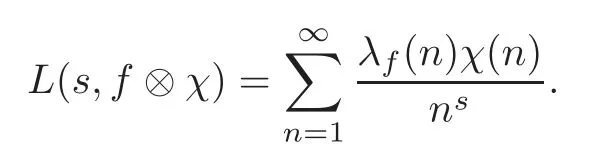
For any positive real numberk,we define
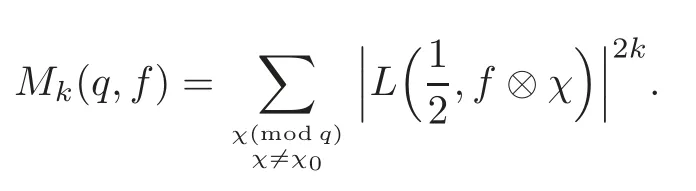
In this paper,we will estimate the upper and lower bounds ofMk(q,f).
Recently,Heath-Brown[6]proved that

fork=withn∈N,and under the GRH the estimate also holds for all positive real numbers 0 Using the method of[6],we hope to get the same upper bounds forMk(q,f)withunconditionally and 0 where(see Section 2 for the details) andσ≤1.In[13],Pi considered the last average for any real numberk(see Lemma 2.1).Using this lemma and the upper bounds of corresponding integrals ofMk(q,f),we will prove the following theorem. Theorem 1.1Forwith n∈N,we have and the estimate also holds for any real number0 To consider the lower bounds we will use the method of[15].In[15],Rudnick and Soundararajan considered the lower bounds ofMk(q)and proved that unconditionally for any rational numberk≥1,at least whenqis prime. In Section 3,we will establish different constitutions of the two sums and use the average estimates of Lemma 2.1,to prove the lower bound ofMk(q,f).But here we can not get unconditionally the lower bounds,since unconditionally the analytic continuation ofL(s,f?χ)kand the estimates of error terms are not good enough(see Section 3).So we assume that the GRH is ture forL(s,f?χ),and under this condition we can get the lower bounds for a more generalk. Theorem 1.2Let k be a fixed positive real number and q be any large prime,and under GRH for L(s,f?χ),we have It is known that for a primitiveχ,L(s,f?χ)admits analytic continuation to C as an entire function and satisfies the functional equation(see Proposition 14.20 of[7]) where is the completeL-function,τ(χ)is the Gauss sum,andηfis the eigenvalue offfor the operatorwith|ηf|=1.In addition,L(s,f?χ)has an Euler product of degree 2,which is for Res>1,whereαf(p),βf(p)∈C.For Res>1,we have where and For the definition of functiondk(·)we can refer to[5].If we assume the generalized Riemann hypothesis hold,then there exist no zeros forσ>,so that one can define a holomorphic extension of in the half-planeσ>. For the proof of Theorem 1.1,we will use the following integral: where the weight functionW(s)is defined by withδ>0 to be specified later.In addition toJ(σ,f?χ)we will also consider its average over non-principal characters In this section,we are mainly to estimate the upper bound ofJ(σ),i.e.,Lemma 2.6.Using this lemma we can prove Theorem 1.1. In[13],the author gave the estimate of the average(1.2),which we state as the following lemma whose proof is included for completeness. Lemma 2.1Let<σ≤1.For any real number k>0we have and ProofFirstly,we use the result of[18]to prove the following asymptotic formula: From[18]we know that if a multiplicative and nonnegative functionλ(n)satisfies the following three conditions: (i)For some constantτ>0, (ii)For some constantG>0 and any primep, (iii) then Hence we just need to show thatAf(n)satisfies the last three conditions. To check the condition(i),we apply(2.3)–(2.4)to see that where we use Deligne’s estimate(see[2]): From the following estimate(see[11]or[14]) and the partial summation formulae we have from which the condition(ii)follows.From(2.4)and Deligne’s estimate we have and now we can easily check that the condition(iii)is also true: Then from(2.6)–(2.8)we get the asymptotic formula(2.5).So now we just need to estimate the asymptotic formula.From the above estimates we can see that Now from(2.5)we get that with some constants 0 The following lemma is a convexity estimate(see[4]or[6]),which plays an important role in the proof. Lemma 2.2Let f and g be complex-valued functions which are regular in the strip{s∈C:α<σ<β},and continuous in the closed strip{s=σ+it:α≤σ≤β}.Let b and c be positive real numbers.Suppose that|f(s)|b|g(s)|cand|g(s)|tend to zero as t→∞,uniformly in{s=σ+it:α≤σ≤β}.Set Then,for α≤γ≤β, The following lemma gives the upper bounds ofJ(σ).In the proof,we use some properties and a mean value estimate ofL(s,f?χ),which are similar to the case ofL(s,χ).We just give the outline of the proof.For the details one can refer to Lemma 4 in[6]. Lemma 2.3Let≤σ≤1and1?σ≤γ≤σ.We have ProofBy Lemma 2.2,we get that if≤σ≤and 1?σ≤γ≤σ, By Hlder’s inequality,we get Firstly,we estimateJ(1?σ).Following the argument of Lemma 4 in[6],we can get the similar result with Note that the exponent ofqis 2k(2σ?1)but notk(2σ?1),becauseL(s,f?χ)is of degree 2 and the Stirling formula gives a doubled exponent. Then it is sufficient to prove the following inequality: From Lemma 4 of[6],we know that a mean value estimate is required.The following estimate(see[9])is the result corresponding to[12]for the fourth power moment ofL(s,χ),which is forindicates that only primitive characters are to be considered.From this mean value estimate we can prove(2.10)following the argument in[6].Therefore we prove that the result is true. In the following lemma,we will consider two other integrals.For the proof of the unconditional result of Theorem 1.1 we use forσ>Under the GRH we will employ forσ>Their averages over non-principal characters are Note that forH(σ),here we get an upper bound which is different from the result of Lemma 5 in[6].This improvement is the main point to get the unconditional result in our theorem.ForG(σ),the proof is exactly the same as Lemma 5 in[6].So we only give the proof forH(σ)here. Lemma 2.4LetUnder the GRH we have and unconditionally ProofWe only considerH(σ,f?χ).By Lemma 2.2 we have Therefore Forwe follow the argument in[6]and get that Now we estimate By Hlder’s inequality we have The first integral on the right is triviallyO(q6δ).Moreover, with certain coefficientsλf(n)n?.The argument then proceeds as[6],noting that It follows that Then from(2.11)we deduce that Now we consider the last integral.Let where Let be the average over non-principal characters.From Lemma 2.1 we can estimate the upper bound ofK(σ). Lemma 2.5LetWe have and ProofBy the definition we get where and Evaluating the sumS(m,n)we find that By Lemma 2.1 and observing that we can easily complete the lemma. From the above results,we can prove our main Lemma. Lemma 2.6Letwith some constant c>0.For1?σ0≤γ≤σ0we have ProofBy the definitions ofG(σ,f?χ)andH(σ,f?χ),we have under the GRH,and unconditionally.In view of Lemma 2.4 we have and respectively.However we also have and and therefore and in the two cases,respectively. Using Lemma 2.5,we find that under the GRH,since for 0 unconditionally. Finally we take then apply Lemma 2.3 withγ=and use(2.12)again,to deduce that under GRH and unconditionally We are now ready to choose the value ofδ.We writeck,1andck,2for the implied constants in the last two estimates respectively,and note that they depend only onk. Under the GRH,we take which ensure that and hence imply that Unconditionally,we take which ensure that and hence also imply that At last using Lemma 2.3,we can easily prove our result. Now following the argument in[6],we can extract the sumMk(q,f)from the integralJ(γ)and prove Theorem 1.1.Since|L(s,f?χ)|2kis subharmonic we have We now multiply byrand integrate for 0≤r≤Rto show that whereD=D(0,R)is the disc of radius ofRabout the origin,and dAis the measure of area. We take so that ifz∈DthenandIt follows that whence Since Meas(D)(logq)?2we now deduce from Lemma 2.6 that as required. In this section,we will give the lower bound ofMk(q,f).Letxbe a small power ofq,and set We will evaluate and show thatThen Theorem 1.2 follows from Hlder’s inequality: We start withS2.By Lemma 2.1 we getand thus Sincex Then using Lemma 2.1 we find thatS2φ(q)(logq)k2. We now turn toS1.If Re(s)>1,integration by parts gives whereX≥x.To deal with the sum in the second integration we use Perron’s formula and get forThen we shift the path of integration to Re(s)=σ1>0.SinceL(s,f?χ)khas no pole,we have where Note that under GRH we have where?is a positive number.Hence we have and If we takethen we conclude that under GRH Ifthen(3.1)furnishes an analytic continuation ofThus we have Therefore Obviously the main term is Then using the orthogonality relation for characters we conclude that By Hlder’s inequality we have and So we get Now we first estimate the contribution of the off-diagonal terms. Here we may writen=m+ql,whereThe contribution of these of f-diagonal terms is Therefore From Lemma 2.5,we know that At last takingX=qandx=we deduce that This proves the theorem. AcknowledgementThe authors would like to express their thanks to the referees for many useful suggestions and comments on the manuscript. [1]Conrey,J.B.,Farmer,D.,Keating,J.,et al.,Integral moments ofL-functions,Proc.London Math.Soc.,91,2005,33–104. [2]Deligne,P.,La conjecture de Weil,Inst.Hautes Etudes Sci.Pul.Math.,43,1974,29–39. [3]Diaconu,A.,Goldfeld,D.and Hof f stein,J.,Multiple Dirichlet series and moments of zeta andL-functions,Compositio Math.,139,2003,297–360. [4]Gabriel,R.M.,Some results concerning the integrals of modudi of regular functions along certain curves,J.London Math.Soc.,2,1927,112–117. [5]Heath-Brown,D.R.,Fractional moments of the Riemann zeta-function,J.London Math.Soc.,24(2),1981,65–78. [6]Heath-Brown,D.R.,Fractional moments of DirichletL-funtions,Acta Arith.,145,2010,397–409. [7]Iwaniec,H.and Kowalski,E.,Analytic Number Theory,Amer.Math.Soc.Colloquinum Publ.,53,Amer.Math.Soc.,Providence,RI,2004. [8]Ji,G.H.,Lower bounds for moments of automorphicL-functions over short intervals,Proc.Amer.Math.Soc.,137,2009,3569–3574. [9]Kamiya,Y.,Zero density estimates ofL-functions associated with cusp forms,Acta Arith.,85,1998,209–227. [10]Keating,J.P.and Snaith,N.C.,Random matrix theory andL-functions ats=,Comn.in Math.Phys.,214,2000,91–100. [11]Liu,J.Y.and Ye,Y.B.,Selbergs orthogonality conjecture for automorphicL-functions,Amer.J.Math.,127,2005,837–849. [12]Montgomery,H.L.,Topics in Multiplicative Number Theory,Lecture Notes in Mathematics,227,Springer-Verlag,Berlin,New York,1971. [13]Pi,Q.H.,Fractional moments of automorphicL-functions on Gl(m),Chin.Ann.Math.,32B(4),2011,631–642. [14]Rudnick,Z.and Sarnak,P.,Zeros of principalL-functions and Random matrix theory,Duke Math.J.,81,1996,269–322. [15]Rudnick,Z.and Soundararajan,K.,Lower bounds for moments ofL-functions,Proc.Natl.Acad.Sci.,102,2005,6837–6838. [16]Rudnick,Z.and Soundararajan,K.,Lower Bounds for Moments ofL-Functions:Symplectic and Orthogonal Examples,Multiple Dirichlet Series,Automorphic Forms,and Analytic Number Theorey,Proc.Symp.Pure Math.,75,Amer.Math.Soc.,Providence,RI,2006. [17]Soundararajan,K.and Young,M.P.,The second moment of quadratic twists of modularL-functions,J.Euro.Math.Soc.,12(5),2010,1097–1116. [18]Wirsing,E.,Das asymptotische verhalten von summen¨uber multiplikative funktionen II,Acta Math.Acad.Sci.Hungar.,18,1967,411–467.
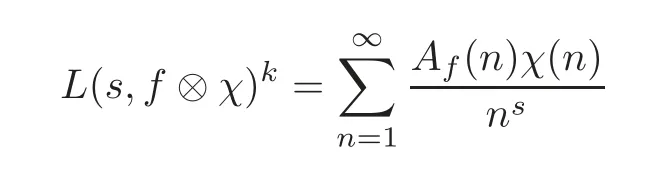
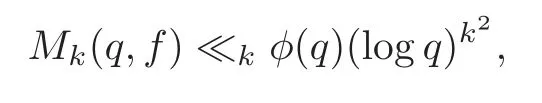
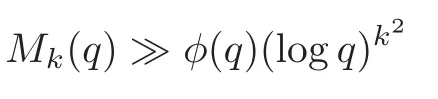
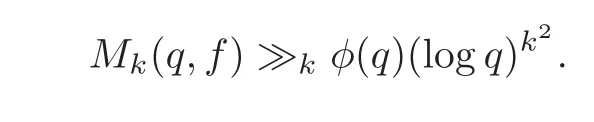
2 Proof of Theorem 1.1
2.1 Introduction
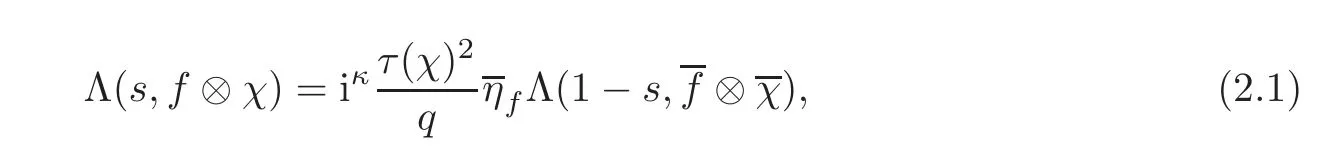
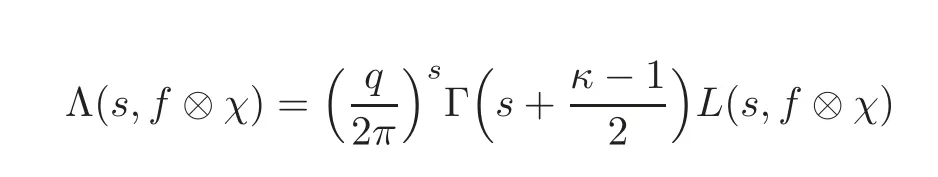
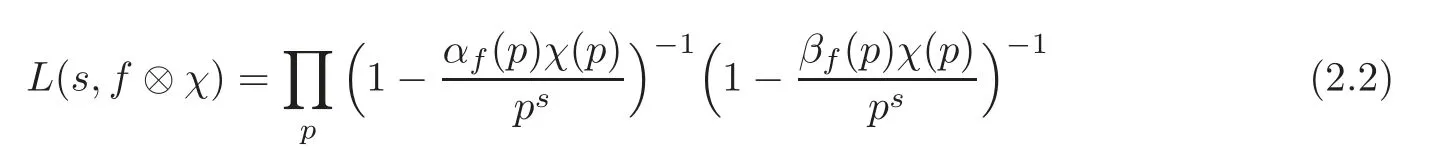
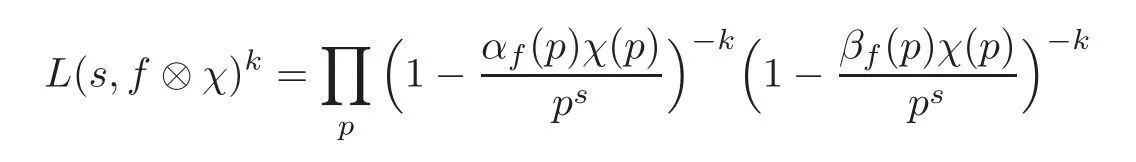
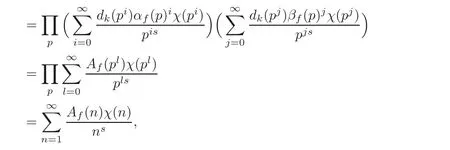
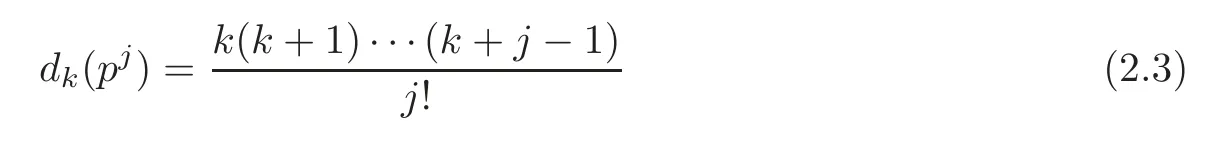
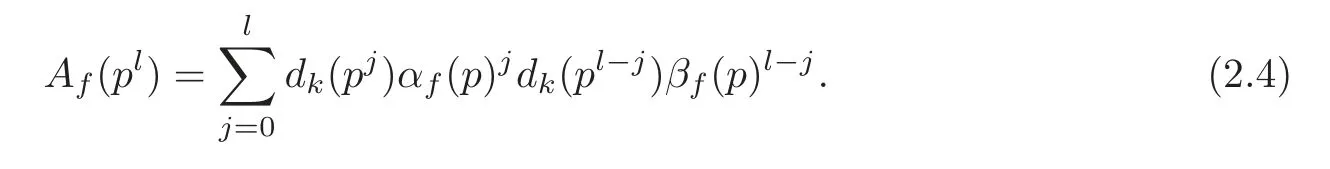
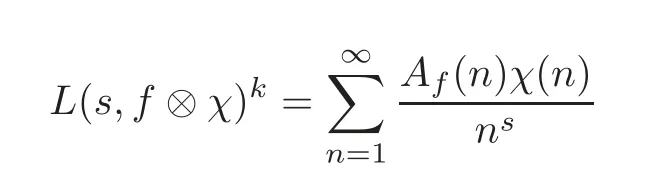
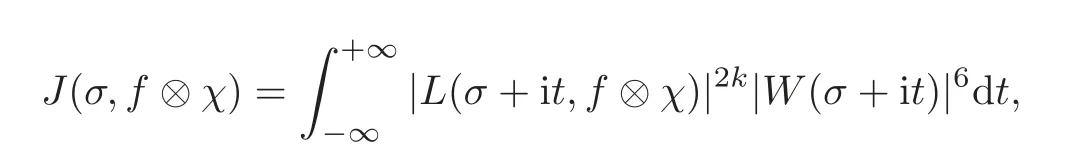
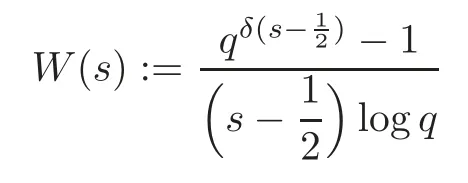
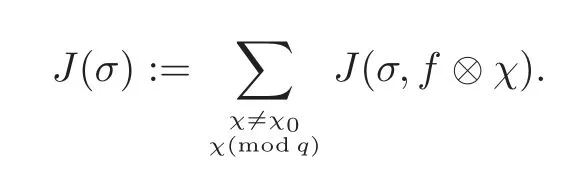
2.2 Necessary lemmas
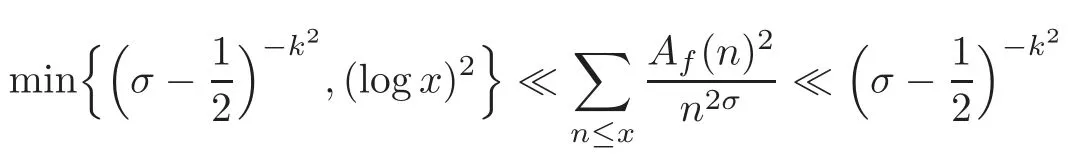
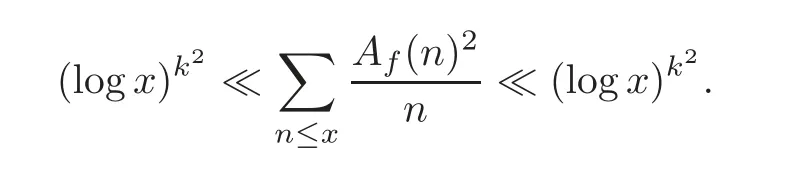
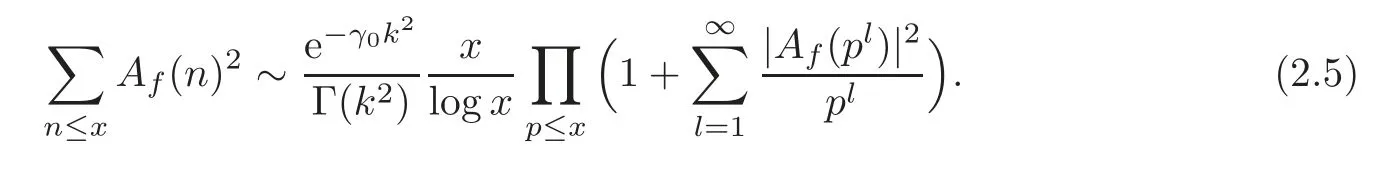
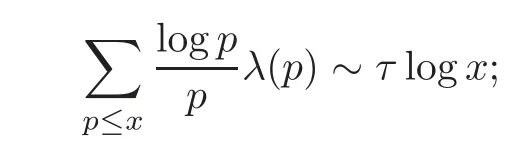
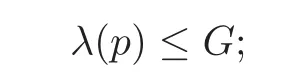
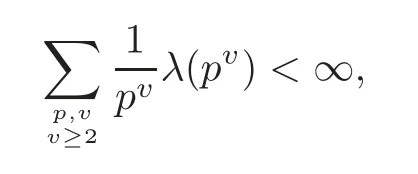
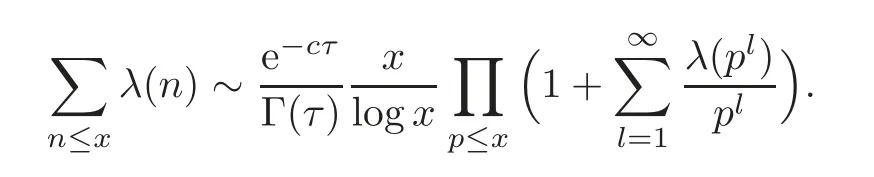
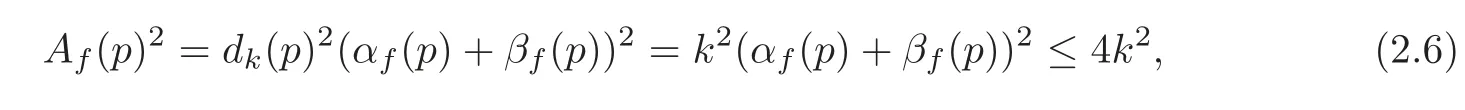
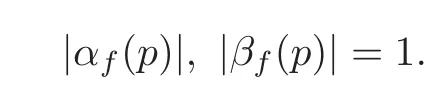
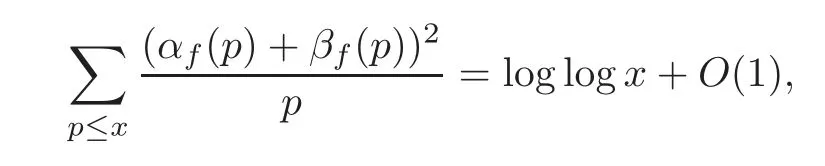
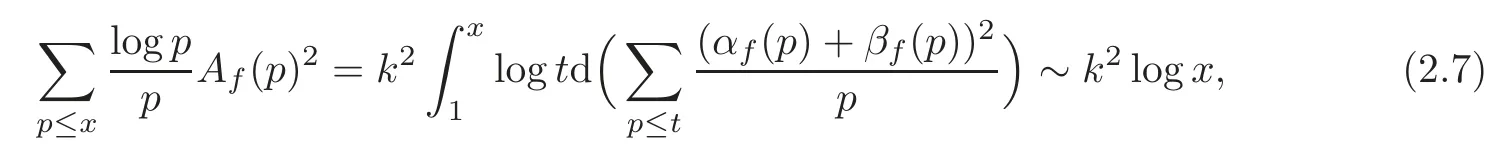
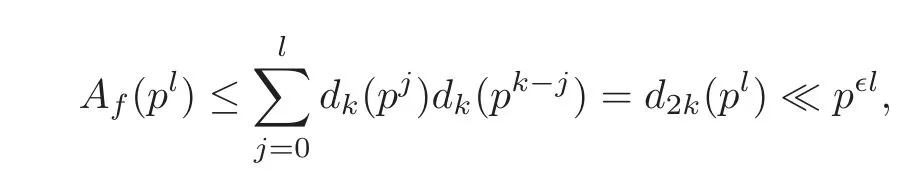
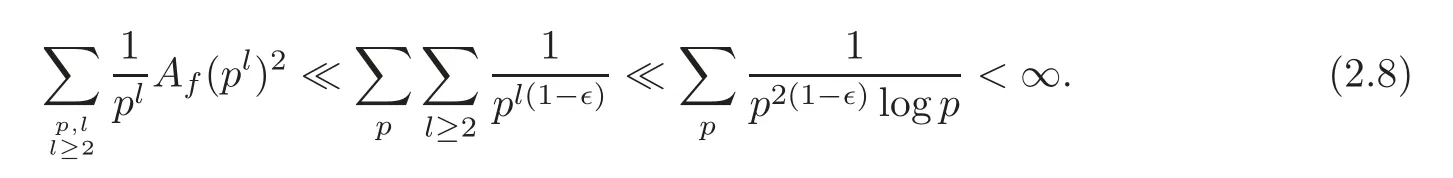
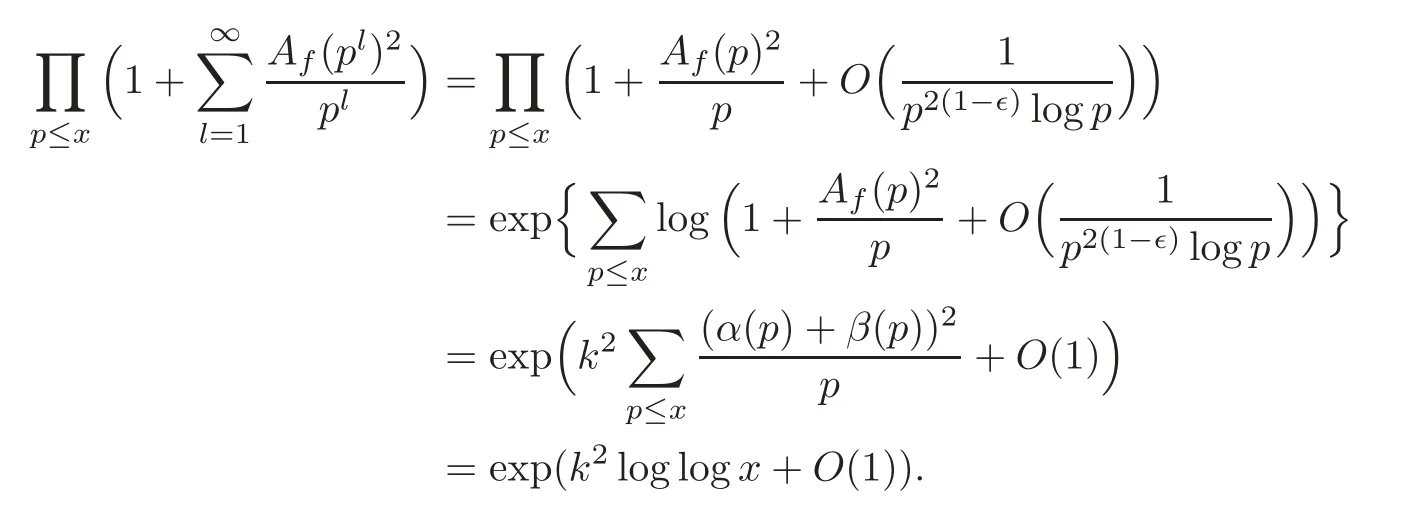
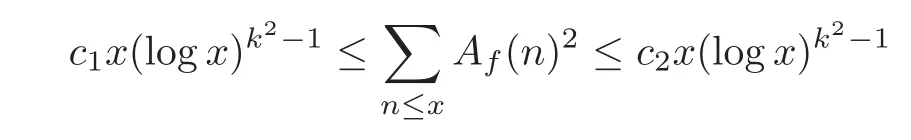
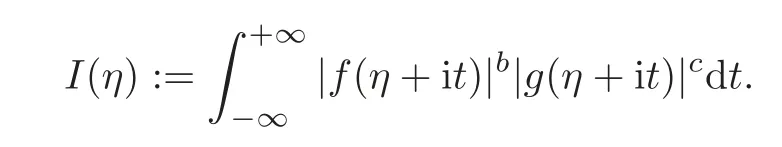
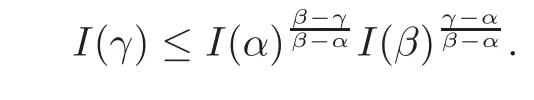
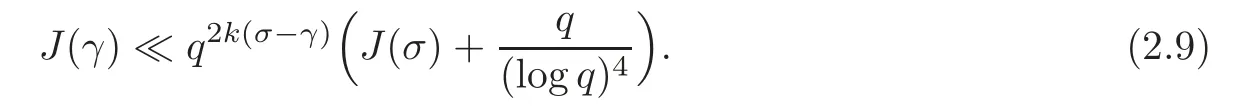
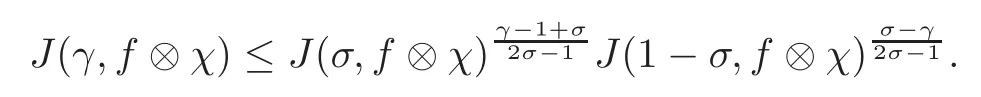
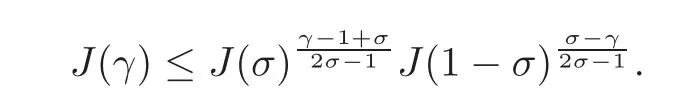
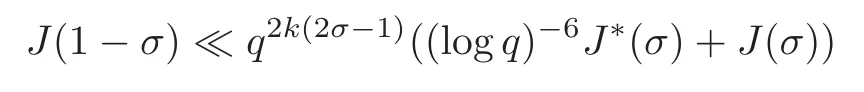
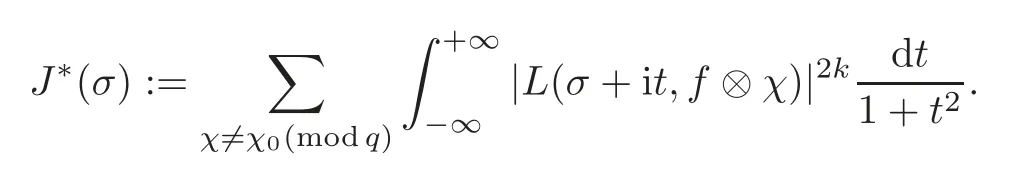

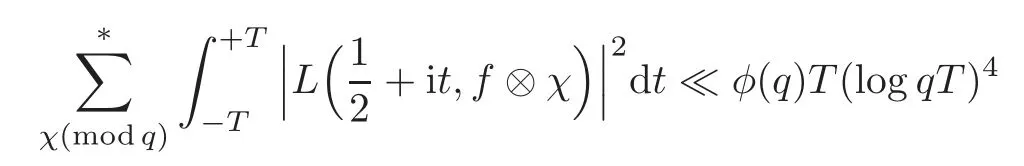
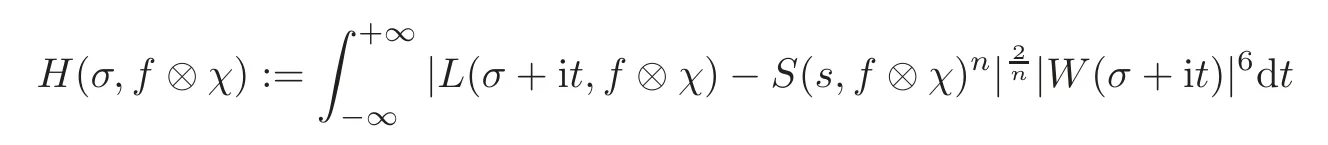
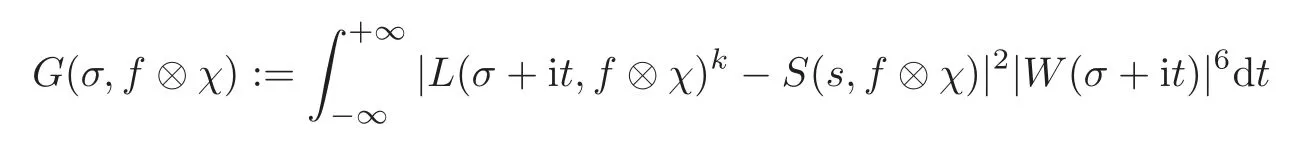
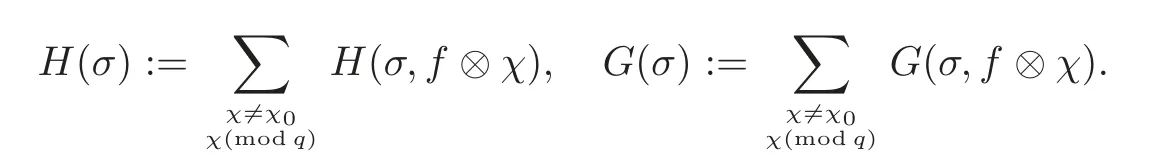
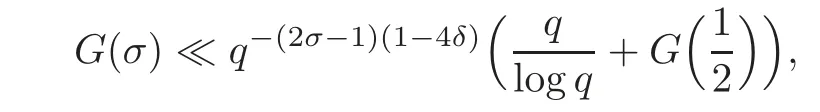
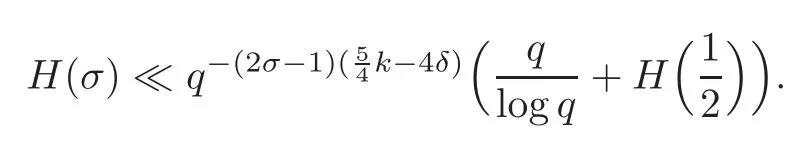
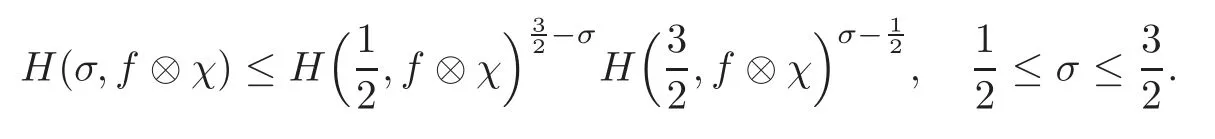
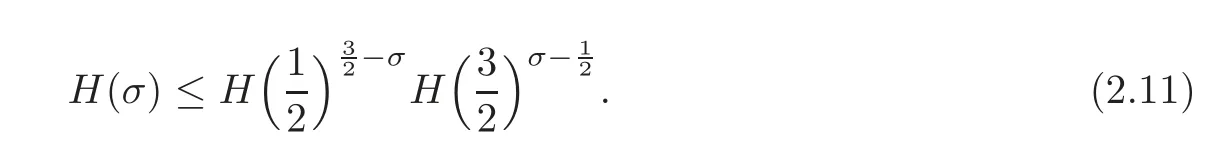
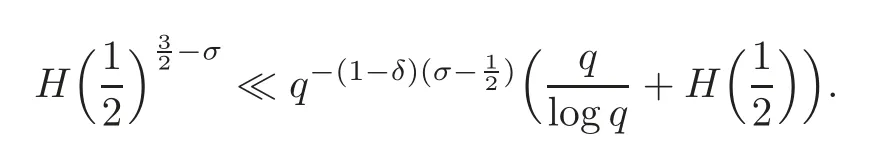
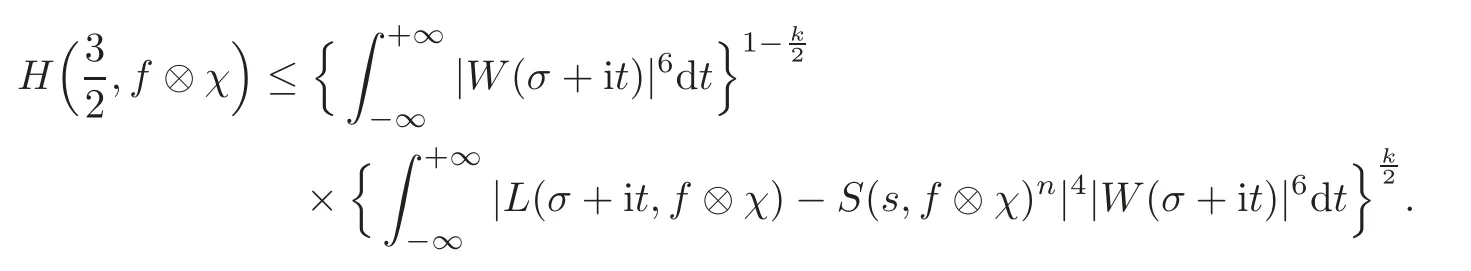
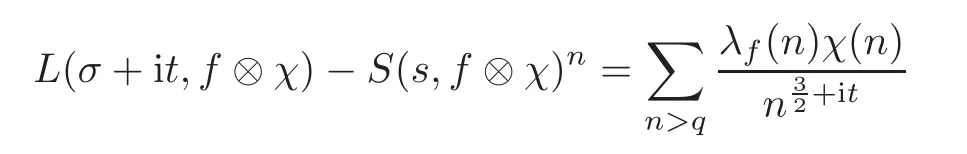
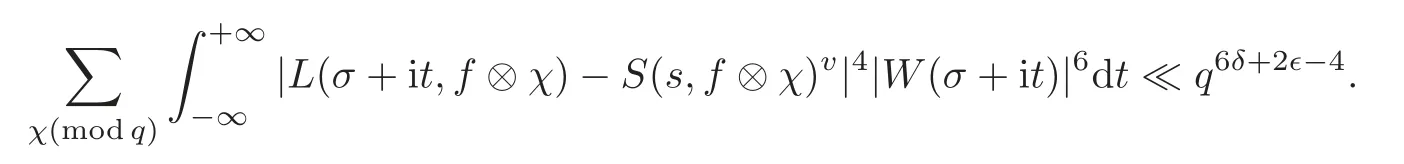
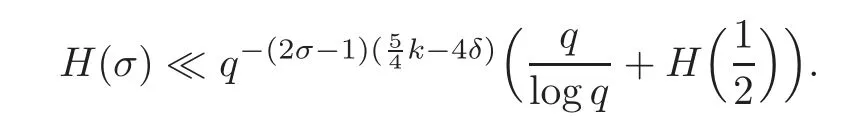
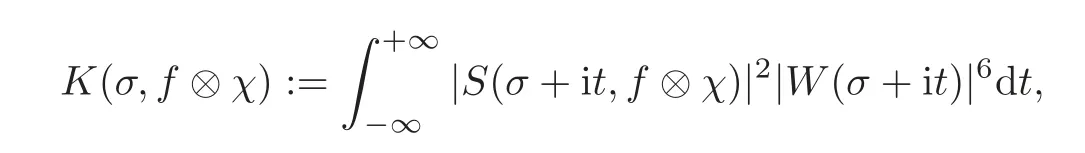
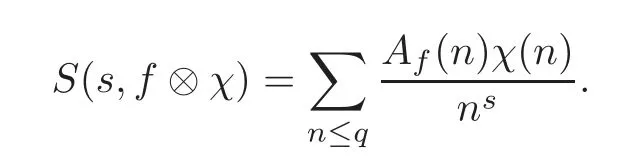
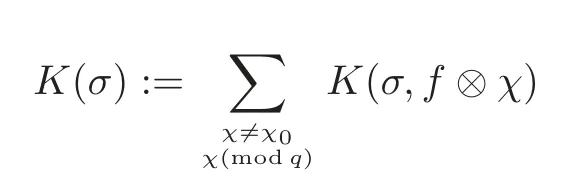
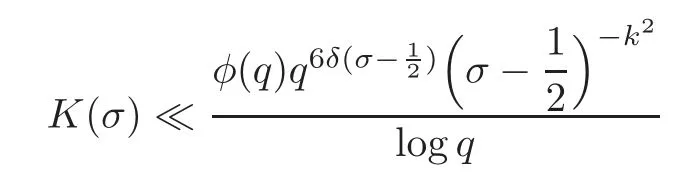

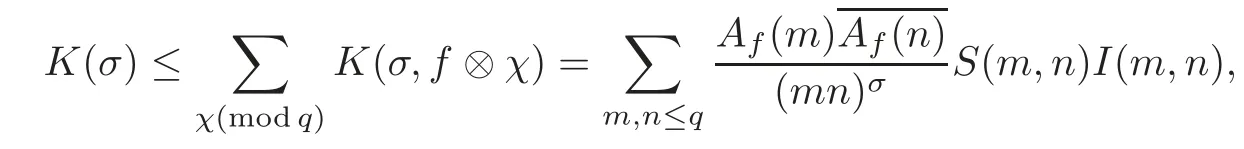
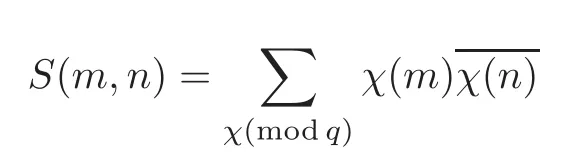
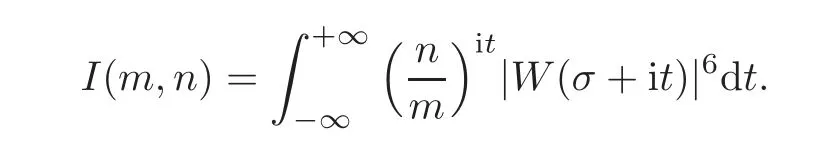
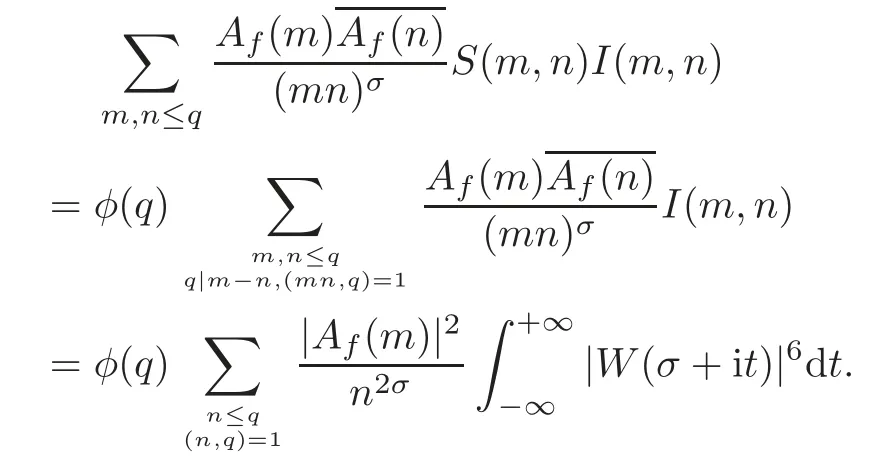
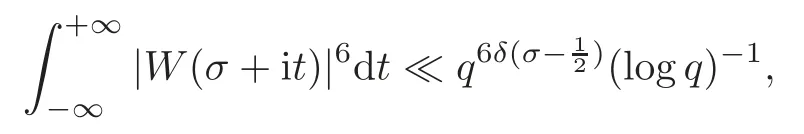
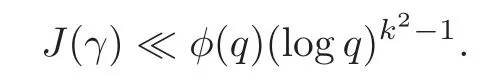
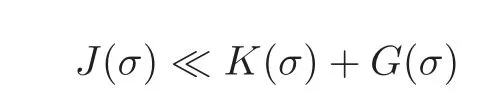
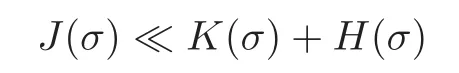
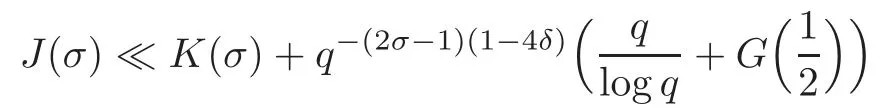
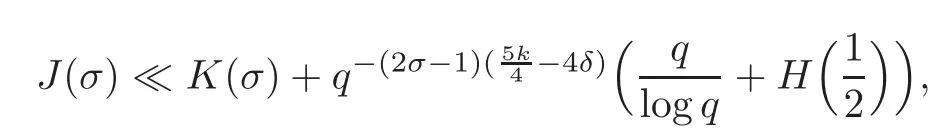
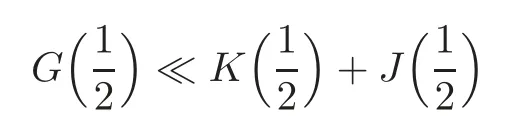
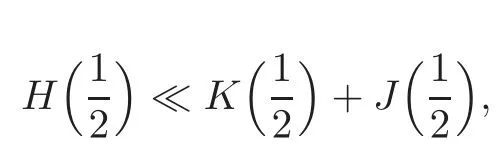
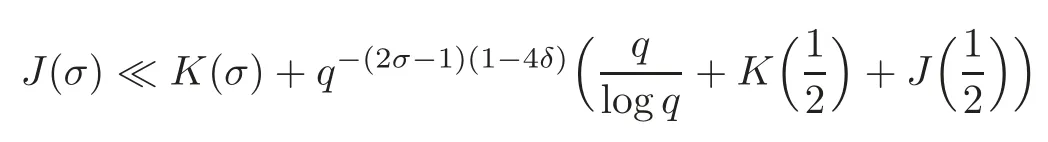
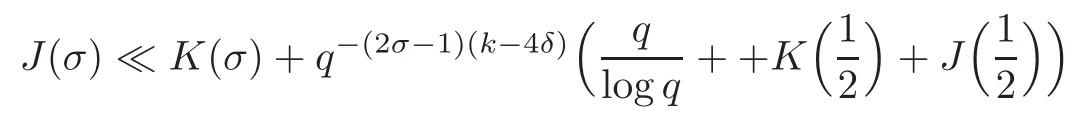

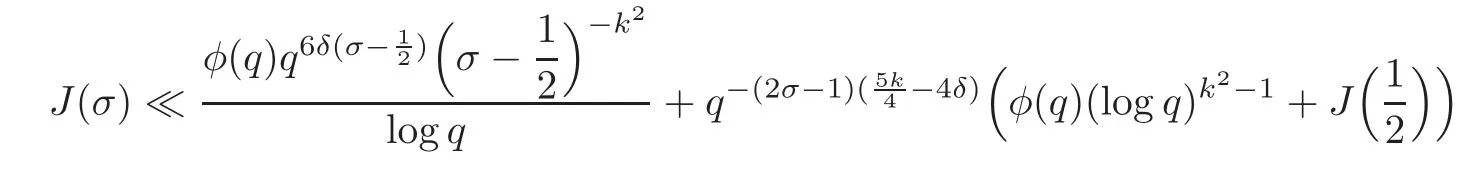
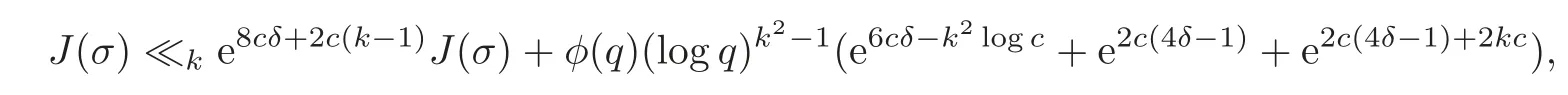
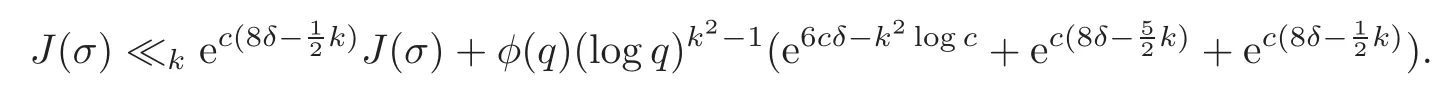
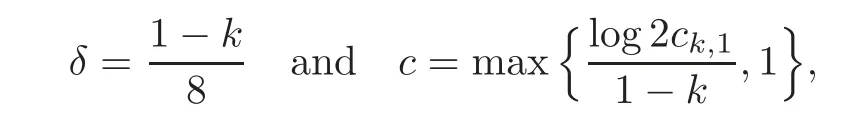
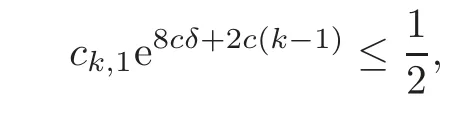
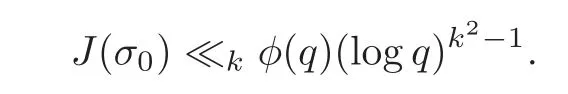

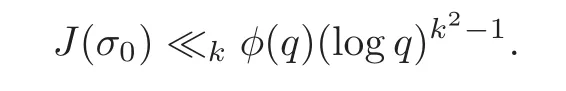
2.3 Proof of the theorem
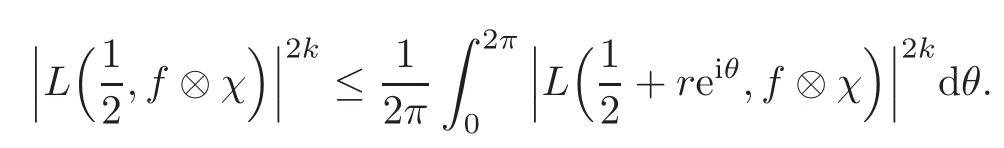
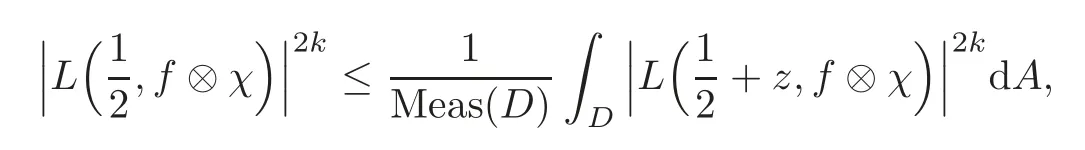

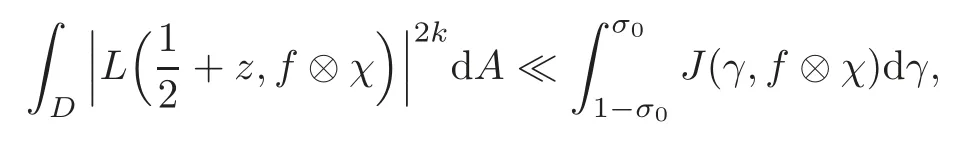
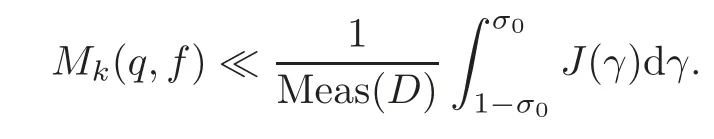
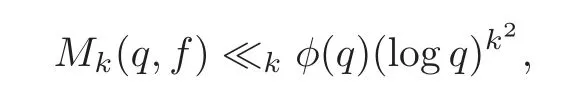
3 Proof of Theorem 1.2
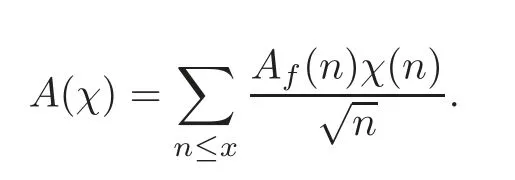
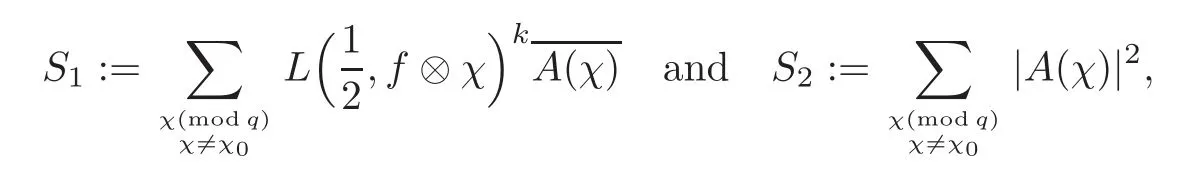
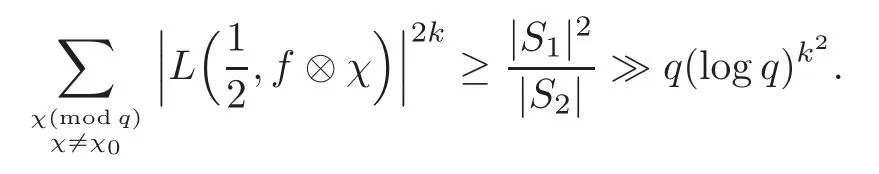
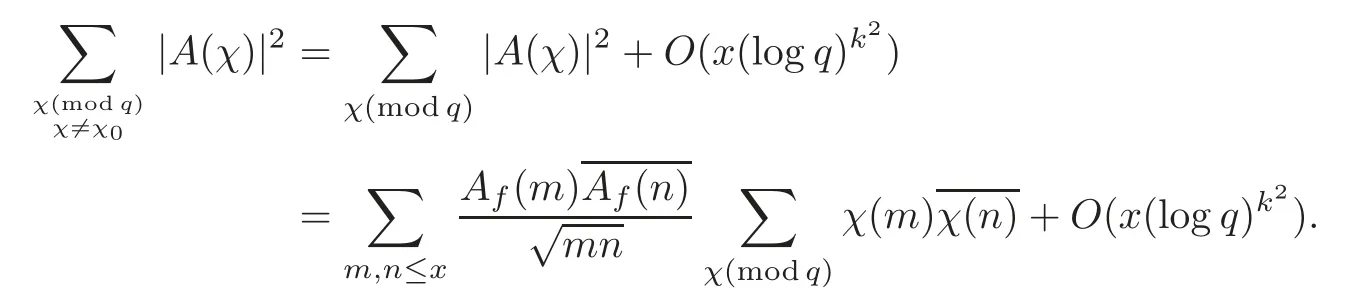
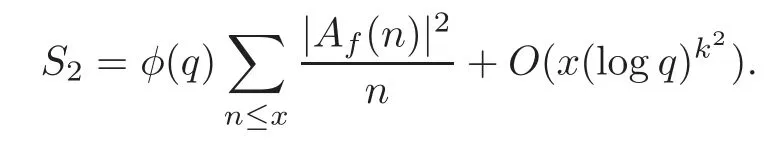
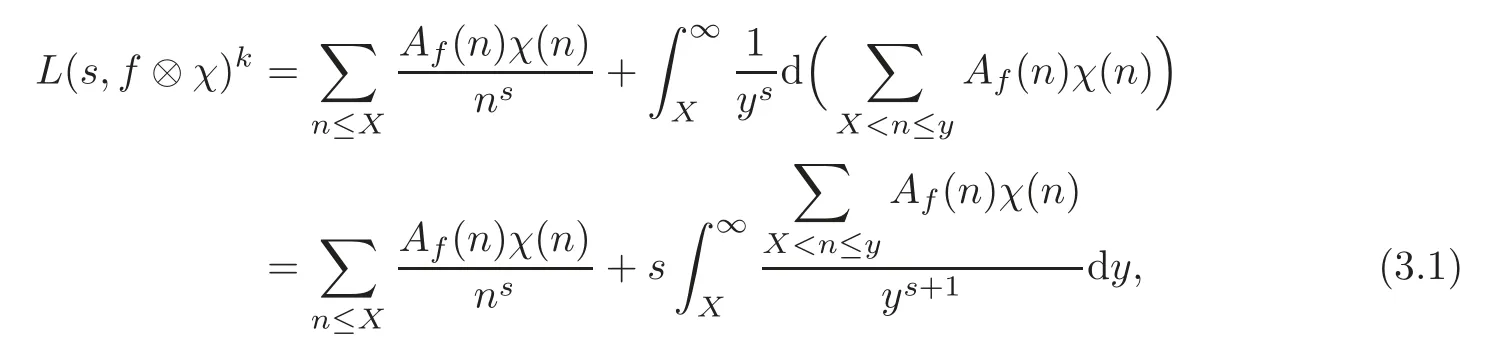
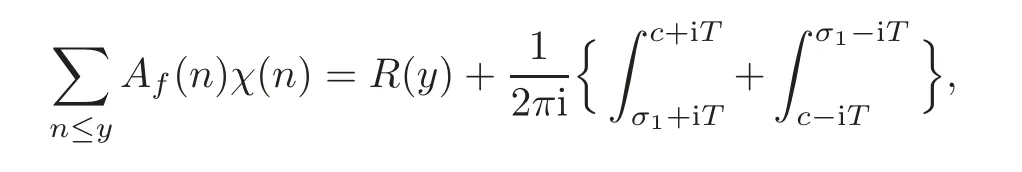
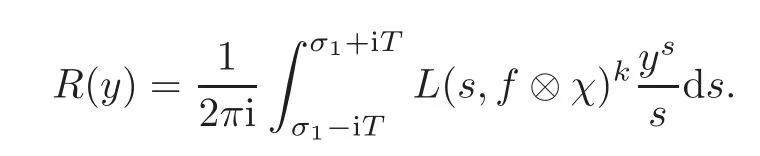
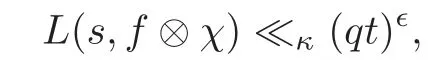
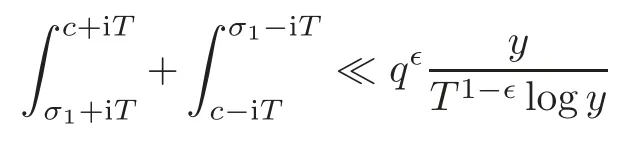
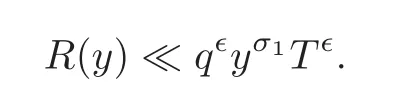
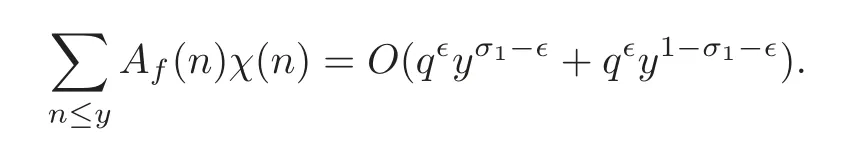

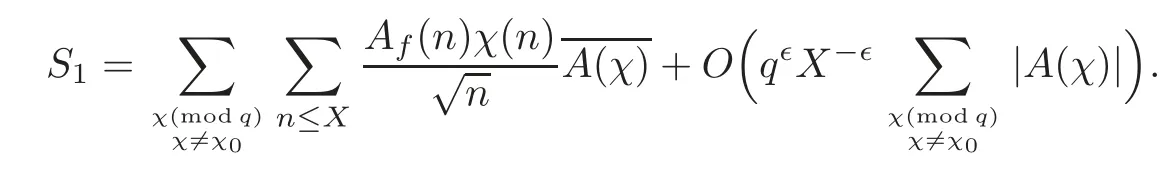
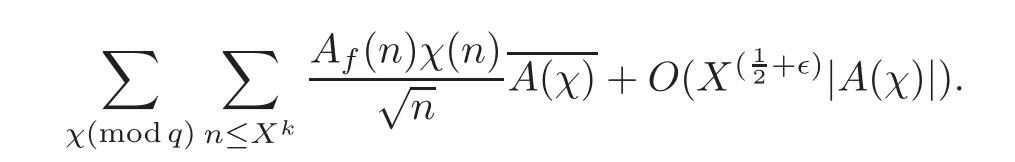
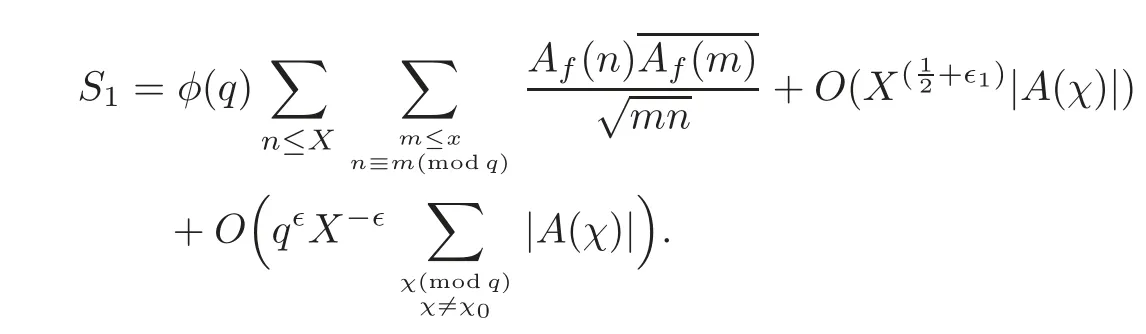
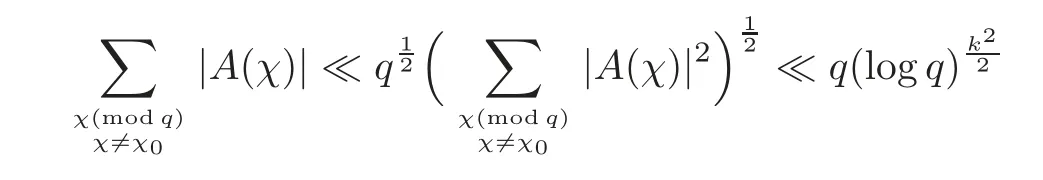
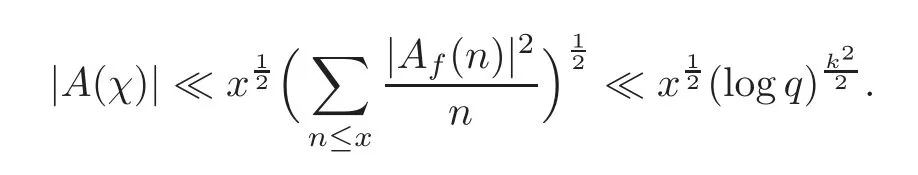
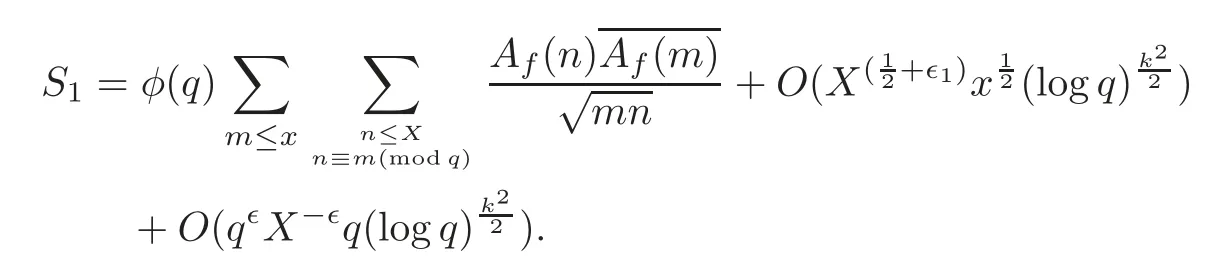
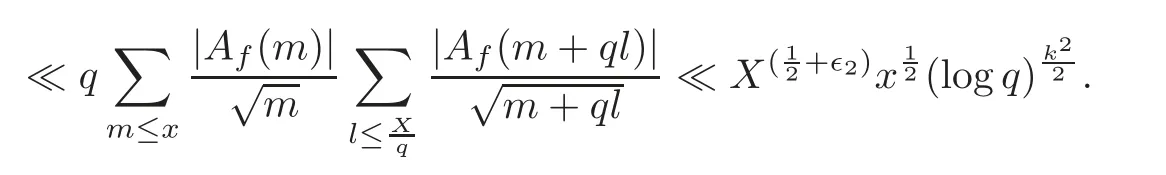
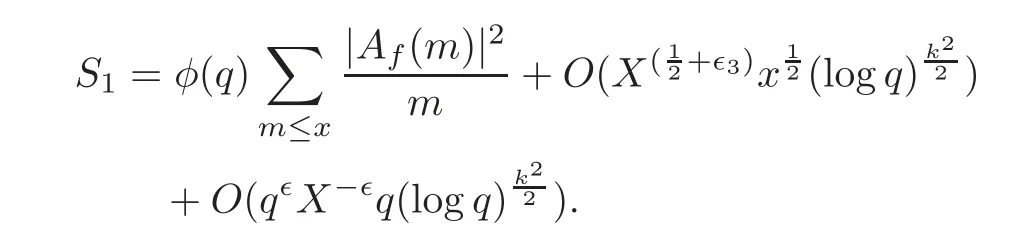

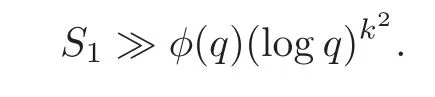
 Chinese Annals of Mathematics,Series B2015年2期
Chinese Annals of Mathematics,Series B2015年2期
