Derivations of the Even Part of Finite-Dimensional Simple Modular Lie Superalgebra M?
Lili MA Liangyun CHEN
1 Introduction
In this paper,we pay our main attention to finite-dimensional Lie superalgebras over a field of prime characteristic.As is well-known,the theory of Lie superalgebras over a field of characteristic zero(see[1–4])has experienced a vigorous development.For example,the classi fi cation by Kac of finite-dimensional simple Lie superalgebras over algebraically closed fields of characteristic zero was completely obtained(see[4]).However,that is not the case for modular Lie superalgebras,that is,Lie superalgebras of prime characteristic.The early work about modular Lie superalgebras was reported in[5].Recently,eight families of finitedimensional Cartan-type modular Lie superalgebrasX(m,n,t)were de fined and the derivation superalgebras ofX(m,n,t)were discussed,whereX=W,S,H,K,HO,KO,Ω and Γ(see[7–8,11,13–17]).The finite-dimensional simple modular Lie superalgebraMand its derivation superalgebra were investigated in[9].This paper is a continuation of[9].
Given a Lie superalgebraM=M⊕Mit is clear that the derivation superalgebra ofMis still a Lie superalgebra,denoted by Der(M)=Der(M)⊕De(M).An interesting question naturally arises:Whether the derivation algebra of Lie algebraMequals the even part of derivation superalgebra Der(M)or not,namely,Der(M=Der(MIn this paper,this question will be answered for the finite-dimensional simple modular Lie superalgebraMover a field of prime characteristic.
Let M denote the even part of the Lie superalgebraM.Since M is a Lie algebra,one may describe the derivation algebra Der(M)in a systematic way.However,in contrast to the case of Lie superalgebraM,one can not obtain directly the structures of Der(M),since M is neither transitive nor admissibly graded.[6,12]may inspire our work on modular Lie algebra M,the even part of the Lie superalgebraM,in which the even parts of Lie superalgebrasW,S,and Ω were discussed.
The organization of the rest of this paper is as follows.In Section 2,it is necessary to recall notions concerning Lie algebras,Lie superalgebras and the modular Lie superalgebraM.In Section 3,the generator sets of M are discussed in order to investigate the derivation algebra Der(M).In Section 4,the derivation algebra Der(M)is explicitly described by using the method of reduction on Z-gradations.
2 Preliminaries
Throughout,the ground field F is assumed to be of characteristicp>3 and F is not equal to its prime field Π.Let N be the set of positive integers and N0be the set of non-negative integers.Givenn∈N,letr=2n+2.Suppose thatμ1,···,μr?1∈F,such thatμ1=0,μj+μn+j=1,j=2,···,n+1.SetM={1,···,r?1}.Assume thatsi∈N0,i=1,···,r?1,ands=(s1+1,···,sr?1+1)∈Nr?1.We define a truncated polynomial algebra
such that
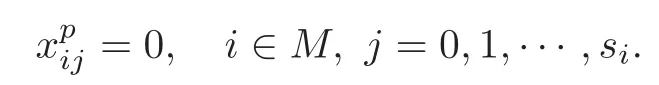
Fori∈M,we letπi=psi+1?1.Ifki∈N0such that 0≤ki≤πi,thenkican be uniquely expressed in ap-adic form as follows:
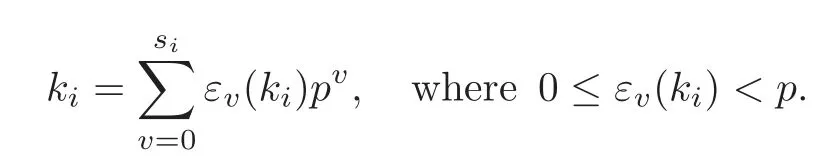
We setForandit is easy to verify that
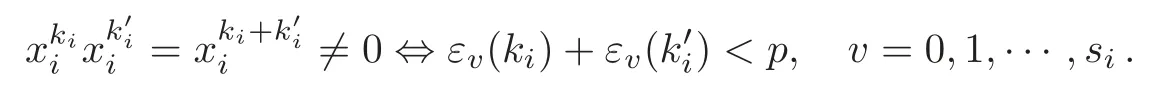
LetQ={(k1,···,kr?1)|0≤ki≤πi,i∈M}.Ifk=(k1,···,kr?1)∈Q,then letxk=
Givenq∈N{1}.Let Λ(q)be the Grassmann superalgebra over F inqvariablesξr+1,···,ξr+q.Denote the tensor product byr,q,s):=A?Λ(q).For convenience,(r,q,s)will be denoted byLet Z2:={,}denote the ring of integers modulo 2.Obviously,is an associative superalgebra with a Z2-gradation induced by the trivial Z2-gradation ofAand the natural Z2-gradation of Λ(q)as follows:
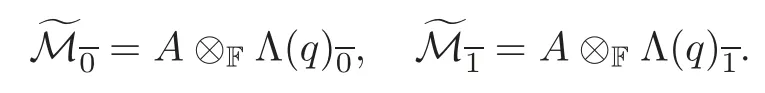
Iff∈A,g∈Λ(q),then we simply writef?gasfg.Fork∈{1,···,q},we set
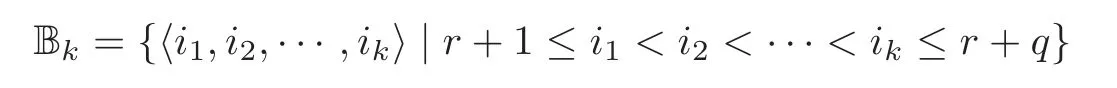
andwhere B0=?.Ifu=?i1,···,ik?∈Bk,we let|u|=k,{u}={i1,···,ik}andξu=ξi1···ξik.Put|?|=0 andξ?=1.Then{xkξu|k∈Q,u∈B(q)}is an F-basis of
IfLis a Lie superalgebra,thenh(L)denotes the set of all Z2-homogeneous elements ofL,i.e.,h(L)=L∪LIf|x|occurs in some expression in this paper,we always regardxas a Z2-homogeneous element and|x|as the Z2-degree ofx.
Sets=r+qandT={r+1,···,s}.PutM1={2,···,r?1}.Define=ifi∈M1;and=ifi∈T.
Let
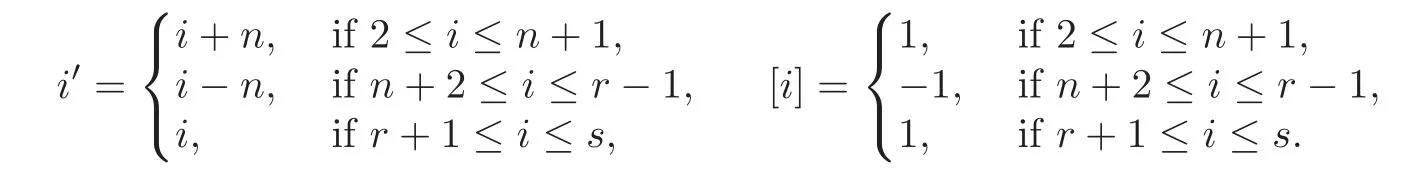
Putei=(δi1,···,δi(r?1)),i=1,···,r?1,and R=M∪T.Ifi∈R,then we letDibe the linear transformations ofsuch that
whereis the first nonzero number ofε0(ki),ε1(ki),···,εsi(ki).ThenDiis an even derivation offori∈M,andDjis an odd derivation forj∈T.Set
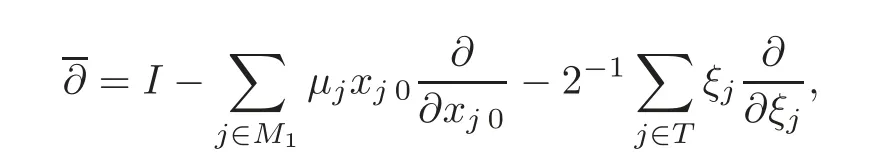
whereIis the identity mapping of
Forf∈h(),g∈we define a bilinear operation[,]insuch that
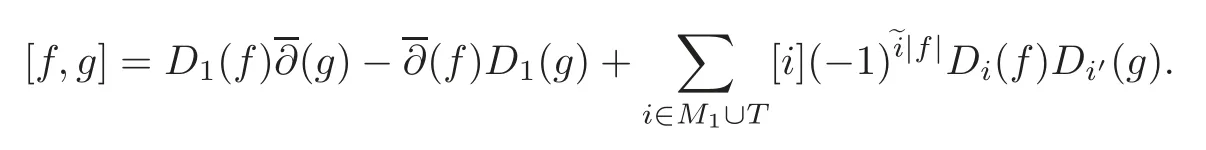
Thenbecomes a finite-dimensional Lie superalgebra for the operation[,]defined above. Leti∈M.Setπ=(π1,···,πr?1).DefineM=If 2?1q?n?20(modp),we obtain thatM=
Recall thatMis a Z2-graded Lie superalgebra:
Q,u∈
B(
q
)
,
=
α}.
Fori∈Z,we let
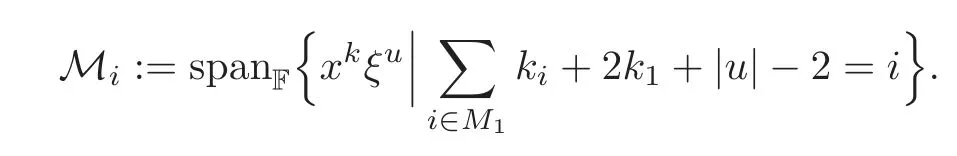
ThenwhereX={?2,?1,···,τ}andis a Z-graded Lie superalgebra.Letf∈M.Iff∈Mi,thenfis called a Z-homogeneous element andiis the Z-degree offwhich is denoted by zd(f).
We shall obtain the following fact.
The proof is straightforward and is therefore a simple statement.
Let B:=spanF{ξu|u∈B(q),|u|even},and then B=CM(M?1),the centralizer of M?1in M.In fact,for anyxkξu∈CM(M?1),from[xkξu,xi]=0,i∈M1,it follows that
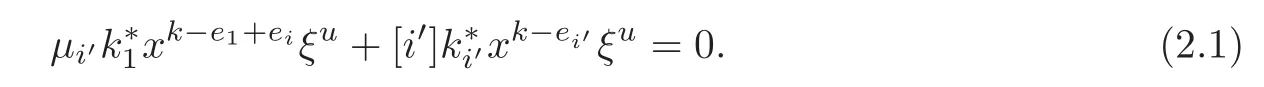
From(2.1),this shows that

According to(2.2)–(2.3),we have

Therefore,B is a Z-graded subalgebra of M.
Put Bi=B∩Miand
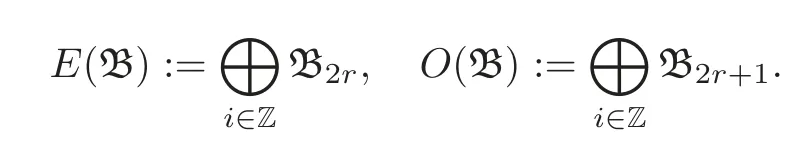
Since[O(B),O(B)]=0,O(B)is an ideal of M.It is easily seen that

whereM(q)?MsatisfyingM(q)=spanF{ξj|j∈T},andM(q)is the even part ofM(q).
Letbe a Z-graded Lie algebra.Recall thatGis called transitive(with respect to Z-gradation)provided that{x∈Gq|[x,G?1]=0}=0 for allq∈N0.We say thatGis admissibly graded ifCG(G?1)=G?r.
By the remarks above,M is neither transitive nor admissibly graded.In particular,M is not a simple Lie algebra.
3 Generator Sets of M
In this section,the generator sets of M,which will be applied to determine the derivation superalgebra of M,are given.
Put
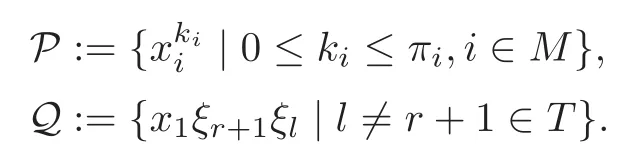
Foru,v∈B(q)withu∩v=?,defineu+vto bew∈B(q),such thatw=u∪v.If maxu Theorem 3.1Mis generated by P∪Q. ProofLetYbe the subalgebra of M generated byP∪Q.We first prove the following statements. (i)Assert that∈Y,ξu∈Yfor alli∈M,u∈B(q). In fact,by computation,we know that fori∈M1, If0,thenxiξr+1ξl∈Y.Otherwise,if=0,observing that we getxiξr+1ξl∈Y.It follows thatxiξr+1ξl∈Yfori∈M1. Clearly,fort∈Tandi∈M1, For|u|=2, wherei∈Mandl,t∈T. For|u|>2,we can writeu=v⊕w,wherev,w∈B(q),such that|w|=2.By the inductive hypothesis,we knowxiξv∈Yandxiξw∈Yfori∈M1. Case 1|v|0(modp).For0,we get For=0,we have Thus, Moreover, Case 2|v|≡0(modp).Forμi0,we obtain Forμi=0,we can get∈Y.Then It remains to show that In view ofxiξu∈Yfori∈M1,u∈B(q)and|u|even,we get as desired. Clearly, (iii)Assert that∈Yfor alli∈M1. For0,it follows thatIf=0,then Thus,x1xi∈Yfor alli∈M1. If 1?20,then If 1?2=0,then (iv)Assert thatfor alli∈M1. Using(ii)–(iii),it is clear that (v)Assert thatx1xiξu∈Yfor alli∈M1,u∈B(q). Case 1|u|1(modp).For our purpose,by(i),we first show that Forμi1,we know Forμi=1,by(ii),we have Case 2|u|≡1(modp). Discussing just as in(iii),we obtainIt is easy to verify the following fact: (vi)Assert thatfor 0≤k1≤π1. For|u|≡2(modp),it follows that For|u|2(modp),k1<π1,we get Ifk1=π1,the following equation holds: For 2?1|u|?20(modp),it is easy to see thatSuppose that 2?1|u|?2≡0(modp),namely,|u|≡4(modp).In view of(iii)andfor|u|2,k1<π1,it follows that Letμi0(otherwise,0,the proof is similar).By virtue of(v),we get Then (vii)Let wherei≥2.Thenρi(k1,u)∈Y. Let us complete the proof of(vii)by induction oni.Using(vi),it is clear thatρ1(k1,u)∈Y. Fork1<π1,we show thatρi(k1,u)∈Yby the inductive hypothesis and(iv).In fact, Suppose thatk1=π1.We obtain Ifi+1?2?1|u|0(modp),thenρi(π,u)∈Y.Leti+1?2?1|u|≡0(modp),μi+10(otherwise,μi+1=0,the proof is similar and is therefore omitted).It is easy to verify the following equations: Now,we prove the theorem by using(i)–(vii).Letz:=xkξube any basis element of M.SetWe propose to prove thatxkξu∈Yby induction onlz.Forlz=0,it follows thatz=ρn+1(k1,u)∈Y.Letlz>0.Then there isi∈M1,such thatki<πi.By the assumption of induction,we have:=xk+eiξu∈Yandg:=xk?e1+ei∈Y.Thus, The induction is complete. In this section,we shall describe the structure of the derivation algebra of M.Since M is not a simple modular Lie algebra,we can not obtain the corresponding conclusion for a simple modular Lie superalgebraMdirectly.This observation motivates us to pay our attention to the gradation component of zero Z-degree.Then,using the generator sets of M which have been obtained in Section 3,we decompose the derivations of nonzero Z-degree and zero Z-degree.As the final results,the derivations of the even part for the simple modular Lie superalgebraMare investigated. Lemma 4.1Let ?∈Der(M),f∈M.If ?(xi)=?[f,xi]=0,?i∈M1,then Di(?(f))=0,?i∈M,that is,where au∈F,u∈B(q). ProofNoting that?(xi)=?[f,xi]=0,it yields that[?(f),xi]=0,?i∈M1.Thus, It follows thatD1(?(f))=0 andDi(?(f))=[i][?(f),]=0,?i∈M1. An elementfof M is calledτ(i)-truncated if(f)=0,where Fori∈M,we define a linear mappingρi,such that wherexk+ei=0 fork+eiQ. From the definitions above,we can get the following result directly. Lemma 4.2The following statements hold: (i)If f∈Mis τ(i)-truncated,then Diρi(f)=f for all i∈M. (ii)Diρj=ρjDi,where i?=j∈M. Lemma 4.3Let ft1,···,ftk∈M,where t1,···,tk∈M.If fiis τ(i)-truncated,i=t1,···,tkand Di(fj)=Dj(fi),i,j=t1,···,tk∈M,then there exists f∈M,such that Di(f)=fi,i=t1,···,tk∈M. ProofInduction onk.Ifk=1,then letf=ρt1(ft1).In view of Lemma 4.2(i),we haveDt1(f)=Dt1ρt1(ft1)=ft1.Assume that there existsg∈M,such thatDi(g)=fi,i=t1,···,tk?1.Letf=g+ρtk(ftk?Dtk(g)).Fori=t1,···,tk?1,utilizing Lemma 4.2(ii)and the hypothesis of this lemma,we have Sinceftk?Dtk(g)isτ(tk)-truncated,by virtue of Lemma 4.2,we have Our assertion follows and this completes the proof. Lemma 4.4Suppose that ?∈Der(M).Let f1=?(1)and fi=[i]?()?[i]for i∈M1.Then there exists f∈M,such that Di(f)=fifor i∈M. ProofConsidering the definition ofτ(ti)-truncated,it is clear thatfi(i∈M)areτ(ti)-truncated.It remains to verify thatfi(i∈M)satisfy the condition of Lemma 4.3,that is,Di(fj)=Dj(fi),i,j∈M. By the assumption,we have Applying?to the equation[1,]=0,we obtain that that is,Di(f1)=D1(fi),i∈M1.Applying?to the equation=it follows that Moreover,Di(fj)=Dj(fi),i,j∈M1.Consequently,there existsf∈M,such thatDi(f)=fi,i∈M. Proposition 4.1Let ?∈Der(M).Then there exists f∈M,such that(??adf)(M?1)=0. ProofIt is easily seen that M?1=spanF{xi|i∈M1}.Letfibe defined as in Lemma 4.4.Then there existsf∈M,such thatDi(f)=fi,i∈M.Put?1:=??adf.It follows from(4.1)that wherei∈M1. Proposition 4.2Let ?∈Der(M).If ?|M?1=0,then ?=0,i∈M1. ProofUsing Proposition 4.1,we have?(xi)=0 fori∈M1,sincexi∈M?1.Applying?to the following equations respectively: wherej∈M1,we obtain that wherej∈M1.In view of Lemma 4.1,we knowwhereau∈F,u∈B(q). Applying?to the equationit follows that as desired. The following lemma is from[10,Proposition 8.4]. Lemma 4.5Letbe aZ-graded centerless Lie algebra,and letT?G0be atorus of G.If ?∈Der(G)is homogeneous ofZ-degree t,then there exists e∈Gt,such that(??ade)|T=0. It is easily verified thatT:=spanF{x1}is a torus of M. Lemma 4.6Let ?∈Dert(M),and suppose that ?(M?1)=0.Then there exists g∈(CM(M?1))t,such that(??adg)|T=0. ProofRecall that Noting thatx1∈M0,we get[x1,M?1]?M?1.Thus,?(x1)∈CM(M?1).By Lemma 4.5,there ise∈Mt,such that(??ade)|T=0.Thus,?(x1)=[e,x1]∈(CM(M?1))t.Noticing that[x1,ξu]=(1?2?1|u|)ξu,then there exists an elementg∈(CM(M?1))t,such that?(x1)=[g,x1].Consequently,(??adg)|T=0. Theorem 4.1Let ?∈Dert(M),t0.Then there exists f∈M,such that ?=adf. ProofBy Proposition 4.1,there existsf?∈M,such that(??ad)(M?1)=0.In view of Lemma 4.6,there existsg∈(CM(M?1))t,such that(??ad?adg)|T=0.Recall thatT=spanF{x1},and it follows that(??adf??adg)(x1)=0. Set It is clear thatσ(M?1)=0.In the following,recall thatandQ={x1ξr+1ξl|lr+1∈T},and we proceed in several steps to show thatσ(P)=0,σ(Q)=0,respectively. First,it will be proved thatfor alli∈M,by induction onki.Forki=0,from 1∈M?2,σ(1)=0 holds.Using Proposition 4.2,we getσ()=0.Suppose thatki>0.Thenby the inductive hypothesis.Applyingσtowe obtain In view of Lemma 4.1,we haveforj∈M.Applyingσto it follows that(fori∈M1)from Next,we prove thatfor 0≤k1≤π1by induction onk1.To do that,we assert thatTo simplify the proof,we only verifyas the proof ofis similar.For this propose,we may assume thatwherek∈Q,u∈B(q).One may check thatby applyingσto.Similarly,applyingσtowe can obtain Forak,u0,it is easily verified thatApplyingσto the following equations: respectively,from Proposition 4.2,we have Moreover,the following equations hold by direct computations: Applyingσto the equationwe get Using(4.2),we may obtain by comparing coefficients thatThen?j∈M1.So far,we may assume that In the following,we will show thatσ(ξr+1ξl)=0,l∈T.Using Lemma 4.1,it follows thatDi(σ(ξr+1ξl))=0,i∈M.We may assume thatwhereau∈F,u∈B(q),and|u|is even. Noticing that zd(σ(ξr+1ξl))=t>0 or zd(σ(ξr+1ξl))=t (4.3)yields thatc∈F.Applyingσtowe obtain Assume thatk1>3.Applyingσto the following equations: respectively,we get For 2??(k1?1)?0(modp),by(4.7),it is clear thatholds.For 2??(k1?1)?≡0(modp),that is,(k1?1)?=2,we have 3?(k1?2)?0(modp).Using(4.6),we obtainTo sum up,holds. Now,let us prove thatσ(x1ξr+1ξl)=0,l∈T.Applyσto=[i]ξr+1ξland,ji∈M1.Using Lemma 4.1,we getM.Applyingσto we have,i∈M1.Noting that the following equation holds by a direct computation: we haveσ(x1ξr+1ξl)=0,l∈T.The proof is complete. Theorem 4.2Let ?∈Dert(M),t=0.Then there exists f∈M,such that where|v(u)|=2,0,i∈M1,au,bu∈F,and l∈T. ProofIn view of the proof of Theorem 4.1,there existsσ=??ad?adg,where∈M,g∈CM(M?1),such thatσ(M?1)=0,σ(T)=0. We obtain the following results: Set Applyingσtowe obtain Forak,u0,by(4.8)–(4.9),we haveApplyingσto and we get Applyingσtoit follows that Using(4.10)–(4.11),we have Applyingσtowe get Applyingσtoit follows that Moreover, It is easily verified that each termis generated by somefm∈M andx1ξr+1ξl.Consequently,combining(4.12)–(4.14),we have whereau,bu,cu,du∈F,fm(u),fn(u)∈M. Let whereau,bu∈F. Noticing that the following equations hold by Theorem 3.1: we have Δ=0.Hence,there existsf∈M,such that where|v(u)|=2,i∈M1,l∈Tandau,bu∈F. Theorem 4.3 where i∈M1,l∈T,and|v|=2. ProofThis is a direct consequence of Theorems 4.1–4.2. Remark 4.1Now we can answer the question mentioned in the introduction for the simple modular Lie superalgebraM.By Theorem 4.3 and[9,Theorem 3],it is easy to see that the derivation algebra of the even part ofMdoes not equal the even part of the derivation superalgebra ofM,that is,Der(M)Der(M) AcknowledgementThe authors thank the referees for their careful reading and helpful suggestions. [1]Celousov,M.J.,Derivations of Lie algebras of Cartan-type(in Russian),Izv.Vyss.Uchebn.Zaved.Math.,98(7),1970,126–134. [2]Eldugue,A.,Lie superalgebras with semisimple even part,J.Algebra,183,1996,649–663. [3]Kac,V.G.,Classification of infinite-dimensional simple linearly compact Lie super-algebras,Adv.Math.,139(1),1998,1–55. [4]Kac,V.G.,Lie superalgebras,Adv.Math.,26(1),1977,8–96. [5]Kochetkov,Y.and Leites,D.,Simple Lie algebras in characteristic 2 recovered from superalgebras and on the notion of a simple finite group,Contemp.Math.,131,1992,59–67. [6]Liu,W.D.and Zhang,Y.Z.,Derivations of the even parts for modular Lie superalgebras of Cartan typeWandS,Internat.J.Algebra Comput.,17(4),2007,661–714. [7]Liu,W.D.,Zhang,Y.Z.and Wang,X.L.,The derivation algebra of the Cartan-type Lie superalgebraHO,J.Algebra,273,2004,176–205. [8]Ma,F.M.and Zhang,Q.C.,Derivation algebra of modular Lie superalgebraKof Cartan-type,J.Math.(PRC),20(4),2000,431–435. [9]Ma,L.L.,Chen,L.Y.and Zhang,Y.Z.,Finite-dimensional simple modular Lie superalgebraM,Front.Math.China,8(2),2013,411–441. [10]Strade,H.and Farnsteiner,R.,Modular Lie algebras and their representations,Monographs and Textbooks in Pure and Applied Math.,116,Marcel Dekker Inc.,New York,1988. [11]Wang,Y.and Zhang,Y.Z.,Derivation algebra Der(H)and central extensions of Lie superalgebras,Comm.Algebra,32(10),2004,4117–4131. [12]Wei,Z.and Zhang,Y.Z.,Derivations for even part of finite-dimensional modular Lie superalgebra?Ω,Front.Math.China,7(6),2012,1169–1194. [13]Xu,X.N.,Zhang,Y.Z.and Chen,L.Y.,The finite-dimensional modular Lie superalgebra Γ,Algebra Colloq.,17(3),2010,525–540. [14]Zhang,Q.C.and Zhang,Y.Z.,Derivation algebras of modular Lie superalgebrasWandSof Cartan-type,Acta Math.Sci.,20(1),2000,137–144. [15]Zhang,Y.Z.and Fu,H.C.,Finite dimensional Hamiltonian Lie superalgebras,Comm.Algebra,30(6),2002,2651–2673. [16]Zhang,Y.Z.and Liu,W.D.,Modular Lie Superalgebras(in Chinese),Science Press,Beijing,2004. [17]Zhang,Y.Z.and Zhang,Q.C.,Finite-dimensional modular Lie superalgebra Ω,J.Algebra,321,2009,3601–3619.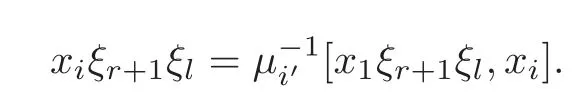
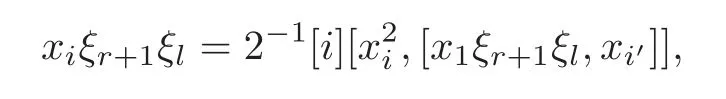
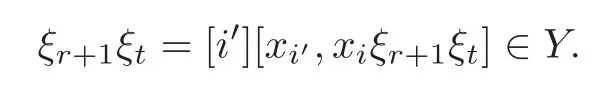

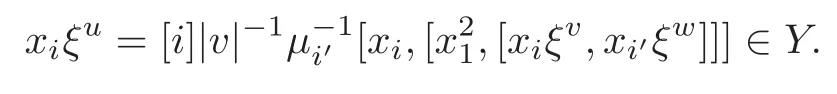
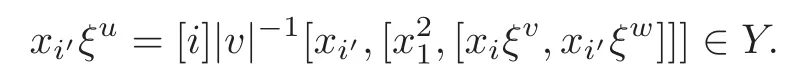
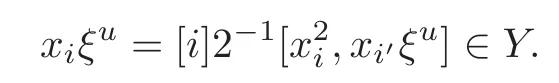
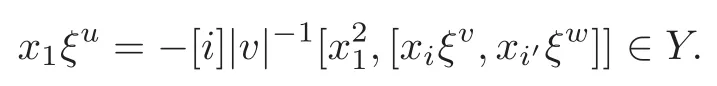
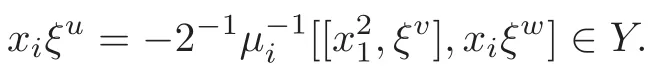
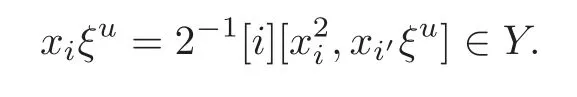
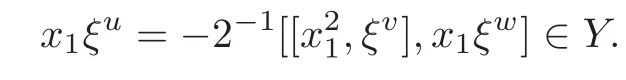
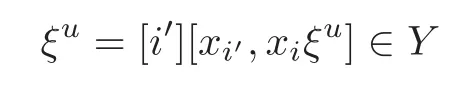
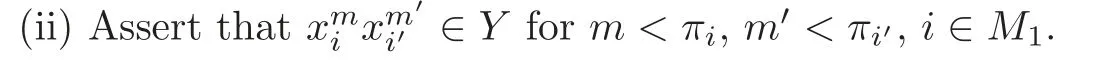
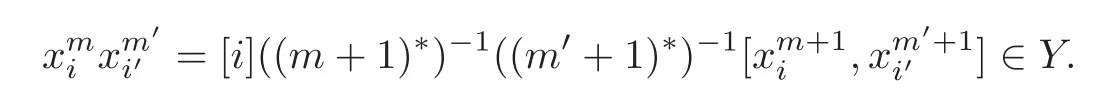
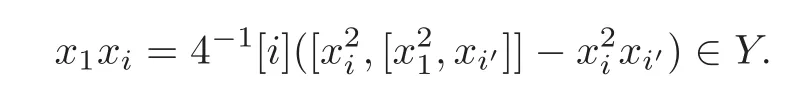
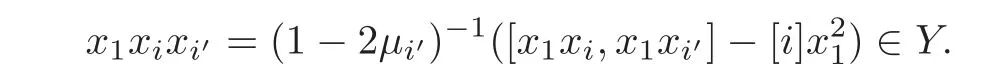
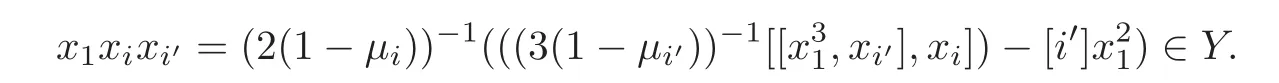
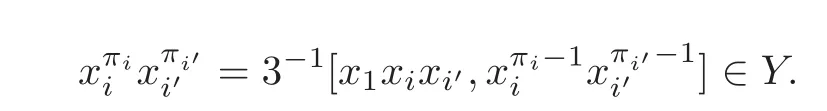
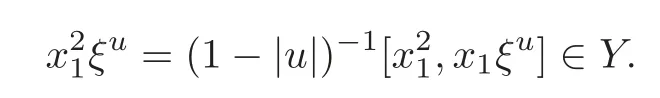
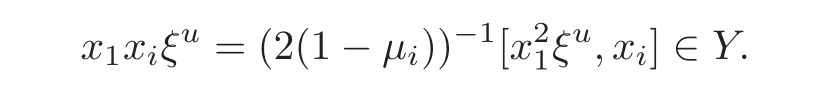
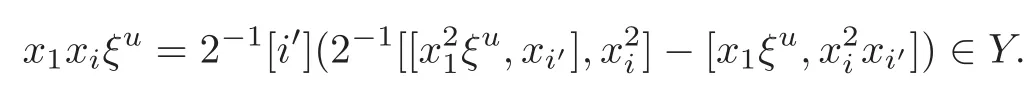
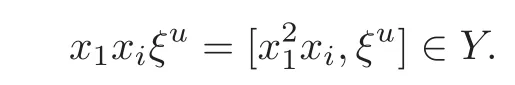
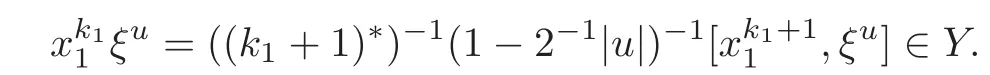
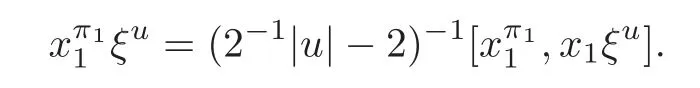
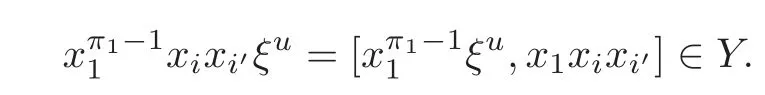
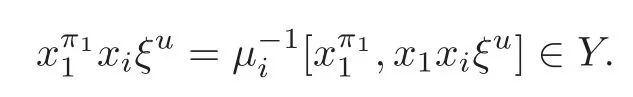
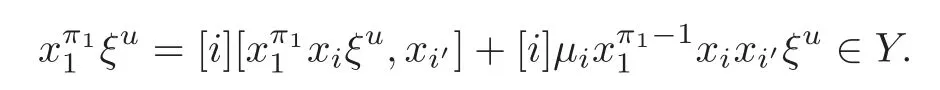
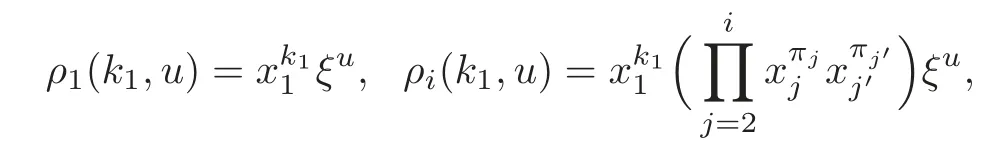
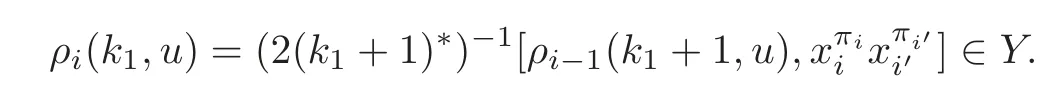
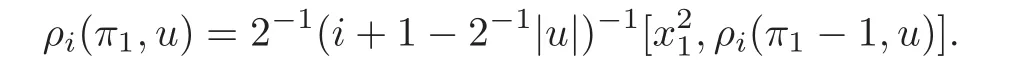
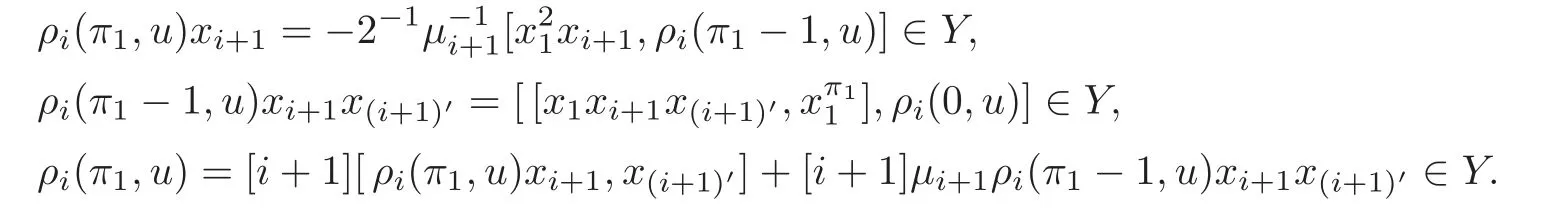
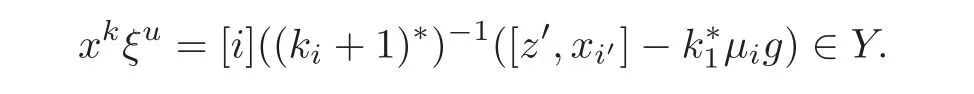
4 Derivations of M
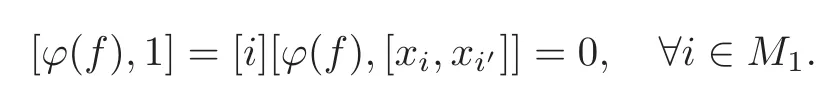
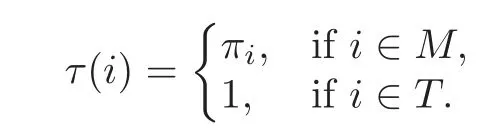
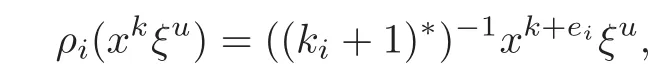
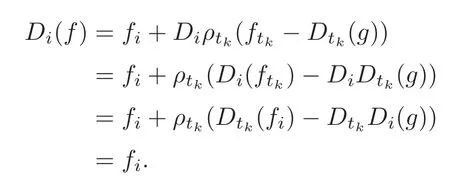
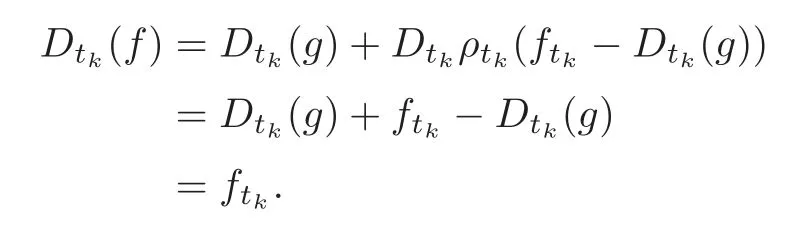

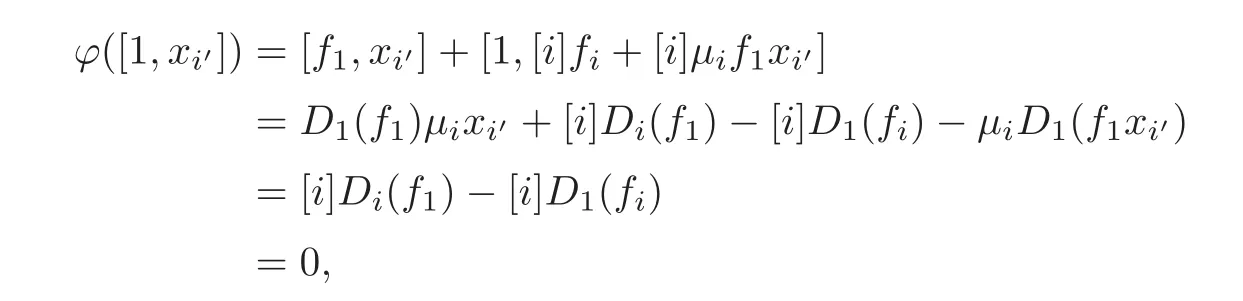
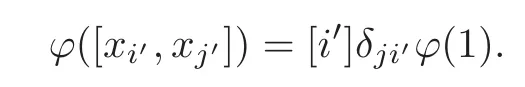
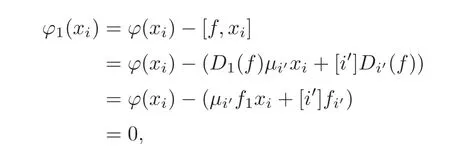
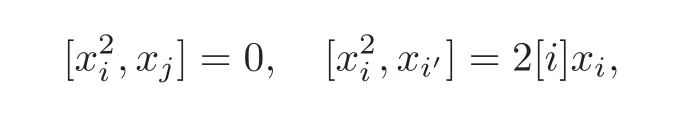
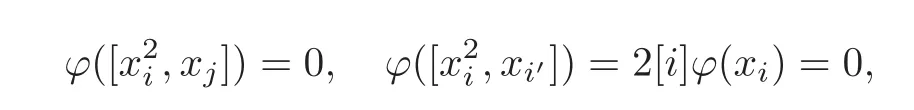
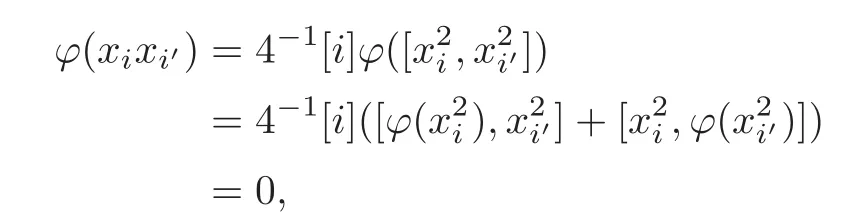
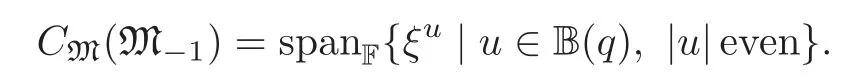
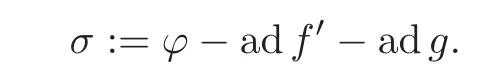
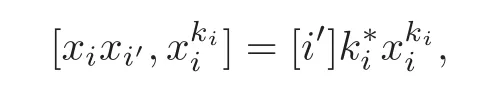

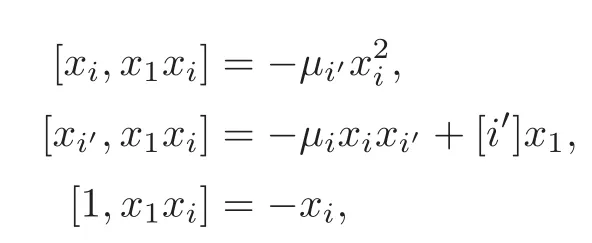
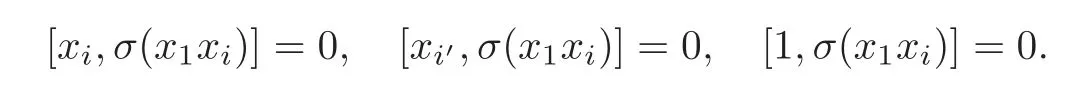
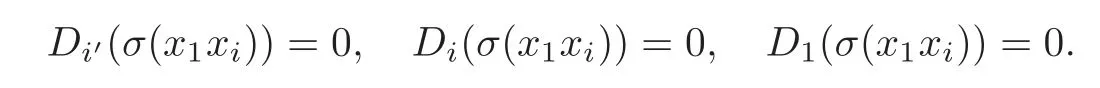


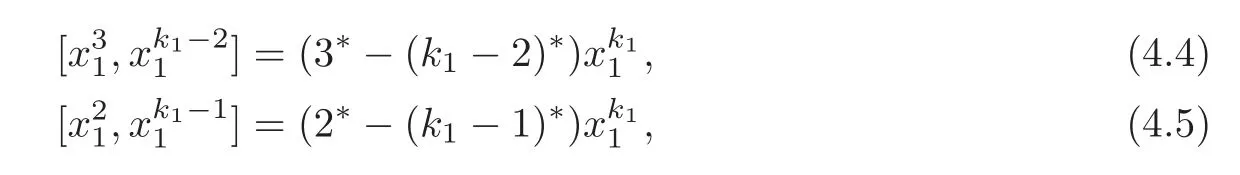
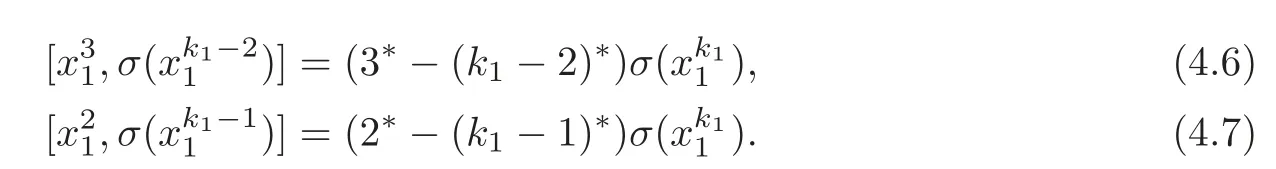
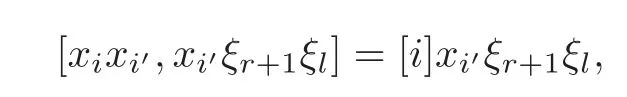
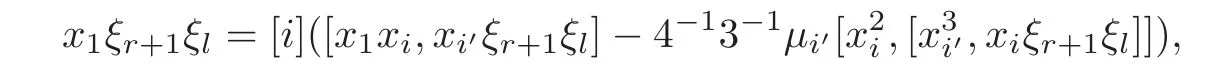
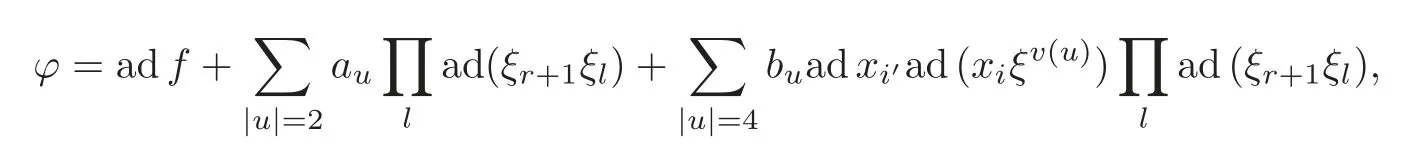
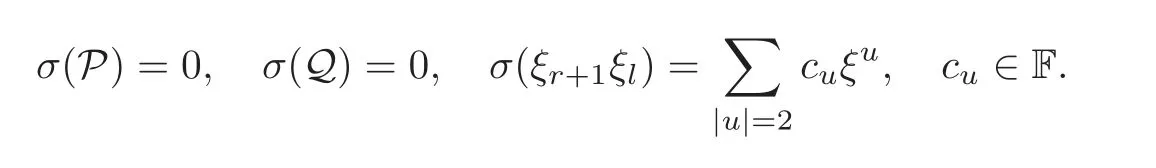
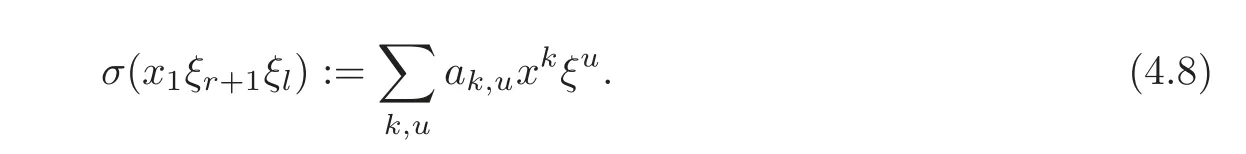
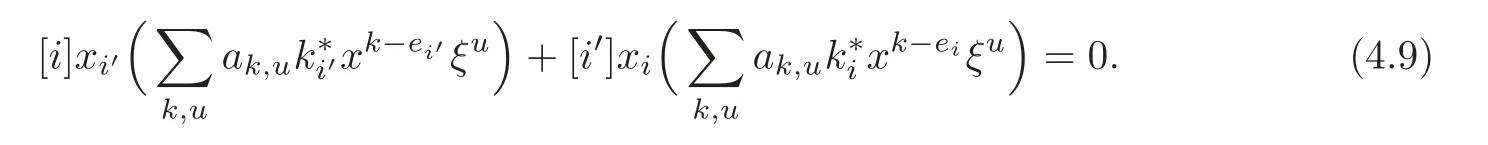
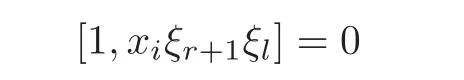
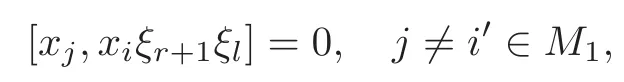
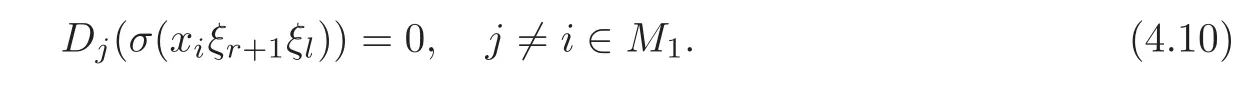
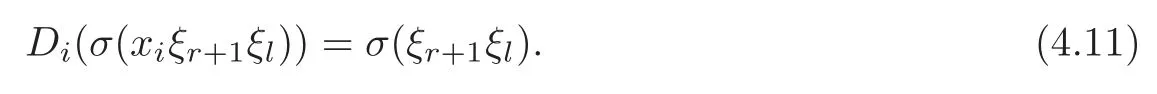

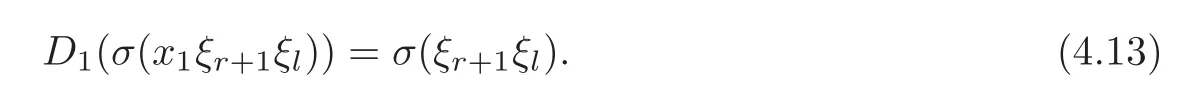
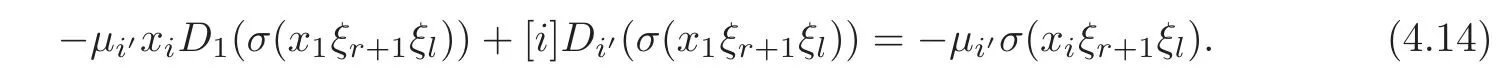
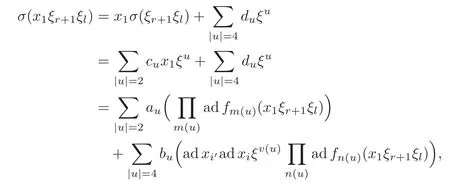
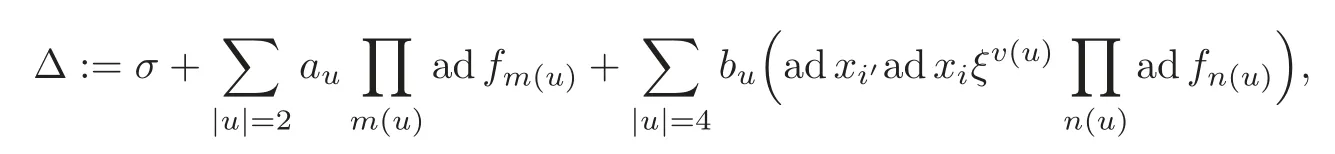
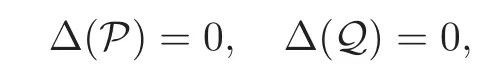
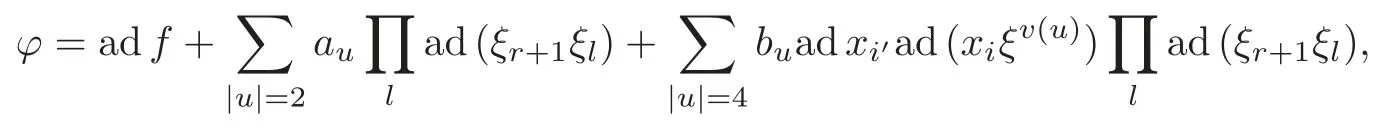
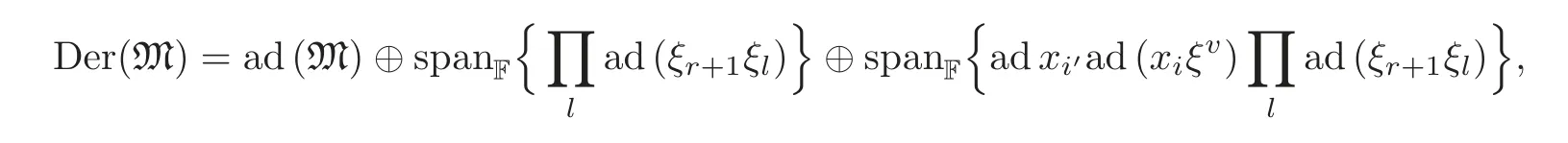
 Chinese Annals of Mathematics,Series B2015年2期
Chinese Annals of Mathematics,Series B2015年2期
- Chinese Annals of Mathematics,Series B的其它文章
- A Spectral Method for the Electrohydrodynamic Flow in a Circular Cylindrical Conduit
- Hypercube and Tetrahedron Algebra?
- Perturbed Riemann Problem for a Scalar Chapman-Jouguet Combustion Model?
- The Uniqueness of Inverse Problem for the Dirac Operators with Partial Information?
- Moments of L-Functions Attached to the Twist of Modular Form by Dirichlet Characters?
- Sharp Inequalities for BMO Functions?
