Perturbed Riemann Problem for a Scalar Chapman-Jouguet Combustion Model?
Meina SUN
1 Introduction
The Chapman-Jouguet(CJ for short)combustion theory describing the combustible gas with an infinite reaction rate plays an important role in gas dynamics(see[2,5,22]).Because of the difficulty of combustion problems in gas dynamics,there are few results for the CJ gas dynamic combustion except for the Riemann problems in[4](a solution involving only detonation),[21](a solution involving only def l agration),and[25](a solution satisfying the so-called geometrical entropy conditions).
In[13],from the one-dimensional combustion equation written in Lagrangian coordinates for the simple reactant to the product mechanism,Majda proposed the simplified scalar combustion model as
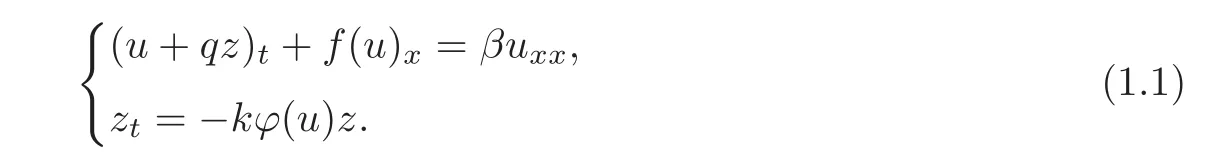
It is hoped that this qualitative model retains most of the essential features of the Lagrangian equations,except the species dif f usion(see[14]).Hereuis a lumped gas-dynamical variable combining aspects of specific volume,particle velocity and temperature,zmeasures the mass fraction of unburnt gas,and the fluxf(u)is required to satisfy

The viscosity coefficientβ,the chemical binding energyqand the reaction ratekare all positive constants.The ignition function?(u)is the Heaviside function as follows:
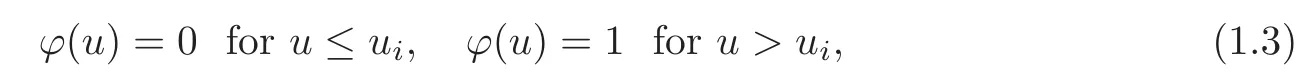
whereuiis the ignition temperature.This model was extensively studied as it is perhaps the most amenable one of all the models to rigorous mathematical analysis.Ying and Teng[23]studied the Riemann solution of(1.1)atβ=0 where the fluxf(u)was relaxed to satisfyf??(u)>0.They obtained the limit of the solution asktends to infinity and defined the limit function as the solution of the Riemann problem for the corresponding CJ model
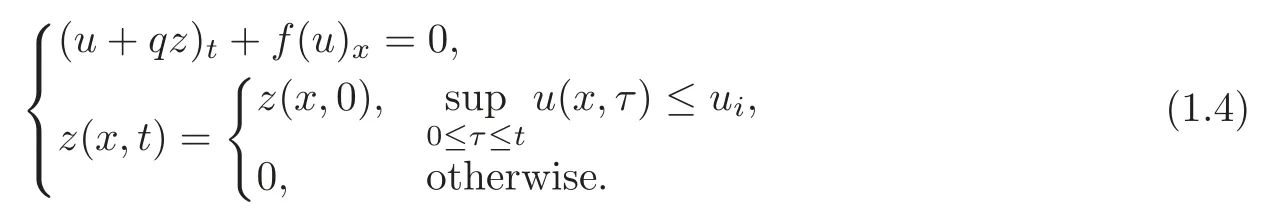
Based on Ying and Teng’s results,Liu and Zhang[9]summarized a set of entropy conditions,including pointwise and global entropy conditions,with which they obtained the uniqueness of the Riemann solution of the CJ model(1.4).The CJ model(1.4)with convex or nonconvex fl uxesf(u)was also considered in[1,6–7,16–17,19–20,24].
Although there is some good qualitative agreement between the behaviors of solutions of the model system(1.1)and the observed phenomena such as the appearance of“detonation spikes”in Majda model solutions,unfortunately de fl agration waves do not occur in the Majda model and this is one limit of its utility.In[10],Lyng and Zumbrun developed a stability index for weak and strong detonation waves in the context of the Majda model with a modi fied,bump-type ignition function
instead of the step-type function in[13],whereuianduidenote lower and upper ignition thresholds respectively.Hereucan be interpreted more precisely as a particle velocity,and then?takes the form?=ψ(T(u)),whereT(u)denotes temperature,ψis a standard,steptype ignition function,ψ=0 below some ignition temperatureTiand positive above,andT(u)is quadratic and concave-down withT(ui)=T(ui)=Ti.This agrees qualitatively with the physical dependence of temperature on velocity along the one-dimensional flow of the traveling wave ODE for the Zeldovich-von Neumann-Dring(ZND for short)model(see[10–12]for more detailed physical background).Under the same requirement(1.2),the Majda model allows for the existence of weak def l agration prof i les when choosing this bump-type ignition function,while the step-type ignition function does not[10].
In this paper,we consider the CJ model for whichβis set zero,kis taken to be infinite and?(u)has a bump-type form as
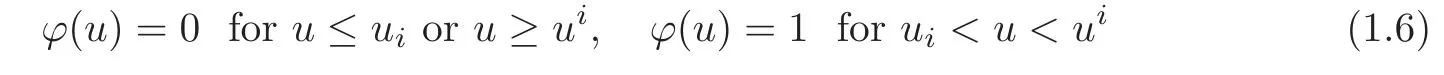
in(1.1).So it can be expressed as
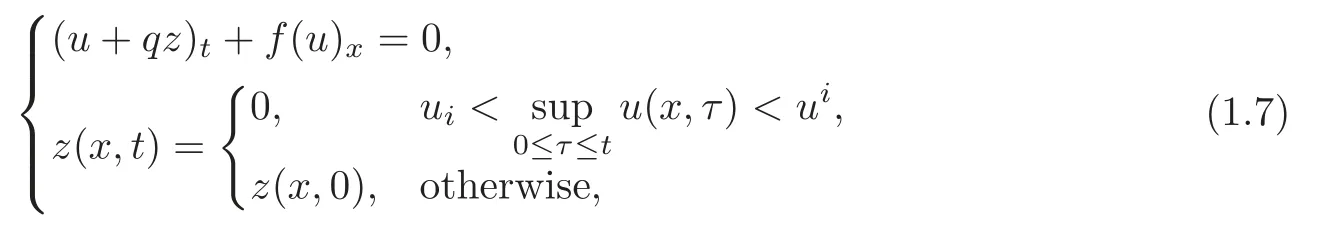
wheref(u)satisfies(1.2)throughout the present paper following[13].The Riemann problem for(1.7)was studied in[18].
For reactive gas,it is very interesting to study the nonlinear stability and instability of flows with combustion waves.In this paper,our purpose is to investigate whether the combustion waves in the Riemann solutions are stable or not due to the perturbation of the initial data.Therefore we deal with the perturbed Riemann problem(1.7)and the following initial data:
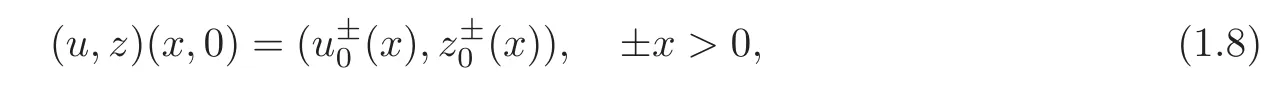
whereare arbitrary smooth functions withandequal a constant 1 for unburnt gas and 0 for burnt gas.The initial data(1.8)is a perturbation of the corresponding Riemann data
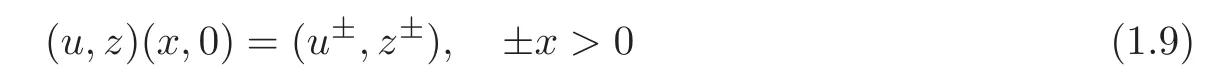
in the neighborhood of the origin.There is another motivation to study the perturbed Riemann problem(1.7)–(1.8).As is well-known that an error is unavoidable in numerical simulation and the error forms a perturbation of the initial data.So there may exist some numerical results which are unreadable and puzzle numerical analysts.For instance,the error may transform a strong detonation to a weak def l agration in the numerical solutions in[1,26],while the theoretical results in[16]give a reasonable explanation for this phenomenon.Thus the results of the present paper provide a preparation of theoretical analysis for the numerical simulation for the Majda model with a bump-type ignition function.
Under the entropy conditions proposed in[18],we obtain the unique perturbed Riemann solution of(1.7)–(1.8)by using the method of characteristic analysis(also called planar phase portrait analysis).We find that for most cases,the combustion waves in the corresponding Riemann solutions retain their forms after perturbation,while for some other cases,the perturbation brings essential changes to the combustion waves.That is,the perturbation may transfer a Chapman-Jouguet detonation into a strong detonation,a strong detonation into a weak def l agration following a shock wave under some conditions which does not happen for(1.4)with convex flux.The interesting phenomenon that burning happens although the corresponding Riemann solution does not contain combustion waves can also be observed,which exhibits the instability for the unburnt state.The perturbed Riemann problem for(1.4)was investigated in[16,20],and the perturbation on initial binding energy for(1.7)was considered in[15].
This paper is organized as follows.In Section 2,we present some preliminaries including the pointwise and global entropy conditions,and the Riemann solutions of(1.7)and(1.9).In Section 3,the construction of the perturbed Riemann solution of(1.7)–(1.8)is exhibited.Finally,the conclusion and discussion are drawn in Section 4.
2 Preliminaries
In this section,we sketch some results on the Riemann solutions of(1.7)and(1.9)for completeness,and the detailed study can be found in[18].
We seek self-similar solutions(u(ξ),z(ξ))of the Riemann problem for(1.7)and(1.9)whereIt is easy to show thatz(ξ)is piecewise constant,0 or 1,and the smooth solutionsu(ξ)are constant states or rarefaction waves(abbr.R):u(ξ)=(ξ).
A jump of the solution(u,z)=(u,z)(x,t)atx=x(t)should satisfy the Rankine-Hugoniot condition

whereetc.,and the assumption(1.2)determines thats≥0 if[z]=0.
Besides(2.1),we need some criteria to determine which kinds of discontinuities are admissible.Then the following pointwise entropy conditions are suggested in[10,18].
(1)Pointwise entropy conditions.
(A)For noncombustion discontinuities across which particles do not burn,the following two kinds are admissible:
(a)it is a shock(abbr.S)supplemented by the Lax characteristic conditionf?(ul)>s>(ur);
(b)[z]0,[u]=0?s=0,it is a contact discontinuity(abbr.J);
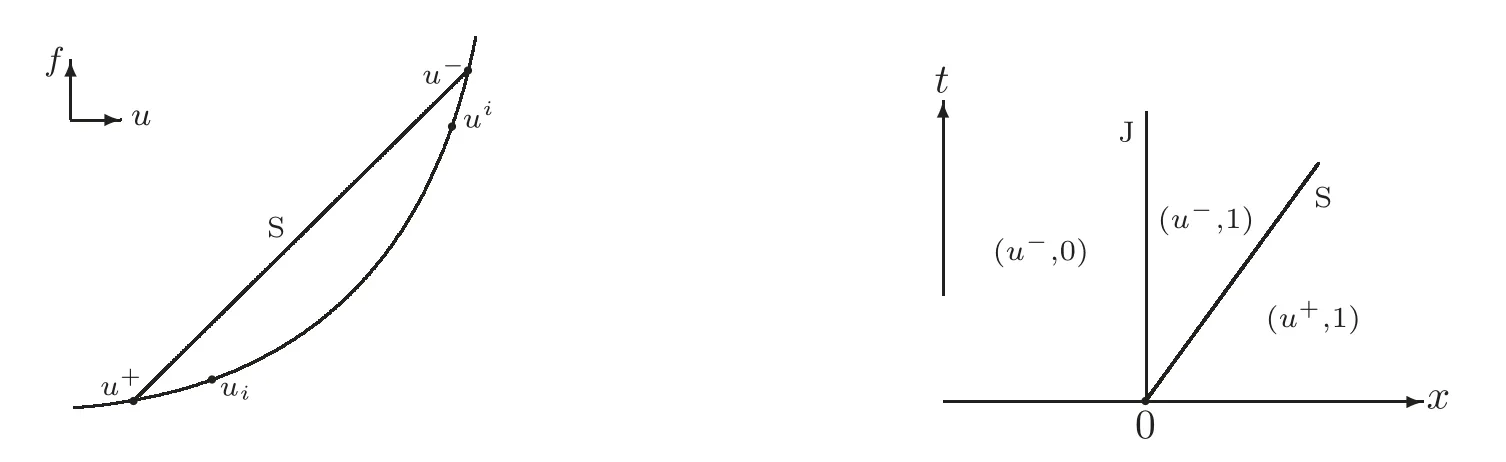
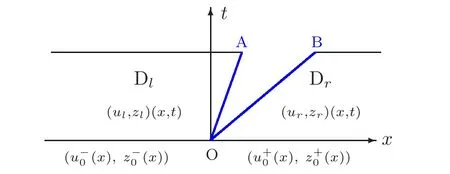
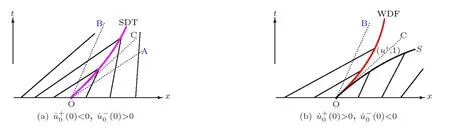
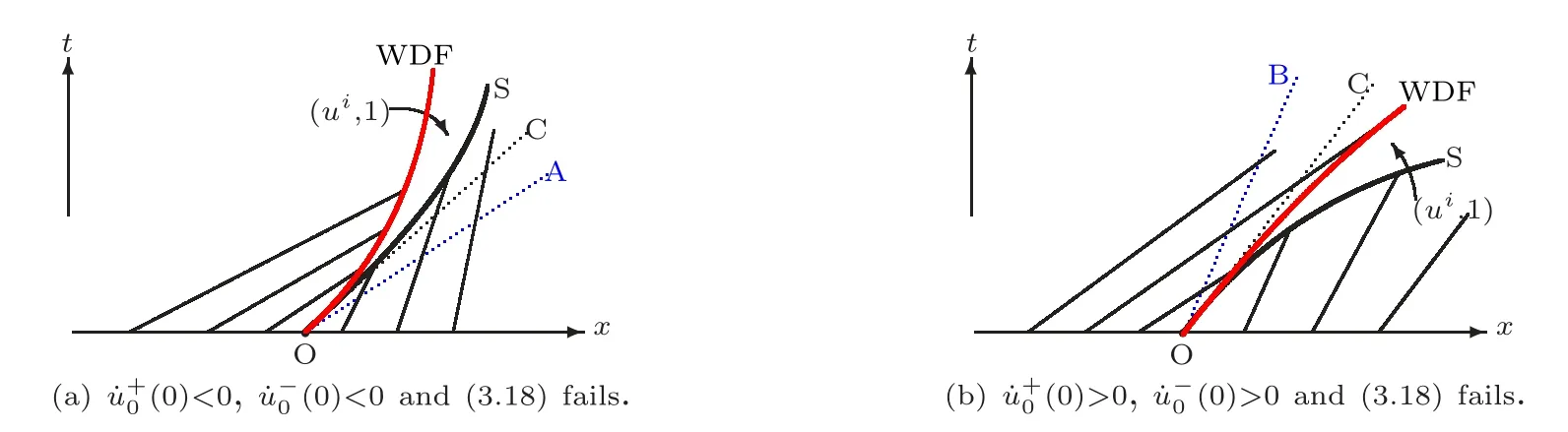
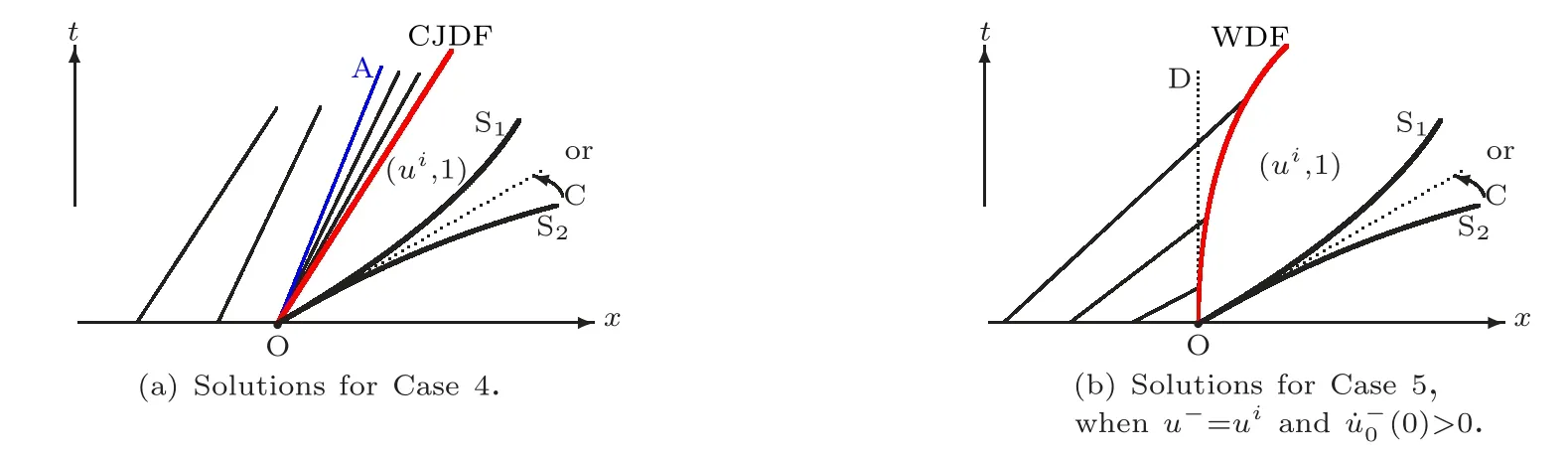
(B)For combustion jumps across which particles burn:[z]0,[u]0,the following four kinds are admissible.Two states(ul,zl)and(ur,zr)connected by a combustion wave withs>0 must satisfyzl=0,ui (a)Iful>ur,it is compressive,called (i)a strong detonation(abbr.SDT)for(ul)>s>(ur); (ii)a Chapman-Jouguet detonation(abbr.CJDT)for(ul)=s>(ur). (b)Iful (i)a weak def l agration(abbr.WDF)fors<(ul),(ur)andur=ui; (ii)a Chapman-Jouguet def l agration(abbr.CJDF)for(ul)=s<(ur)andur= We call R,S,J,SDT,CJDT,WDF and CJDF elementary waves for(1.7). In[18],we find that the aforementioned entropy conditions cannot guarantee the uniqueness of Riemann solutions of(1.7)and(1.9).Therefore the global entropy condition analogous to[7,9,25]is needed. (2)Global entropy condition. If the Riemann problem for(1.7)and(1.9)has several solutions satisfying the pointwise entropy conditions,we choose the one for which the propagation speed of the combustion wave is as slow as possible. In all,a combustion solution(u,z)is admissible,if it satisfies both the pointwise entropy conditions and the global entropy condition.The Riemann problem of(1.7)and(1.9)subject to the above entropy conditions can be solved uniquely. Now we briefly review the Riemann solutions of(1.7)and(1.9)for the most interesting situationz+=1,z?=0,u+≤ui For the caseu+≤ui Whenu+≤ui (i)R(u?,0;u1,0)+CJDT(u1,0;u+,1),ifui (ii)SDT(u?,0;u+,1),ifu1 (iii)WDF(u?,0;ui,1)+S(ui,1;u+,1),ifu2 where the notationsq?>0,u?∈(u+,ui),u1andu2satisfy respectively,andu+ Whenu+≤ui (i)R(u?,00)+CJDF(0;ui,1)+S(ui,1;u+,1),ifui (ii)WDF(u?,0;ui,1)+S(ui,1;u+,1),if For the caseu+≤ui,u?≥ui,the unique admissible solution of(1.7)and(1.9)is the noncombustion solution which can be denoted byJ(u?,0;u?,1)+S(u?,1;u+,1)(see Figure 1). Figure 1 Solution for u+≤ui,u?≥ui. We will investigate the solutions for the discontinuous initial value problem(1.7)–(1.8)in a neighborhood of the origin(t>0)in the(x,t)plane.In fact,for the smooth solution(z=constant),(1.7)reduces to the scalar conservation law for which the perturbed Riemann problem was studied in[3].Hence by[8],the classical solution(ul,zl)(x,t)(resp.(ur,zr)(x,t))can be defined in a strip domain Dl(resp.Dr)locally in time.The strip domain Dlhas the characteristic OA:x=λ(u?)tas the right boundary,and Drhas the characteristic OB:x=λ(u+)tas the left boundary,whereλ(u):=.For example,see Figure 2 for the case 0<λ(u?)<λ(u+). Figure 2 The strip domain Dl,rfor 0<λ(u?)<λ(u+). By the one-side nature of model(1.7),we find that only three situations as follows are interesting(see[18]): In the following,we focus our attention just on the typical case(i),for the reason that the discussions for the other two cases can be reduced to that of this typical one.In fact,for cases(ii)and(iii),a combustion wave CJDF or WDF appears in the corresponding Riemann solution(see[18]),so the discussions for these two cases are the same as those of the following Cases 3–4. We will construct the perturbed Riemann solution of(1.7)–(1.8)case by case according to the different solutions of the corresponding Riemann problem(1.7)and(1.9). Case 1A combustion wave CJDT appears in the corresponding Riemann solution. The occurrence of this case depends on the conditionu+≤ui It can be proved that the perturbation of the initial data has influence on the CJDT which turns to be an SDT forwhereas the CJDT remains for(0)>0.Hereafter,the dot(·)means derivative. Lemma 3.1The perturbed solution of(1.7)–(1.8)is anSDTif and only if ProofSuppose that there is a combustion jumpx=x(t)with(0)=λ(u1)and(0)≤0 in the domainλ(u?)t andul(x,t)is a centered rarefaction wave defined by We now prove thatIn fact,(0)can be calculated as follows.We may write the first equation in(3.2)in the form Then differentiating(3.4)with respect tot,one obtains Note that alongx=x(t), which means Thus if we consider(3.5)att=0,we find where we have As forby differentiating(3.3)with respect totalongx=x(t)and settingt=0,we get which implies Substituting(3.7)and(3.9)into(3.6)yields which shows that(0)has the same sign asby noticing thatu++q Conversely,ifit is possible by the analysis above to construct a combustion jumpx=x(t),which is a solution of(3.2)and lies in the domainλ(u?)t We turn our attention now to the perturbed solution of(1.7)–(1.8)for Lemma 3.2The perturbed solution of(1.7)–(1.8)is aCJDTif and only if ProofIfby the entropy conditions,such a CJDT:x=x(t)with˙x(0)=λ(u1)as should be constructed near the origin.Similarly the sign of(0)can be determined as follows.We consider the equation differentiate with respect totalongx=x(t),and sett=0.This gives(3.10),where we have used the fact that alongx=x(t), namely, Thus,from(3.10),we see that¨x(0)>0.A solution of(1.7)–(1.8)can then be defined as(ur(x,t),1)on the right-hand side ofx=x(t)and(ul(x,t),0)on the left-hand side ofx=λ(u?)t.The state on the left-hand side ofx=x(t)betweenx=λ(u?)tandx=x(t)is(u(x,t),0).The characteristic of the solution in the domainλ(u1)t≤x Figure 3 The perturbed solutions for Case 1,where OC:x=λ(u1)t. In the same way as in Lemma 3.1,it can be proved that the conditionis necessary for a solution constructed as above. Case 2A combustion wave SDT appears in the corresponding Riemann solution. This case happens if and only ifu+≤ui,u1 It is obvious that the SDT retains its form whenu1 Now we consider the complicated caseu?=u2.Motivated by the Riemann solution,it is possible to define a combustion jumpx=x(t)by solving the problem(3.2).Whether anx=x(t)so defined is an SDT depends on whether the stability conditionholds for it. Let us do some analysis first.For anyur(x,t),we may define?u(ur)>u?,such that Thenx=x(t)is an SDT if and only if along the curvex=x(t),it holds that Differentiating the first equation in(3.12),we can get which,by lettingur=u+,becomes Using the condition(0)=w(u+,ui),we have so that In view of(3.15)and(3.17),we see that(3.13)can be written as (i)Whenand(3.18)obviously holds.Moreover,we can derive(0)<0 for the SDT by noticing thatu++q (see Figure 4(a)). Figure 4 The perturbed solutions for Case 2,where OC:x=w(ui,u+)t. (ii)Whenand(3.18)certainly fails.Therefore,we should not expect the combustion jump to be SDT.By the entropy conditions,a WDF:x=x1(t)should be constructed in the domainλ(u+)t Then we construct a shock wave S:x=x2(t)in front of the WDF to connectuiandur(x,t),i.e., which lies in the domainw(ui,u+)t≤x2(t)<+∞.We now determine the sign of(0)and(0).With a similar calculation,it can be obtained from(3.20)–(3.21)that where the condition(0)=(0)=w(ui,u+)is used.Sinceui+q>u2andui>u+,we see from(3.22)thatandThe solution is illustrated in Figure 4(b). (iii)It remains to discuss the cases:andand0.Since the discussions for these two cases are similar,we here just give the discussion forandin detail. If(3.18)is satisfied,the perturbed solution contains an SDT:x=x(t)satisfying(3.2),and it can be claimed that(0)<0.In fact,note that 0 Combining(3.18)and(3.23),we have so that(3.19)holds.Thus the statement(0)<0 follows. If(3.18)is invalid,a WDF:x=x1(t)following a shock wave S:x=x2(t)appears near the origin by the entropy conditions,where the WDF and S are given by(3.20)–(3.21),respectively.In order to show the existence of the shockx=x2(t),we need the priori estimate:(0)<(0)<0.To prove this,we should notice(3.22)and the contrary of(3.18)which give that(0)<0,(0)<0 and Hence there exists a solutionx=x2(t)of(3.21)by virtue ofx1(0)=x2(0)=0,(0)=(0)=w(ui,u+),(0)<(0)<0(see Figure 5(a)).We remark that in the case ofand0<(0)<(0)can be obtained in the same way(see Figure 5(b)). Figure 5 The perturbed solutions for Case 2,where OC:x=w(ui,u+)t. Thus we have finished the discussion for Case 2.In brief,the solution of(1.7)–(1.8)may contain an SDT if(3.18)holds;otherwise a WDF following a shock may appear. Case 3A combustion wave WDF appears in the corresponding Riemann solution. In this case,the initial data have two possibilities:u+≤ui,u2 It is easy to find that the perturbed solution for this case is governed by the corresponding Riemann solution at the origin.That is,a WDF:x=x1(t)withsatisfying(3.20)should be constructed near the origin due to the entropy conditions,ahead of which is a shockx=x2(t)with(0)=w(ui,u+)satisfying(3.21). Case 4 Acombustion wave CJDF appears in the corresponding Riemann solution. The appearance of this case depends on the conditionu+≤ui,ui We can see that,for this case,the perturbation has no influence on the combustion wave CJDF:which propagates with the speedλ(?u)in the neighborhood of the origin.Furthermore,it can be derived similarly as before that(resp.corresponds to the shock S1(resp.S2),which connectsuiandur(x,t)(see Figure 6(a)). Case 5The corresponding Riemann solution is J+S. This case occurs whenu+≤ui,u?≥uiare satisfied(see Figure 2.1). It is obvious that the structure for the perturbed solution is still J+S ifu?>ui.For the boundary caseu?=ui,there exist two possibilities as follows. (i)Whenwhich indicates thatul(x,t)>uiast>0,burning does not happen,and the solution J+S can be constructed in the neighborhood of the origin. (ii)Whenthe perturbation gives birth to a combustion wave WDF by the entropy conditions.This phenomenon may owe to the instability of the unburnt state.The combustion wave WDF:x=x1(t)with(0)=0 satisfies(3.20),from which it can be derived that(see Figure 6(b)). Figure 6 The perturbed solutions for Cases 4–5,where OC:x=w(ui,u+)t,OD:x=0,S1corresponds to(0)<0,S2corresponds to(0)>0. So far we have finished constructing the solution of(1.7)–(1.8)completely.Our result can be summarized as follows. Under the pointwise and global entropy conditions,there exists the unique solution of the perturbed Riemann problem(1.7)–(1.8)near the origin.We can see that the combustion waves WDF and CJDF are stable since they can retain their forms after perturbation.The combustion wave CJDT is unstable ifunder which the perturbation transforms it into an SDT,whereas the CJDT is stable ifAs for an SDT,it is unstable just for the boundary case:u?=u2and(3.18)fails,under which the perturbation transforms an SDT into a WDF following a shock wave.Especially,we can observe the interesting phenomenon that burning happens although the corresponding Riemann solution does not contain combustion waves,which exhibits the instability of the unburnt state. AcknowledgementsThe author is grateful to Professor Wancheng Sheng and Tong Zhang for their ardent help.She is also grateful to the referees for their careful reading of the original manuscript and helpful comments. [1]Bao,W.and Jin,S.,The random projection method for hyperbolic conservation laws with stif freaction terms,J.Comput.Phys.,163,2000,216–248. [2]Bdzil,J.B.and Stewart,D.S.,The dynamics of detonation in explosive systems,Annual Review of Fluid Mechanics,39,2007,263–292. [3]Chang,T.and Hsiao,L.,The Riemann Problem and Interaction of Waves in Gas Dynamics,Pitman Monoger,Surveys Pure Appl.Math.,Vol.41,Longman,Essex,1989. [4]Chorin,A.J.,Random choice methods with application to reacting gas flow,J.Comput.Phys.,25,1977,253–272. [5]Courant,R.and Friedrichs,K.O.,Supersonic Flow and Shock Waves,Interscience,New York,1948. [6]Fickett,W.,Detonation in miniature,Amer.J.Phys.,47,1979,1050–1059. [7]Li,J.and Zhang,P.,The transition from Zeldovich-von Neumann-D¨oring to Chapman-Jouget theories for a nonconvex scalar combustion model,SIAM J.Math.Anal.,34,2003,675–699. [8]Li,T.T.,Global Classical Solutions for Quasilinear Hyperbolic Systems,John Wiley and Sons,New York,1994. [9]Liu,T.P.and Zhang,T.,A scalar combustion model,Arch.Rational Mech.Anal.,114,1991,297–312. [10]Lyng,G.and Zumbrun,K.,A stability index for detonation waves in Majda’s model for reacting flow,Physica D,194,2004,1–29. [11]Lyng,G.and Zumbrun,K.,One-dimensional stability of viscous strong detonation waves,Arch.Rational Mech.Anal.,173,2004,213–277. [12]Lyng,G.,Raoof i,M.,Texier,B.and Zumbrun,K.,Pointwise Green function bounds and stability of combustion waves,J.Differential Equations,233,2007,654–698. [13]Majda,A.,A qualitative model for dynamic combustion,SIAM J.Appl.Math.,41,1981,70–93. [14]Rosales,R.R.and Majda,A.,Weakly nonlinear detonation waves,SIAM J.Appl.Math.,43,1983,1086–1118. [15]Shen,C.and Sun,M.N.,The perturbation on initial binding energy for a Majda-CJ combustion model,Applicable Analysis,92,2013,2115–2126. [16]Sheng,W.C.,Sun,M.N.and Zhang,T.,The generalized Riemann problem for a scalar nonconvex Chapman-Jouguet combustion model,SIAM J.Appl.Math.,68,2007,544–561. [17]Sheng,W.C.and Zhang,T.,Structural stability of solutions to the Riemann problem for a scalar nonconvex combustion model,Discrete Contin.Dyn.Syst.,25,2009,651–667. [18]Sun,M.N.,Entropy solutions of a Chapman-Jouguet combustion model,Mathematical Models and Methods in Applied Sciences,22(9),2012,1250018,35 pages. [19]Sun,M.N.and Sheng,W.C.,The ignition problem for a scalar nonconvex combustion model,J.Differential Equations,231,2006,673–692. [20]Sun,M.N.and Sheng,W.C.,The generalized Riemann problem for a scalar Chapman-Jouguet combustion model,Z.Angew.Math.Phys.,60,2009,271–283. [21]Teng,Z.H.,Chorin,A.J.and Liu,T.P.,Riemann problems for reacting gas with applications to transition,SIAM J.Appl.Math.,42,1982,964–981. [22]Williams,C.D.,The detonation of explosives,Sci.Amer.,256,1987,98–104. [23]Ying,L.A.and Teng,Z.H.,Riemann problem for a reaction and convection hyperbolic system,Approx.Theory Appl.,1,1984,95–122. [24]Zhang,P.and Zhang,T.,The Riemann problem for scalar CJ-combustion model without convexity,Discrete Contin.Dynam.Systems,1,1995,195–206. [25]Zhang,T.and Zheng,Y.X.,Riemann problem for gas dynamic combustion,J.Differential Equations,77,1989,203–230. [26]Zhang,X.T.and Ying,L.A.,Dependence of qualitative behavior of the numerical solutions on the ignition temperature for a combustion model,J.Comput.Math.,23,2005,337–350.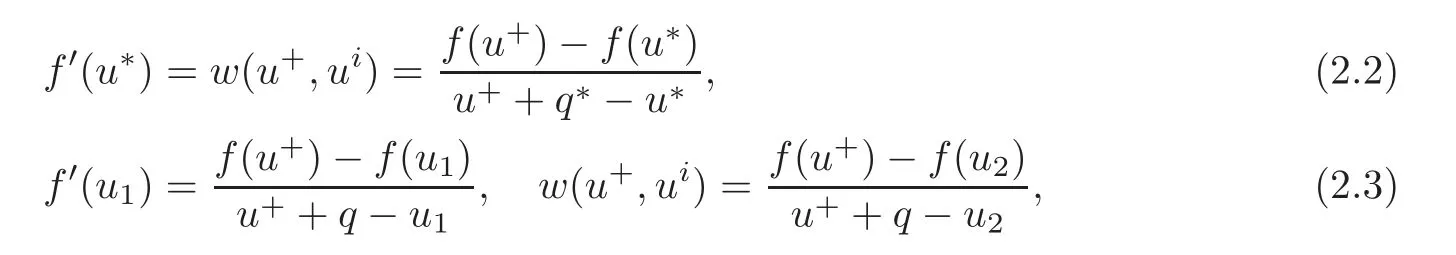
3 Solution of the Perturbed Riemann Problem

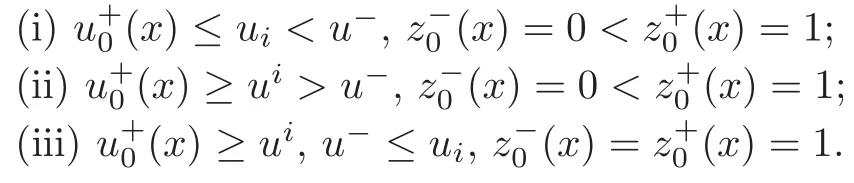
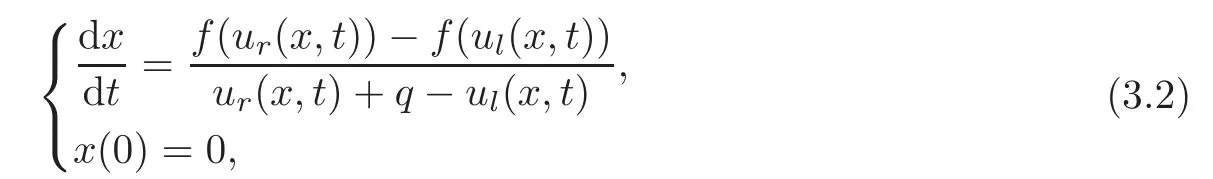
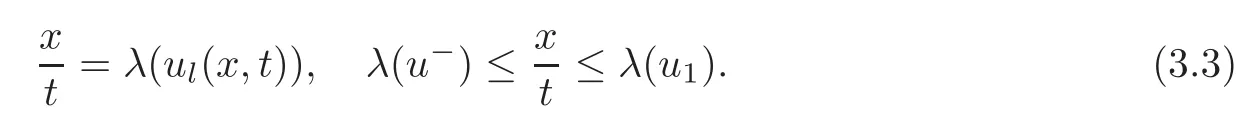
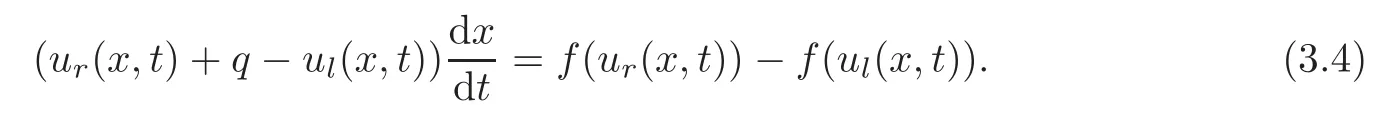
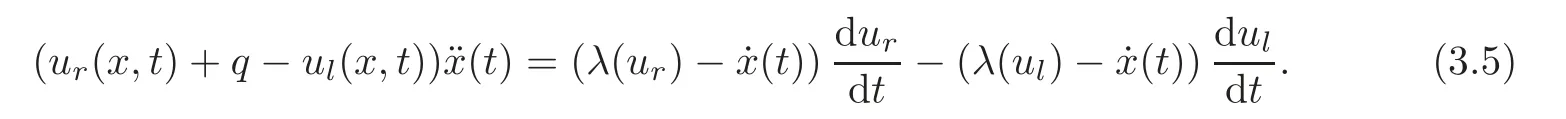
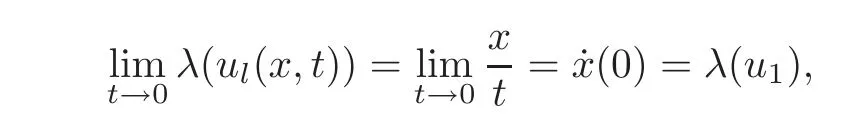
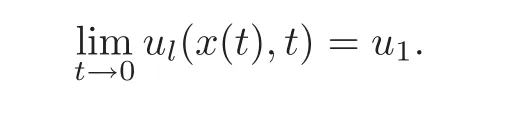
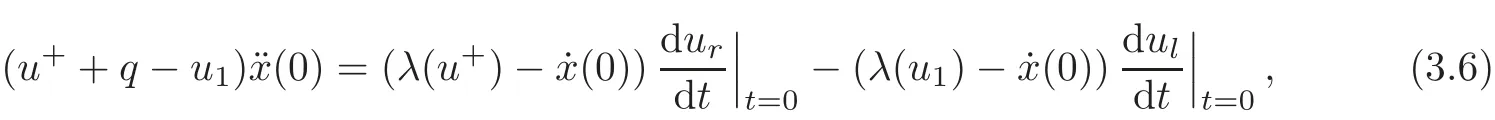
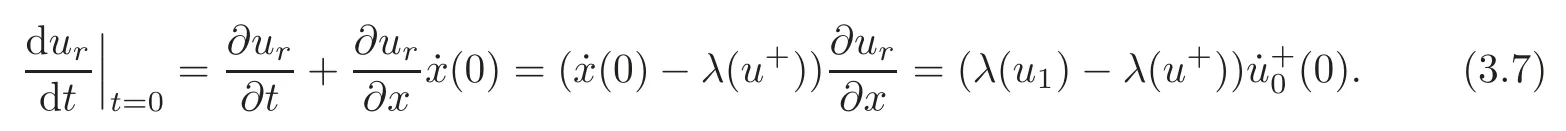
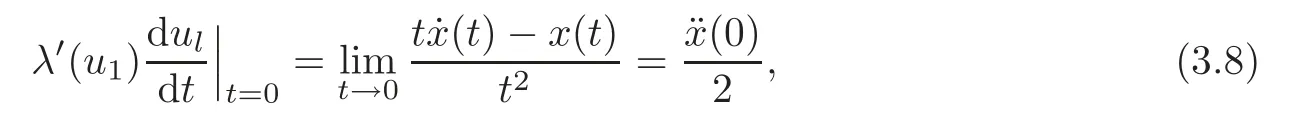

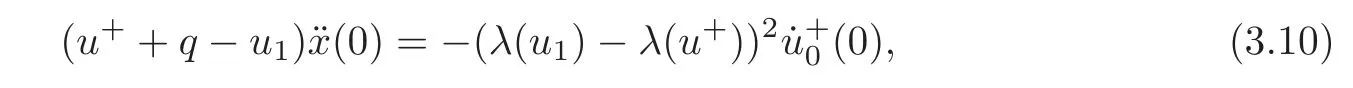
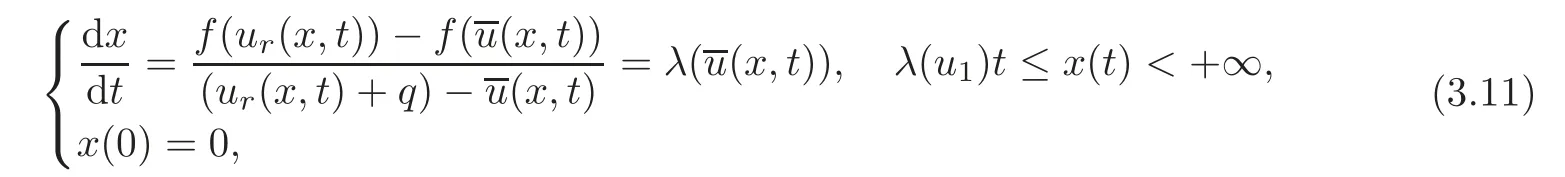
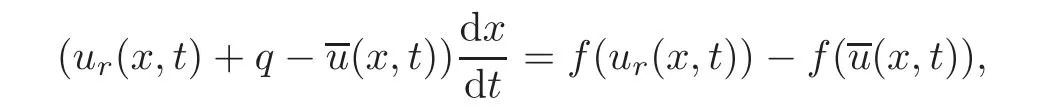
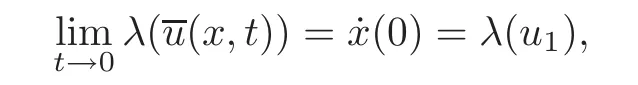
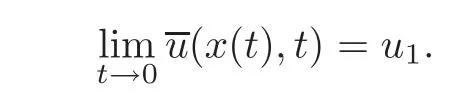

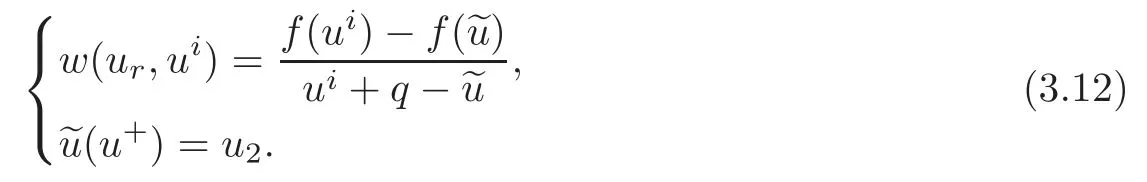

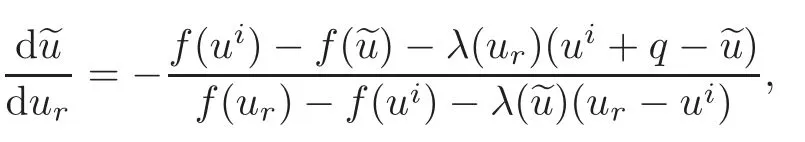
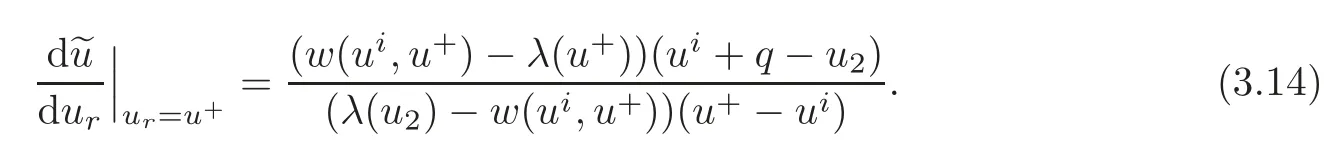
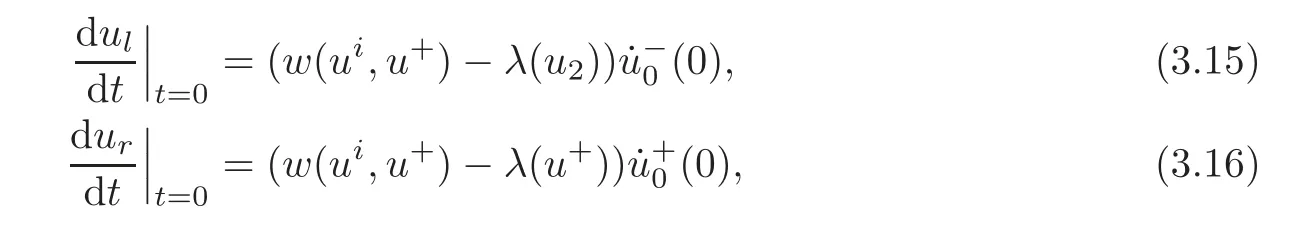
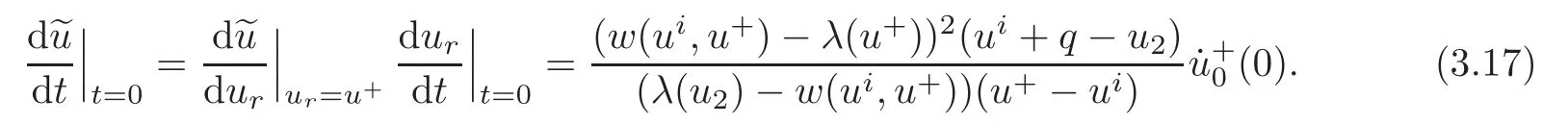
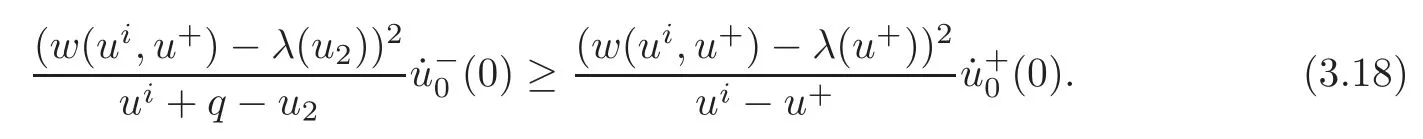
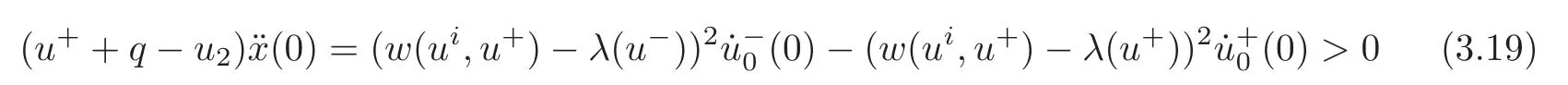
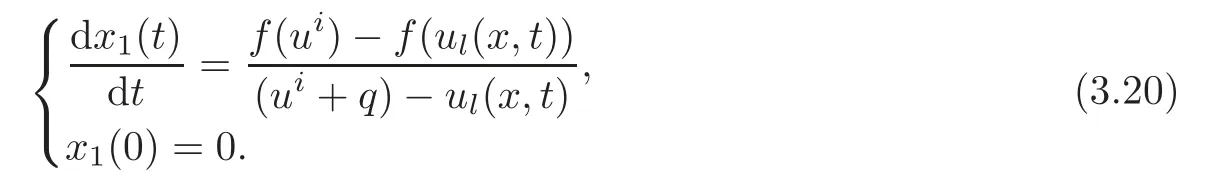

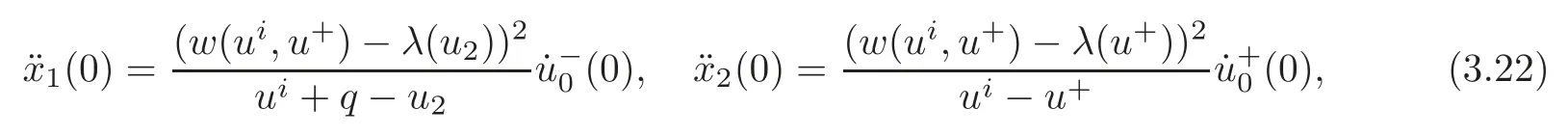
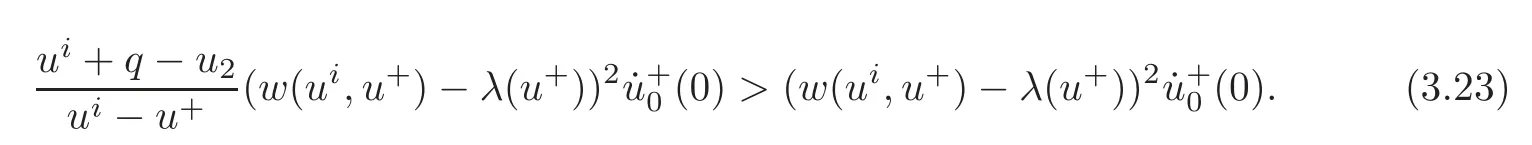
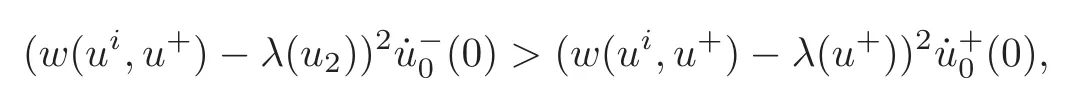
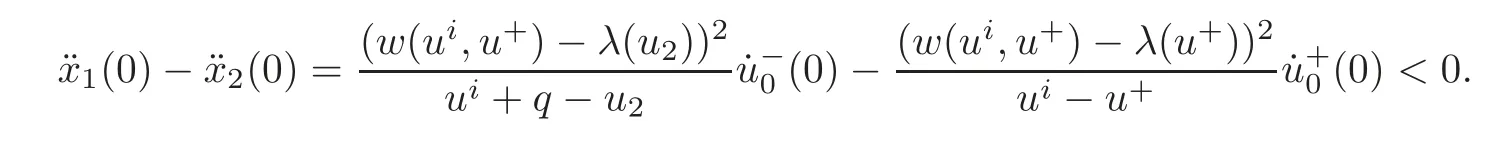
4 Conclusion
 Chinese Annals of Mathematics,Series B2015年2期
Chinese Annals of Mathematics,Series B2015年2期
