Sharp Inequalities for BMO Functions?
Adam OSE?KOWSKI
1 Introduction
A real-valued locally integrable function?defined on Rnis said to be in BMO,the space of functions of bounded mean oscillation,if

where the supremum is over all cubesQin Rnwith edges parallel to the coordinate axes,and
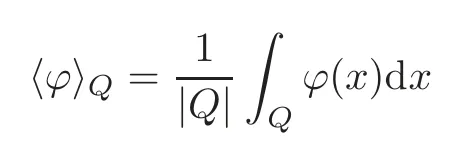
denotes the average of?overQ.We will consider a slightly less restrictive setting in which only the cubesQwithin a givenQ0are considered;to stress the dependence onQ0,we will use the notation BMO(Q0).
The BMO class,introduced by John and Nirenberg in[8],plays an important role in analysis and probability,since many classical operators(maximal,singular integral,etc.)mapL∞into BMO.Another remarkable result,due to Fefferman[4],asserts that BMO is a dual to the Hardy spaceH1.It is well-known that the functions of bounded mean oscillation have very strong integrability properties(see[8]).In particular,thep-oscillation
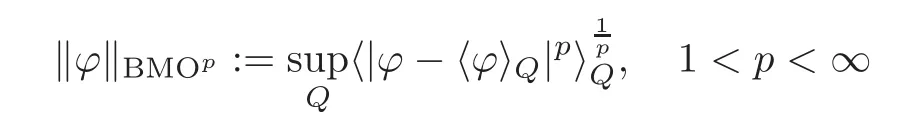
is finite for any?∈BMO.It turns out thatBMOpforms an equivalent norm on BMO(Rn).In what follows,we will work withBMO2and denote it simply byBMO.One of the reasons we choose this particular norm is that we have the identity
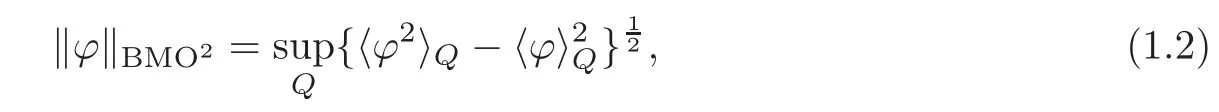
which makes the norm very convenient to handle;see below.Furthermore,from now on,we restrict ourselves to the casen=1.Then the cubes become intervals,and to stress that we work in the one-dimensional setting,we will replace the letterQwithI.
In the recent years,there has been a considerable interest in obtaining various sharp estimates for the BMO class.Probably the first result in this direction is that of Slavin[14]and Slavin and Vasyunin[15],which identifies the optimal constants in the so-called integral form of John-Nirenberg inequality.Namely,it was shown there that if?:IR satisfies?BMO(I)<1,then
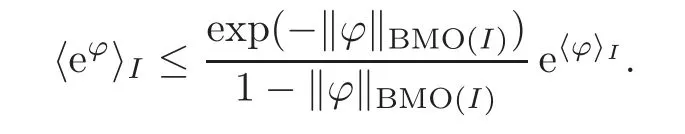
Furthermore,this bound is sharp in the sense that for eachε<1 there is a function?satisfying=εandIn particular,this shows that there exists no exponential estimate of the above type when
The following sharp version of the related classical weak form of John-Nirenberg inequality is due to Vasyunin[18]and Vasyunin and Volberg[20].Namely,ifε:=?BMO(I)<∞,then
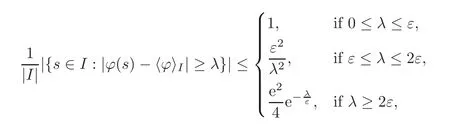
and for each value ofεandλ,the equality can be attained.Optimizing overλ,we get the sharp weak-type inequality

Here
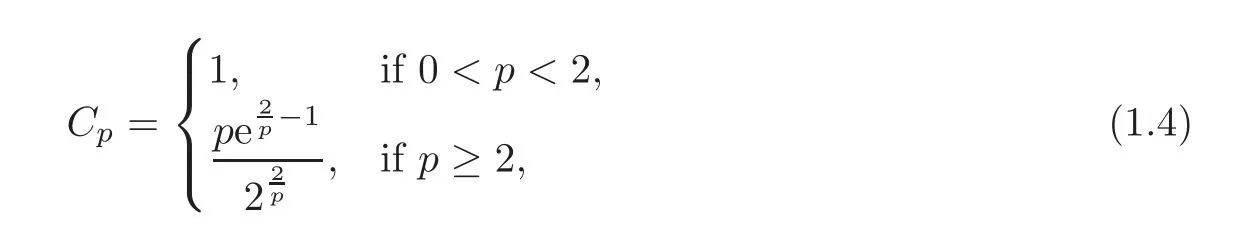
and
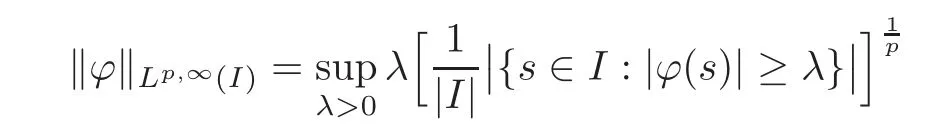
is the usual weakp-th quasinorm.We should also mention here a result of Korenovskii[9],who studied the weak-type constant for BMO space equipped with the normHe showed that the optimal(i.e.,the largest)value of the constantc2in the inequality
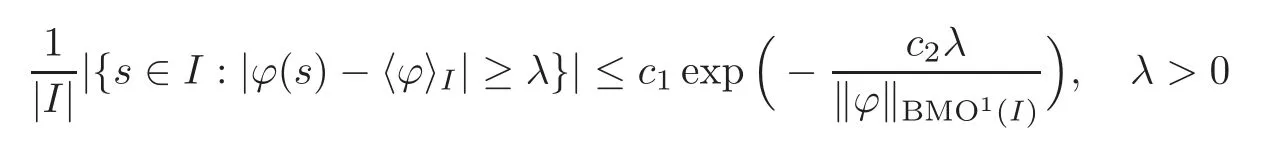
equalsThe reasoning rests on the careful analysis of the nonincreasing rearrangement of the function?.
There is a related work of Slavin and Vasyunin[16],which provides the sharp comparison of the normsandAmong other things,that paper contains the proof of the following statement:
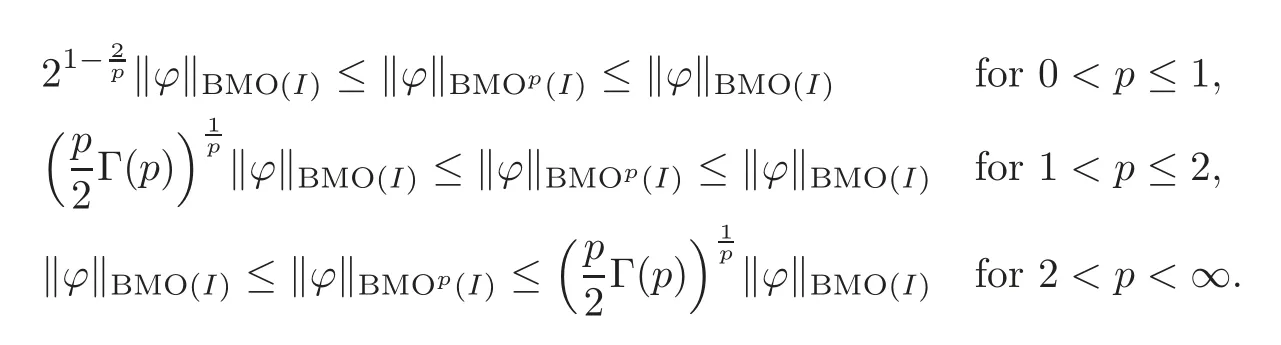
Furthermore,the right-hand side inequalities forp<2 and both left-and right-hand side inequalities forp>2 are sharp and attainable.
It should be pointed out here that except for Korenovskii’s result,all the estimates formulated above were established by use of a powerful technique,the so-called Bellman function method.Roughly speaking,the approach turns the problem of proving a given estimate for a BMO class into the search of a certain special function,enjoying appropriate majorization and concavity conditions.The method originates from certain extremal constructions in the dynamic programming(see the recent edition of the classical monograph of Bellman[1]).As observed by Burkholder[2–3]in the 1980s,the framework of optimal stochastic control can be modified appropriately and used in the study of sharp inequalities for martingale transforms.In the 1990s,in the works[11–12],Nazarov,Treil and Volberg noticed some deep connections between the Bellman approach and various aspects of harmonic analysis,and formulated the general modern framework of the technique.Since then,the method has been applied in numerous papers,in both harmonic analysis and probability.The literature on the subject is very large and it is impossible to review it here.We only refer the reader to the works[10,13,19],the papers mentioned above and the references therein.
Finally,we would like to mention here the recent work of Ivanishvili et al.[7],which treats the above BMO estimates from a much wider perspective.More specifically,it provides the detailed description of the machinery which can be used to prove a general estimate in the BMO setting(under some regularity conditions on the boundary value function).Consult also[6]for the short discussion on the subject.
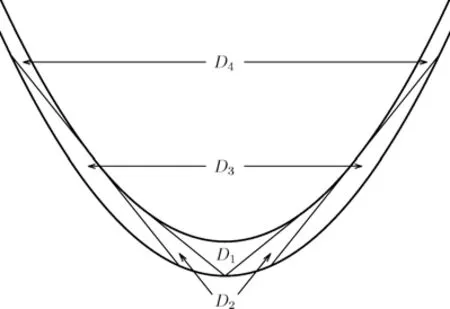
We turn our attention to the main results of this paper.As in[18,20],we will be interested in the weak-type estimates for BMO functions,but we will work under a different norming of the weak spaces.Namely,for 0 where the supremum is taken over all measurable subsetsEofIsatisfying|E|>0.It is wellknown(see[5])thatis an equivalent norm in the spaceLp,∞(for 1 Our main result can be stated as follows. Theorem 1.1Suppose that ? belongs to the classBMO(I).Then for any0 where Cpis given by(1.4).For each p the inequality is sharp. Thus,in comparison to(1.3),we see that the optimal constant under the new stronger norming ofLp,∞r(nóng)emains the same.As in the aforementioned papers,our approach will rest on the Bellman function method.We would like to point out here that the desired estimate does not fall into the scope of the(general)bounds covered by[6–7],since the corresponding boundary value function is not sufficiently regular.However,the arguments developed in these papers have turned out to be quite helpful during the search. We have organized this paper as follows.The next section is devoted to the proof of(1.5).The validity of this estimate is deduced from the existence of a certain special function.In Section 3,we exhibit some examples which show that for eachpequality can hold in(1.5);thus the constantCpappearing in this estimate can not be replaced by a smaller number. We start from the observation that it suffices to prove the inequality(1.5)forp≥2.Indeed,having successfully done this,we pick 0 Thus,in the remainder of this section,we assume thatp≥2.Suppose thatλ≥1 is a fixed parameter and consider the parabolic strip A key step in the analysis of the inequality(1.5)is to introduce the following Bellman function Bp,λ:Ω[0,∞): It is easy to see that Bp,λis well defined(i.e.,for each(x,y)∈Ω there exists at least one function?satisfying the required properties).Indeed,define whereI?andI+are the left and right half ofI,respectively.Then=x,=y,and to show the upper bound for the BMO norm of?,pick an arbitrary subintervalJofI.DenotingJ±=J∩I±,we compute that and hence1,asJis arbitrary. Actually,to show(1.5),we do not need the explicit formula for Bp,λ,but it suffices to have an accurate upper bound for this function.To provide such an estimate,let us first split Ω into the union of the following sets(see Figure 2 below): Figure 1 The regions D1–D4 Now,consider the functionBp,λ:Ω[0,∞)given by This function enjoys the following properties.First,observe that Second,note that we obviously have The final property ofBp,λis studied in a separate lemma below. Lemma 2.1The function Bp,λis locally concave,i.e.,it is concave along any line segment contained inΩ. ProofClearly,Bp,λis of classC∞on each(whereAodenotes the interior of a setA).Moreover,it is straightforward to check that the functionBp,λis continuous and of classC1in the interior of Ω:One needs to verify that the partial derivatives ofBp,λmatch appropriately at the common boundaries of the setsDi.We leave the necessary calculations to the reader.Thus,to establish the assertion,it suffices to show that the Hessian matrix ofBp,λis nonpositivedefinite in the interior of eachDi.SinceBp,λ(x,y)=Bp,λ(?x,y),it is enough to handle the matrixx,y)forx≥0 only.We start from observing that if(x,y)lies in the interior of one ofDi’s,then there exists a(short)line segment passing through this point,along whichBp,λis linear.This is clear when(x,y)(any line segment contained inD1does the job)or(x,y)∈(take a line segment of slope 2λ:Then the square rootis constant).When(x,y)∈we consider the line segment of slopeThen,fortsufficiently close to 0,we see that is a linear function oft.A similar calculation shows that for(x,y)∈the functionBp,λis linear along a(short)line segment of slopeThis“l(fā)ocal linearity”implies that the Hessian matrix ofBp,λhas determinant 0.Therefore we will be done if we prove that the second-order partial derivativeis nonpositive onBut this is simple:A little calculation shows thatequals and all the expressions are nonpositive. Now we will prove that Bp,λ≤Bp,λ.To accomplish this,we will require the following lemma,which can be found in[15](consult Lemma 4c there). Lemma 2.2Fix ε<1.Then for every interval I and every ?:IRwith≤ε,there exists a splitting I=I?∪I+such that the whole straight-line segment with the endpoints(±,±)is contained withinΩ.Moreover,the splitting parametercan be chosenuniformly(with respect to ? and I)separated from0and1. Now we will show the key majorization. Theorem 2.1For any p≥2and λ≥1,we haveBp,λ≤Bp,λ. ProofPick an arbitrary(x,y)∈Ω and let?:IR be an arbitrary function as in the definition of Bp,λ(x,y).Next,letε∈(0,1)be a fixed parameter and put=ε?;then,clearly,BMO(I)≤ε.Consider the following family{In}n≥0of partitions ofI,generated by the inductive use of Lemma 2.2.We start withI0={I};then,givenIn={In,1,In,2,···,In,2n},we split eachIn,kaccording to Lemma 2.2,applied to the function??,and put Next,we define functional sequencesandby the formulas whereIn(x)∈Inis an interval containingx(if there exist two such intervals,we pick the one which hasxas its right endpoint).An important observation,which is the consequence of the fact that we work with2-norm,is that for eachnthe pair(?n,ψn)takes values in Ω.Indeed,for anyJ∈Inwe have where the left bound is due to Schwarz inequality,and the right follows from(1.2)and the assumption=≤1. Now,we will show that for anyn≥0 and any 1≤k≤2n,we have To do this,note that?nandψnare constant onIn,k,while?n+1andψn+1are constant on the intervalsinto whichIn,ksplits.Therefore,dividing both sides by|In,k|,we see that the above estimate is equivalent to This bound follows from the local concavity ofBp,λand the fact that the whole line segment with endpoints is contained in Ω(which is guaranteed by Lemma 2.2).Summing(2.3)over allk=1,2,···,2n,we get Hence,by induction, for anyn=0,1,2,···.To handle the left-hand side,observe that To deal with the right-hand side of(2.4),letngo to infinity.Since the splitting ratio of Lemma 2.2 is bounded away from 0 and 1,we see that the diameter of the partitionIn(i.e.,tends to 0.Consequently,by Lebesgue’s differentiation theorem,we have?nandψnalmost everywhere onI.Combining the above facts with Fatou’s lemma,we see that(2.4)leads to so,by(2.1), It remains to letε1 and use continuity ofBp,λand Fatou’s lemma again.As the result,we obtain and since?was arbitrary,the bound Bp,λ(x,y)≤Bp,λ(x,y)follows. Remark 2.1Using examples similar to those which will appear in Section 3 below,one can show that we actually have an equality:Bp,λ=Bp,λ.However,this is quite elaborate and we will not need this;hence,we have decided not to include the details here. We turn to the inequality of Theorem 1.1. Proof of(1.5)By homogeneity,it is enough to show that if???BMO(I)≤1,then for anyE?Iof positive measure.Without loss of generality we may assume that?has integral 0 and thatIhas length one.PickEas above and decompose it into the union of Using the estimates Bp,λ≤Bp,λand(2.2),we get Furthermore,we obviously have Adding the two estimates above,we obtain an inequality which can be equivalently transformed into Now,suppose that|E|≤By a straightforward analysis of a derivative,we check that the right-hand side above,considered as a function ofλ∈[1,∞),attains its minimum forλ=1?ln(4|E|).Plugging this value into(2.6)and dividing throughout bywe obtain the inequality However,the functionattains its maximumThis shows(2.5)for small|E|.Next,suppose that the converse bound|E|>holds true.SinceSchwarz inequality yields On the other hand,we have This completes the proof of(2.5)and thus(1.5)is established. For each 0 We start with the easy case 0 Thus we must have the equality in(2.5)and the sharpness follows. Next,we turn to the more difficult casep>2.Consider the function?:[0,1]→R,given by the condition?(s)=??(1?s)and If we takethenand|?|≡ponE,so Therefore,all we need is the bound≤1.In other words,we must show that for each 0≤a Actually,by the symmetry of?,we may restrict ourselves toaWe split the reasoning into three separate parts. Step 1Let us start with the casea=0,b∈0,.Ifthen?is constant on[a,b]and=(p,p2)∈Ω.Ifthen the point(,)belongs to the line segmentSjoining(p,p2)and((p?2),(p?2)2).This is a consequence of and a similar identity with the same weights,which holds for the average of?2.Since the segmentSis contained within Ω(actually,it is tangent to the upper boundary of Ω),we see that(3.1)holds foras well.Next,suppose now thatIntegrating by parts,we obtain so(3.1)is satisfied.Finally,ifb∈,then arguing as in(3.2),we see that the point,)belongs to the line segment with the endpoints Again,this line segment is contained in Ω,so(3.1)is valid. Step 2Next,we turn our attention to the case 0 Therefore,we see that the points(),(,)and(,)are colinear.In addition,(,?2[0,a])and(?a,b],?2[a,b])lie at the opposite sides of the point(?[0,b],?2[0,b]).Furthermore,by Schwarz inequality,(?[a,b],?2a,b])lies on or above the lower boundary of Ω.Combining these observations with the analysis of the position of the point?[0,b],?2[0,b])carried out in Step 1 gives(3.1).Let us be a little bit more specific about this and take a look at the line segmentTjoining(?[0,a],?20,a])and.Ifthen it is tangent to the upper boundary of Ω,so(3.1)holds.Ifthen there exists a pointplying on the intersection of the upper boundary Ω and the interior ofT.This implies that the part ofT,which lies betweenpand(?0,b],?2[0,b]),lies above the upper boundary of Ω.Hence,by the convexity of the functions2+1,the whole line segment with endpoints(?[0,b],?2[0,b])and(?[a,b],?2[a,b])must be contained in Ω.Finally,ifb∈?,?,then the point(?[0,b],?2[0,b])belongs to the line segment joining(0,0)and(1,2)(tangent to the upper boundary of Ω),while(?[0,a],?20,a])lies on or above the line passing through(0,0)and(1,2).Therefore(?[a,b],?2[a,b])must lie on or below this line,and hence also lie on or below the upper boundary of Ω. Step 3Finally,we consider the casea< Furthermore,observe that Combining the two facts above,we conclude that≤1.By symmetry of?,we also have≤1.Since the point,lies on or below the line R×{1},which is tangent to the upper boundary of Ω.Thus,(3.1)follows. This completes the proof of the bound?BMO([0,1])≤1 and establishes Theorem 1.1. AcknowledgementThe author would like to thank the anonymous referee for the careful reading of the first version of this paper. [1]Bellman,R.,Dynamic programming,Princeton University Press,Princeton,2010. [2]Burkholder,D.L.,Boundary value problems and sharp inequalities for martingale transforms,Ann.Probab.,12,1984,647–702. [3]Burkholder,D.L.,Explorations in martingale theory and its applications,′Ecole d’Ete de Probabilit′es de Saint-Flour XIX—1989,1–66,Lecture Notes in Math.,1464,Springer-Verlag,Berlin,1991. [4]Fefferman,C.,Characterizations of bounded mean oscillation,Bull.Amer.Math.Soc.,77,1971,587–588. [5]Grafakos,L.,Classical and Modern Fourier Analysis,Pearson Education,Inc.New Jersey,2004. [6]Ivanishvili,P.,Osipov,N.,Stolyarov,D.,et al.,On Bellman function for extremal problems in BMO,C.R.Math.Acad.Sci.Paris,350,2012,561–564. [7]Ivanishvili,P.,Osipov,N.,Stolyarov,D.,et al.,Bellman functions for the extremal problems on BMO(in Russian),http://www.pdmi.ras.ru/preprint/2011/rus-2011.html. [8]John,F.and Nirenberg,L.,On functions of bounded mean oscillation,Comm.Pure and Appl.Math.,14,1961,415–426. [9]Korenovskii,A.,The connection between mean oscillations and exact exponents of summability of functions,Math.USSR-Sb.,71(2),1992,561–567. [10]Melas,A.D.,The Bellman functions of dyadic-like maximal operators and related inequalities,Adv.Math.,192,2005,310–340. [11]Nazarov,F.and Treil,S.,The hunt for Bellman function:Applications to estimates of singular integral operators and to other classical problems in harmonic analysis,Algebra i Analis,8,1997,32–162. [12]Nazarov,F.,Treil S.and Volberg,A.,The Bellman functions and two-weight inequalities for Haar multipliers,J.Amer.Math.Soc.,12,1999,909–928. [13]Os?ekowski,A.,Sharp martingale and semimartingale inequalities,Monografie Matematyczne,72,Birkh¨auser,Springer-Verlag,Basel AG,Basel,2012. [14]Slavin,L.,Bellman function and BMO,Ph.D.thesis,Michigan State University,2004. [15]Slavin,L.and Vasyunin,V.,Sharp results in the integral-form John-Nirenberg inequality,Trans.Amer.Math.Soc.,363,2011,4135–4169. [16]Slavin,L.and Vasyunin,V.,SharpLp-estimates on BMO,Indiana Univ.Math.J.,61,2012,1051–1110. [17]Slavin,L.and Volberg,A.,Bellman function and theH1?BMO duality,Harmonic analysis,partial differential equations,and related topics,113–126,Contemp.Math.,428,Amer.Math.Soc.,Providence,RI,2007. [18]Vasyunin,V.,The sharp constant in John-Nirenberg inequality,http://www.pdmi.ras.ru/preprint/2003/index.html. [19]Vasyunin,V.and Volberg,A.,Monge-Amp′ere equation and Bellman optimization of Carleson embedding theorems,linear and complex analysis,195–238,Amer.Math.Soc.Transl.Ser.2,226,Amer.Math.Soc.,Providence,RI,2009. [20]Vasyunin,V.and Volberg,A.,Sharp constants in the classical weak form of the John-Nirenberg inequality,Proc.Lond.Math.Soc.,108,2014,1417–1434.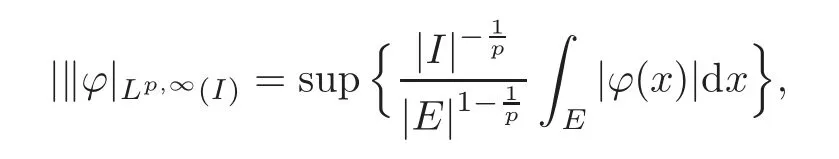
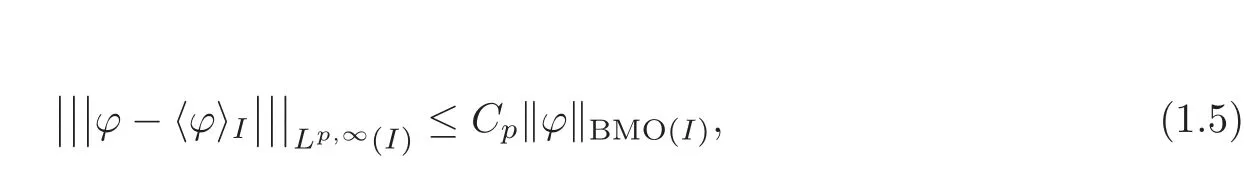
2 A Locally Concave Function and the Proof of(1.5)
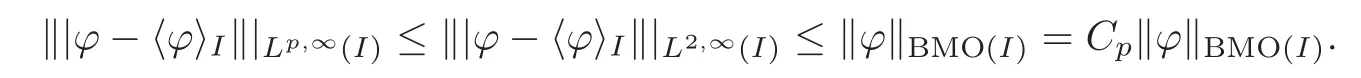
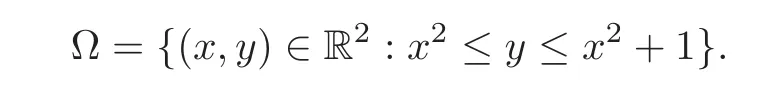
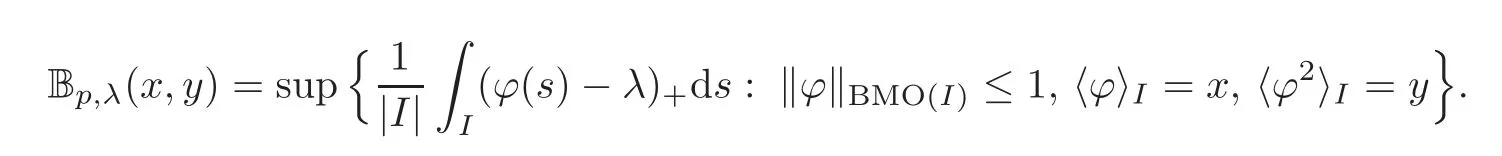
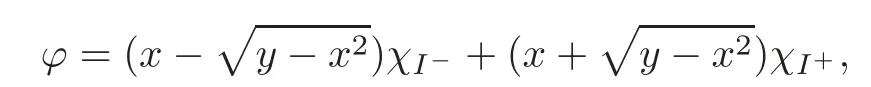
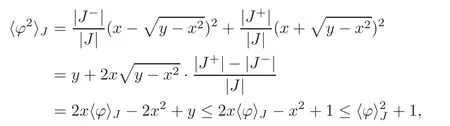
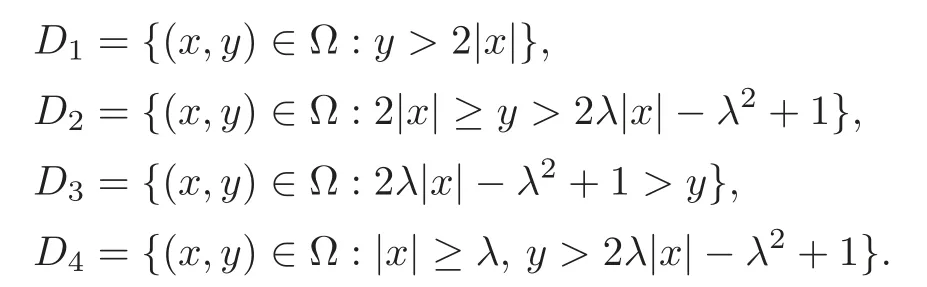
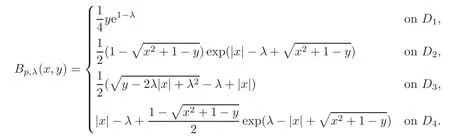
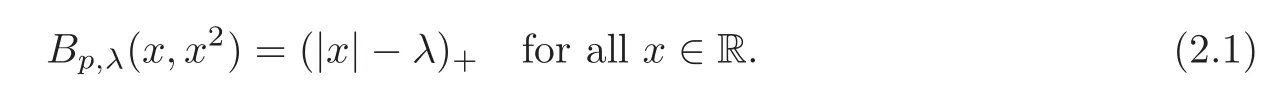
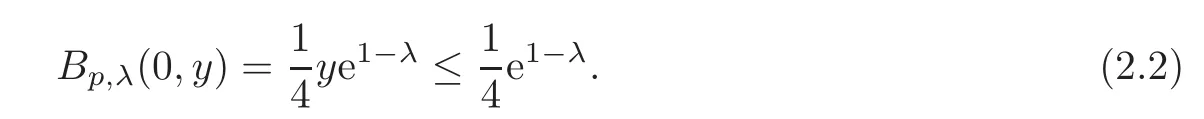
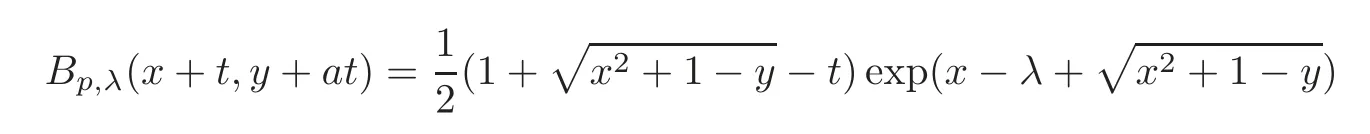
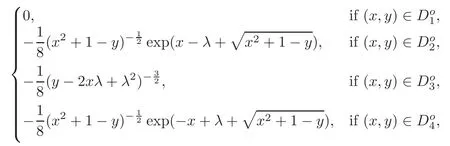
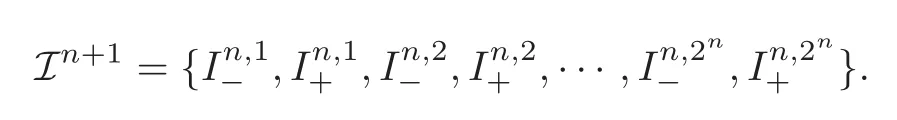
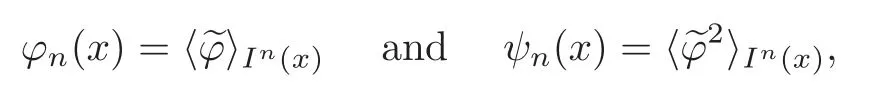
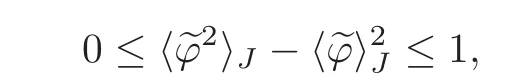
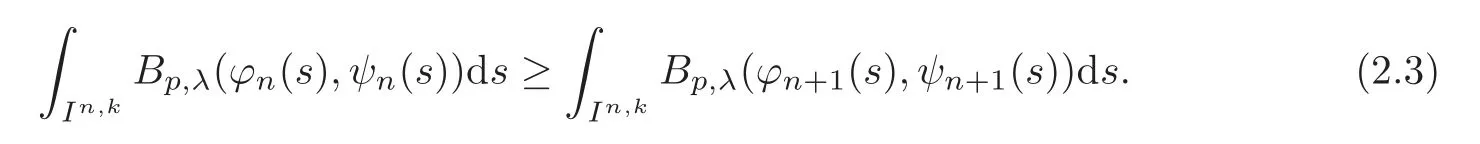
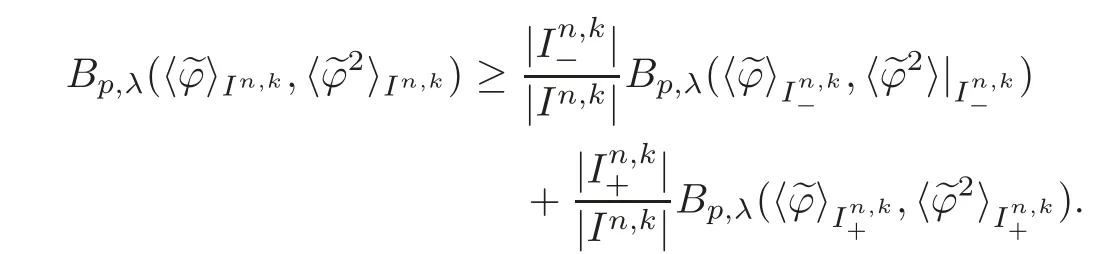
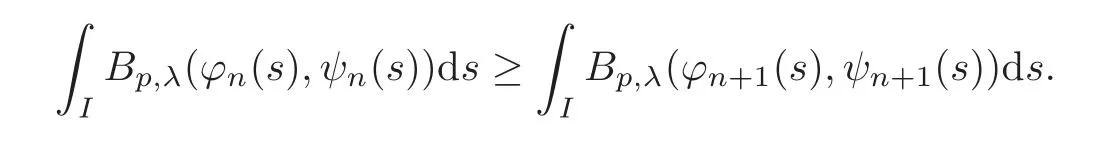
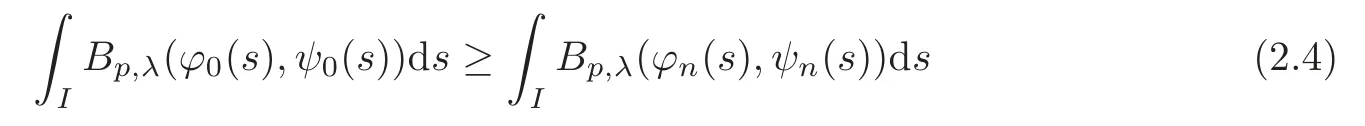
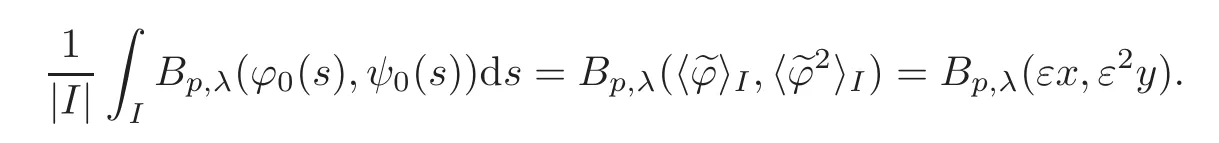
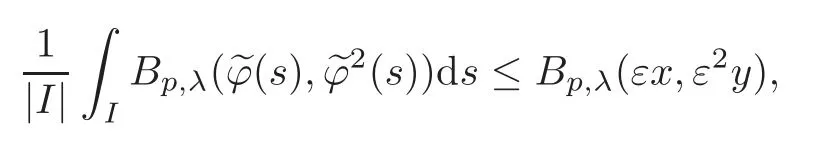
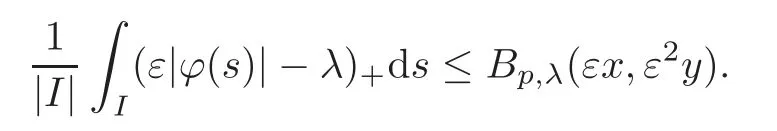
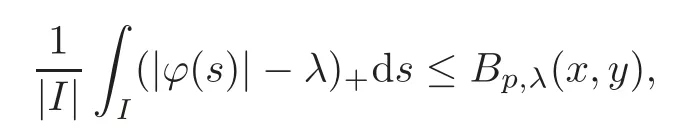
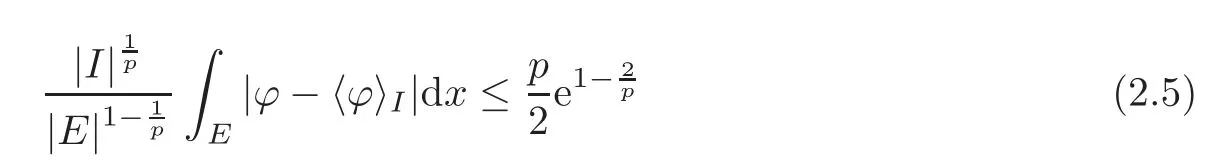
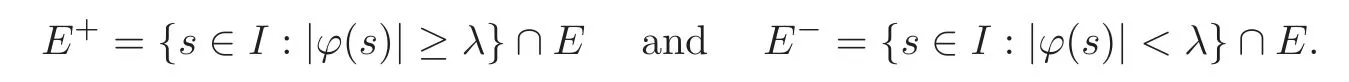
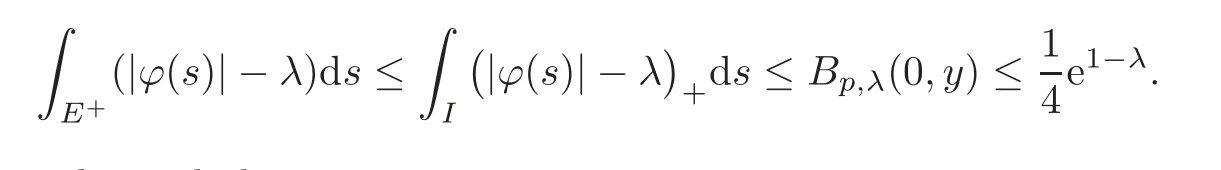
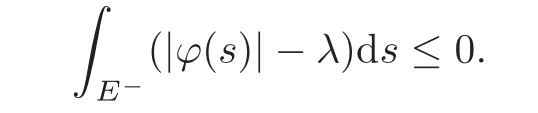
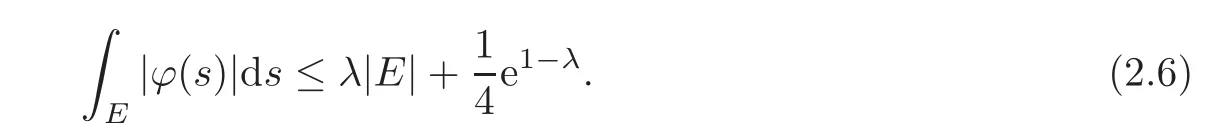
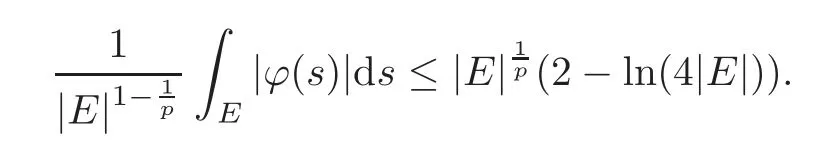
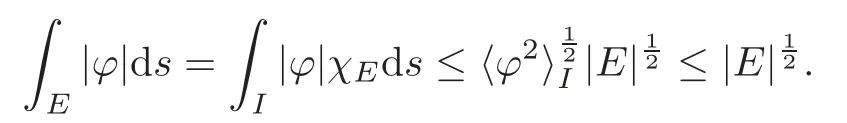

3 Sharpness
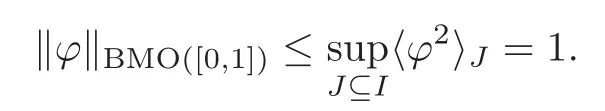
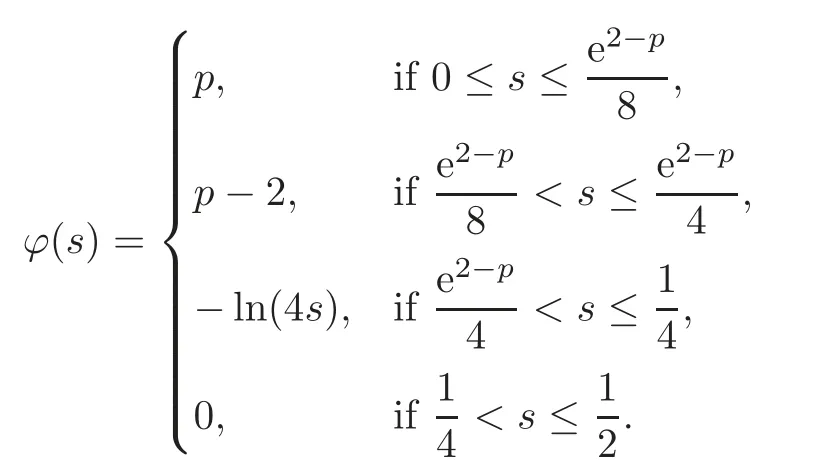
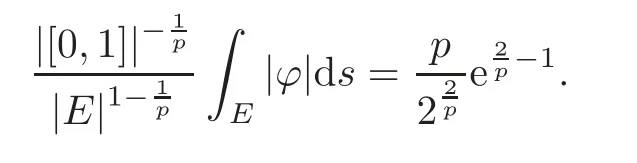

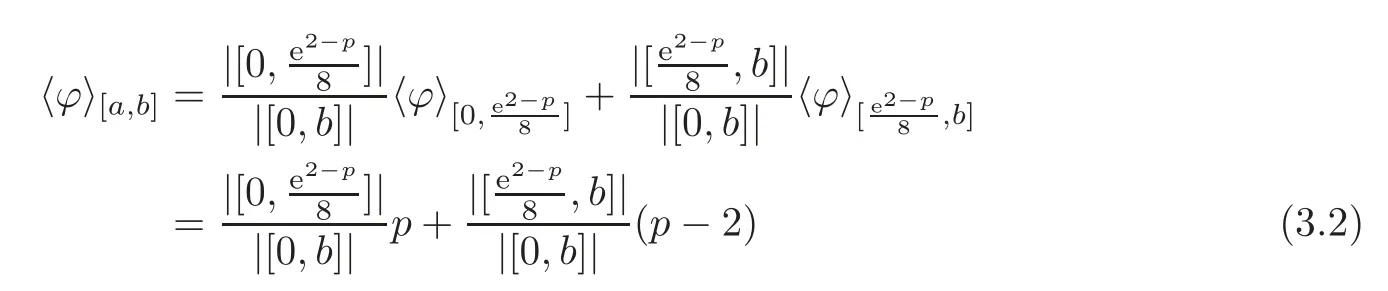
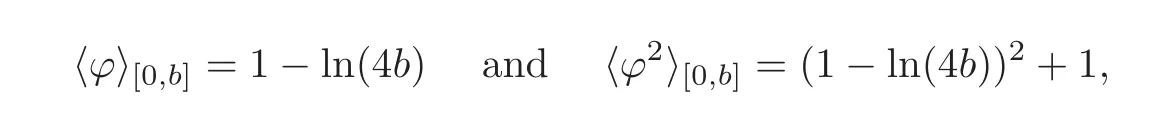
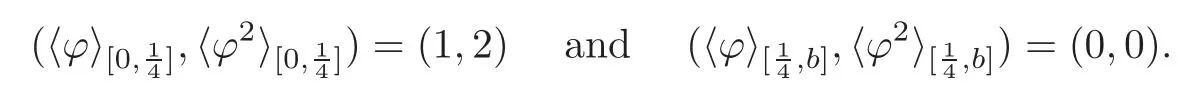
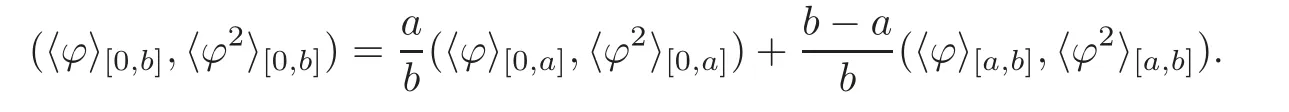
 Chinese Annals of Mathematics,Series B2015年2期
Chinese Annals of Mathematics,Series B2015年2期
