Bo HOU Suogang GAO

1 Introduction

Throughout this paper,C denotes the field of complex numbers and R denotes the field of real numbers.

In[20],Hartwig and Terwilliger found a presentation for the three-pointsl2loop algebra via generators and relations.To obtain this presentation,they defined a Lie algebraby generators and relations,and displayed an isomorphism fromto the three-pointsl2loop algebra.In[15],Elduque found an attractive decomposition ofinto a direct sum of three abelian subalgebras,and showed how these subalgebras are related to the Onsager subalgebras.In[19],Hartwig classified the finite-dimensional irreducible-modules over an algebraically closed field F with characteristic 0.In[22],Itand Terwilliger described the finite-dimensional irreducible-modules from multiple points of view.

LetDbe an integer at least 3 and letH(D,2)denote the hypercube.It is known thatH(D,2)is aQ-polynomial distance-regular graph with diameterD,and its eigenvalue sequence and its dual eigenvalue sequence are allIn this paper,we display an action ofon the standard moduleVofH(D,2).To describe this action we define six matrices in MatX(C),called

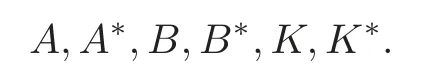
Moreover,for each matrix above we compute the transpose and then compute the transpose of each generator ofonV.

2 Tetrahedron Algebraand Onsager Algebra O

In this section,we recall the definitions of the tetrahedron algebraand the Onsager algebraOand show how the finite-dimensional irreducible modules forandOare related.

Definition 2.1(see[20,Definition 1.1])Letdenote the Lie algebra overCwith generators

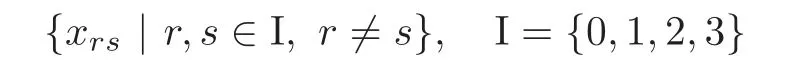
and the following relations:

(i)For all distinct r,s∈I,

(ii)For all mutually distinct r,s,t∈I,

(iii)For all mutually distinct r,s,t,u∈I,

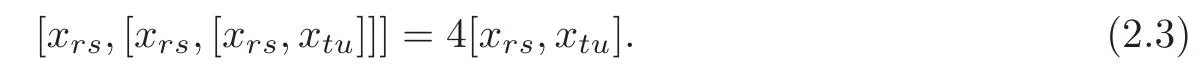
We callthe tetrahedron algebra.

Remark 2.1(2.3)is the Dolan-Grady relation.

Definition 2.2(see[19,Definition 1.2])Let O denote the Lie algebra overCwith generators X,Y satisfying relations

We call O the Onsager algebra.We call X,Y the standard generators for O.

Proposition 2.1(see[20,Proposition 4.7])Let r,s,t,u denote mutually distinct elements ofI.Then there exists a unique Lie algebra homomorphism from O tothat sends

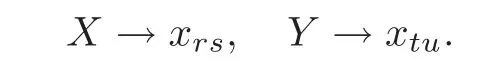
Note 2.1(see[20,Note 4.8])The homomorphism in Proposition 2.1 is an injection.

LetVdenote a finite-dimensional irreducibleO-module.Then by[19,Theorem 2.4],the standard generatorsX,Yare diagonalizable onV.Moreover,there exist an integerd≥0 and scalarsα,α?∈C such that the set of distinct eigenvalues ofX(resp.Y)onVis{d?2i+α|0≤i≤d}(resp.{d?2i+α?|0≤i≤d}).We call the ordered pair(α,α?)the type ofV.ReplacingX,YbyX?αI,Y?α?I,respectively,the type becomes(0,0).LetVdenote a finite-dimensional irreducible-module.Then by[19,Theorem 3.8],each generatorxrsofis diagonalizable onV.Moreover,there exists an integerd≥0 such that the set of distinct eigenvalues ofxrsonVis{d?2i|0≤i≤d}.We calldthe diameter ofV.The finite-dimensional irreducible modules forandOare related according to the following two propositions and the subsequent remark.

Proposition 2.2(see[19,Theorem 1.7])Let V denote a finite-dimensional irreduciblemodule.Then there exists a unique O-module structure on V such that the standard generators X,Y act on V as x01,x23respectively.This O-module structure is irreducible and has type(0,0).

Proposition 2.3(see[19,Theorem 1.8])Let V denote a finite-dimensional irreducible O-module of type(0,0).Then there exists a unique-module structure on V such that the standard generators X,Y act on V as x01,x23respectively.This-module structure is irreducible.

Remark 2.2(see[19,Remark 1.9])Combining the previous two propositions,we obtain a bijection between the following two sets:

(i)The isomorphism classes of finite-dimensional irreducibleO-modules of type(0,0).

(ii)The isomorphism classes of finite-dimensional irreducible-modules.

3 Terwilliger Algebra of a Distance-Regular Graph

In this section,we review some definitions and basic results concerning the distance-regular graphs.For more background information,we refer the readers to[1,3,18,29].

LetXdenote a nonempty finite set.Let MatX(C)denote the C-algebra consisting of all matrices whose rows and columns are indexed byXand whose entries are in C.LetV=CXdenote the vector space over C consisting of column vectors whose coordinates are indexed byXand whose entries are in C.We observe that MatX(C)acts onVby left multiplication.We callVthe standard module.We endowVwith the Hermitian inner productthat satisfiesu,v=foru,v∈V,wheretdenotes transpose and?denotes complex conjugation.For ally∈X,letdenote the element ofVwith 1 inycoordinate and 0 in all other coordinates.We observe that{|y∈X}is an orthonormal basis forV.

Let Γ=(X,R)denote a finite,undirected,connected graph,without loops or multiple edges,but with a vertex setXand an edge setR.Let?denote the path-length distance function for Γ,and setD:=max{?(x,y)|x,y∈X}.We callDthe diameter of Γ.We say Γ is distance-regular whenever for all integersh,i,j(0≤h,i,j≤D)and for all verticesx,y∈Xwith?(x,y)=h,the number

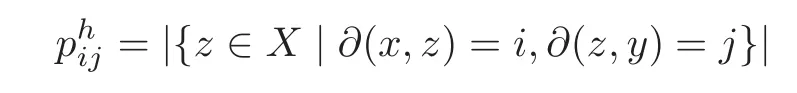
is independent ofxandy.Theare called the intersection numbers of Γ.

For the rest of this paper,we assume that Γ is a distance-regular graph with diameterD≥3.

We mention a fact for later use.By the triangle inequality,for 0≤h,i,j≤D,we have(resp.),whenever one ofh,i,jis greater than(resp.equal to)the sum of the other two.

We recall the Bose-Mesner algebra of Γ.For 0≤i≤D,letAidenote the matrix in MatX(C)with the(x,y)-entry:

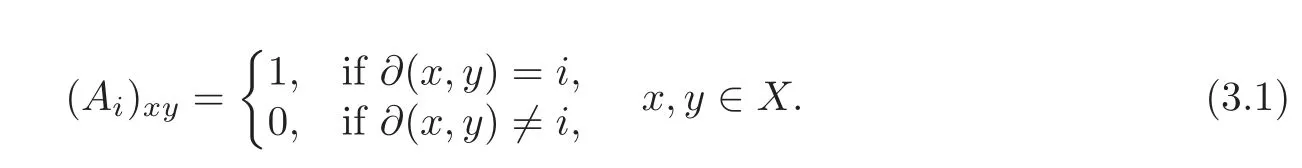
We callAitheith distance matrix of Γ.The matrixA1is often called the adjacency matrix of Γ. We observe that(i)A0=I;(v)whereI(resp.J)denotes the identity matrix(resp.all 1s matrix)in MatX(C).Using these facts,we find thatA0,A1,···,ADform a basis for a commutative subalgebraMof MatX(C).We callMthe Bose-Mesner algebra of Γ.It turns out thatA1generatesM(see[1,p.190]).By[3,p.45],Mhas a second basisE0,E1,···,EDsuch that(i)E0=|X|?1J;(iii)=Ei(0≤i≤D);(iv(v)EiEj=δijEi(0≤i,j≤D).We callE0,E1,···,EDthe primitive idempotents of Γ.

We recall the eigenvalues of Γ.SinceE0,E1,···,EDform a basis forM,there exist complex scalarsθ0,θ1,···,θDsuch thatObserve thatA1Ei=EiA1=θiEifor 0≤i≤D.By[1,p.197],the scalarsθ0,θ1,···,θDare in R.Observe thatθ0,θ1,···,θDare mutually distinct sinceA1generatesM.We callθithe eigenvalue of Γ associated withEi(0≤i≤D).Observe that

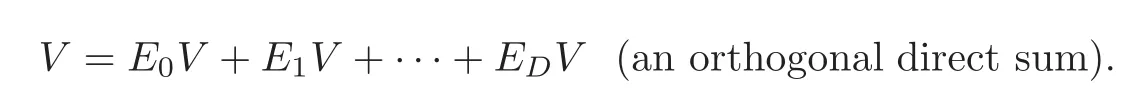
For 0≤i≤D,the spaceEiVis the eigenspace ofA1associated withθi.

We now recall the Krein parameters.Let?denote the entrywise product in MatX(C).Observe thatAi?Aj=δijAifor 0≤i,j≤D,soMis closed under?.Thus,there exist complex scalars(0≤h,i,j≤D)such that

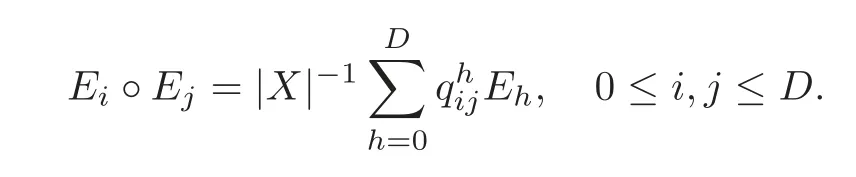
Byis real and nonnegative for 0≤h,i,j≤D.Theare called the Krein parameters of Γ.The graph Γ is said to beQ-polynomial(with respect to the given orderingE0,E1,···,EDof the primitive idempotents)whenever for 0≤h,i,j≤D,(resp.whenever one ofh,i,jis greater than(resp.equal to)the sum of the other two(see[4,p.235]).See[3,5–7,10,12–13,26]for the background information on theQ-polynomial property.

For the rest of this section,we assume Γ is aQ-polynomial distance-regular graph with respect toE0,E1,···,ED.

We recall the dual Bose-Mesner algebra of Γ.For the rest of this paper,we fix a vertexx∈X.We viewxas a“base vertex”.For 0≤i≤D,letdenote the diagonal matrix in MatX(C)with the(y,y)-entry

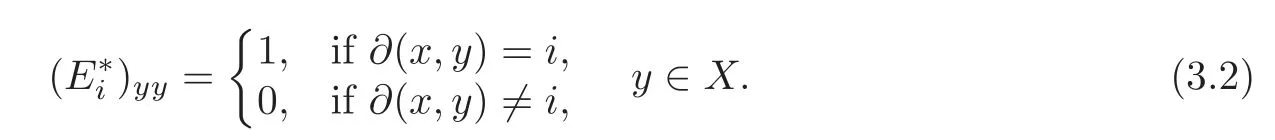
We calltheith dual idempotent of Γ with respect tox(see[28,p.378]).We observe that(i)=I;(ii)(0≤i≤D);(iii)(0≤i≤D);(iv)(0≤i,j≤D).By these facts,form a basis for a commutative subalgebraM?of MatX(C).We callM?the dual Bose-Mesner algebra of Γ with respect tox(see[28,p.378]).For 0≤i≤D,letdenote the diagonal matrix in MatX(C)with(y,y)-entryfory∈X.Thenis a basis forM?(see[28,p.379]).Moreover,(i)(0≤i≤D);(iii)(0≤i≤D);(iv)(0≤i,j≤D)(see[28,p.379]).We callthe dual distance matrices of Γ with respect tox.The matrixis often called the dual adjacency matrix of Γ with respect tox.The matrixgenerates(see[28,Lemma 3.11]).

We recall the dual eigenvalues of Γ.Sinceform a basis forM?,there exist complex scalarssuch thatObserve thatfor 0≤i≤D.By[28,Lemma 3.11],the scalarsare in R.Observe thatare mutually distinct sincegeneratesM?.We callthe dual eigenvalue of Γ associated with(0≤i≤D).

We recall the subconstituents of Γ.From(3.2)we find

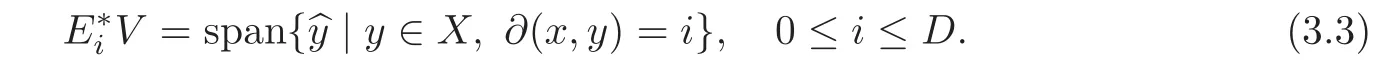
By(3.3)and since{?y|y∈X}is an orthonormal basis forV,we find

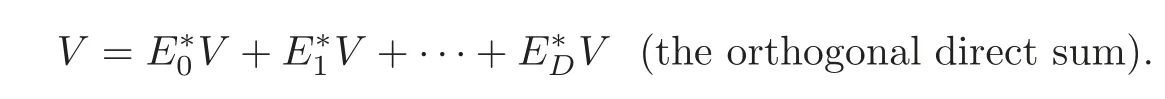
For 0≤i≤D,the spaceis the eigenspace ofassociated withWe calltheith subconstituent of Γ with respect tox.

We recall the Terwilliger algebra of Γ.LetT=T(x)denote the subalgebra of MatX(C)generated byMandM?.We callTthe Terwilliger algebra(or the subconstituent algebra)of Γ with respect tox(see[29,De finition 3.3]).We observe thatTis generated byA1,and has finite dimension.Moreover,Tis semisimple since it is closed under the conjugate transponse map(see[11,p.157]).By[29,Lemma 3.2],the following are relations inT:

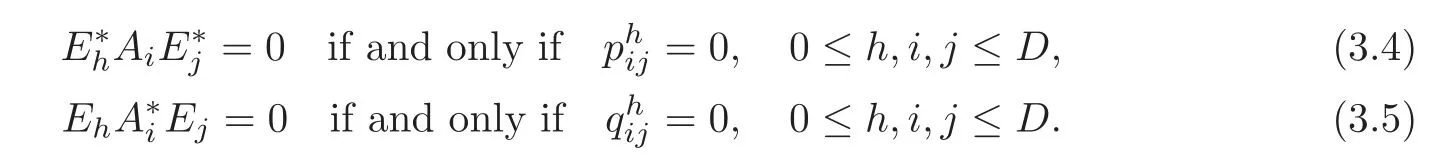
See[8–10,14,16–17,21,27–30]for more information on the Terwilliger algebra.

For the rest of this paper,we adopt the following notation convention.

Notation 3.1Assume that Γ=(X;R)is a distance-regular graph with diameterD≥3 and has aQ-polynomial structure with respect to the orderingE0,E1,···,EDof the primitive idempotents.We fixx∈Xand write(0≤i≤D),T=T(x).We use the abbreviationV=CX.

With reference to Notation 3.1,we recall some useful results onT-modules.By aT-module,we mean a subspaceW?Vsuch thatBW?Wfor allB∈T.LetWdenote aT-module and letdenote aT-module contained inW.Then the orthogonal complement ofinWis aT-module(see[17,p.802]).It follows that eachT-module is an orthogonal direct sum of irreducibleT-modules.In particular,Vis an orthogonal direct sum of irreducibleT-modules.

LetWdenote an irreducibleT-module.Observe thatWis the direct sum of the nonzero spaces amongSimilarly,Wis the direct sum of the nonzero spaces amongE0W,···,EDW.By the endpoint ofW,we mean min{i|0≤i≤D,0}.By the diameter ofW,we mean|{i|0≤i≤D,0}|?1.By the dual endpoint ofW,we mean min{i|0≤i≤D,EiW0}.By the dual diameter ofW,we mean|{i|0≤i≤D,EiW0}|?1.It turns out that the diameter ofWis equal to the dual diameter ofW(see[26,Corollary 3.3]).

Lemma 3.1(see[28,Lemmas 3.4,3.9,3.12])With reference to Notation3.1,let W denote an irreducible T-module with endpoint ρ,dual endpoint τ,and diameter d.Then ρ,τ,d are nonnegative integers such that ρ+d≤D and τ+d≤D.Moreover,the following(i)–(iv)hold:

We finish this section with a comment.

Lemma 3.2(see[23,Lemma 12.1])With reference to Notation3.1,for Y∈MatX(C),the following are equivalent:

(i)Y∈T.

(ii)Y W?W for all irreducible T-modules W.

4 Split Decompositions of Standard Module

In this section,we recall the split decompositions for the standard module and define some useful matrices by using these decompositions.

Definition 4.1(see[23,Definition 10.1])With reference to Notation3.1,for?1≤i,j≤D,we define

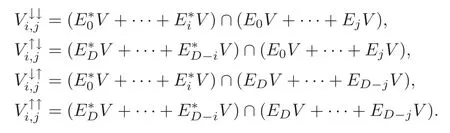
In each of the above four equations,we interpret the right-hand side as being0if i=?1or j=?1.

Definition 4.2(see[23,Definition 10.2])With reference to Notation3.1and Definition4.1,for μ,ν∈{↓,↑}and0≤i,j≤D,we haveTherefore,

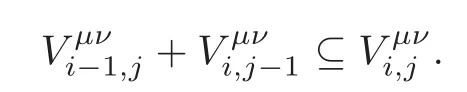
Referring to the above inclusion,we defineto be the orthogonal complement of the left-handside in the right-hand side;that is,

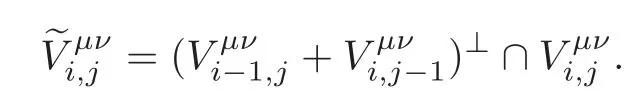
Lemma 4.1(see[23,Definition 10.3])With reference to Notation3.1and Definition4.2,we have that for μ,ν∈{↓,↑},

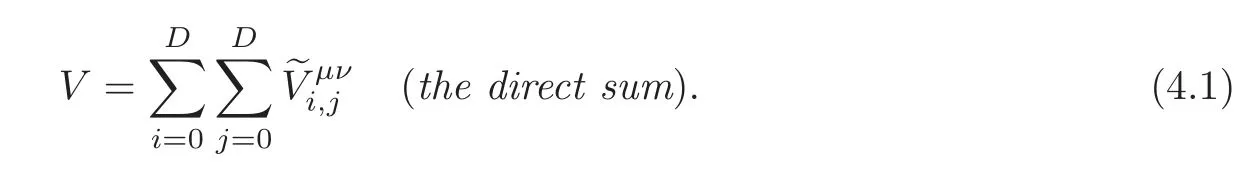
Definition 4.3(see[25,Definition 6.4])We call the sum(4.1)the(μ,ν)-split decomposition of V with respect to x.This decomposition is not orthogonal in general.

Definition 4.4(see[24,Definition 4.1])With reference to Notation3.1and Definition4.2,for μ,ν∈{↓,↑}and0≤i,j≤D,we defineMatX(C)so that

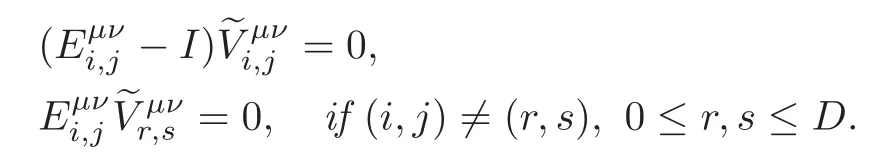
Lemma 4.2(see[24,Theorem 4.7])With reference to Notation3.1and Definition4.4,for0≤i,j≤D,

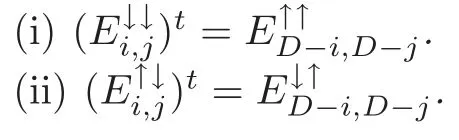
The following result on irreducibleT-modules is a mild generalization of[31,Lemma 6.1].

Lemma 4.3(see[23,Lemma 11.4])With reference to Notation3.1and Definition4.2,let W denote an irreducible T-module with the endpoint ρ,the dual endpoint τ,and the diameter d.Then the following(i)–(iv)hold for0≤i,j≤d:

(i)The space

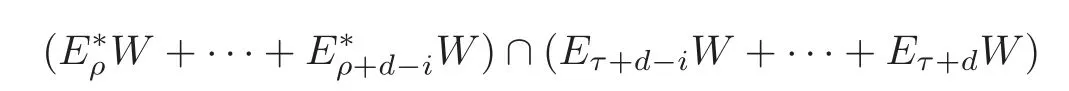
is contained in

(ii)The space

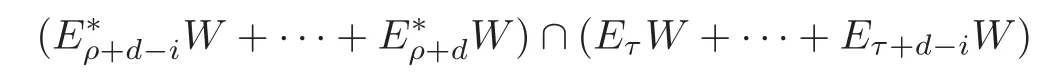
is contained in

(iii)The space

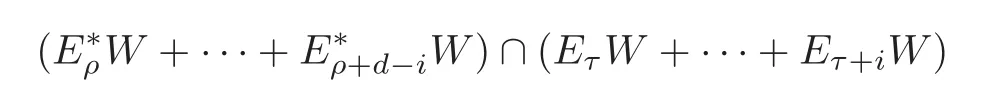
is contained in

(iv)The space

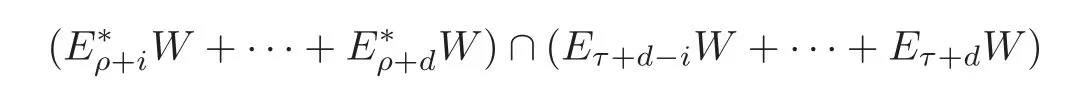
is contained in

5 Displacement Decompositions of Standard Module

In this section,we recall the displacement decompositions for the standard module and discuss their basic properties.

Definition 5.1(see[31,Definition 4.1])With reference to Notation3.1,let W denote an irreducible T-module with the endpoint ρ,the dual endpoint τ,and the diameter d.By the displacement of W of the first kind(resp.the second kind),we mean the integer ρ+τ+d?D(resp.ρ?τ).

Lemma 5.1(see[24,Corollary 3.2])With reference to Notation3.1,let W denote an irreducible T-module.Then the following hold:

(i)Let η denote the displacement of Wof the first kind.Then0≤η≤D.

(ii)Let ζ denote the displacement of Wof the second kind.Then?D≤ζ≤D.

Definition 5.2(see[31,Definitions 4.3,4.5])With reference to Notation3.1,for0≤η≤D,let Vηdenote the subspace of V spanned by the irreducible T-modules,for which η is the displacement of the first kind.Observe that Vηis a T-module.By[31,Lemma4.4],we have

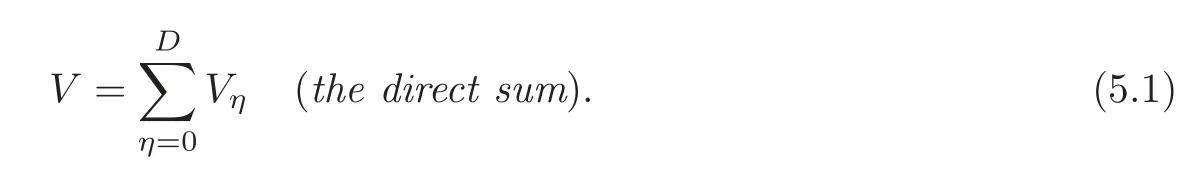
We call the sum(5.1)the displacement decomposition of V of the first kind with respect to x.

Definition 5.3(see[24,Definitions 3.7,3.9])With reference to Notation3.1,for?D≤ζ≤D,let Vζdenote the subspace of V spanned by the irreducible T-modules,for which ζ is the displacement of the second kind.Observe that Vζis a T-module.By[24,Lemma3.8],we have

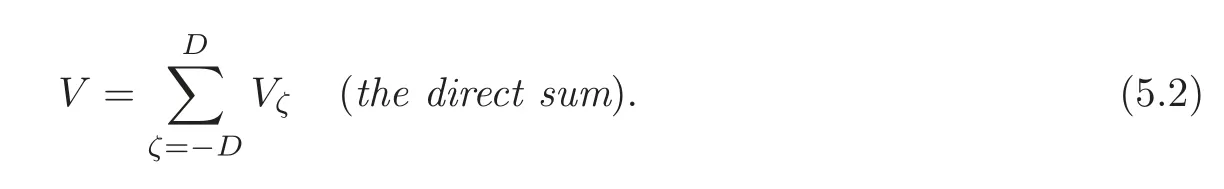
We call the sum(5.2)the displacement decomposition of V of the second kind with respect to x.

Lemma 5.2(see[24,Theorem 3.20])With reference to Notation3.1and Definitions4.2and5.2,thellowing hold for0≤η≤D:

(i)where the sum is over all ordered pairs i,j such that0≤i,j≤D andi+j=D+η.

(ii)where the sum is over all ordered pairs i,j such that0≤i,j≤D andi+j=D?η.

Lemma 5.3(see[24,Theorem 3.21])With reference to Notation3.1and Definitions4.2and5.3,the following hold for?D≤ζ≤D:

(i)where the sum is over all ordered pairs i,j such that0≤i,j≤D andi+j=D+ζ.

(ii)where the sum is over all ordered pairs i,j such that0≤i,j≤D andi+j=D?ζ.

6 Hypercube H(D,2)and Matrices A,A?,B,B?,K,K?

In this section,we recall some facts concerning the hypercube,and define some useful matrices by using its split decompositions.

Definition 6.1Let D denote a positive integer,and let{1,?1}Ddenote the set of sequences?1?2···?D,where?i∈{1,?1}for1≤i≤D.We let H(D,2)denote the graph with a vertex set

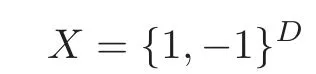
and an edge set

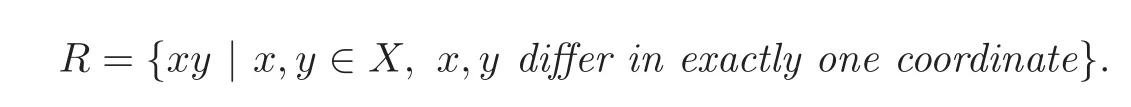
We refer to H(D,2)the hypercube.H(D,2)is also known as a D-cube or a Hamming cube.

For the rest of this paper,we always assume that the diameterDof the hypercubeH(D,2)is at least 3.

Definition 6.2For the hypercube H(D,2),let E0,E1,···,EDdenote the primitive idempotents and let A be the adjacency matrix.Let V be the standard module.Fix a vertex x∈Xof H(D,2).Letdenote the dual primitive idempotents with respect to x and letA?be the dual adjacency matrix with respect to x.Let T be the Terwilliger algebra with respect to x.

Lemma 6.1With reference to Definition6.2,the hypercube H(D,2)is a Q-polynomial distance-regular graph whose eigenvalue sequence and dual eigenvalue sequence are all{D?Moreover,the space EiV(resp.)is the eigenspace of A(resp.A?)associated withthe eigenvalue D?2i for0≤i≤D.

ProofImmediate from[3,p.261]and[16,Theorems 3.7,12.1].

Lemma 6.2With reference to Definition6.2,the matrices A and A?satisfy the Dolan-Grady relations

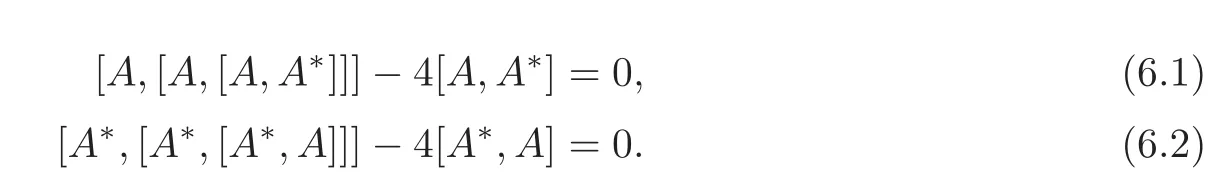
ProofImmediate from[16,Theorem 4.2].

Lemma 6.3(see[16,Theorems 6.1,8.1])With reference to Definition6.2,let W denote an irreducible T-module with the endpoint ρ,the dual endpoint τ,and the diameter d.Then the endpoint and the dual endpoint are equal.Moreover,we have

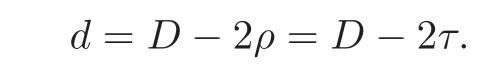
Corollary 6.1With reference to Definition6.2,let W denote an irreducible T-module.Then the displacements of Wof the first kind and the second kind are zero.

ProofImmediate from Definition 5.1 and Lemma 6.3.

Lemma 6.4With reference to Definitions4.2,4.4and6.2,for μ,ν∈{↓,↑}and0≤i,j≤D,we haveandunless i+j=D.

ProofFrom Lemmas 5.2 and 5.3 and Corollary 6.1,forμ,ν∈{↓,↑}and 0≤i,j≤D,we haveunlessi+j=D.Then by Definition 4.4,we haveunlessi+j=D.

Corollary 6.2With reference to Definitions4.2and6.2,the following holds for μ,ν∈{↓,↑}:

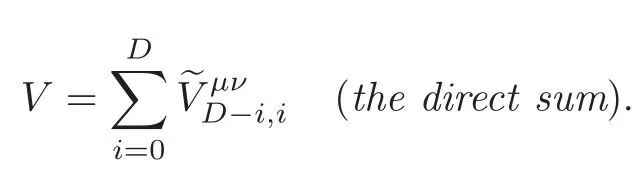
ProofImmediate from Lemmas 4.1 and 6.4.

Definition 6.3With reference to Definitions4.2and6.2,by Corollary6.2we define B,B?,K,K?to be the unique matrices inMatX(C),which satisfy the requirements of the following Table1for0≤i≤D.

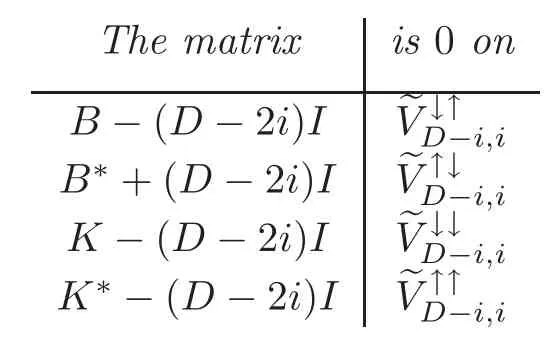
Table 1

Lemma 6.5With reference to Definitions4.4and6.3,the following(i)–(iv)hold:

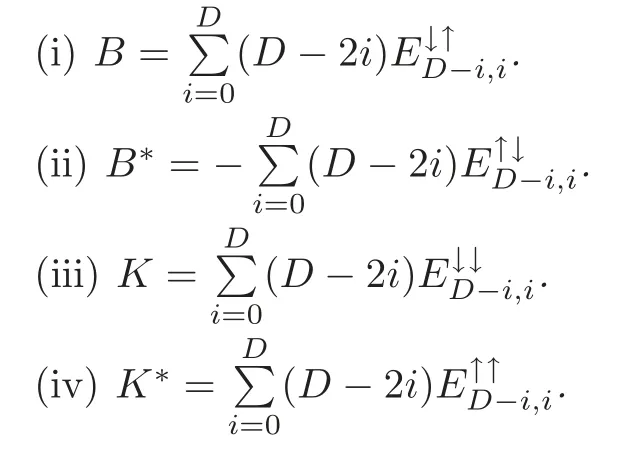
ProofImmediate from Definitions 4.4 and 6.3 and Corollary 6.2.

Lemma 6.6With reference to Definitions6.2and6.3,the following(i)–(iv)hold:

(i)A is symmetric.

(ii)A?is symmetric.

(iii)Bt=B?.

(iv)Kt=?K?.

Proof(i)–(ii)are from the definitions ofAandA?.

(iii)Combining Lemma 4.2(ii)and Lemma 6.5(i)–(ii),we have

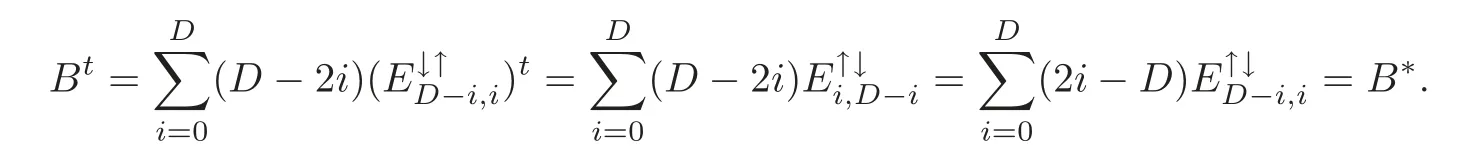
(iv)Combining Lemma 4.2(i)and Lemma 6.5(iii)–(iv),we have

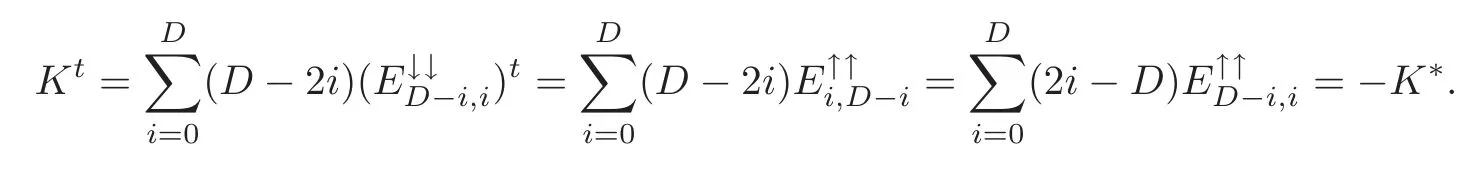
7 An Action ofon the Standard Module of H(D,2)

In this section,we continue our discussion for the hypercubeH(d,2),and state our main result of this paper,in which we will display an action ofon the standard moduleVofH(D,2).

Lemma 7.1With reference to Definitions2.1and6.2,let Wdenote an irreducible T-module with the endpoint ρ,and recall that W has diameter d=D?2ρ.Then there exists a unique-module structure on W such that the generators x01and x23act as A and A?,respectively.This-module structure is irreducible.

ProofThe matricesAandA?satisfy the Dolan-Grady relations(6.1)and(6.2)by Lemma 6.2.Therefore,there exists anO-module structure onWsuch that the standard generators act asAandA?,respectively.TheO-moduleWis irreducible sinceAandA?generateTand theT-moduleWis irreducible.By Lemmas 3.1 and 6.1,and since the endpoint and the dual endpoint ofWare equal,the actions ofAandA?onWare semisimple with the same eigenvaluesD?2ρ?2i(0≤i≤d).Therefore,by Lemma 6.3,the actions ofAandA?onWare semisimple with the same eigenvaluesd?2i(0≤i≤d).Thus,theO-moduleWhas type(0,0).So far we have shown that theO-moduleWis irreducible and has type(0,0).Combining this with Proposition 2.3,we obtain the result.

Lemma 7.2With reference to Definitions2.1and6.2,let W denote an irreducible T-module with the endpoint ρ,and recall that W has diameter d=D?2ρ.Consider the-module structure on W from Lemma7.1.For each generator xrsofand for0≤i≤d,the eigenspace of xrson W associated with the eigenvalue d?2i is given in the following Table2.

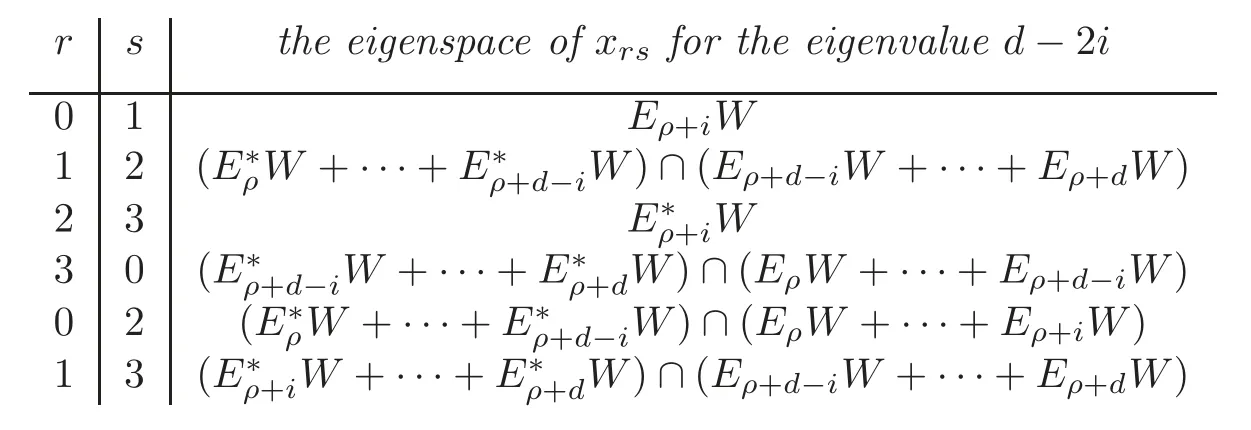
Table 2

ProofReferring to the table,we first verify row(r,s)=(0,1).By Lemma 7.1,the generatorx01acts onWasA.By Lemma 3.1(iii)–(iv)and Lemma 6.1,the spaceEρ+iWis the eigenspace ofAonWfor the eigenvalueD?2ρ?2i.By these comments and Lemma 6.3,the spaceEρ+iWis the eigenspace ofx01onWfor the eigenvalued?2i.We have verified row(r,s)=(0,1).Next,we verify row(r,s)=(2,3).By Lemma 7.1,the generatorx23acts onWasA?.By Lemma 3.1(i)–(ii)and Lemma 6.1 the spaceis the eigenspace ofA?onWfor the eigenvalueD?2ρ?2i.By these comments and Lemma 6.3,the spaceWis the eigenspace ofx23onWfor the eigenvalued?2i.We have verified row(r,s)=(2,3).The remaining rows are valid by[19,Lemma 5.7].

Lemma 7.3With reference to Definitions2.1and6.2–6.3,let W denote an irreducible T-module with the endpoint ρ,and recall that W has diameter d=D?2ρ.Consider the?-module structure on W from Lemma7.1.In Table3below,each row contains an element of?and a matrix inMatX(C).The actions of these two objects on W coincide.

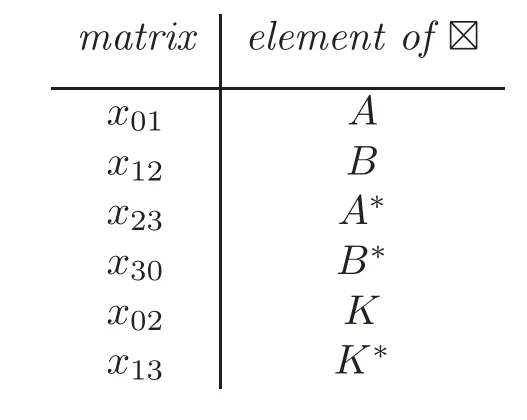
Table 3

ProofBy Lemma 7.1,the expressionsA?x01andA??x23are all 0 onW.Next,we show thatB?x12is 0 onW.To this end,we pickw∈Wand show

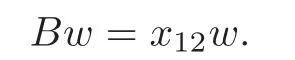
Recall thatx12is semisimple onWwith eigenvaluesd?2i(0≤i≤d).Therefore,without loss of generality,we may assume that there exists an integeri(0≤i≤d)such thatx12w=(d?2i)w.By row(r,s)=(1,2)in Table 2 of Lemma 7.2 and by Lemma 4.3(i)and Lemma 6.3,we findBy this and the first row in the table of Definition 6.3 we find

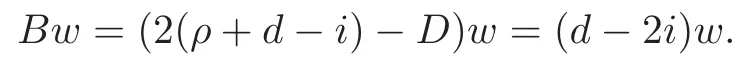
So we findBw=x12was desired.Similarly,by rows(r,s)=(3,0),(0,2),(1,3)in Table 2 of Lemma 7.2 and by Lemma 4.3(ii)–(iv),one can show that each ofB??x30,K?x02andK??x13is 0 onW.The results follow.

Theorem 7.1With reference to Definitions2.1and6.2–6.3,there exists a?-module structure on V such that the generators xijact as follows(see Table4).

Table 4

ProofNote that the standard moduleVdecomposes into a direct sum of irreducibleT-modules.Since each irreducibleT-module in this decomposition supports a-module structure from Lemma 7.1,the assertion holds by Lemma 7.3.

Theorem 7.2With reference to Definitions2.1and6.2,the following hold on V

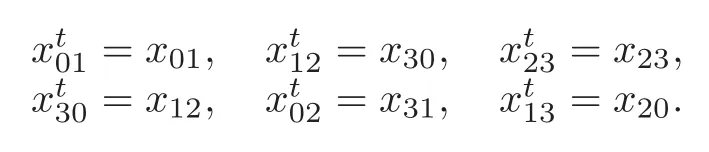
ProofImmediate from Definition 2.1,Lemma 6.6 and Theorem 7.1.

LetU()denote the universal enveloping algebra of.In Theorem 7.1 we displayed an action ofon the standard module ofV;observe that this action induces a C-algebra homomorphism fromU()to MatX(C)which we will denote by?.Now we clarify how the image?(U())is related to the Terwilliger algebraT.

Theorem 7.3With reference to Definition6.2,then T is equal to the image ?(U)).

ProofNote thatTis generated byA,A?and?(U())is generated byA,A?,B,B?,K,K?.To prove that the two subalgebras of MatX(C)are equal,it suffices to verify that each ofB,B?,K,K?is contained inT.Clearly those follow from Lemma 3.2 and Lemma 7.3.

AcknowledgementsThe authors would like to thank the referee for many valuable comments and useful suggestions.The authors are also grateful to Prof.Terwilliger P.and Prof.It?o T.for the advice they offered in their study of theq-tetrahedron algebra.

[1]Bannai,E.and It?o,T.,Algebraic Combinatorics I:Association Schemes,Benjamin/Cummings,London,1984.

[2]Biggs,N.,Algebraic Graph Theory,Cambridge University Press,Cambridge,1993.

[3]Brouwer,A.E.,Cohen,A.M.and Neumaier,A.,Distance-Regular Graphs,Springer-Verlag,Berlin,1989.

[4]Brouwer,A.E.,Godsil,C.D.,Koolen,J.H.,et al,Width and dual width of subsets in polynomial association schemes,J.Combin.Theory,Ser.A,102,2003,255–271.

[5]Caughman IV,J.S.,Spectra of bipartiteP-andQ-polynomial association schemes,Graphs Combin.,14,1998,321–343.

[6]Caughman IV,J.S.,The Terwilliger algebras of bipartiteP-andQ-polynomial association schemes,Discrete Math.,196,1999,65–95.

[7]Curtin,B.,2-homogeneous bipartite distance-regular graphs,Discrete Math.,187,1998,39–70.

[8]Curtin,B.,Bipartite distance-regular graphs I,Graphs Combin.,15,1999,143–158.

[9]Curtin,B.,Bipartite distance-regular graphs II,Graphs Combin.,15,1999,377–391.

[10]Curtin,B.,Distance-regular graphs which support a spin model are thin,Discrete Math.,197/198,1999,205–216.

[11]Curtis,C.and Reiner,I.,Representation Theory of Finite Groups and Associative Algebras,Interscience,New York,1962.

[12]Dickie,G.,TwiceQ-polynomial distance-regular graphs are thin,European J.Combin.,16,1995,555–560.

[13]Dickie,G.and Terwilliger,P.,A note on thinP-polynomial and dual-thinQ-polynomial symmetric association schemes,J.Algebraic Combin.,7,1998,5–15.

[14]Egge,E.,A generalization of the Terwilliger algebra,J.Algebra,233,2000,213–252.

[15]Elduque,A.,TheS4-action on the tetrahedron algebra,Proceedings of the Royal Society of Edinburgh:Section A Mathematics,Vol.137,2007,1227–1248.

[16]Go,J.T.,The Terwilliger algebra of the hypercube,European J.Combin.,23,2002,399–429.

[17]Go,J.T.and Terwilliger,P.,Tight distance-regular graphs and the subconstituent algebra,European J.Combin.,23,2002,793–816.

[18]Godsil,C.D.,Algebraic Combinatorics,Chapman and Hall Inc.,New York,1993.

[19]Harwig,B.,The tetrahedron algebra and its finite-dimensional irreducible modules,Linear Algebra Appl.,422,2007,219–235.

[20]Hartwig,B.and Terwilliger,P.,The tetrahedron algebra,the Onsager algebra,and thesl2loop algebra,J.Algebra,308,2007,840–863.

[21]Hobart,S.A.and ItT.,The structure of nonthin irreducibleT-modules:Ladder bases and classical parameters,J.Algebraic Combin.,7,1998,53–75.

[22]IT.and Terwilliger,P.,Finite-dimensional irreducible modules for the three-pointsl2loop algebra,Comm.Algebra,36,2008,4557–4598.

[23]It?o,T.and Terwilliger,P.,Distance regular graphs and theq-tetrahedron algebra,European J.Combin.,30,2009,682–697.

[24]Kim,J.,Some matrices associated with the split decomposition for aQ-polynomial distance-regular graph,European J.Combin.,30,2009,96–113.

[25]Kim,J.,A duality between pairs of split decompositions for aQ-polynomial distance-regular graph,Discrete Math.,310(12),2010,1828–1834.

[26]Pascasio,A.A.,On the multiplicities of the primitive idempotents of aQ-polynomial distance-regular graph,European J.Combin.,23,2002,1073–1078.

[27]Tanabe,K.,The irreducible modules of the Terwilliger algebras of Doob schemes,J.Algebraic Combin.,6,1997,173–195.

[28]Terwilliger,P.,The subconstituent algebra of an association scheme I,J.Algebraic Combin.,1,1992,363–388.

[29]Terwilliger,P.,The subconstituent algebra of an association scheme II,J.Algebraic Combin.,2,1993,73–103.

[30]Terwilliger,P.,The subconstituent algebra of an association scheme III,J.Algebraic Combin.,2,1993,177–210.

[31]Terwilliger,P.,The displacement and split decompositions for aQ-polynomial distance-regular graph,Graphs Combin.,21,2005,263–276.