Changmei SHI Donghe PEI

1 Introduction

Singularity theory is a young branch of analysis which currently occupies a central place in mathematics;it is the crossroads of paths leading from very abstract subjects of mathematics,such as commutation algebra,Lie group,differential geometry and topology.Moreover,singularity theory offers an extremely useful approach to most applied areas,such as differential geometry(see[1–2]),the theory of bifurcation(see[3–4])and physics(see[5]).Because every fi nitely determined germ is equivalent to its Taylor polynomial of some degree,the analysis of the conditions for a germ to be finitely determined involves the most important local aspects of the singularity theory.Therefore,the study of finite determinacy of smooth map-germs is an important subject in singularity theory,and it has been widely studied.The foundation of the study is laid in an important paper[6].In[6],Mather gave both algebraic and geometric characterizations of finitely determined germs with respect to the groupsR,L,A,CandK.There are also numerous useful results on the determinacy of germs due to Gaffney,du Pless and Wall,etc.,for instance in[7,8].

In the present paper,we shall work in the space of differentiable map-germs between Euclidean spaces with the constraint that a fixed submanifold is mapped into another fixed submanifold,and then naturally we encounter the relative map-germs.The concept of relative finite determination was introduced by Porto and Loibel[9].More recently there are more and more papers studying the notions of singularity theory in the relative case,for instance,finite determinacy,stability and universality(see[9–14]).However,the study of relative finite determinacy of map-germs is very few,and in all the references,the relative finite determinacy is only related to the Taylor polynomial at the origin of map-germs.In this paper we generalize this concept for a proper submanifold without boundary of the source space,and we call it the weak finite determination.The purpose of this paper is to obtain algebraic characterization of weak finitely determined relative map-germs with respect to two equivalent relations.The first is relative right-left equivalence,and the second is relative contact equivalence(i.e.,AS,T-equivalence andKS,T-equivalence).

The paper is organized as follows.Section 2 deals with the weak finiteAS,T-determinacy of relative map-germs.We achieve a suffcient condition to characterize weak finiteAS,T-determinacy of relative map-germs(see Theorem 2.1)and two results for estimating the precise degree of determinacy(see Theorems 2.2–2.3).In Section 3 we give a suffcient condition for a relative map-germ to be weak finitelyKS,T-determined(see Theorem 3.1).Finally,as an application,we prove thatAS,T-stable map-germs are weak(m+1)-AS,T-determined and weak(m+1)-KS,T-determined.

We shall use the notations as follows.

LetSandTbe submanifolds without boundary of Rnand Rmrespectively,both containing the origin.Since this paper is concerned with a local study,without loss of generality,we may assume that

A relative map-germf:(Rn,S)→(Rm,T)is a differential map-germ at 0∈Rnwithf(S)?Tandf(0)=0.Denote byEthe space of relative map-germs.

LetEndenote the ring of smooth function-germs at the origin in Rn,and letMndenote its unique maximal ideal.LetCS(Rn)be the local ring{f∈En:f|S≡constant},and letε(S,n)={f∈CS(Rn)|f(S)≡0},which is the maximal ideal ofCS(Rn).

For anyf∈E,it induces a homomorphismf?:CT(Rm)→CS(Rn)defined byf?(h)=h?f;this allows us to consider everyCS(Rn)-module as aCT(Rm)-module viaf?.Letf?ε(T,m)=〈f1,f2,···,ft〉be the ideal generated by the componentsf1,···,ft,and letf?(ε(T,m))denote the image ofε(T,m)underf,which is not(in general)an ideal ofCS(Rn).

Lete1,e2,···,embe the canonical basis of the vector space Rm,and they define a system of generators of theCS(Rn)-module

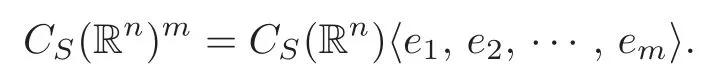
Similarly,we haveε(S,n)m=ε(S,n)〈e1,e2,···,em〉.

LetRdenote the group of germs at the origin of local diffeomorphisms of Rn,and letRS(n)={φ∈R:φ|S≡idS},where id denotes the identity.We also observe thatRS(n)is a subgroup ofR.

Now,letAS,T=RS(n)×RT(m)denote the relative right-left equivalent group,and let

KS,T={(M,h)|M:(Rn,0)→(GL(m,R),M(0))is aC∞map-germ,h∈RS(n)}denote the relative contact equivalent group.

The two groups act onEin the following way:

Iff∈E,(φ,ψ)∈AS,Tand(M,h)∈KS,T,then(φ,ψ)·fand(M,h)·fare defined respectively by

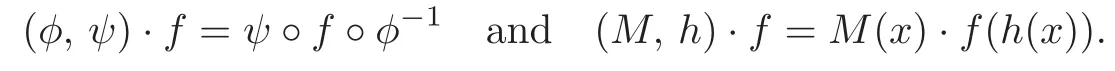
LetGbe a group which acts onE.

Definition 1.1(see[8])Two relative map-gems f,g are called G-equivalent if f and g belong to the same orbit of G on E.

Forf,g∈E,we say thatfandghave the samek-jet atSifghas the samek-jet asfat each point ofS.We writejkffor thek-jet atSoff.

Definition 1.2A relative map-germ f is called weak k-G-determined if every relative mapgerm having the same k-jet at S as f is G-equivalent to f.If f is weak k-G-determined for some k＜∞,then it is weak finitely G-determined,and the least such k is the degree of determinacy.

Remark 1.1(i)IffandgareAS,T-equivalent,thenf|S=g|S,that is,the value of a germ atSis an invariant of the action ofAS,T.SetEf={g∈E:f|S=g|S}.

(ii)Takings=nandt=m,thenS=T={0}.In this case,the weakG-determinacy actually is theG-determinacy.

2 Weak Finite AS,T-Determinacy of Relative Map-Germs

Definition 2.1(see[10])Let f∈E be a relative map-germ.We define

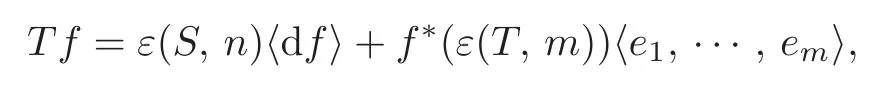
where

In addition,denote

Definition 2.2(see[10])Let F:(Rp×Rn,Rp×S)→(Rp×Rm,Rp×T)be a germ of the form F(t,x)=(t,f(t,x)).Then we say that F is a p-parameter unfolding of f0:(Rn,S)→(Rm,T),if f(0,x)=f0(x)and f(t,x)=f(0,x)for all t∈Rpand x∈S.

In order to characterize weak finiteAS,T-determinacy for relative map-germs,we need the following lemmas which can be obtained in a similar way as[6].So these results are stated without proofs here.

Lemma 2.1Suppose that g has the same k-jet at S as f.Then

(1)

(2)

where εk(S,n)denotes the k-th power of ε(S,n).

Lemma 2.2Let F,G:(R×Rn,R×S)→(R×Rm,R×T)be level preserving C∞map-germs such that G?F∈ε?(S,n)·CR×S(R×Rn)m.Then

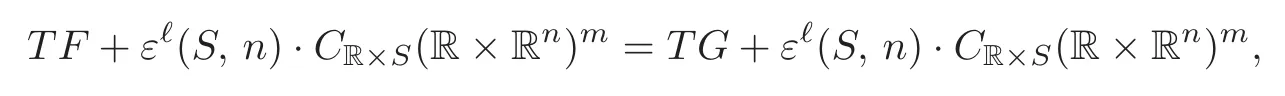
where TF=ε(R×S,1+n)〈dft(x)〉+F?(ε(R×T,1+m))〈e1,···,em〉and F(t,x)=(t,ft(x)).

Lemma 2.3Let F0(t,x)=(t,f(x))be the constant unfolding of f.Then ε?(S,n)·CS(Rn)m?Tf if and only if ε?(S,n)·CR×S(R×Rn)m?TF0.

Lemma 2.4(see[10])Let F(t,x)=(t,f(t,x))be a one-parameter unfolding of f0.ThenF is trivial if and only if

Lemma 2.5Let f be a relative map-germ,A and B be a finitely generated CS(Rn)-module and a CT(Rm)-module respectively,and M?CS(Rn)be a finitely generated ideal.If B?f?ε(T,m)·A,then M·A?B+M2·A implies M·A?B.

Lemma 2.6(see[15])Let h:U→U′be a G-submersion,where G is a Lie group.Let u′∈U′and V=h?1(u′).Suppose that V is connected.Then the necessary and suffcient condition for V to be contained in a single orbit of G is that

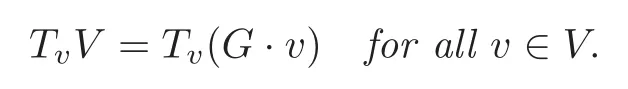
Lemma 2.7Let F:(R×Rn,R×S)→(R×Rm,R×T)be given by F(t,x)=(t,ft(x)),which is a C∞level preserving map-germ.Then each germ fthas the same k-jet at S if and only if

Lemma 2.8Let f∈E and V={g∈Ef|jkg=jkf}.Then

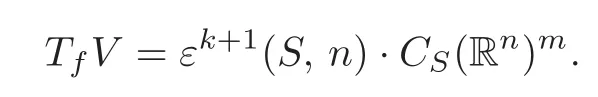
Theorem 2.1Let f∈E.If εk+1(S,n)·CS(Rn)m?Tf,then f is weak(2k+1)-AS,T-determined.

ProofLetg∈Efsuch thatj?g=j?f,where?=2k+1.Let

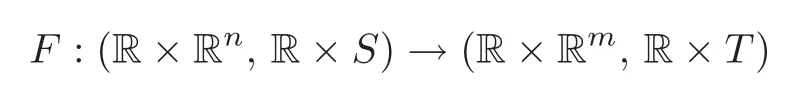
be given byF(t,x)=(t,ft(x)),whereft(x)=(1?t)f(x)+tg(x).SoFis a level preservingC∞map-germ withf0(x)=f(x)andf1(x)=g(x).To prove thatfisAS,T-equivalent tog,it is enough to show thatFis a trivial unfolding off.However,by using the assumption thatfandghave the same?-jet atS,we get

According to Lemma 2.4,it suffces to prove that

The hypothesis in the theorem gives

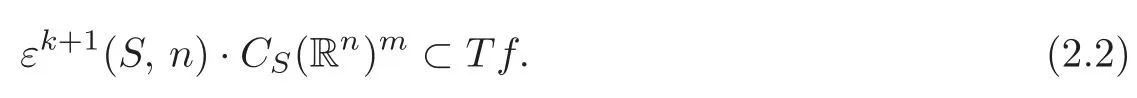
By Lemma 2.1,we have

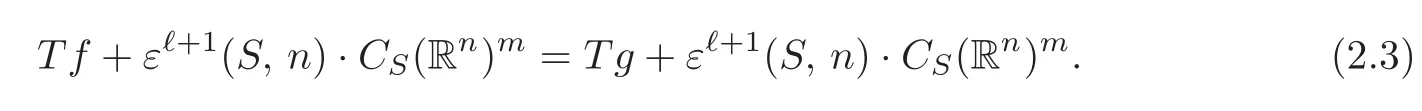
So

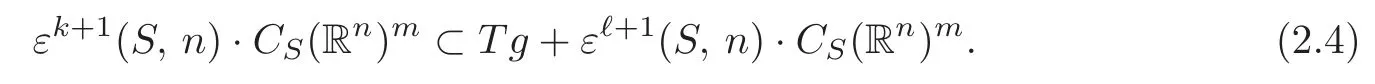
Set

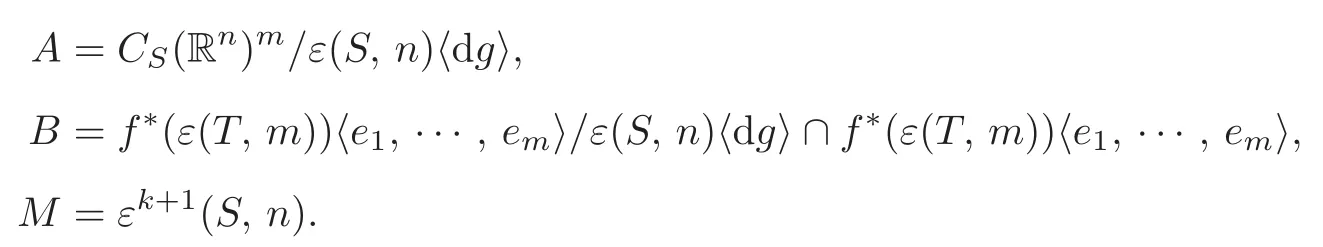
ThenAis a finitely generatedCS(Rn)-module,Bis a finitely generatedCT(Rm)-module,andMis an ideal ofCS(Rn).Note that

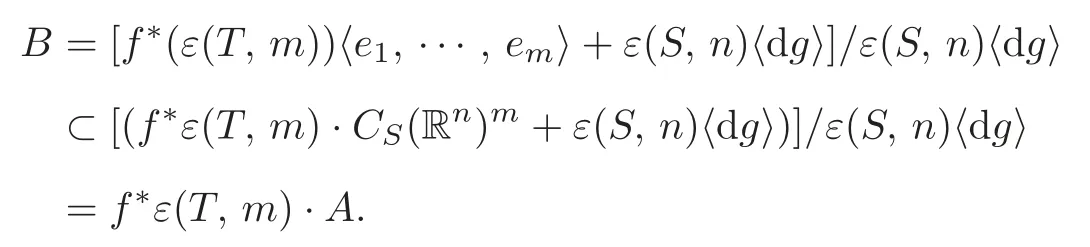
From(2.4)we get

Thus(2.5)impliesM·A?Bby Lemma 2.5.This shows that

Since each germfthas the same?-jet atSasf,it follows that

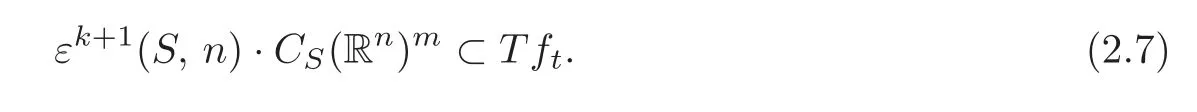
For fixedt0∈R,we letFt0(t,x)=(t,ft0(x)).Applying Lemma 2.3 and(2.7),we get

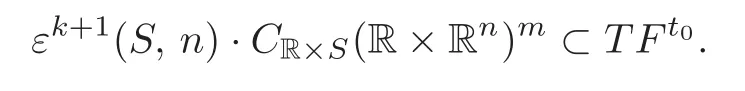
F(t,x)?Ft0(t,x)=(0,(t?t0)[g(x)?f(x)]),then

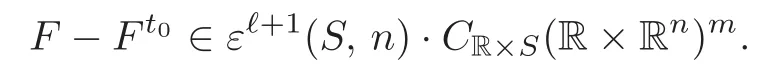
Thus,

and we again use the algebraic argument as(2.6)to conclude that

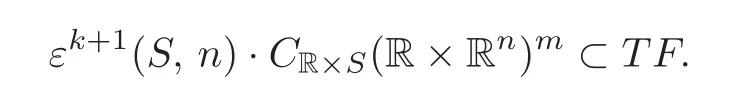
Then(2.1)holds.

Theorem 2.2Let f be a relative map-germ.If any relative map-germ g which has the same k-jet at S as f satisfies

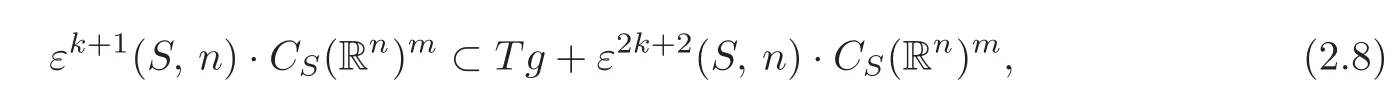
then f is weak k-AS,T-determined.

ProofLet?=2k+1.We denote byJ?the set of?-jets atSof elements ofEf,andG=A?S,T.LetV=π?1(jkf),whereπ:J?→Jkis the canonical projection.ThenGis a Lie group,andJ?is aC∞manifold with a vector space structure,soVis a subspace ofJ?.Therefore,Vis a connectedC∞manifold ofJ?.

First,we show thatVis in a single orbit of the action ofGonJ?.By Lemma 2.6,it suffces to show that

for allv∈V.Letπ?:Ef→J?be the canonical projection.From(2.8),we get

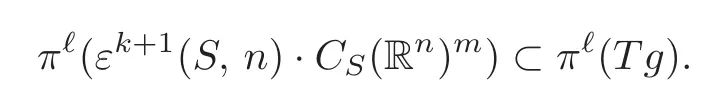
Note thatπ?(εk+1(S,n)·CS(Rn)m)=Tj?gVandπ?(Tg)=Tj?g(G·j?g),thus

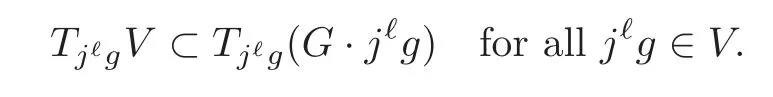
So(2.9)holds.Hencej?gandj?fare in the sameG-orbit.This means that there exists Φ∈AS,Tsuch thatj?Φ·j?g=j?f,that is,j?(Φ·g)=j?f.

Sincefalso satisfies(2.8),we get

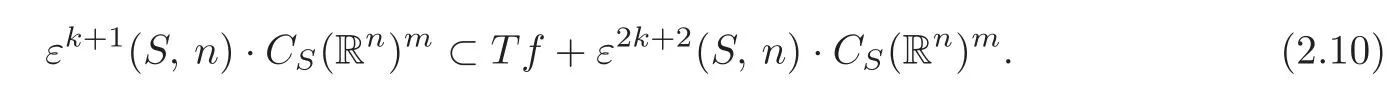
From the proof of Theorem 2.1,we have

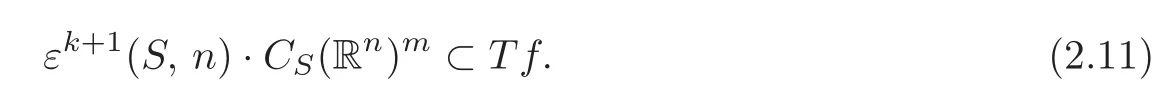
Thenfis weak(2k+1)-AS,T-determined.Noting thatj2k+1(Φ·g)=j2k+1f,it follows that Φ·gisAS,T-equivalent tof.Clearlygand Φ·gareAS,T-equivalent.Therefore,gandfareAS,T-equivalent.

Theorem 2.3Let f be a relative map-germ.If D is a CS(Rn)-module such that

(a)

(b)εk(S,n)·CS(Rn)m?ε(S,n)〈df〉+f?ε(T,m)·D+εk+1(S,n)·CS(Rn)m,then f is weak k-AS,T-determined.

ProofIt suffces to show that(a)and(b)imply the condition(2.8),for anyg∈Efwhich has the samek-jet atSasf.

By Lemma 2.1,we see that(a),(b)also hold withgreplacingf:

(a′)

(b′)εk(S,n)·CS(Rn)m?ε(S,n)〈dg〉+g?ε(T,m)·D+εk+1(S,n)·CS(Rn)m.

SetA=[ε(S,n)〈dg〉+g?ε(T,m)·D+εk(S,n)·CS(Rn)m]/[ε(S,n)〈dg〉+g?ε(T,m)·D+ε2k+2(S,n)·CS(Rn)m].It follows from(b′)that

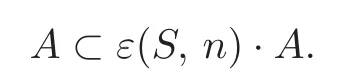
Besides,εk+2(S,n)·A=0.ThusA=0.So

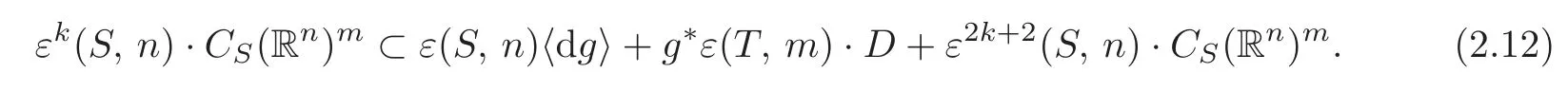
Combining(a′)and(2.12),we have

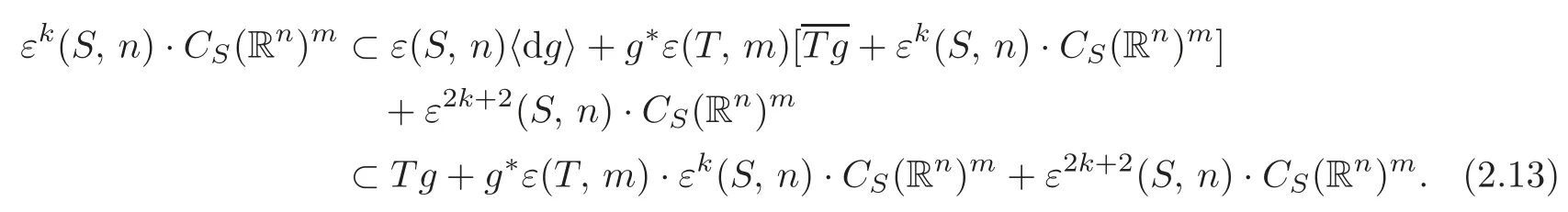
SetB=[Tg+εk(S,n)·CS(Rn)m)]/[Tg+ε2k+2(S,n)·CS(Rn)m].Then(2.13)implies

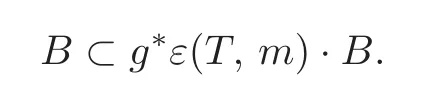
Note thatεk+2(S,n)·B=0,andg?ε(T,m)?ε(S,n).So

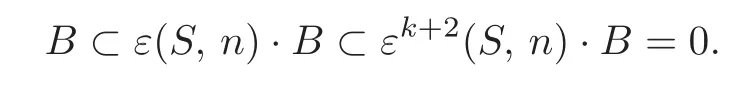
Therefore,B=0.It follows that

Applying Theorem 2.2,we complete the proof.

3 Weak Finite KS,T-Determinacy of Relative Map-Germs

For a map-germf,define

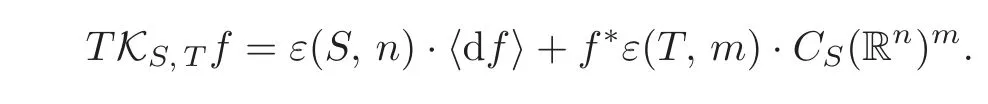
This is aCS(Rn)-submodule ofCS(Rn)m.

Theorem 3.1Let f be a relative map-germ.If

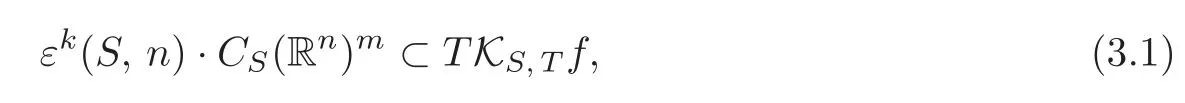
then f is weak k-KS,T-determined.

ProofLetgbe a relative map-germ which has the samek-jet atSasf.Define

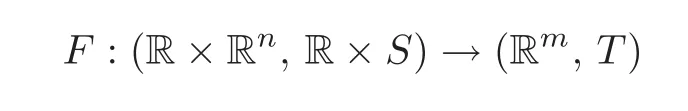
byF(λ,x)=f(x)+λh(x)andFλ(x)=F(λ,x),whereh=g?f.

For fixedλ0∈R,it is clear that we only have to prove thatFλisKS,T-equivalent toFλ0for anyλsuffciently close toλ0in R.

SinceFλ0?f=λ0h∈εk+1(S,n)·CS(Rn)m,from(3.1),it follows that

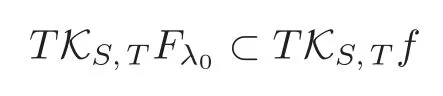
and

By Nakayama’s lemma,we get

HenceTKS,TFλ0also satisfies(3.1).Now we identifyCS(Rn)with the subring ofCR×S(R×Rn)composed of functions independent ofλ,soCS(Rn)?CR×S(R×Rn).From(3.1)–(3.2),we get

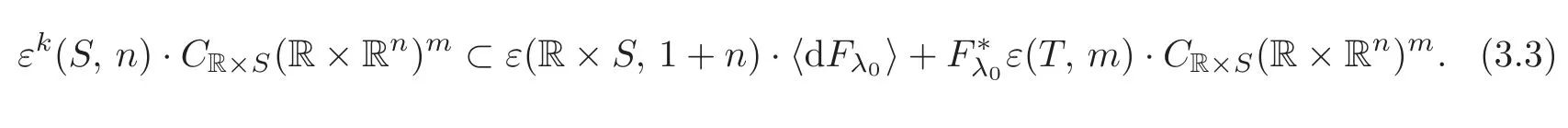
Also,sinceF?Fλ0=(λ ?λ0)h∈εk+1(S,n)·CR×S(R×Rn)m,by the same argument just as(3.2),we have

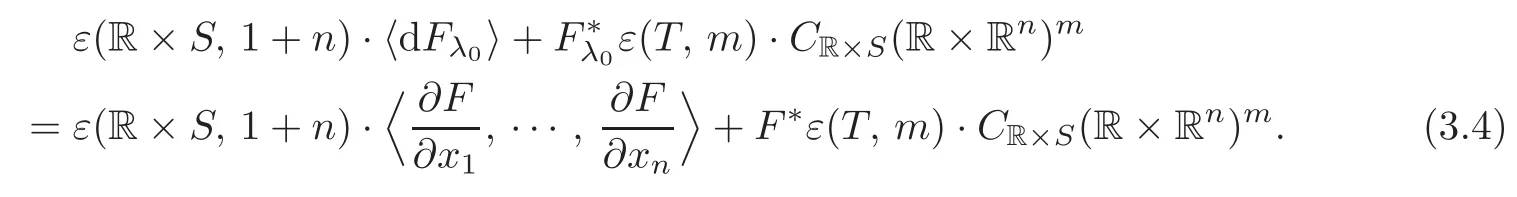
Combining(3.3)and(3.4),it shows that there exist germsXi∈ε(R×S,1+n),i=1,···,n,such that

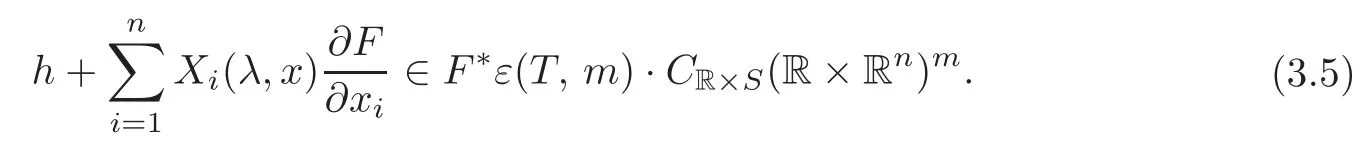
From(3.5),we can find a germ of the vector fieldXin R×Rnof the following form:

such thatDF(X)∈F?ε(T,m)·CR×S(R×Rn)m.By integrating the vector fieldX,we get a one-parameter family of diffeomorphismsφλ∈RS(n).So we can find am×mmatrixA(λ,x)with entries inCR×S(R×Rn)such that

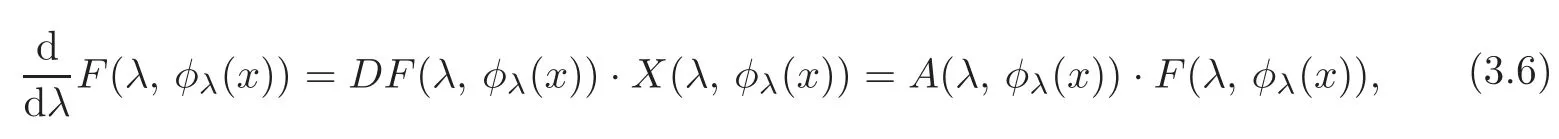
where matrixA(λ,x)has the form:

Hence,for fixedx∈Rn,F(λ,φλ(x))is a solution of the differential equation˙y=A(λ,φλ(x))ywith initial conditiony(λ0,x)=Fλ0(φλ0(x)).

Since the solution of this differential equation is unique and of the form:

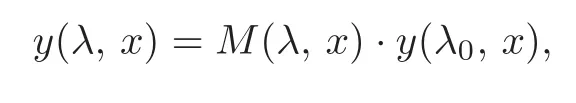
whereM(λ,x)is an invertible matrix,we can conclude that

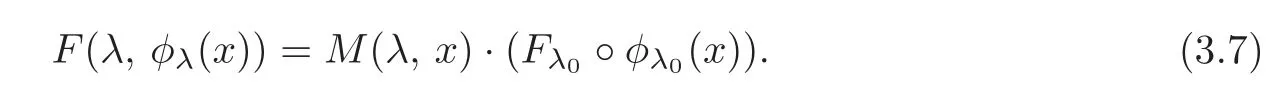
Therefore,f+λhandf+λ0hareKS,T-equivalent forλclose toλ0.By the connection of[0,1],we obtain thatfandgareKS,T-equivalent.

4 Application

Definition 4.1A relative map-germ f is AS,T-stable if all its unfoldings are trivial with respect to group AS,T.

Remark 4.1The argument given in[10]shows that a relative map-germfisAS,T-stable if and only if=CS(Rn)m.

Theorem 4.1Suppose that a relative map-germ f is AS,T-stable.Then f is weak(m+1)-AS,T-determined and weak(m+1)-KS,T-determined.

ProofSetA=CS(Rn)〈df〉+f?ε(T,m)·CS(Rn)m.This is aCS(Rn)-submodule ofCS(Rn)m.Consider the sequence of inclusion ofCS(Rn)-module:

Denote bycithe codimension ofinand letc0denote the codimension ofA+ε(S,n)CS(Rn)minCS(Rn)m.Thus the codimension ofinis equal to

Note thatf?(ε(T,m))·CS(Rn)m?A.By Remark 4.1,we have

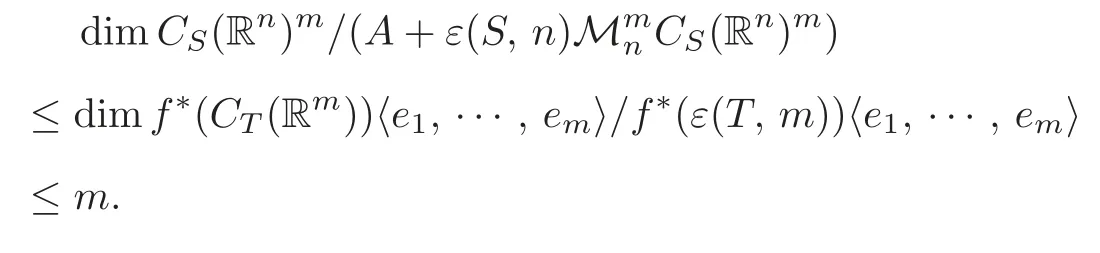
Therefore,by(4.1),c0+c1+···+cm≤m,thuscm=0.It follows that

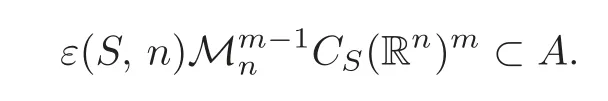
So,εm(S,n)CS(Rn)m?A.

Then it follows that

(a)εm(S,n)·CS(Rn)m?CS(Rn)〈df〉+f?ε(T,m)·CS(Rn)m.

Multiplying through(a)byε(S,n),we have

(b)εm+1(S,n)·CS(Rn)m?ε(S,n)〈df〉+f?ε(T,m)·ε(S,n)m.

On the other hand,by the definition ofAS,T-stable map-germ,we get

(c)ε(S,n)m=Tf?

Using Theorem 2.3 withD=ε(S,n)m,we can conclude thatfis(m+1)-AS,T-determined.

From(b),we get

(d)εm+1(S,n)·CS(Rn)m?TKS,Tf.

Thusfis weak(m+1)-KS,T-determined,by applying Theorem 3.1.

[1]Kong,L.L.and Pei,D.H.,Singularities of de Sitter Gauss map of timelike hypersurface in Minkowski 4-space,Sci.China Ser.A,51(2),2008,241–249.

[2]Pei,D.H.,Kong,L.L.and Sun,J.G.,et al.,Singularities of lightlike hypersurface in semi-Euclidean 4-space with index 2,Sci.China Ser.A,53(12),2010,3243–3254.

[3]Li,Y.C.and He,W.,Versal unfolding of equivariant bifurcation problems in more general case under two equivalent groups,Acta Math.Sci.,4,2008,915–923.

[4]Su,D.and Zhang,D.M.,The Newton filtration andd-determination of bifurcation problems related toC0-contact equivalence,Sci.China Ser.A,5,2006,660–668.

[5]Adachi,J.and Ishikawa,G.,Classification of phase singularities for complex scalar waves and their bifurcations,Nonlinearity,8,2007,1907–1925.

[6]Mather,J.N.,Stability ofC∞mappings III:Finitely determined map-germs,Publ.Math.I.H.E.S.,35,1969,127–156.

[7]Gaffney,T.and du Pless,A.A.,More on the determinacy of smooth map-germs,Invent.Math.,66,1982,137–163.

[8]Wall,C.T.C.,Finite determinacy of smooth map-germs,Bull.London Math.Soc.,13,1981,481–539.

[9]Porto,P.F.S.and Loibel,G.F.,Relative finite determinacy and relative stability of function-germs,Bol.Soc.Brasil Math.,9,1978,1–18.

[10]Radamila,B.,José A.G.and León K.,Relative versality for map-germ,Bolletino U.M.I.,7,1987,305–320.

[11]Kushner,L.and Leme,B.T.,Finite relative determinacy and relative stability,Pacif i c Journal of Math.,192(2),2000,315–327.

[12]Sun,B.H.and Wilson,L.C.,Determinacy of smooth germs with real isolated line singularities,Amer.Math.Soc.,127(9),2001,2789–2797.

[13]Grandjean,V.,Inf i nite relative determinacy of smooth function germs with transverse isolated singularity and relative Lojasiewicz conditions,J.London Math.Soc.,69(2),2004,518–530.

[14]Chen,L.,Sun,W.Z.and Pei,D.H.,Contact finite determinacy of relative map germs,Comm.Math.Res.,26(1),2010,1–6.

[15]Mather,J.N.,Stability ofC∞mappings IV:Classification of stable germs by R-algebras,Publ.Math.I.H.E.S.,37,1970,223–248.