Curvature Estimates for the Level Sets of Solutions to the Monge-Ampre Equation detD2u=1?
Chuanqiang CHEN Xinan MA Shujun SHI
1 Introduction
The Monge-Ampre equation is one of the most important fully nonlinear partial differential equations.It has the general form
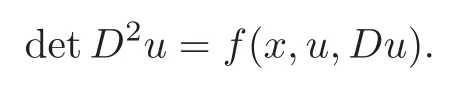
Here detD2udenotes the determinant of the Hessian matrixD2u,uis a function in the Euclicean space Rn,andfis a given function.It is elliptic when the Hessian matrixD2uis positive definite,namely,uis strictly convex.There is an extensive literature on the research of the Monge-Ampre equation(see[5,13]and the references therein).
In 2011,Hong,Huang,Wang[7]studied a class of degenerate elliptic Monge-Ampère equations in a smooth,bounded and strictly convex domain Ω of dimension 2.When they proved the existence of global smooth solutions to the homogeneous Dirichlet problem,they introduced the key auxiliary functionH,which is the product of curvatureκof the level line ofuand the cubic of|Du|,and got the uniformly lower bound ofHonThese imply an estimate for the lower bound of the curvature of the level line in some sense,which inspires us to study the following simplest homogeneous Dirichlet problem for the elliptic Monge-Ampère equation:

We find appropriatefunctions calledPfunctions,prove that thePfunctions attain their maxima on the boundary and get the upper bounded estimates for the Gauss curvature and the mean curvature of the level sets.
In order to state our results,we need the standard curvature formula of the level sets of a function(see[12]).Firstly,we recall the definition of elementary symmetric functions.For anyk=1,2,···,n,we set
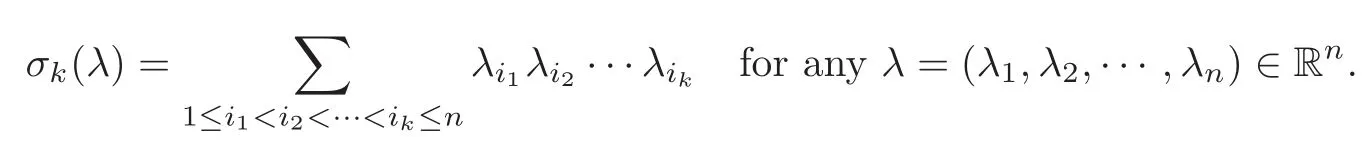
LetW=(wij)be a symmetricn×nmatrix,and we set
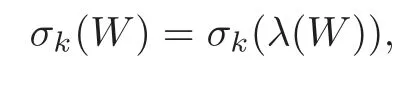
whereλ(W)=(λ1(W),···,λn(W))are the eigenvalues ofW.We also setσ0=1 andσk=0 for anyk>n.
Since the level sets of the strictly convex solution to the problems(1.1)are convex with respect to the normal direction?Du,we have the following formula on them-th curvature of the level sets of the solutionu,m=1,2,···,n?1,
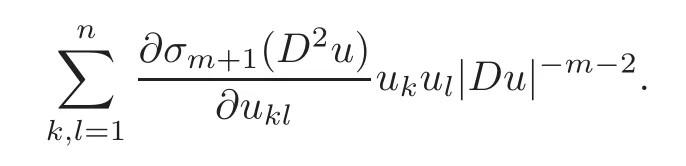
Whenm=1,
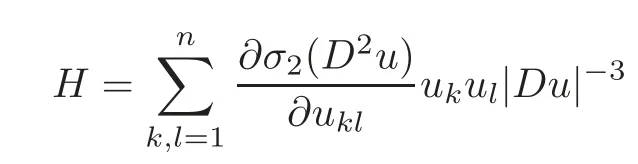
is the mean curvature of the level sets;Whenm=n?1,
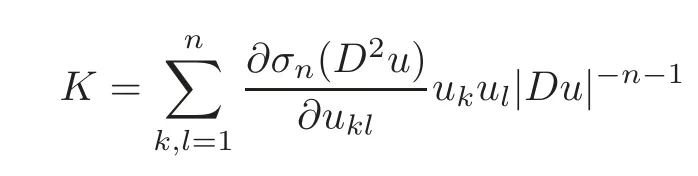
is the Gauss curvature of the level sets.
Theorem 1.1LetΩ?Rnbe a bounded convex domain,n≥2,and u be the strictly convex solution to(1.1).Then the function
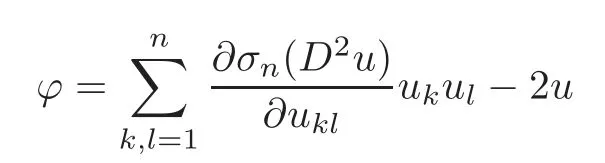
attains its maximum on the boundary?Ω.
Theorem 1.2Under the same assumptions as in the above theorem,we have that the function
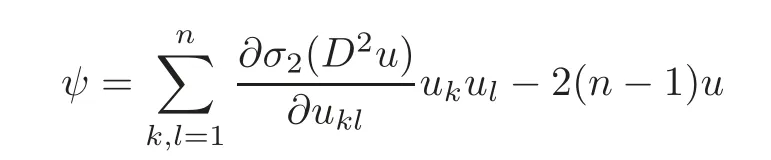
also attains its maximum on the boundary?Ω.Moreover,ψ attains its maximum inΩif and only ifΩis an ellipse for n=2or a ball for n≥3.
Naturally,we have the following corollary.
Corollary 1.1LetΩbe a smooth,bounded and strictly convex domain inRn,n≥2.If u is the solution to the problem(1.1),then the functions K|Du|n+1and H|Du|3attain their maxima only on the boundary?Ω.Thus,for x∈ΩΩ′,we have the following estimates:
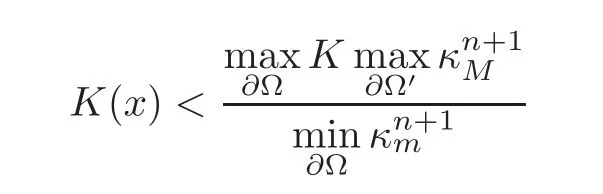
and
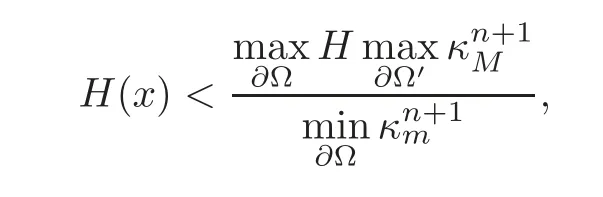
where
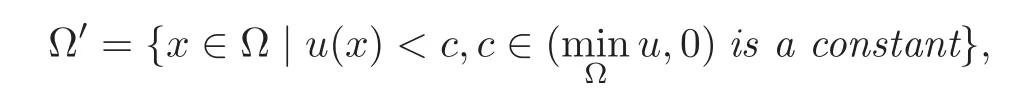
and κm,κMare the minimal and maximal principal curvatures of the level sets at a point respectively.
It should be mentioned that for the casen=2,Ma[10]and Anedda,Porru[1]considered the problem(1.1)and arrived at the conclusion of Theorem 1.1.Whenn=2,there is only one curvatureκfor the level sets at a point,soκ=K=Hand?=ψin Theorems 1.1–1.2.And
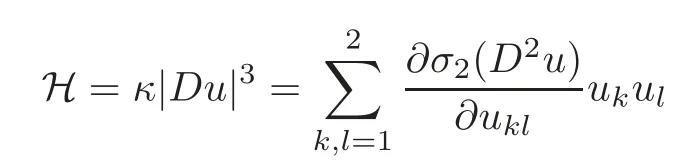
is the auxiliary function introduced by Hong,Huang and Wang[7].
There are also many papers that study curvature estimates for the level sets of solutions to partial differential equations(see[2–4,8–9,11]etc).
This paper is organized as follows.In Section 2,we prove Theorem 1.1 by establishing a differential inequality for the given function.In Section 3,through the same process as the proof of Theorem 1.1,we prove the first result in Theorem 1.2.Through the computation of the third derivatives for the solutionu,we prove the relation betweenψattaining its maximum in the interior and the shape of the domain Ω.Finally,we prove the corollary and give some remarks.
2 Proof of Theorem 1.1
LetD2u=(uij),(uij)=(uij)?1.Becauseuis the strictly convex solution to the equationσn(D2u)=detD2u=1,(uij)is positive definite andTherefore,
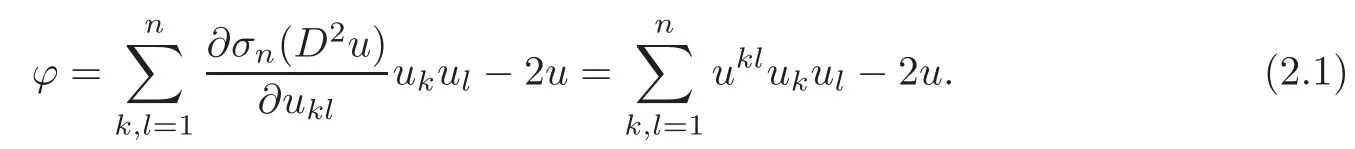
We will prove the following differential inequality:

From the differential inequality and by the maximum principle,?attains its maximum on the boundary?Ω.
In the following,we will prove(2.2).For anyxo∈Ω,we choose coordinates such that(uij(xo))is diagonal.All the following calculations are done atxo.
LetFrom direct computations,we have
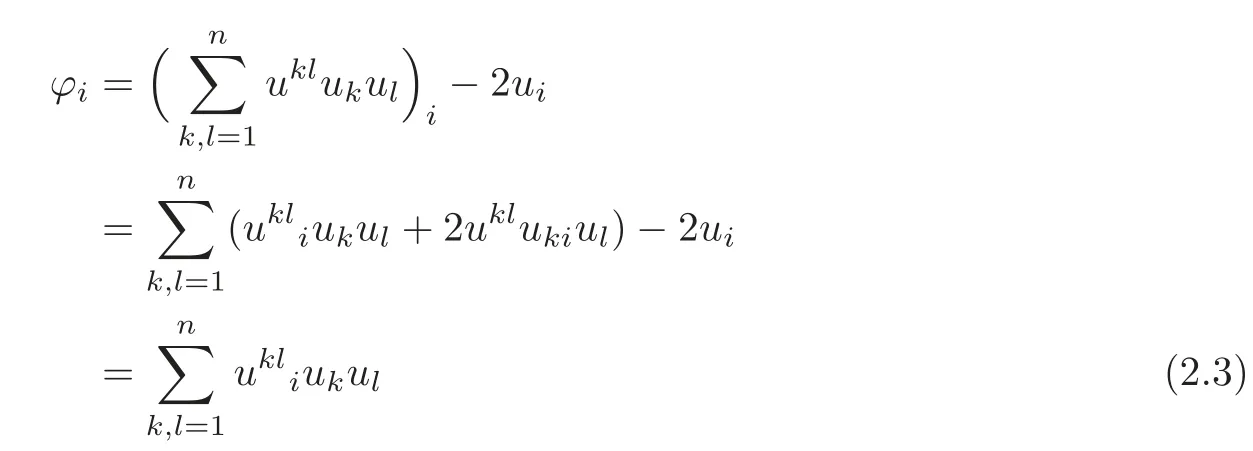
and
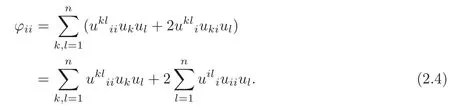
Thus
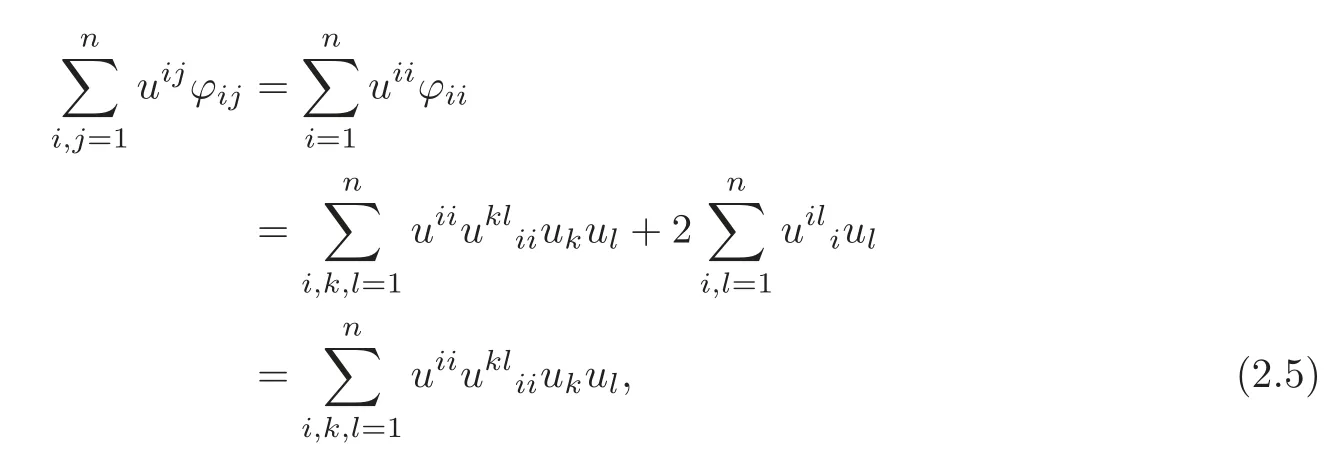
where we have usedin the last equality above.Since
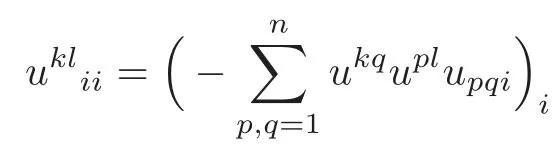
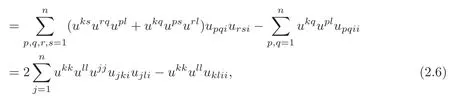
substituting(2.6)into(2.5),we obtain
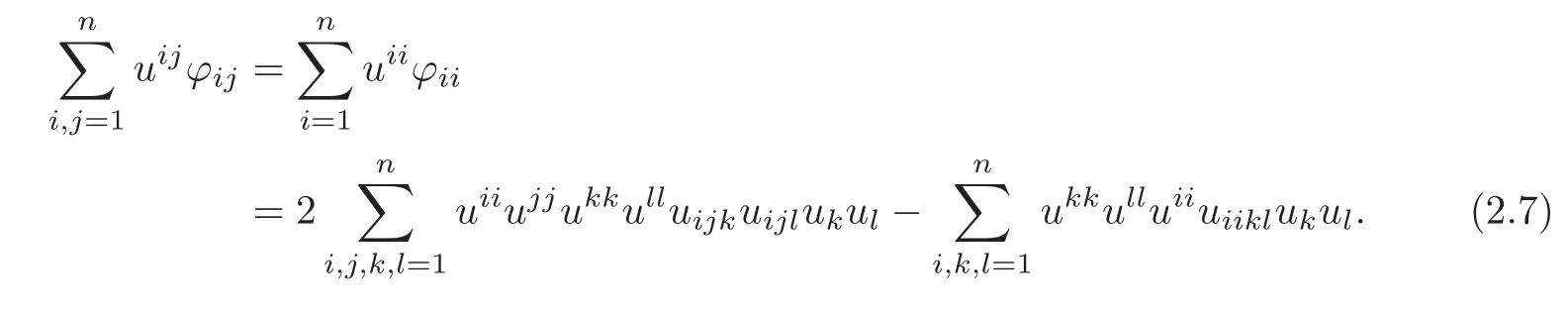
Because of the equation det(uij)=1,differentiating it once,we can get

i.e.,

Differentiating the equation once again,we have
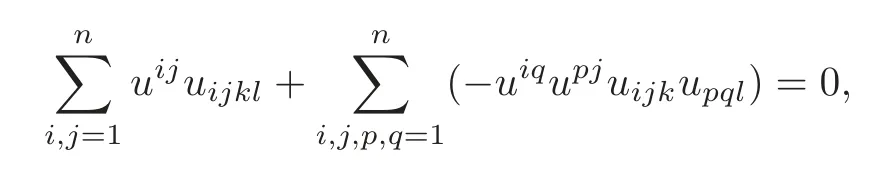
i.e.,

Substituting(2.9)into(2.7),we obtain
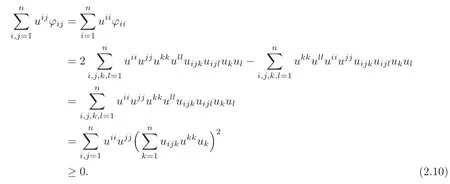
We have completed the proof of Theorem 1.1.
Remark 2.1Whenn=2,Ma[10]and Anedda,Porru[1]gave the result of Theorem 1.1 and further pointed out that?assumes its minimum on?Ω or at the unique critical pointx0ofu,i.e.,the point whereDu=0.We can also get the conclusion from the above proof directly.In fact,from(2.3),we get
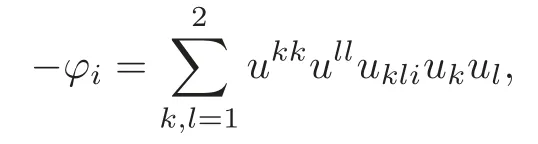
that is
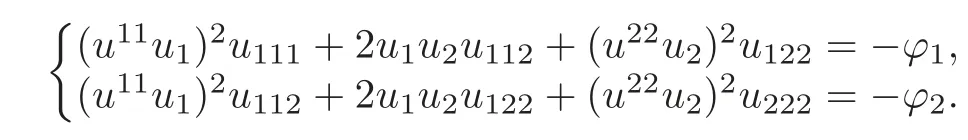
Here we have used the equation det(uij)=1.Combining with(2.8),that is
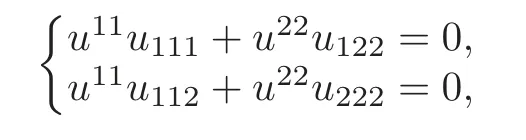
under the case of moduloD?,we obtain the homogeneous linear algebraic system about the third derivativesu111,u112,u122,u222ofu,
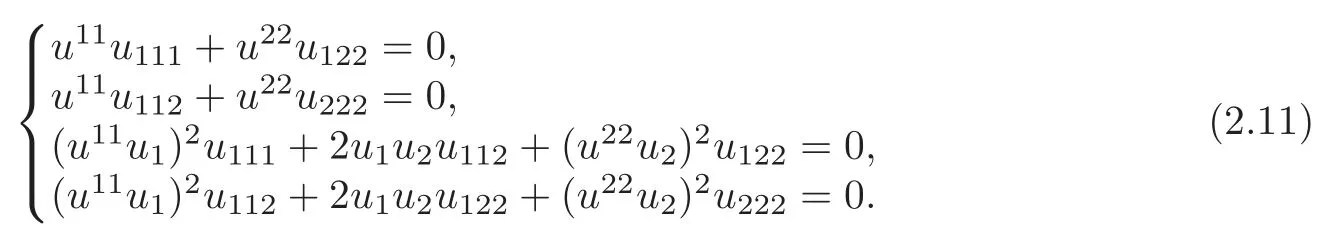
From direct computations,we get that the determinant of the coeffcient matrix iswhich is greater than 0 in Ω{x0}.Therefore
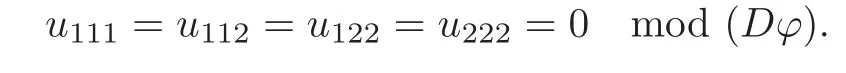
Consequently,from(2.10),we have that
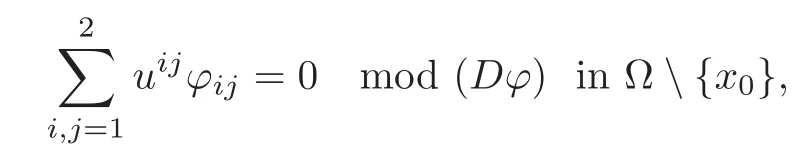
and by the maximum principle,?attains its minimum on?Ω or at the unique critical pointsx0.
3 Proof of Theorem 1.2
Let.Then
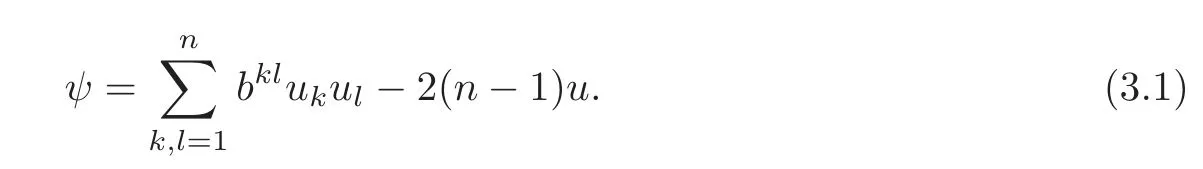
We will prove the following differential inequality:

From the differential inequality,and by the maximum principle,ψattains its maximum on the boundary?Ω.
In the following,we will prove the differential inequality(3.2).For anyxo∈Ω,we choose coordinates such thatD2u(xo)is diagonal.All the following calculations are done atxo.
LetFrom direct computations,we have
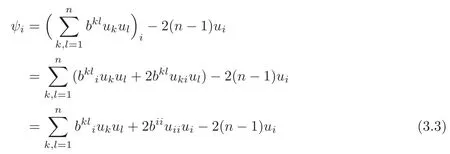
and
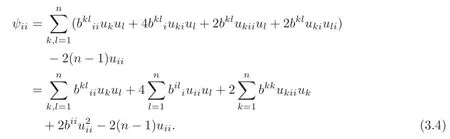
Therefore,
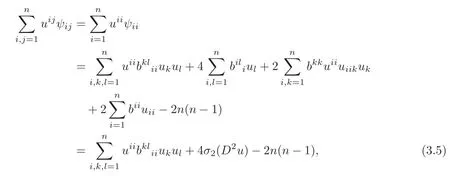
where we have used(2.8)and
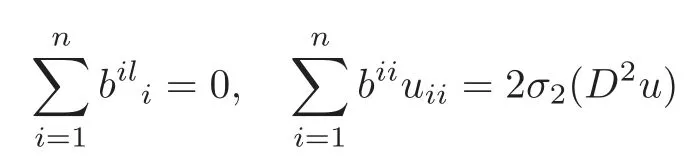
in the last equality above.Since
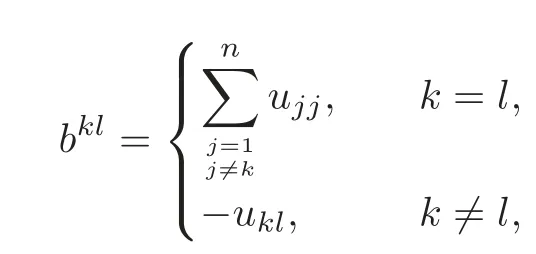
we have
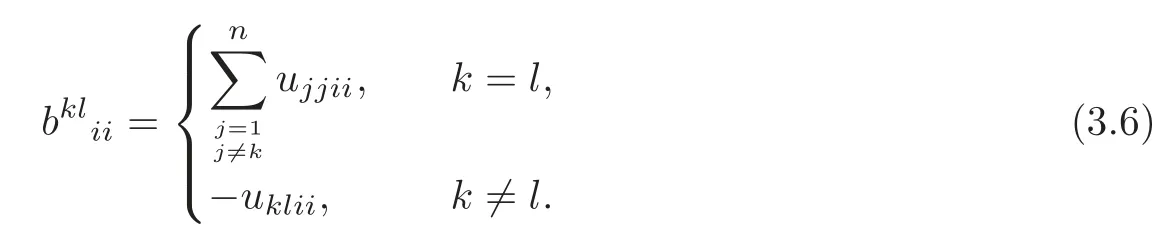
Substituting(3.6)into(3.5),we can get
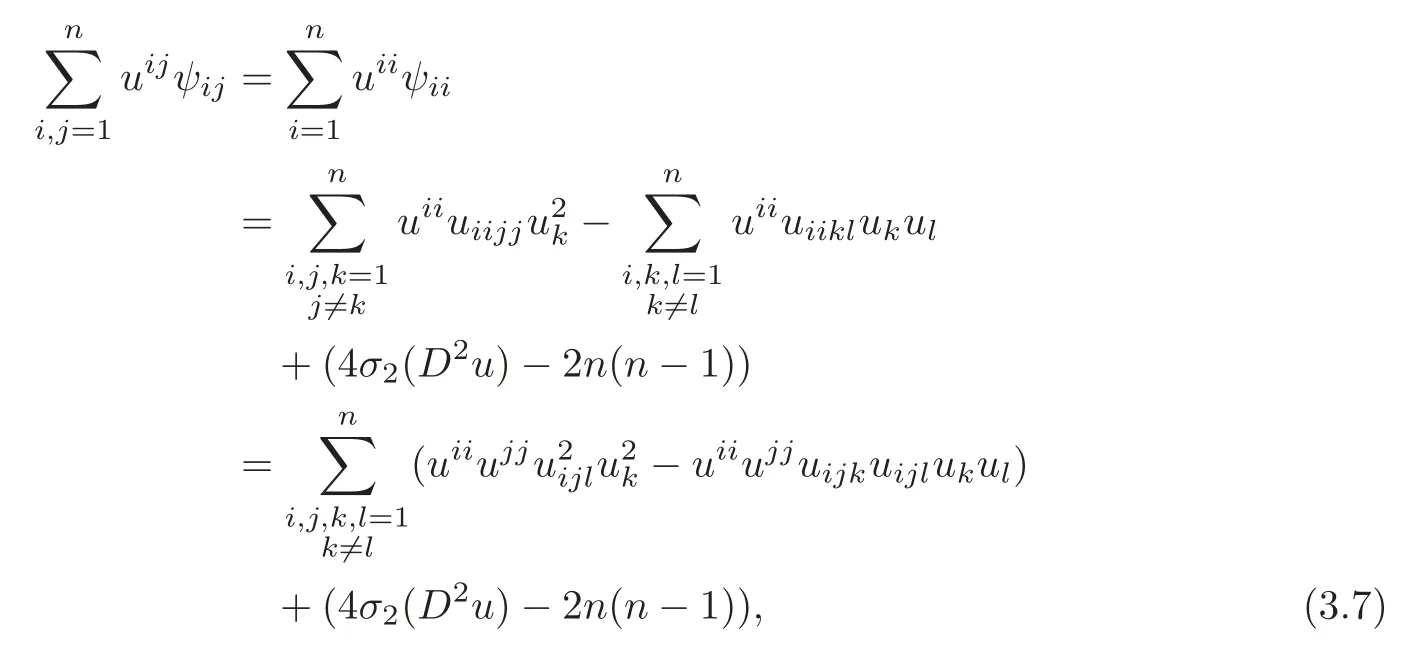
where we have used(2.9)in the last equality above.We also have
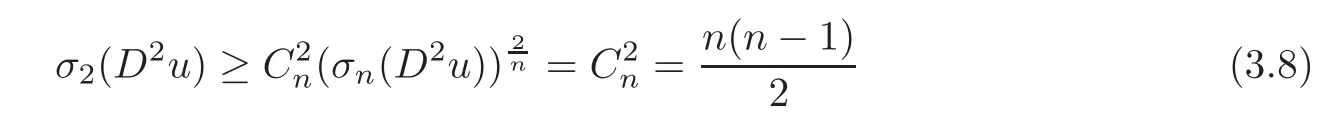
by Newton’s inequality(see[6,section 2.22]),and
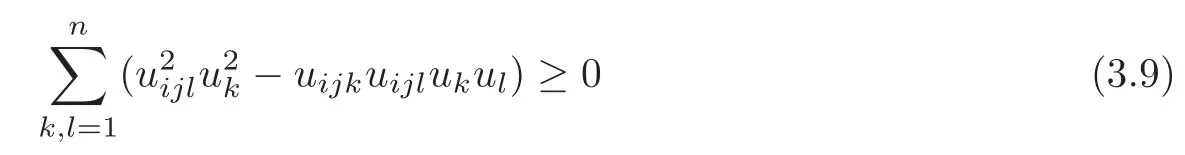
by Cauchy-Schwarz’s inequality.Combining(3.7)–(3.9),We can obtain that
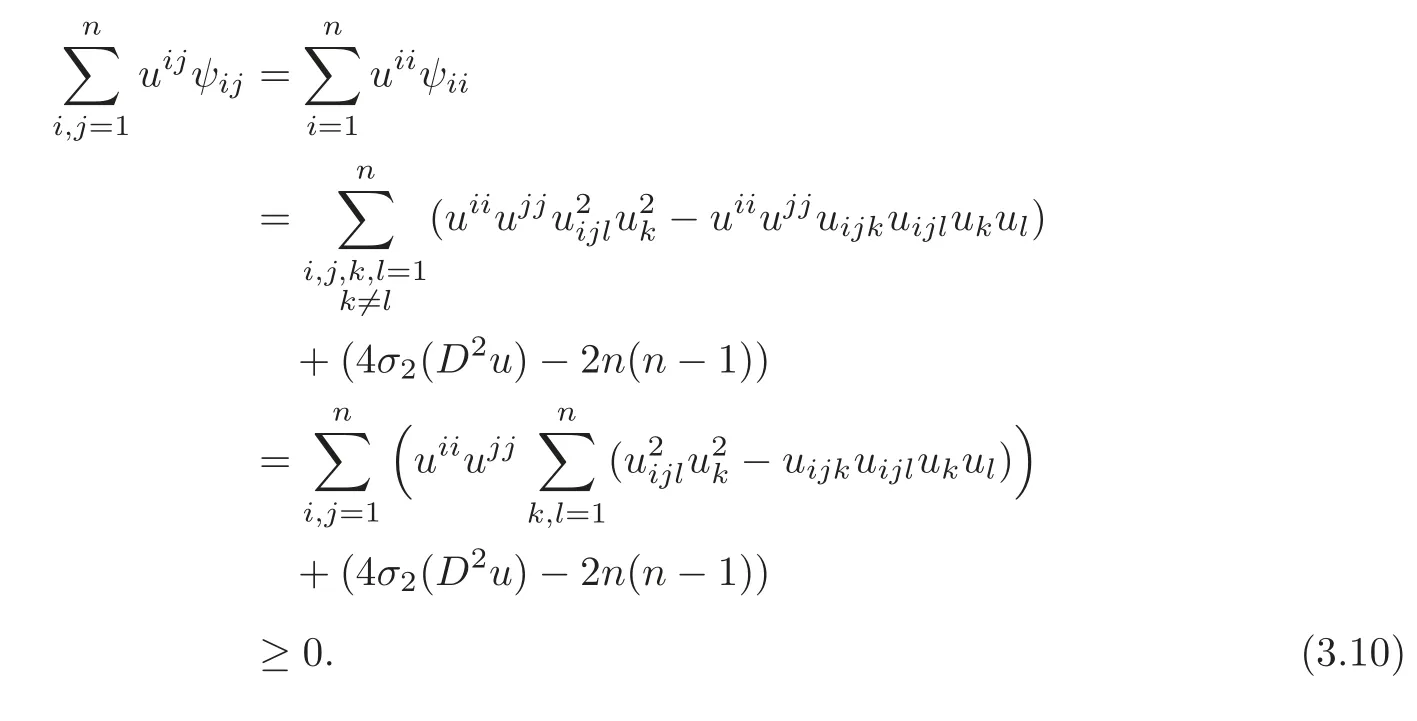
Furthermore,ψ=?whenn=2.It is easily obtained that ifψattains its maximum in Ω,then Ω is an ellipse by Remark 2.1 and vice versa.We also can get that Ω is an ellipse from(3.10).In fact,ifψattains its maximum in Ω,thenψis a constant in Ω.So(3.10)is the equality,that is,
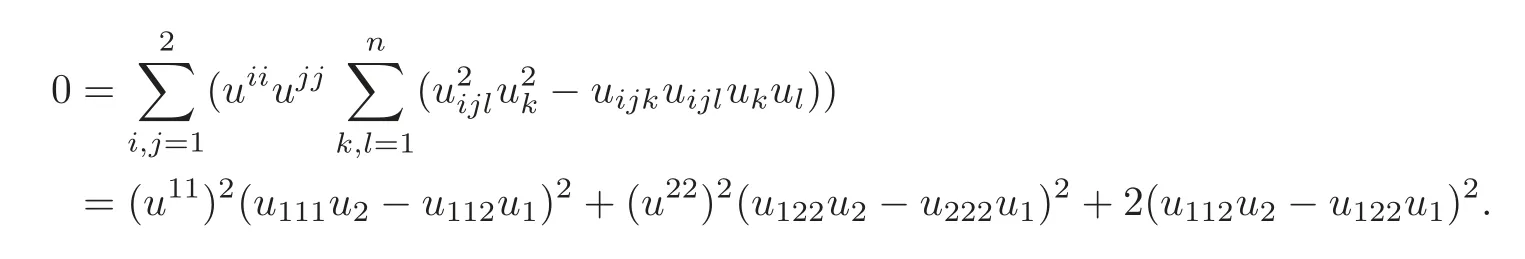
Becauseu11>0,andu22>0,

Sinceuis strictly convex,it has the unique critical pointx0,and(u1,u2)/=(0,0)in Ω{x0}.From the theory of linear algebraic systems,we have that the rank of the coeffcient matrix of the system(3.11)aboutu1,u2is less than 2,so
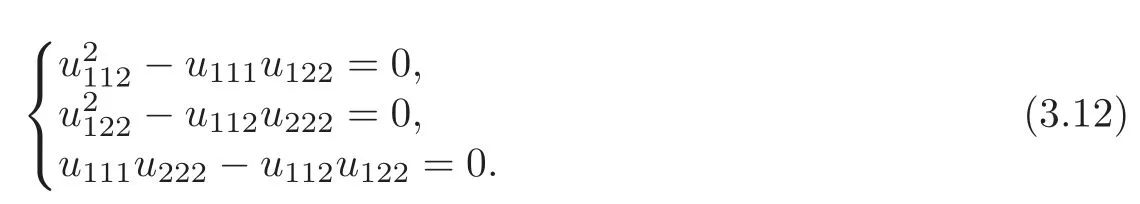
By(2.8),we get

Combining(3.12)with(3.13),we obtain
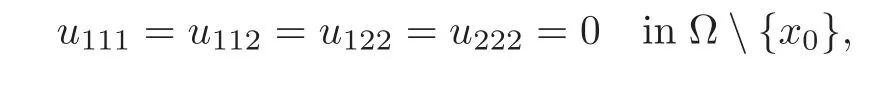
so all the third derivatives ofuvanish in Ω by the continuousness.Consequently,Ω ={u<0}must be an ellipse.
Whenn≥3,ifψattains its maximum in Ω,thenψis a constant in Ω.So(3.10)is the equality and we must have 4σ2(D2u)?2n(n?1)=0,that is,the equality holds in(3.8).But the equality holds in the Newton’s inequality,if and only if all the eigenvalues ofD2uare equal.Therefore,the eigenvalues ofD2uare equal to 1 by the equation detD2u=1 andD2uis the unit matrix.Consequently,
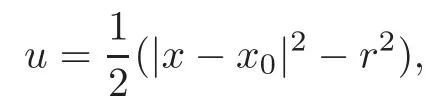
wherex0∈Rnis a fixed point,r>0 is a constant,and Ω={u<0}=Br(x0)is a ball.On the other hand,if Ω =Br(x0)is a ball,then the solution to the problem(1.1)isandψ≡(n?1)r2is a constant.
We have completed the proof of Theorem 1.2.
4 Proof of Corollary 1.1
We firstly give the boundary estimate of the gradientDufor the solution of(1.1).
Lemma 4.1LetΩbe a smooth,bounded and strictly convex domain inRn,x∈?Ωand κi(x),i=1,2,···,n?1be the principal curvatures of?Ωat x.Let
κm(x)=min{κi(x)|i=1,2,···,n?1},κM(x)=max{κi(x)|i=1,2,···,n?1}.
If u is the smooth and strictly convex solution of(1.1),then on the boundary?Ω,|Du|?Ωsatisfies the following estimate:
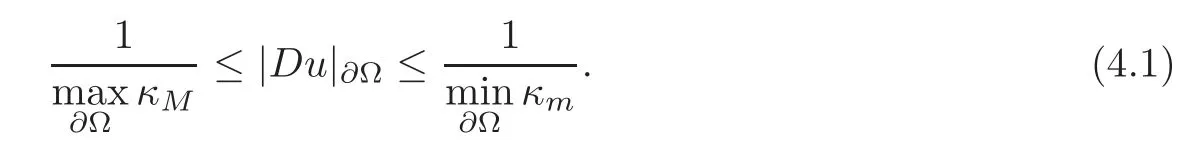
The same estimate is true forthat is,onthe boundary?Ω′,|Du|?Ω′satisfies
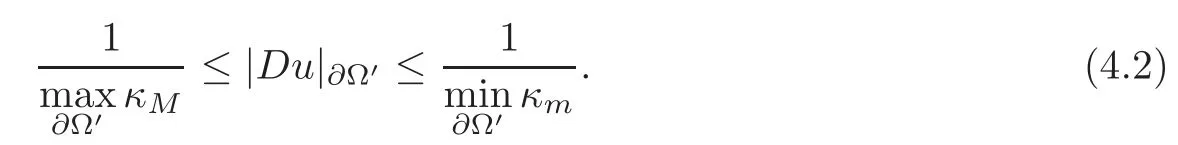
ProofFor any boundary pointx,let Ω?Ω0and Ω1?Ω be two balls of radiusandrespectively andx∈Ω∩Ωj,j=0,1.LetuΩj,j=0,1 be the solution to the problem
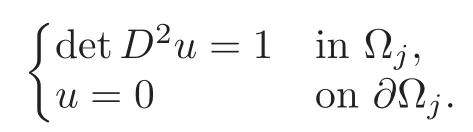
Sinceuvanishes on?Ω,it follows immediately that
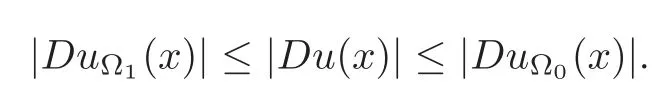
An explicit calculation yields
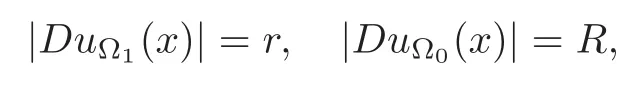
and thus
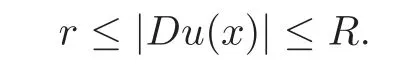
Therefore,
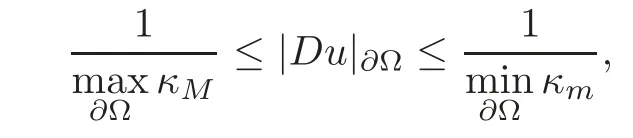
and(4.1)holds.For the same reasons,(4.2)also holds.
Next,we start the proof of Corollary 1.1.
Proof of Corollary 1.1By Theorem 1.1,we have thatK|Du|n+1?2utakes its maximum on the boundary?Ω.For anyx∈Ω,we have
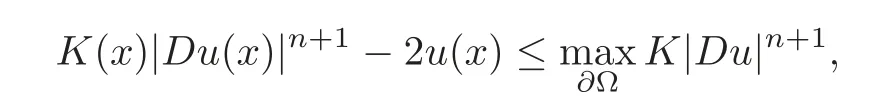
and thus,byu(x)<0,
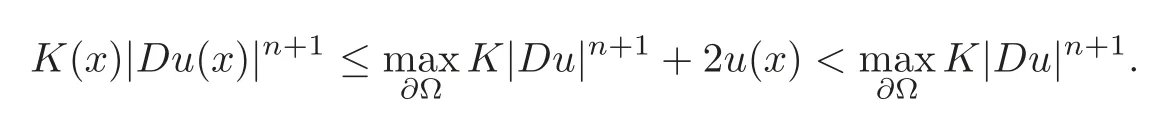
ThereforeK|Du|n+1attains its maximum only on the boundary?Ω.For the same reasons,by Theorem 1.2,we get thatH|Du|3also attains its maximum only on the boundary?Ω.Sinceuis strictly convex,|Du|increases along the increasing direction of the level sets.By Lemma 4.1,we have,forx∈ΩΩ′,
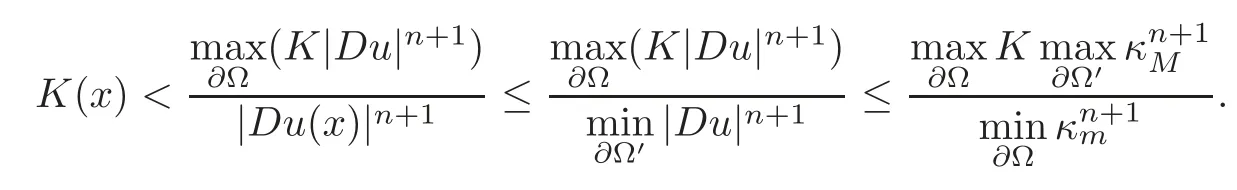
For the same reasons,
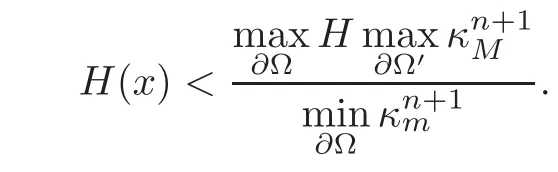
Remark 4.1Whenn=2,by Remark 2.1,?attains its minimum on?Ω or at the unique critical pointx0ofu.Therefore,we can furthermore give the positive lower bounded estimate for the curvature of the level lines.In fact,for anyx∈ΩΩ′,we have
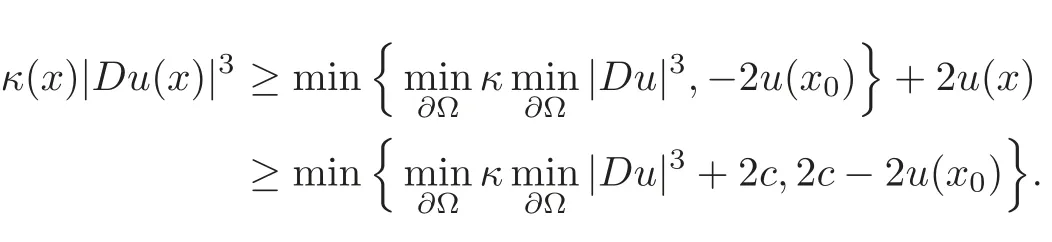
Since
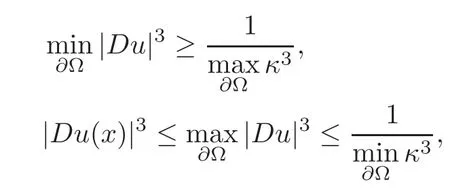
we obtain
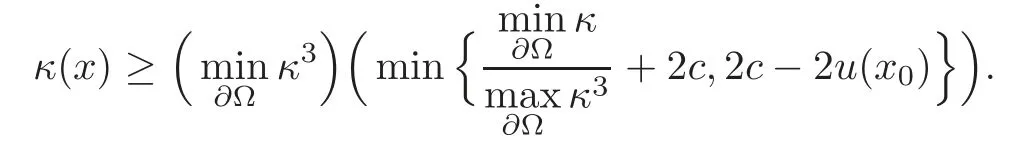
Remark 4.2It is more interesting to obtain the lower bounded estimate for the curvature of the level sets for Monge-Ampère equations in higher dimensions.If it is true,then it may be helpful to improve the regularity of solutions to degenerate elliptic Monge-Ampère equations in higher dimensions as in[7].
[1]Anedda,C.and Porru,G.,Problems on the Monge-Ampre equation in the plane,Contemporary Math.,400,2006,899–916.
[2]Chang,S.Y.A.,Ma,X.N.and Yang,P.,Principal curvature estimates for the convex level sets of semilinear elliptic equations,Discrete Contin.Dyn.Syst.,28(3),2010,1151–1164.
[3]Chen,C.and Shi,S.,Curvature estimates for the level sets of spatial quasiconcave solutions to a class of parabolic equations,Sci.China Math.,54(10),2011,2063–2080.
[4]Guan,P.and Xu,L.,Convexity estimates for level sets of quasiconcave solutions to fully nonlinear elliptic equations,J.Reine Angew.Math.,680,2013,41–67.
[5]Gutiérrez,C.E.,The Monge-Ampre equation,Progress in Nonlinear Differential Equation and Their Applications,Vol.44,Birkh¨aser,Boston,2001.
[6]Hardy,G.H.,Littlewood,J.E.and Pólya,G.,Inequalities,Cambridge University Press,Cambridge,1988.
[7]Hong,J.,Huang,G.and Wang,W.,Existence of global smooth solutions to Dirichlet problem for degenerate elliptic Monge-Ampère equations,Comm.Part.Diff.Eq.,36,2011,635–656.
[8]Jost,J.,Ma,X.N.and Ou,Q.,Curvature estimates in dimensions 2 and 3 for the level sets ofp-harmonic functions in convex rings,Trans.Amer.Math.Soc.,364,2012,4605–4627.
[9]Longinetti,M.,Convexity of the level lines of harmonic functions,Boll.Un.Mat.Ital.A,6,1983,71–75.
[10]Ma,X.N.,Some estimates for Monge-Ampre equations in two dimensions,preprint,1998.
[11]Ma,X.N.,Ou,Q.and Zhang,W.,Gaussian curvature estimates for the convex level sets ofp-harmonic functions,Comm.Pure Appl.Math.,63,2010,935–971.
[12]Trudinger,N.S.,On new isoperimetric inequalities and symmetrization,J.Reine Angew.Math.,488,1997,203–220.
[13]Trudinger,N.S.and Wang,X.J.,The Monge-Ampre equation and its geometric application,Handbook of Geometric Analysis,Vol.I,467–524,Adv.Lect.Math.,Vol.7,Higher Euducation Press,Beijing,2008.
 Chinese Annals of Mathematics,Series B2014年6期
Chinese Annals of Mathematics,Series B2014年6期
- Chinese Annals of Mathematics,Series B的其它文章
- Weak Finite Determinacy of Relative Map-Germs?
- Schur Convexity for Two Classes of Symmetric Functions and Their Applications?
- Evolution Equations of Curvature Tensors Along the Hyperbolic Geometric Flow
- The Brio System with Initial Conditions Involving Dirac Masses:A Result Afforded by a Distributional Product?
- On the Rayleigh-Taylor Instability for Two Uniform Viscous Incompressible Flows?
- Symplectic Group Actions on Homotopy Elliptic Surfaces?
