Mingbao SUN Nanbo CHEN Songhua LI Yinghui ZHANG

1 Introduction

We use the following notations throughout this paper:Let Rndenote then-dimensional Euclidean space over the field of real numbers(n≥2),0,i=1,2,···,n},={x=(x1,x2,···,xn)∈Rn:xi＜0,i=1,2,···,n},R=(?∞,+∞)andN={1,2,···,n,···}.Forx=(x1,x2,···,xn)∈Rn,y=(y1,y2,···,yn)∈Rnandα∈R,we denote by

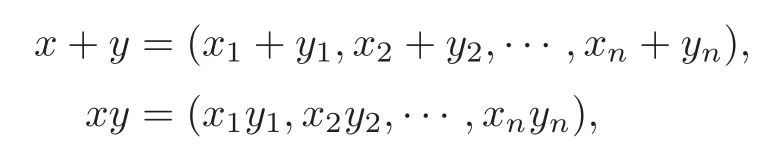
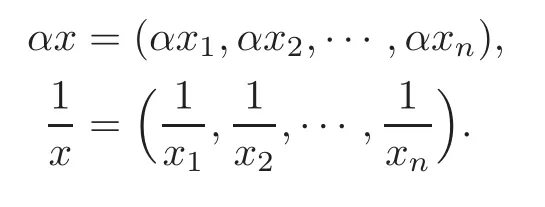
Schur in[1]gave the definition of the Schur convex function as in Definition 1.1,which can be found in[2].

Definition 1.1LetΩ?Rnbe a set,a real-valued function f onΩis said to be Schur convex if

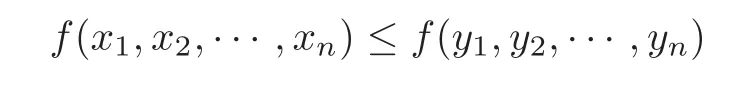
for each pair of n-tuples x=(x1,x2,···,xn)and y=(y1,y2,···,yn)inΩ,such that x?y,that is

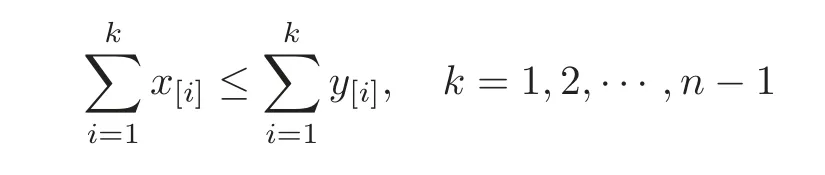
and

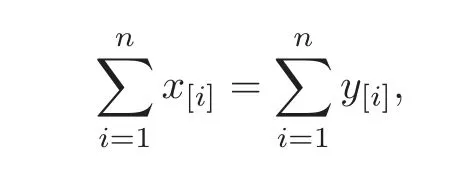
where x[i]denotes the i-th largest component of x.f is called Schur concave if?f is Schur convex.

The above Schur convexity has many important applications in analytic inequalities(see[3–13]),linear regression(see[14]),combinatorial optimization(see[15]),graphs and matrices(see[16]),gamma and digamma functions(see[17]),reliability and availability(see[18])and other related fields.Hardy,Littlewood,and Polya were also interested in some inequalities that are related to the Schur convex functions(see[19]).

Recently,Schur convexity of the some symmetric functions and their applications have been investigated by many authors,see for instance(see[3,20–24])and the references therein.

In[3],Guan defined the following symmetric functions:

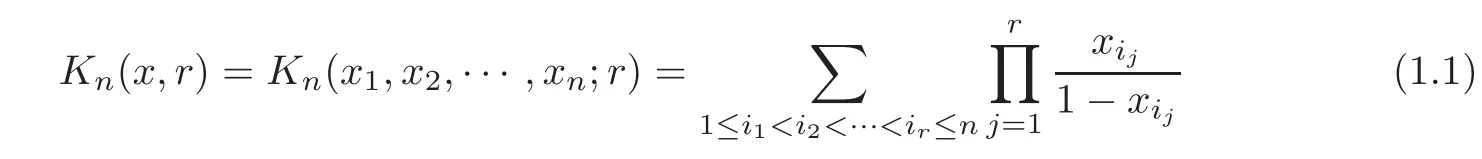
forx=(x1,···,xn)∈[0,1)n={x=(x1,x2,···,xn)∈Rn:0≤xi＜1,i=1,2,···,n},r∈Nandr≤n,wherei1,i2,···,inare positive integers.The Schur convexity and Schur geometric convexity forKn(x,r)were discussed and some inequalities were established by use of the theory of majorization in[3].

In[20],Chu et al.had a further discussion on the Schur comvexity ofKn(x,r),in particular,solved an open problem proposed by Guan in[3].

Xia and Chu in[21–22]defined the symmetric functionsMn(x,r)andNn(x,r)as follows:

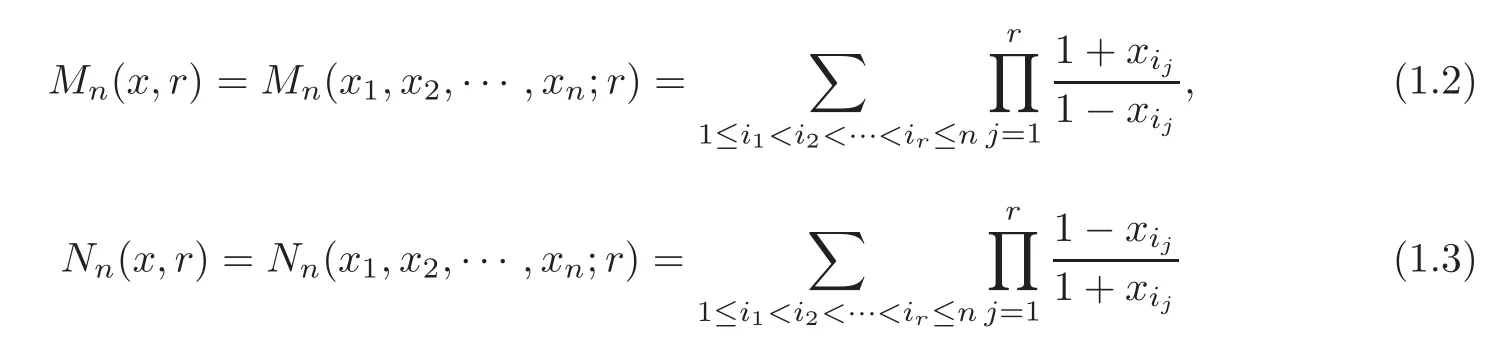
forx=(x1,···,xn)∈(0,1)n,r∈Nandr≤n,wherei1,i2,···,inare positive integers.Xia et al.[23]defined the symmetric function

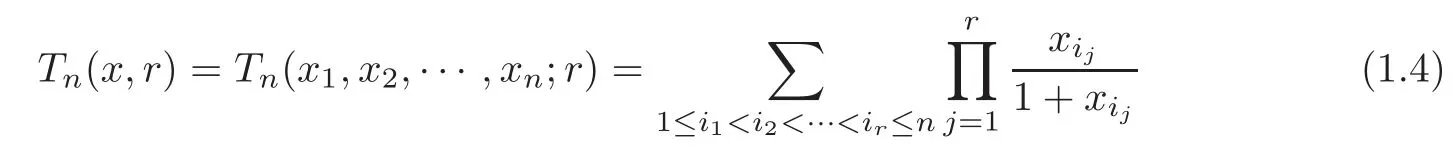
forx=(x1,···,xn)∈,r∈Nandr≤n,wherei1,i2,···,inare positive integers.In[21–23],they discussed the Schur convexity,Schur multiplicative convexity and Schur harmonic convexity forMn(x,r),Nn(x,r)andTn(x,r),respectively,and established some inequalities.

In this paper,motivated by ideas in[3,20–23],we define the following symmetric functions:

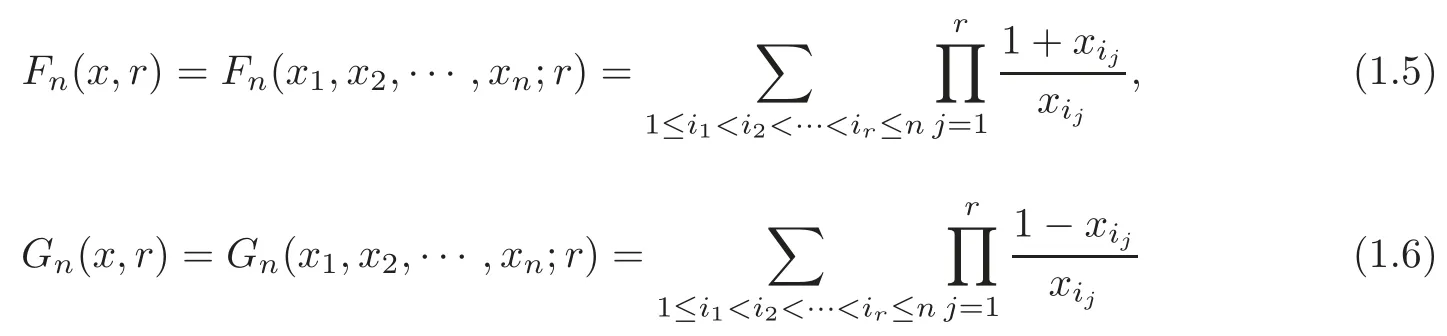
forx=(x1,···,xn)∈∪,r∈Nandr≤n,wherei1,i2,···,inare positive integers.The main purpose of this paper is to discuss the Schur convexity for the symmetric functionFn(x,r),As applications,by a bijective transformation of independent variable for a Schur convex function,we obtain the Schur convexity ofGn(x,r)and the Schur convexity for the symmetric functionsMn(x,r),Nn(x,r)andTn(x,r),which subsumes the main results in[3,20–23];establish some inequalities by use of the theory of majorization.In particular,we derive from our results the Weierstrass inequalities(see[25,P.260])and the Ky Fan’s inequality(see[26]),and give a generalization of Safta’s conjecture(see[27–28])in then-dimensional space and others.

This paper,except for the introduction,is divided into three sections.In Section 2,we introduce and establish some lemmas.By using the results of Section 2,we will give the main results in Section 3.Finally,some applications are given by use of the theory of majorization.

2 Some Lemmas

In this section,we introduce and establish some lemmas,which will be used in the proof of our main results.

Lemma 2.1LetΩ?Rnbe a symmetric convex set with nonempty interiorintΩ,and f:Ω→R be a Schur convex(or concave,respectively)function onΩ.If the transformation T:Ω′→Ωdefined by x=ay+b(a/=0)for y∈Ω′,a,b∈R is bijective,put ?(y)=f(ay+b)=f(x),then ?:Ω′→R is a Schur convex(or concave,respectively)function onΩ′.HereΩis a symmetric set which means that x∈Ωimplies Px∈Ωfor any n×n permutation matrix P.

ProofWe give only the proof in the case of?being Schur convex on Ω′,since the proof in the others case is similar.

It is easy to derive that Ω′is a symmetric convex set with nonempty interior.For anyy′,y′′∈Ω′,y′?y′′,sinceTis bijective,there exist only pointx′,x′′∈Ω such thatx′=ay′+b,x′′=ay′′+bandx′=ay′+b?ay′′+b=x′′.Noting thatfis Schur convex on Ω.

We havef(x′)≤f(x′′).Further we obtain

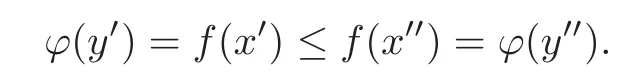
Therefore,?is Schur convex on Ω′.

Lemma 2.2(see[29])LetΩ?Rnbe a symmetric convex set with nonempty interiorintΩ,and f:Ω→R be a continuous symmetry function onΩ.If f is differentiable onintΩ,then f is Schur convex onΩif and only if

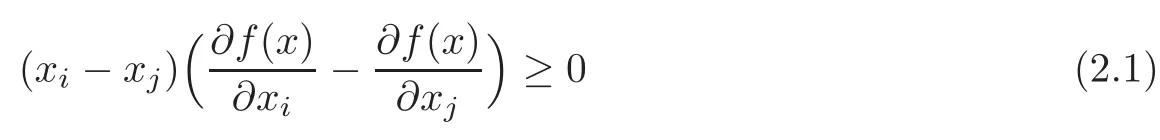
for i,j=1,2,···,n and all x=(x1,···,xn)∈intΩ.And f is Schur concave onΩif and only if the inequality(2.1)is reversed.Here f is a symmetric function inΩwhich means that f(Px)=f(x)for any x∈Ωand any n×n permutation matrix P.

Remark 2.1Sincefis symmetric,the Schur’s condition in Lemma 2.2,i.e.(2.1)can be reduced as

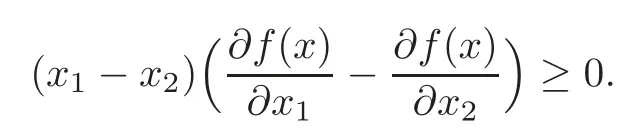
Fort=(t1,t2,···,tn)∈(n≥2)andr∈{1,2,···,n},ther-th order elementary symmetric functionEn(t,r)(see[30])is defined as

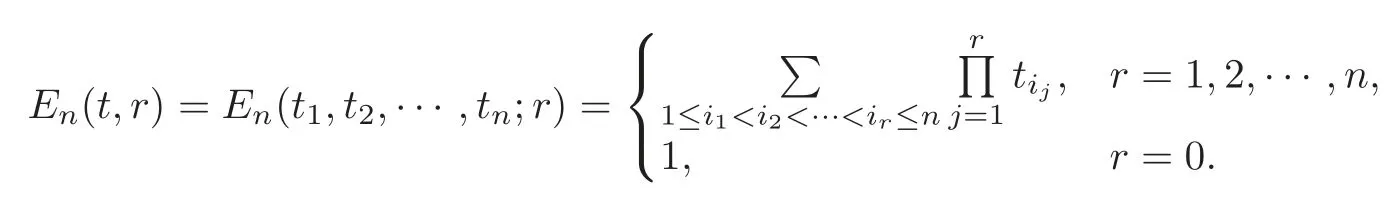
wherei1,i2,···,inare positive integers.

Lemma 2.3Let t=(t1,t2,···,tn)If1≤r≤n?1,then

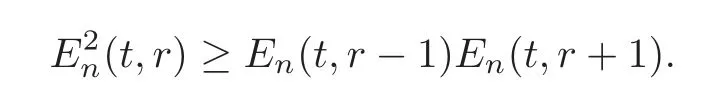
ProofFort=(t1,t2,···,tn)∈,the proof of Lemma 2.3 can be found in[20,31].Applying the known results fort=(t1,t2,···,tn)∈,we derive that Lemma 2.3 is valid fort=(t1,t2,···,tn)∈.

Lemma 2.4Let n≥3,1≤r≤n?1.Then the function

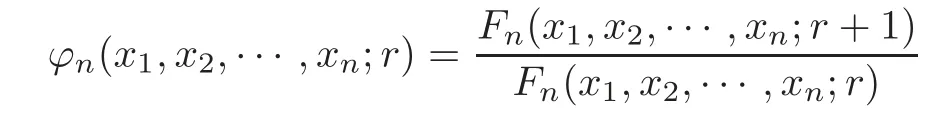
is decreasing with respect to xi(i=1,2,···,n)on(?1,0).

ProofSince?n(x1,x2,···,xn;r)is symmetric with respect to(x1,x2,···,xn)∈(?1,0)n,we give only the proof in the case of?n(x1,x2,···,xn;r)being decreasing with respect tox1on(?1,0).The proof is divided into three cases.

Case 1 Ifr=1,then

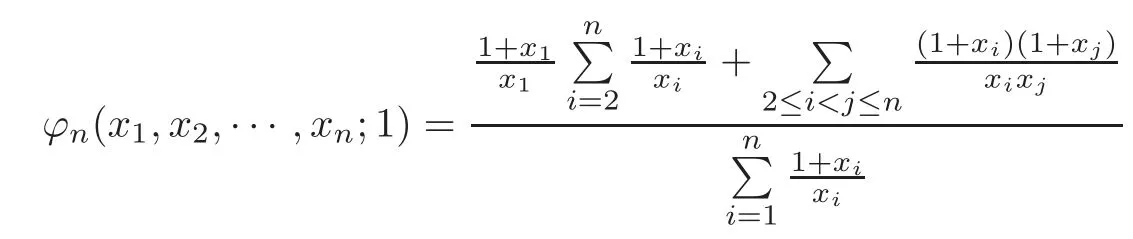
and

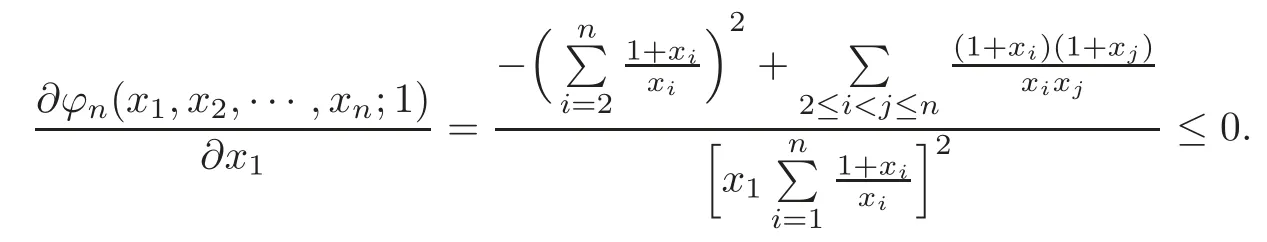
Case 2 Ifr=n?1,then

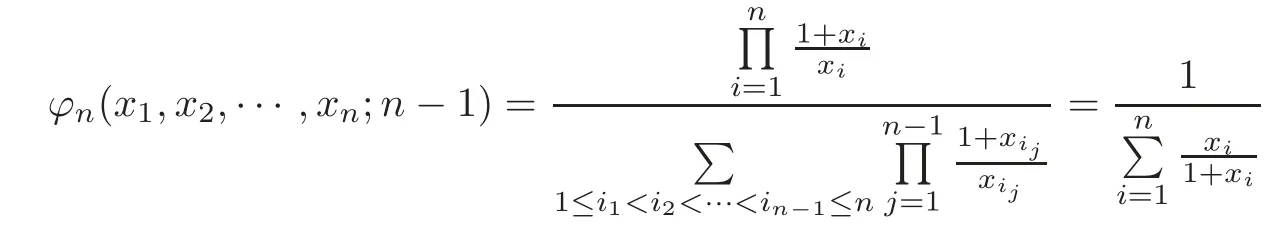
and

Case 3 Ifn≥4 and 2≤r≤n?2,then

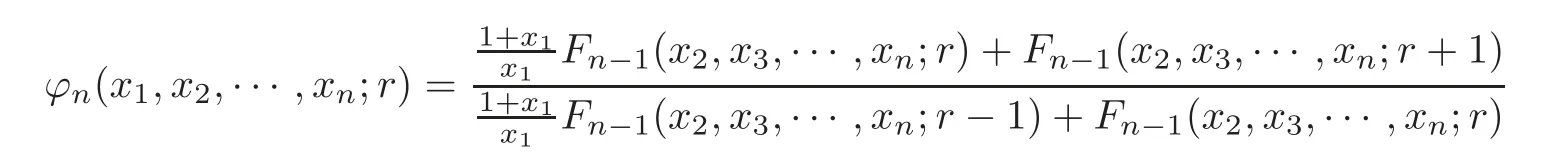
and

where Δ =(1+x1)Fn?1(x2,x3,···,xn;r?1)+x1Fn?1(x2,x3,···,xn;r),ti=i=1,2,···,n?1.From Lemma 2.3 and(2.2),we have

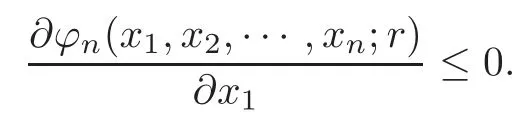
This completes the proof of Lemma 2.4.

Lemma 2.5(see[10])Let x=(x1,x2,···,xn)∈then

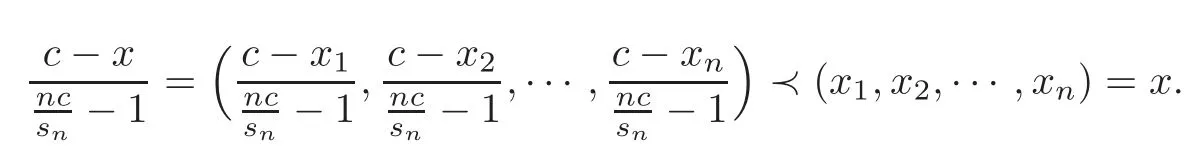
From Lemma 2.5,we have the following lemma.

Lemma 2.6Let x=(x1,x2,···,xn)∈then

Lemma 2.7(see[10])Let x=(x1,x2,···,xn)∈then

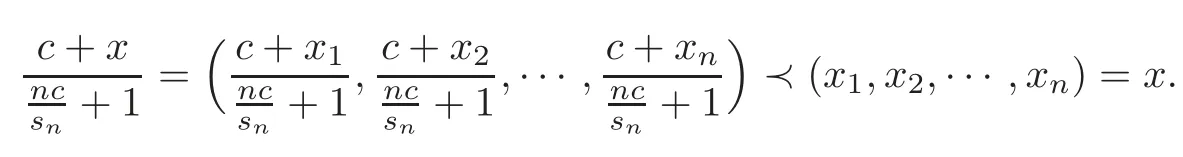
From Lemma 2.7,we derive the following lemma.

Lemma 2.8Let x=(x1,x2,···,xn)∈,and

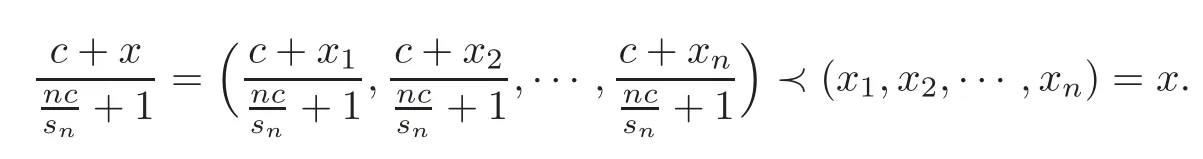
Lemma 2.9(see[32])Let x=(x1,x2,···,xn)∈Rn,andthen

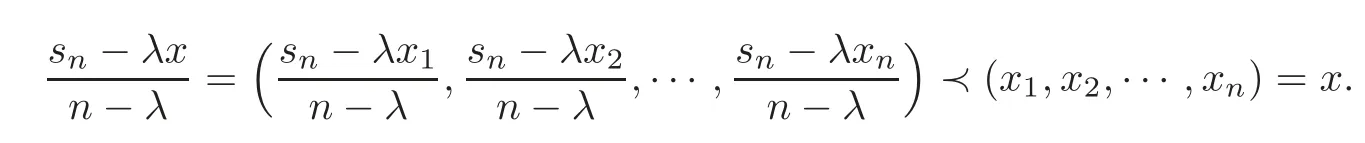
3 Main Results

Theorem 3.1For n≥2,the function Fn(x,1)is Schur concave in,and Schur convex in.

ProofFrom(1.5),we have

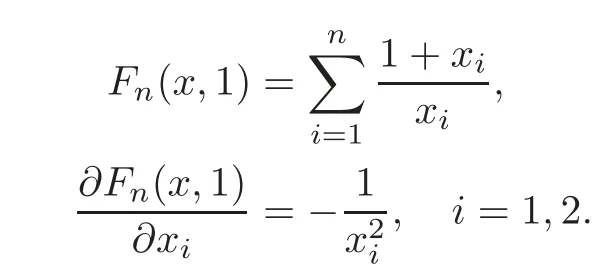
Whenx=(x1,x2,···,xn)∈,we derive

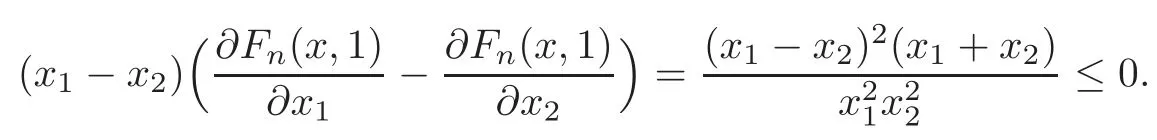
Applying Lemma 2.2 and Remark 2.1,we obtain thatFn(x,1)is Schur concave in.Similarly,it is easy to see thatFn(x,1)is Schur convex in.

Theorem 3.2For n≥2and2≤r≤n,

(1)if r is an even integer(or odd integer,respectively),then Fn(x,r)is Schur convex(orconcave,respectively)in

(2)if r is an even integer(or odd integer,respectively),then Fn(x,r)is Schur concave(orconvex,respectively)in

(3)Fn(x,r)is Schur concave in(?∞,?1]n,and Schur convex in.

ProofHere we give only the proof in the case ofrbeing an even integer,since the proof in the case ofrbeing an odd integer is similar.

(1)According to Lemma 2.2 and Remark 2.1,we only need to prove that

forx=(x1,x2,···,xn)

To prove(3.1),we divide the proof into five cases.

Case 1 Ifn≥2,r=n,then from(1.5),we have

By(3.2),we obtain

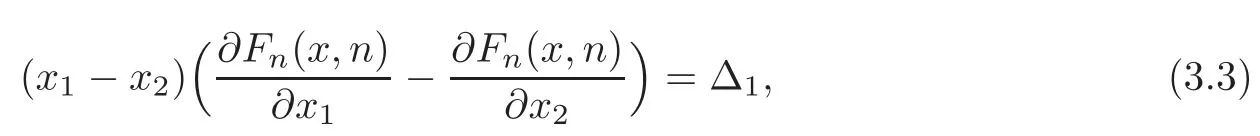
Case 2 Ifn=3,r=2,then(1.5)yields

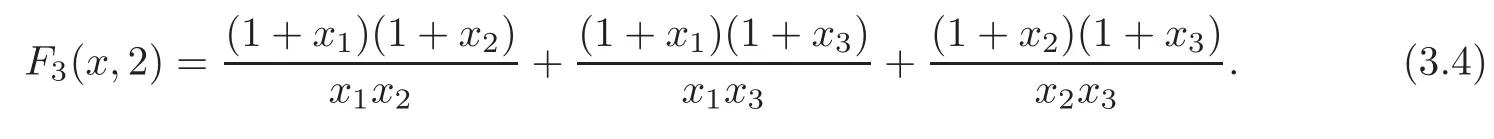
From(3.4),we have

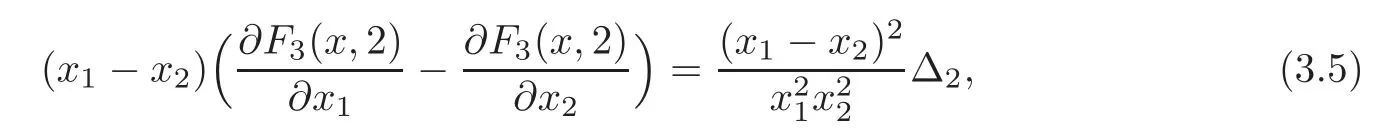
whereWhenxwe obtainHence,

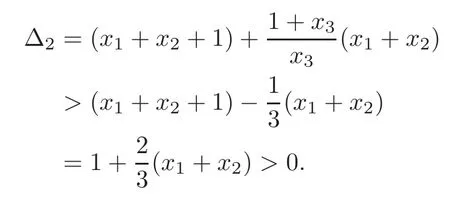
Therefore,from(3.5),we get that(3.1)holds.

Case 3 Ifn≥4,r=2,then from(1.5)we have

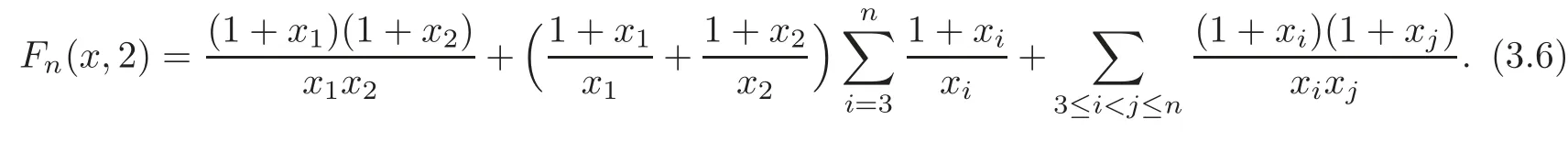
Hence,from(3.6),we get

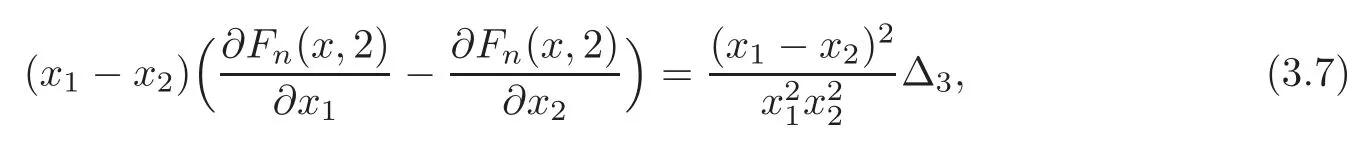
whereWhenwe haveThus

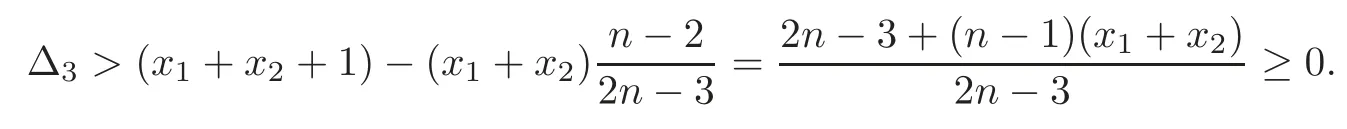
Therefore,from(3.7)we derive that(3.1)is valid.

Case 4 Ifn≥4,r=n?1,from(1.5)we have

Hence,we obtain

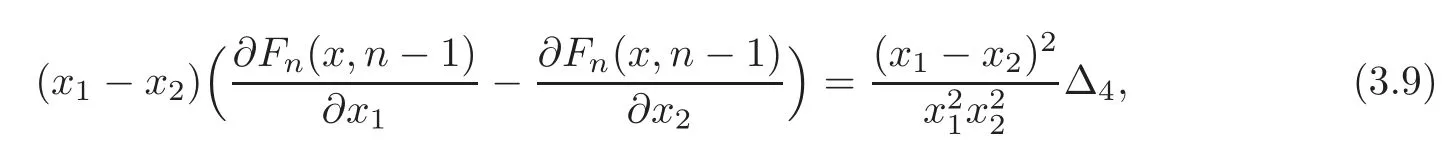
where.Whenris an even integer andwe have

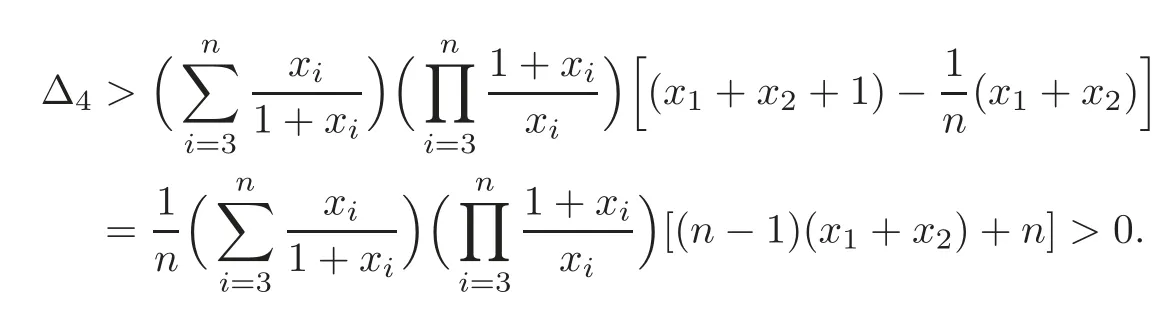
Thus,from(3.9),we have that(3.1)holds.

Case 5 Ifn≥5,3≤r≤n?2,from(1.5),we have

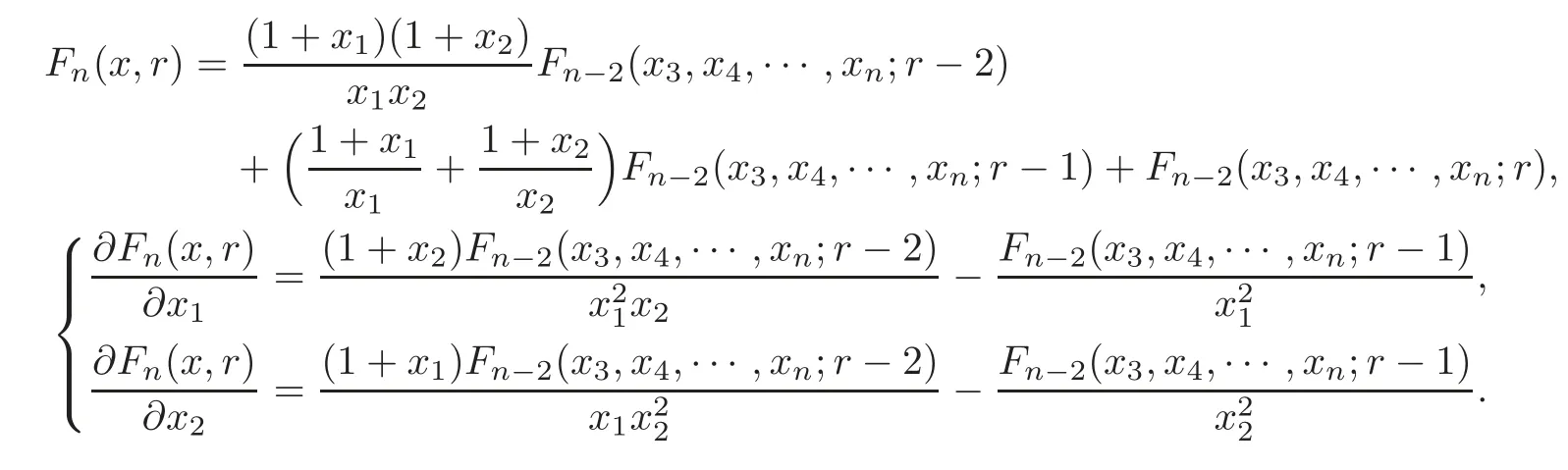
Hence,we obtain

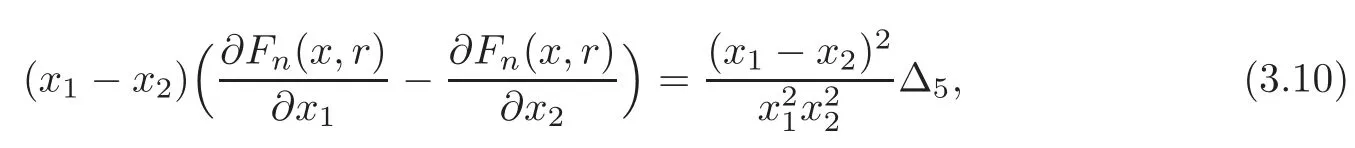
whereWhenris an even integer andwe haveFn?2(x3,x4,···,xn;r?2)＞0.From(1.5)and Lemma 2.4,we derive

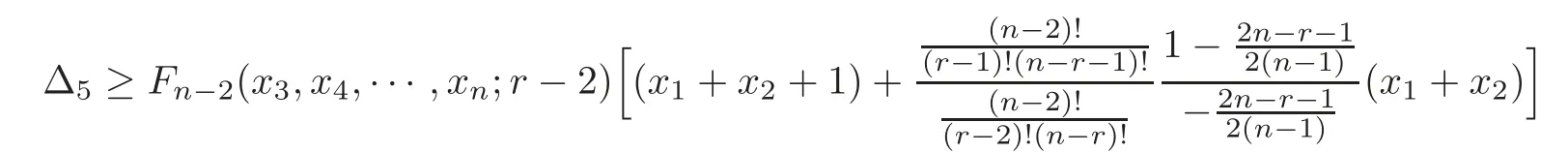
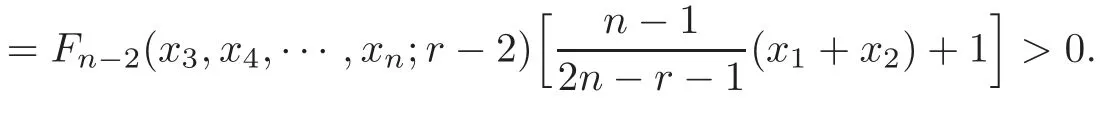
Therefore,from(3.10),we derive that(3.1)is valid.

(2)By the notations in the proof of(1),from Lemma 2.2 and Remark 2.1,we only need to prove that

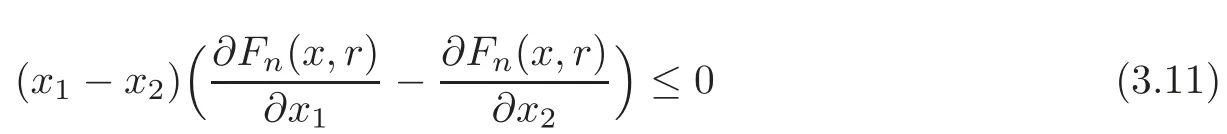
for

To prove(3.11),using the discussion similar to that of(1),we also divide the proof into five cases.

Case 1 Ifn≥2,r=n,then from(3.3)we derive Δ1≤0 forTherefore,we obtain that(3.11)holds.

Case 2 Ifn=3,r=2,andthenHence,

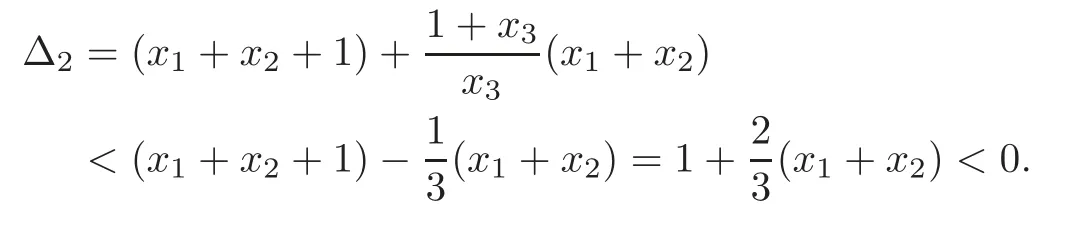
Therefore,from(3.5)we get that(3.11)holds.

Case 3 Ifn≥4,r=2,then whenwe get

Thus

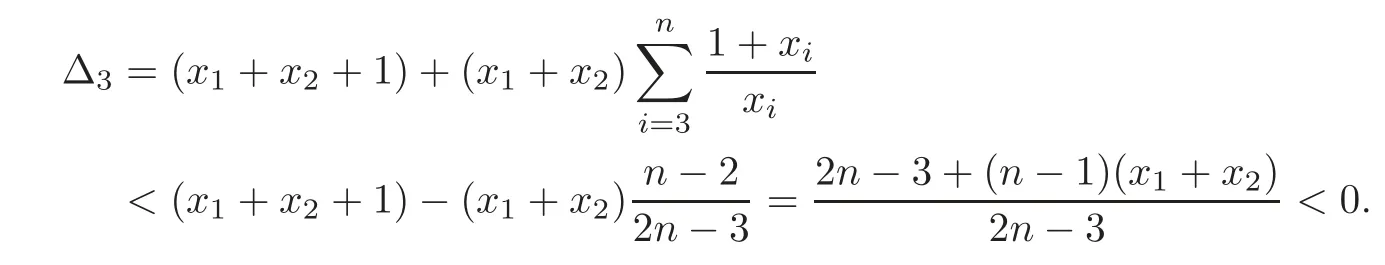
Hence,from(3.7)we obtain that(3.11)is valid.

Case 4 Ifn≥4,r=n?1,andthen

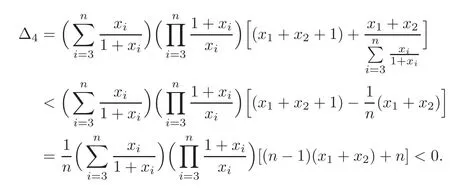
Therefore,from(3.9),we have that(3.11)holds.

Case 5 Ifn≥5,3≤r≤n?2,andthenFn?2(x3,x4,···,xn;r?2)＞0.From(1.5)and Lemma 2.4,we derive

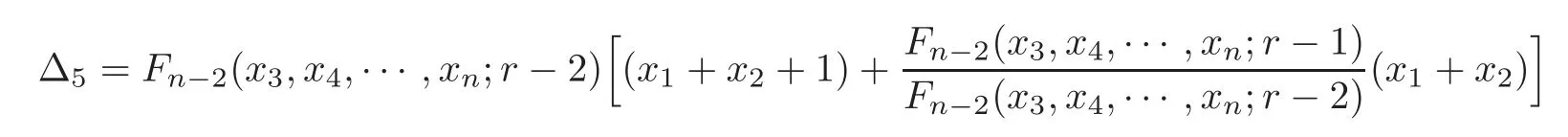
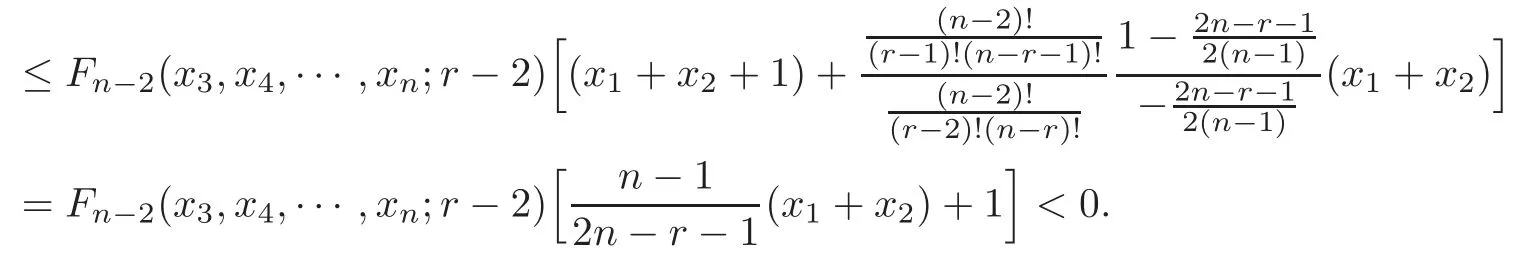
Therefore,from(3.10),we get that(3.11)is valid.

(3)According to Lemma 2.2 and Remark 2.1,from(3.3),(3.5),(3.7),(3.9)–(3.10),it is easy to see thatFn(x,r)is Schur concave in(?∞,?1]n,and Schur convex in.

This completes the proof of Theorem 3.2.

Applying Lemma 2.1 to Theorems 3.1–3.2,we can derive the Schur convexity of the symmetric functionsGn(x,r),Mn(x,r),Nn(x,r)andTn(x,r)as follows.

Theorem 3.3For n≥2,the function Gn(x,1)is Schur concave inand Schur convex in.

ProofBy replacingxijby?xijin(1.5),we get

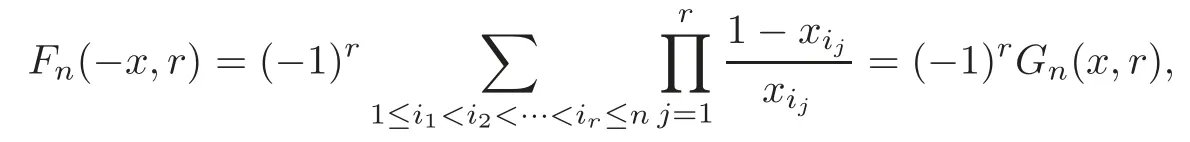
whereGn(x,r)is the symmetric function in(1.6).From Lemma 2.1 and Theorem 3.1 we obtain that Theorem 3.3 is valid.

Similarly,by replacingxijby?xijin(1.5),from Lemma 2.1 and Theorem 3.2,we can derive the following Theorem 3.4.

Theorem 3.4For n≥2,and2≤r≤n,

(1)Gn(x,r)is Schur convex inand Schur concave in

(2)if r is an even integer(or odd integer,respectively),then Gn(x,r)is Schur convex(or concave,respectively)in;

(3)if r is an even integer(or odd integer,respectively),then Gn(x,r)is schur concave(or convex,respectively)in[1,∞)n.

By substitutingxijby?1+xijin(1.5),we get

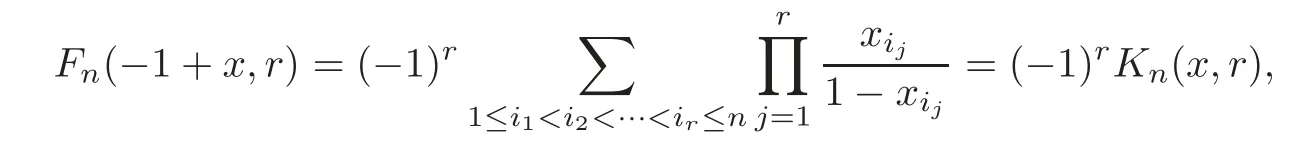
whereKn(x,r)is the symmetric function in(1.1).From Lemma 2.1 and Theorems 3.1–3.2,we can derive the following Corollaries 3.1–3.2.

Corollary 3.1For n≥2,the function Kn(x,1)is Schur concave in(1,∞)n,and Schur convex in(?∞,1)n.

Corollary 3.2For n≥2,and2≤r≤n,

(1)the function Kn(x,r)is Schur convex inand Schur concave in

(2)if r is an even integer(or odd integer,respectively),then Kn(x,r)is Schur convex(or concave,respectively)in(1,∞)n;

(3)if r is an even integer(or odd integer,respectively),then Kn(x,r)is Schur concave(or convex,respectively)in(?∞,0]n.

Remark 3.1It is easy to see that Corollaries 3.1–3.2 are the generalization of the Schur convexity ofKn(x,r)in(0,1)n,which is obtained by Guan[3]and Chu et al.[20].

Replacingxijby?1?xijin(1.5),we get

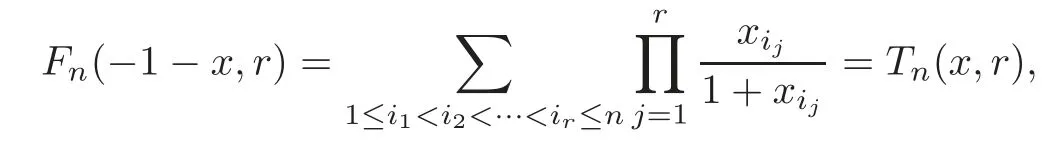
whereTn(x,r)is the symmetric function in(1.4).From Lemma 2.1 and Theorems 3.1–3.2,we can derive the following Corollaries 3.3–3.4.

Corollary 3.3For n≥2,the function Tn(x,1)is Schur concave in(?1,∞)n,and Schur convex in(?∞,?1)n.

Corollary 3.4For n≥2,and2≤r≤n,

(1)if r is an even integer(or odd integer,respectively),then Tn(x,r)is Schur convex(orconcave,respectively)in

(2)if r is an even integer(or odd integer,respectively),then Tn(x,r)is Schur concave(orconvex,respectively)in

(3)Tn(x,r)is Schur convex in(?∞,?1)n,and Schur concave in[0,∞)n.

Remark 3.2It is easy to see that Corollaries 3.3–3.4 are the generalization of the Schur convexity ofTn(x,r)in,which is obtained by Xia et al.[23].

By replacingxijbyin(1.5),from Lemma 2.1 and Theorems 3.1–3.2,we have the following Corollaries 3.5–3.6.

Corollary 3.5For n≥2,the function Mn(x,1)is Schur concave in(1,∞)n,and Schur convex in(?∞,1)n.

Corollary 3.6For n≥2,and2≤r≤n,

(1)Mn(x,r)is Schur convex inand Schur concave in

(2)if r is an even integer(or odd integer,respectively),then Mn(x,r)is Schur convex(or concave,respectively)in(1,∞)n;

(3)if r is an even integer(or odd integer,respectively),then Mn(x,r)is Schur concave(or convex,respectively)in(?∞,?1]n.

Remark 3.3It is easy to see that Corollaries 3.5–3.6 are the generalization of the Schur convexity ofMn(x,r)in(0,1)n,which is obtained by Xia and Chu[21].

By replacingxijbyin(1.5),from Lemma 2.1 and Theorems 3.1–3.2,we get the following Corollaries 3.7–3.8.

Corollary 3.7For n≥2,the function Nn(x,1)is Schur concave in(?∞,?1)n,and Schur convex in(?1,∞)n.

Corollary 3.8For n≥2,and2≤r≤n,

(1)Nn(x,r)is Schur convex inand Schur concave in

(2)if r is an even integer(or odd integer,respectively),then Nn(x,r)is Schur convex(or concave,respectively)in(?∞,?1)n;

(3)if r is an even integer(or odd integer,respectively),then Nn(x,r)is Schur concave(or convex,respectively)in[1,∞)n.

Remark 3.4It is easy to see that Corollaries 3.7–3.8 are the generalization of the Schur convexity ofNn(x,r)in(0,1)n,which is established by Xia and Chu[22].

Theorem 3.5For n≥2,and1≤r≤n,Gn(x,r)is Schur convex in Dn=｛x=(x1,x2,···,xn)

ProofAccording to Lemma 2.2 and Remark 2.1,we only need to prove that

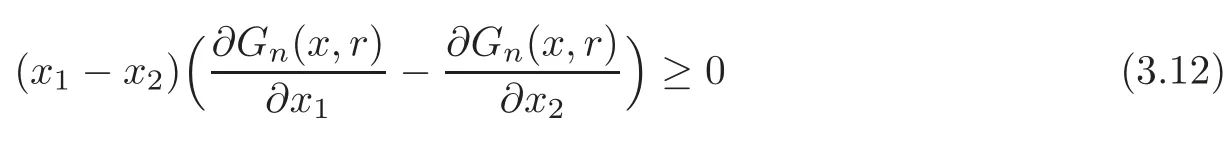
forx∈Dn.

The proof is divided into seven cases.

Case 1 Ifn≥2,r=1,from(1.6),we have

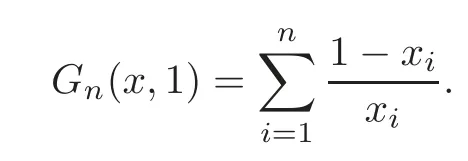
Thus we derive

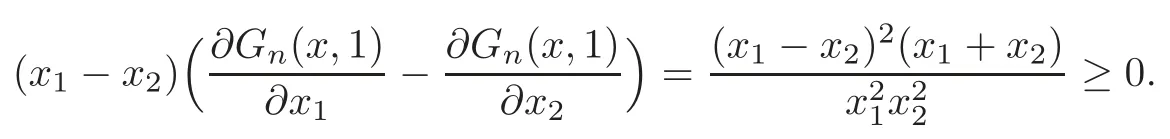
Case 2 Ifn=2,r=2,then from(1.6),we have

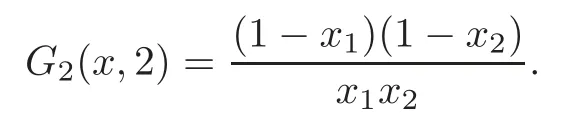
Thus we get

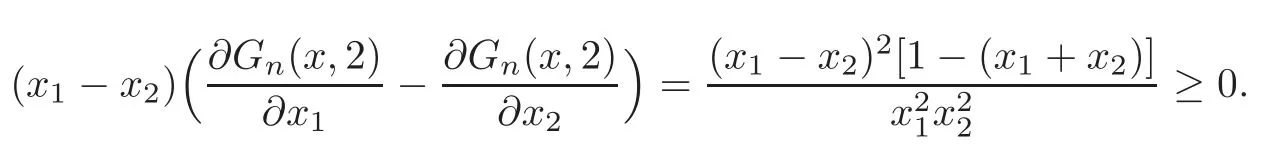
Case 3 Ifn=3,r=2,then from(1.6)we have

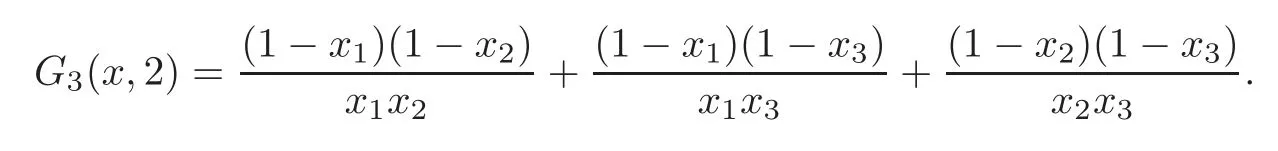
Thus we obtain

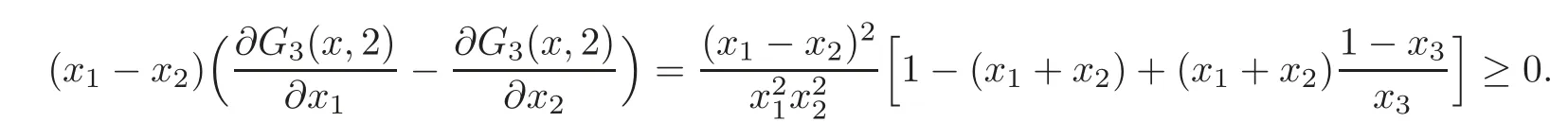
Case 4 Ifn≥4,r=n?1,then from(1.6)we have

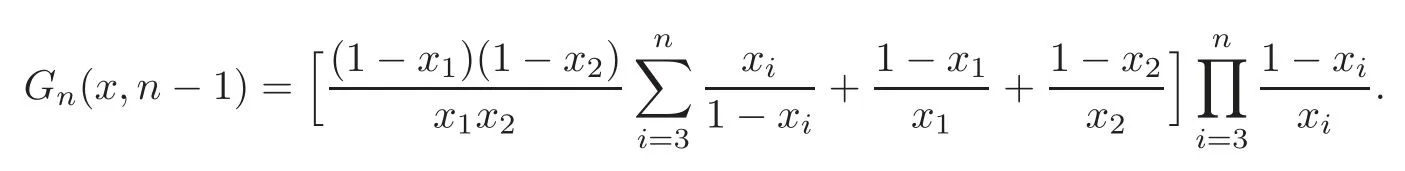
Thus we derive

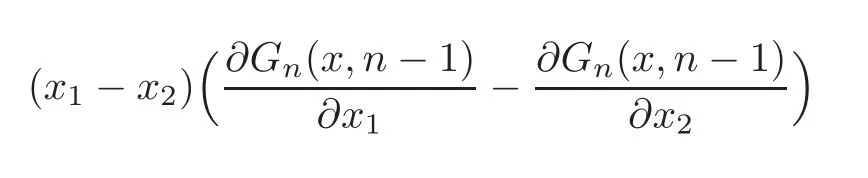
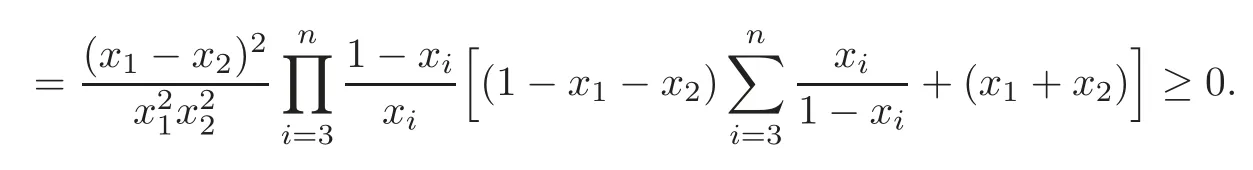
Case 5 Ifn≥4,r=2,then from(1.6)we have

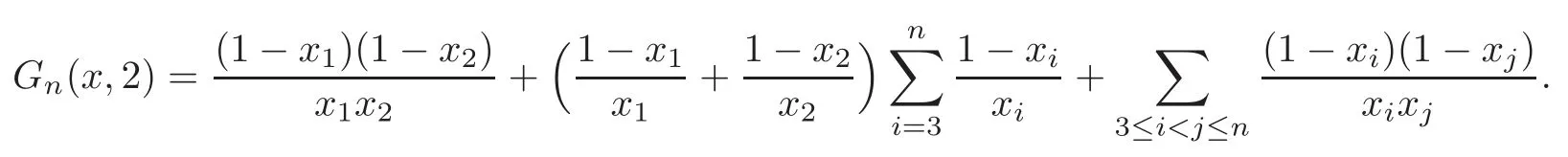
Thus we get

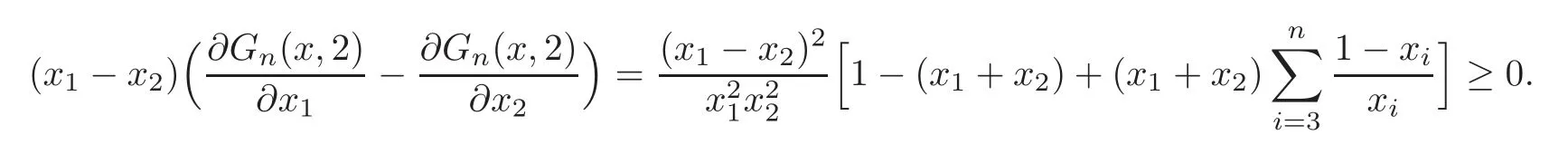
Case 6 Ifn≥3,r=n,then from(1.6),we have

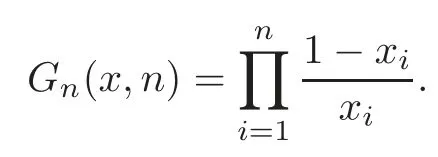
Thus we obtain

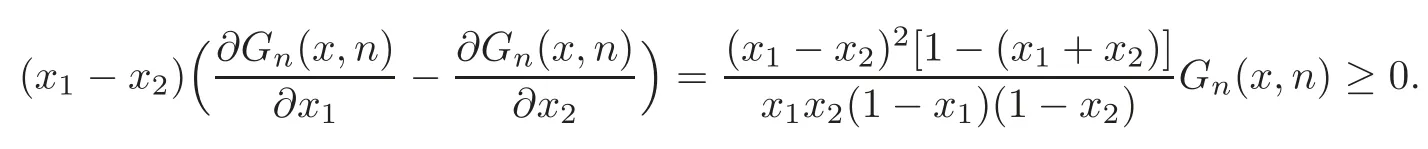
Case 7 Ifn≥5,3≤r≤n?2,then from(1.6),we have

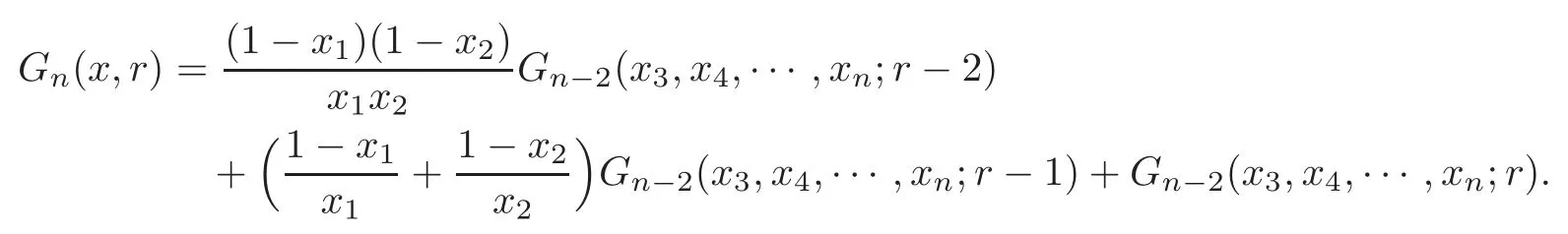
Thus we derive

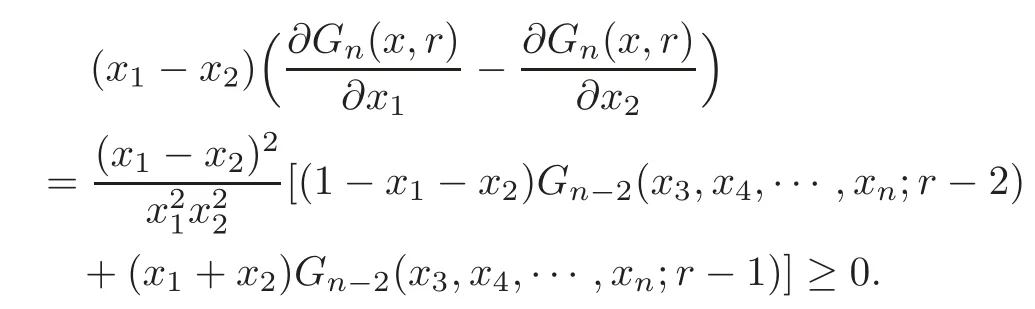
Therefore,(3.12)follows from cases 1–7,and the proof of Theorem 3.5 is completed.

4 Applications

In this section,we establish some inequalities by use of Theorems 3.1–3.5 and the theory of majorization.

Theorem 4.1If n≥2,x=(x1,x2,···,xn),

(1)Fn(x,1)≤Fn

(2)

ProofTheorem 4.1 follows from Theorem 3.1 and Lemma 2.9.

Takingλ=0 in Theorem 4.1,we have the following corollary.

Corollary 4.1If n≥2,

(1)

(2)

From Theorem 3.2 and Lemmas 2.5–2.6,we have the following result.

Theorem 4.2Let n≥2,2≤r≤n,and x=(x1,x2,···,xn)with

(1)Suppose that x∈and c≤sn.If r is even,then

while if r is odd,the inequality(4.1)is reversed.

(2)Suppose that xand c≤sn.If r is even,then(4.1)is reversed,whileif r is odd,then(4.1)is holds.

(3)Ifand c≥sn,then(4.1)holds,while if x∈(?∞,?1]nand c≤sn,then(4.1)is reversed.

Similarly,the following Theorems 4.3–4.5 can be derived from Theorem 3.2 and Lemmas 2.7–2.9 together with the fact that

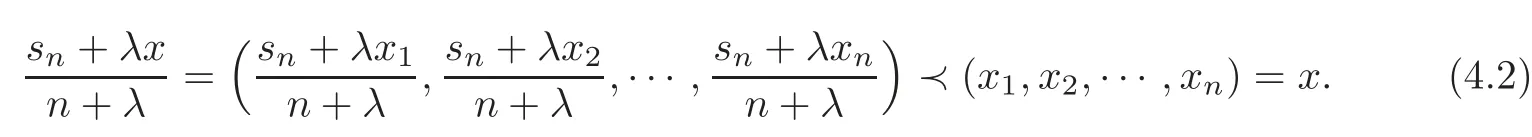
Theorem 4.3Let n≥2,2≤r≤n,and x=(x1,x2,···,xn)with

(1)Suppose that xand c≤0.If r is even,then

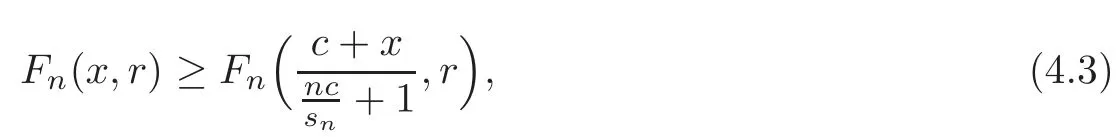
while if r is odd,then(4.3)is reversed.

(2)Suppose that xand c≤0.If r is even,then(4.3)is reversed,whileif r is odd,then(4.3)holds.

(3)If x∈and c≥0,then(4.3)holds,while if x∈(?∞,?1]nand c≤0,then(4.3)is reversed.

Theorem 4.4Let n≥2,2≤r≤n,x=(x1,x2,···,xn)withand0≤λ≤1.

(1)Suppose that xIf r is even,then

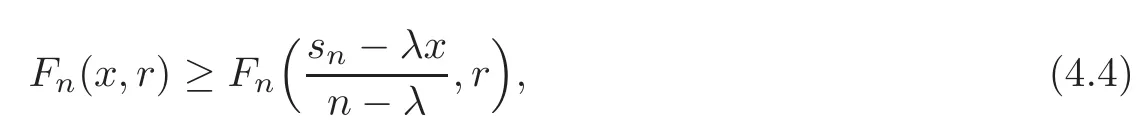
while if r is odd,then(4.4)is reversed.

(2)Suppose that xIf r is even,then(4.4)is reversed,while if r is odd,then(4.4)holds.

(3)If x∈,then(4.4)holds,while if x∈(?∞,?1]n,then(4.4)is reversed.

Theorem 4.5Let n≥2,2≤r≤n,x=(x1,x2,···,xn)withand0≤λ≤1.

(1)Suppose that xIf r is even,then

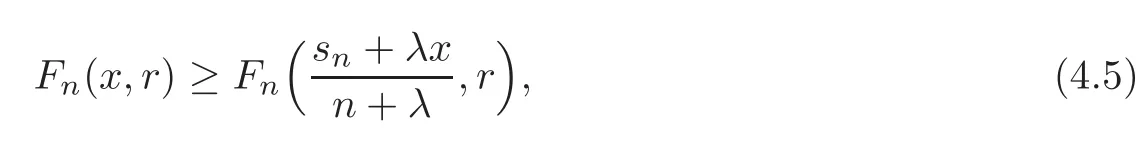
while if r is odd,then(4.5)is reversed.

(2)Suppose that xIf r is even,then(4.5)is reversed,while if r is odd,then(4.5)holds.

(3)If x∈,then(4.5)holds,while if x∈(?∞,?1]n,then(4.5)is reversed.

Takingλ=0 in Theorem 4.4 or Theorem 4.5,we derive the following theorem.

Theorem 4.6Let n≥2,2≤r≤n,x=(x1,x2,···,xn),with

(1)Suppose thatIf r is even,then

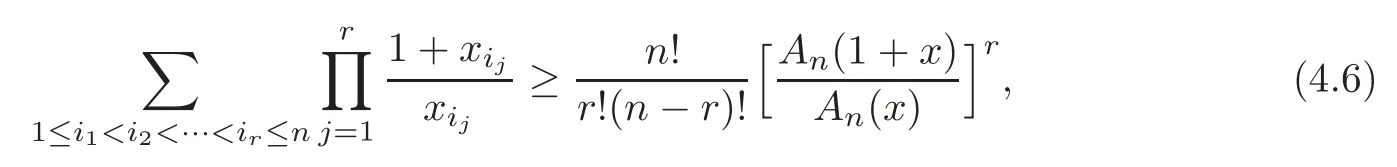
while if r is odd,then(4.6)is reversed.

(2)Suppose that xIf r is even,then(4.6)is reversed,while if r is odd,then(4.6)holds.

(3)If x∈,then(4.6)holds,while if x∈(?∞,?1]n,then(4.6)is reversed.

Remark 4.1Takingr=nandin Theorem 4.6(3),we obtain the Weierstrass inequality(see[25,p.260])

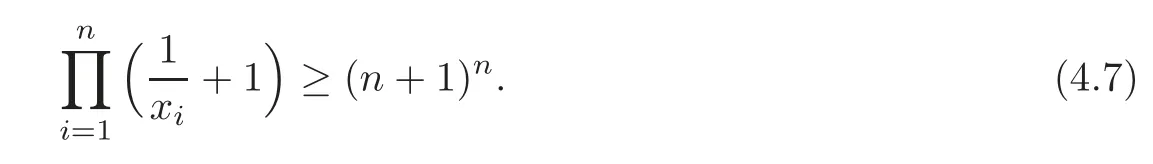
From Theorems 3.3–3.4,Lemmas 2.5–2.9,and(4.2),by an argument similar to that used in the proof of Theorems 4.1–4.5,we have the following Theorems 4.7–4.11.

Theorem 4.7Let n≥2,x=(x1,x2,···,xn)withand0≤λ≤1.Ifthen

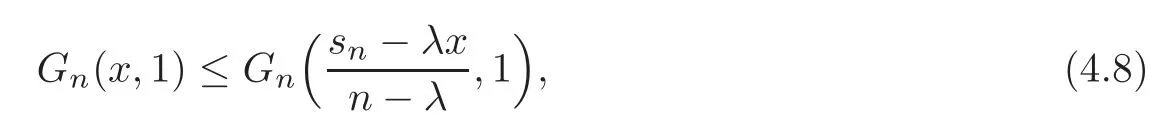
while if x∈,then(4.8)is reversed.

Takingλ=0 in Theorem 4.7,we have the following corollary.

Corollary 4.2Let n≥2,x=(x1,x2,···,xn)withthen

while if x∈,then(4.9)is reversed.

Theorem 4.8Let n≥2,2≤r≤n,x=(x1,x2,···,xn)with

(1)Suppose that c≥sn.Ifthen

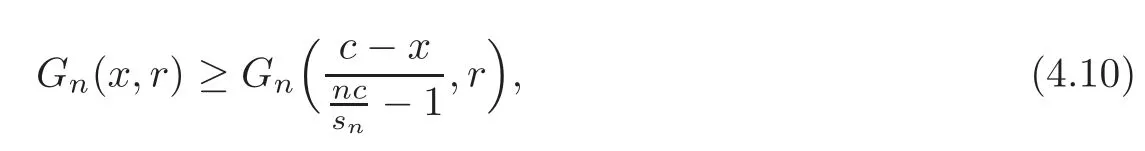
while ifthen(4.10)is reversed.

(2)Suppose that x∈and c≤sn.If r is even,then(4.10)holds,while if r is odd,then(4.10)is reversed.

(3)Suppose that x∈[1,+∞)nand c≤sn.If r is even,then(4.10)is reversed,while if r is odd,then(4.10)holds.

Theorem 4.9Let n≥2,2≤r≤n,x=(x1,x2,···,xn)with

(1)Suppose that c≥0.If

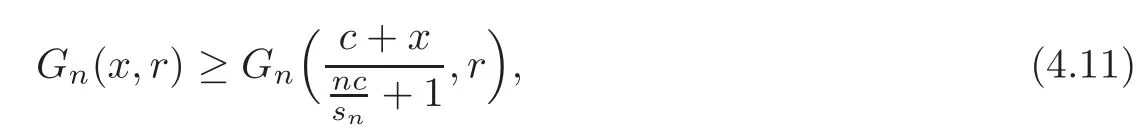
while ifthen(4.11)is reversed.

(2)Suppose that x∈and c≤0.If r is even,then(4.11)is holds,while if r is odd,then(4.11)is reversed.

(3)Suppose that x∈[1,+∞)nand c≥0.If r is even,then(4.11)is reversed,while if r is odd,then(4.11)holds.

Theorem 4.10Let n≥2,2≤r≤n,x=(x1,x2,···,xn)withand0≤λ≤1.

(1)Ifthen

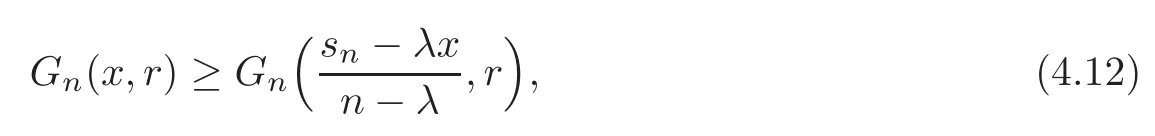
while ifthen(4.12)is reversed.

(2)Suppose that x∈.If r is even,then(4.12)holds,while if r is odd,then(4.12)is reversed.

(3)Suppose that x∈[1,+∞)n.If r is even,then(4.12)is reversed,while if r is odd,then(4.12)holds.

Theorem 4.11Let n≥2,2≤r≤n,x=(x1,x2,···,xn)withand0≤λ≤1.

(1)Ifthen

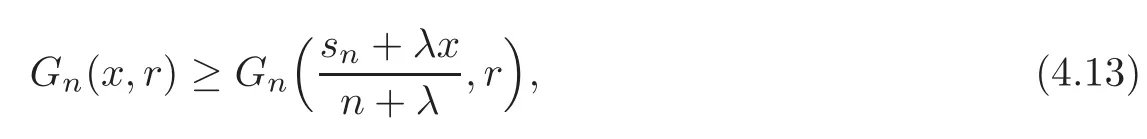
while ifthen(4.13)is reversed.

(2)Suppose that x∈.If r is even,then(4.13)holds,while if r is odd,then(4.13)is reversed;

(3)Suppose that x∈[1,+∞)n.If r is even,then(4.13)is reversed,while if r is odd,then(4.13)holds.

Takingλ=0 in Theorem 4.10 or Theorem 4.11,we derive the following theorem.

Theorem 4.12Let n≥2,2≤r≤n,x=(x1,x2,···,xn),with

(1)Ifthen

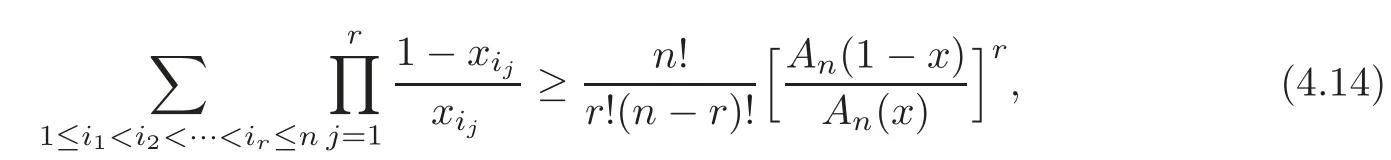
while ifthen(4.14)is reversed.

(2)Suppose that x∈.If r is even,then(4.14)holds,while if r is odd,then(4.14)is reversed.

(3)Suppose that x∈[1,+∞)n.If r is even,then(4.14)is reversed,while if r is odd,then(4.14)holds.

Remark 4.2Takingr=nin Theorem 4.12(1),we have the Ky Fan’s inequality(see[26])

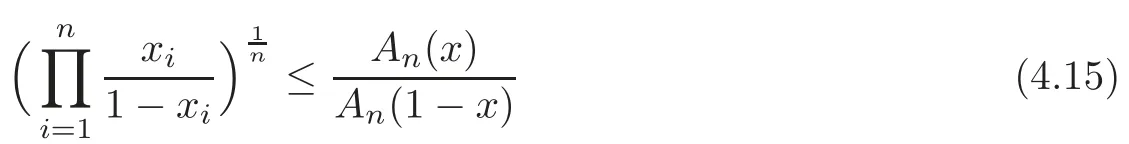
forx∈(0,]n.Inequality(4.15)has evoked the interest of several mathematicians,and different proofs as well as many extension,sharpenings,and variants have been published,see the survey paper[33]and the references therein.It is easy to see that Theorem 4.12 is a generalizations of the Ky Fan’s inequality(4.15).

Theorem 4.13Let n≥2,xi≥0(i=1,2,···,n),withThen

ProofTheorem 4.13 follows from Theorem 3.5 and the following fact

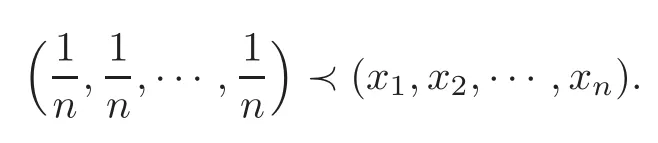
Remark 4.3Takingr=nandin Theorem 4.13,we obtain the Weierstrass inequality(see[25,p.260])

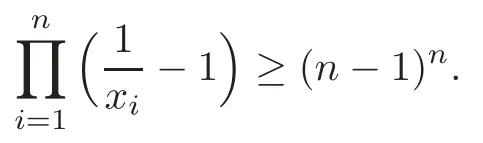
Theorem 4.14Suppose that A∈Mn(C)(n≥2)is a complex matrix,and λ1≥λ2≥···≥λnare the eigenvalues of A.If A is a positive Hermitian matrix,then

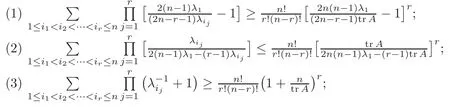
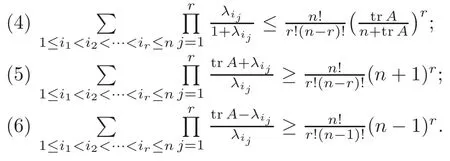
ProofIt is easy to know that

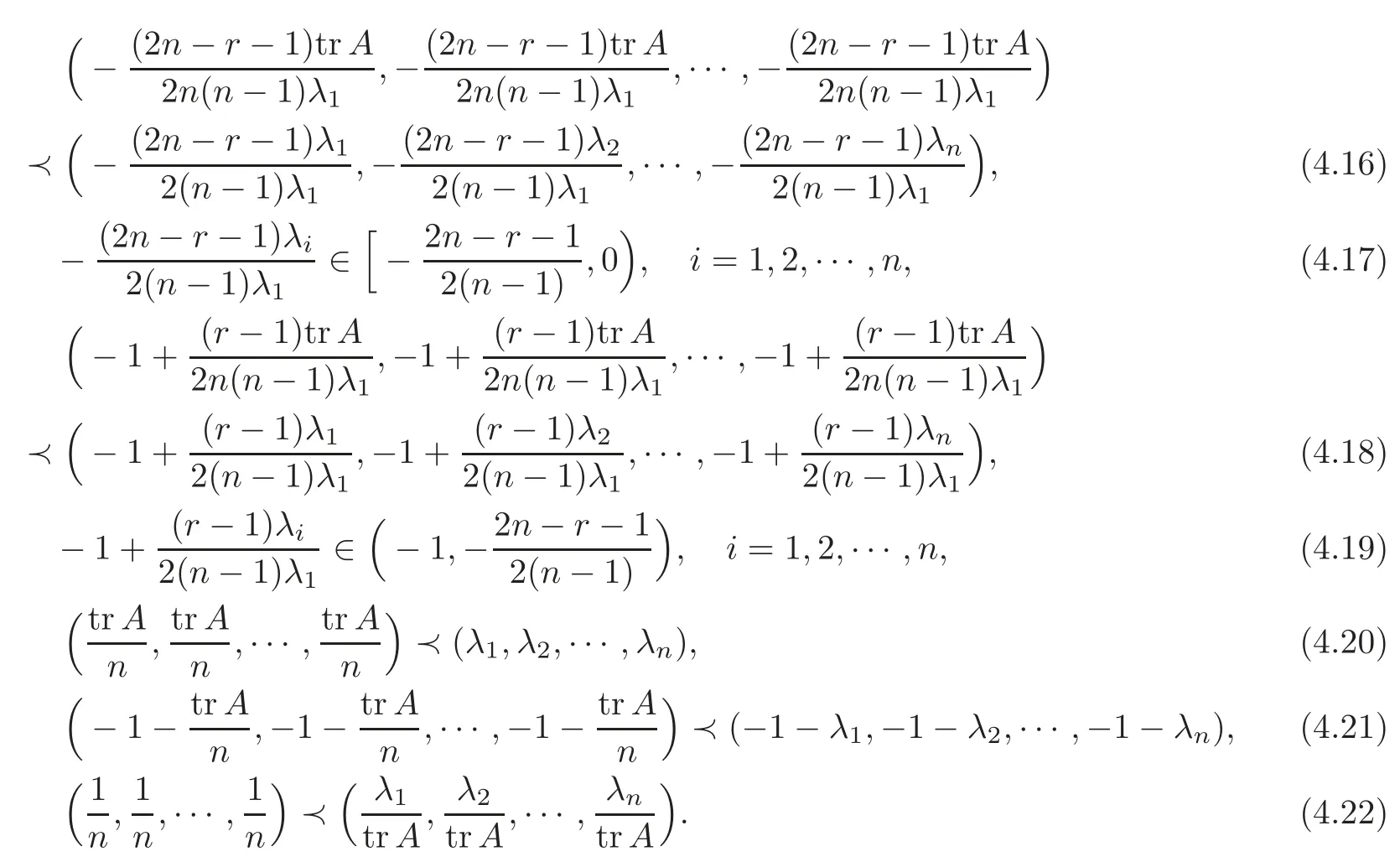
Therefore,Theorem 4.14(1)follows from(4.16)–(4.17)and Theorem 3.2(1).Theorem 4.14(2)follows from(4.18)–(4.19)and Theorem 3.2(2).Theorem 4.14(3)and Theorem 4.14(4)follow from(4.20)and(4.21)together with Theorem 3.2(3),respectively,while Theorem 4.14(5)and Theorem 4.14(6)follow from(4.22)together with Theorem 3.2(3)and Theorem 3.5,respectively.

For the proofs of Theorem 4.14(1)and Theorem 4.14(2),the reader is also referred to[20].

In 1981,Safta[27–28]proposed the following conjecture:

LetAA1,BB1,CC1be any Cevian lines in△ABC,where the pointsA1,B1,C1lie on sidesBC,CA,AB,respectively.IfAA1∩B1C1=P,BB1∩A1C1=Q,CC1∩A1B1=R,then

In[34],Zhang proved the inequality(4.23),and obtained a generalization and an improvement of this conjecture in then-dimensional space.In this paper we give a generalization of Safta’s conjecture in then-dimensional space,and obtain more extensive resuls than the main results in[34].

Theorem 4.15Let A=A1A2···An+1be an n-dimensional simples inRnand P be an arbitrary point in the interior of A.If Biis the intersection point of straight line AiP andhyperplane(i=1,2,···,n+1),and Ciis the intersectionpoint of straight line AiP and the hyperplaneΩi=B1B2···Bi?1Bi+1···Bn+1(i=1,2,···,n+1),then for r∈{1,2,···,n+1},

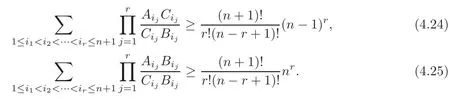
ProofLet(λ1,λ2,···,λn+1)be the barycentric coordinates of the pointP.It is easy to know that the barycentric coordinates of the pointBiareBi(λ1,λ2,···,λi?1,0,λi+1,···,λn+1).

Suppose that=θi(i=1,2,···,n,n+1).Then we have that the barycentric coordinates of the pointCiare

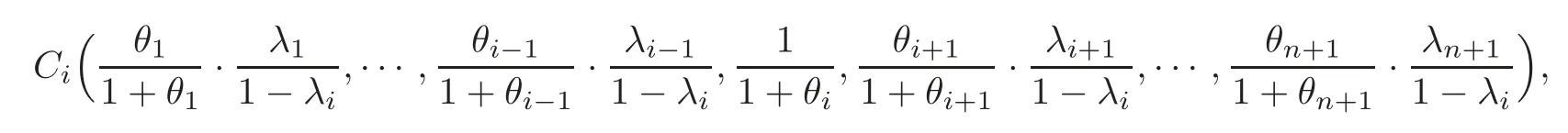
Since the pointCilie on the hyperplane Ωi,thus we have

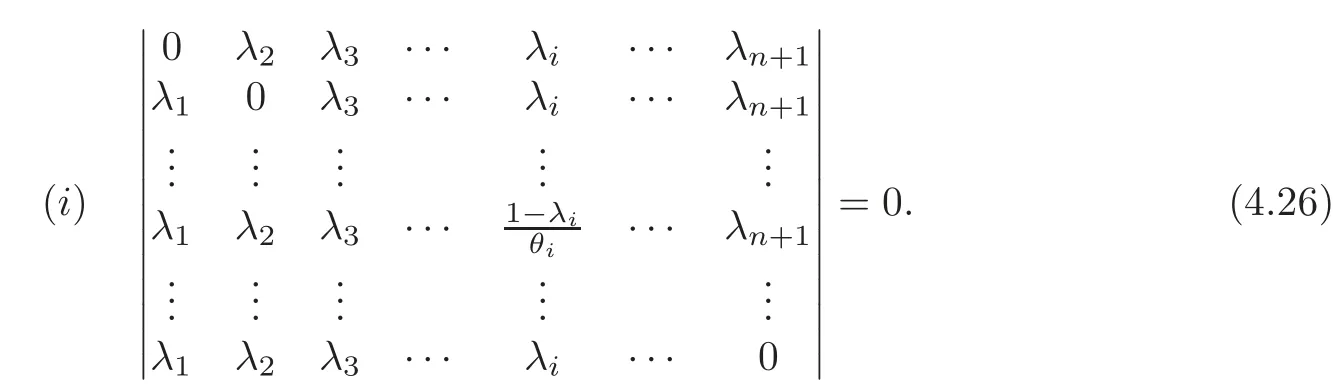
Applying the property of determinant,we can derive

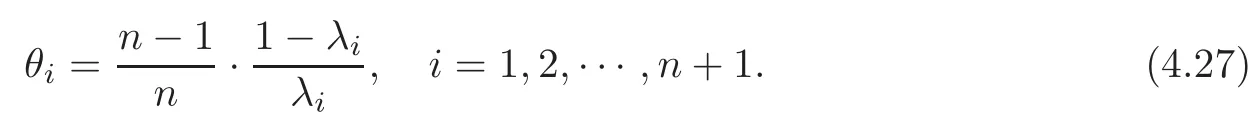
Noting thatλi＞0 andfrom(4.27),Theorem 3.5 and the fact

we have that(4.24)holds.

From(4.27),and noting the obvious fact that

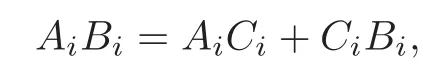
we have

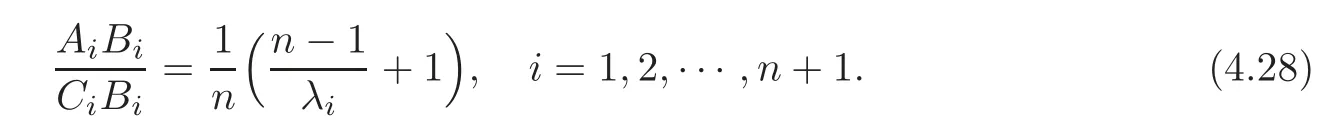
Applying(4.28),Theorems 3.1–3.2 and the fact

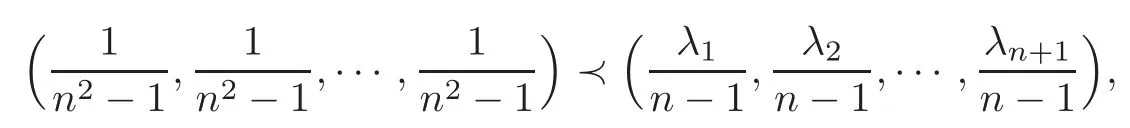
we get that the inequality(4.25)holds.

This completes the proof of Theorem 4.15.

Remark 4.4It is easy to see that Safta’s conjecture is the special case of(4.24)withn=2 andr=1,while the case ofr=nin Theorem 4.15 is the results of Theorems 1–2 in[34].Thus we give a generalization of Safta’s conjecture in then-dimensional space,and obtain more extensive results than the main results in[34].

Theorem 4.16Let A=A1A2···An+1be an n-dimensional simples inRnand P be an arbitrary point in the interior of A.If Biis the intersection point of straight line AiP andhyperplanethen for r∈{1,2,···,n+1},

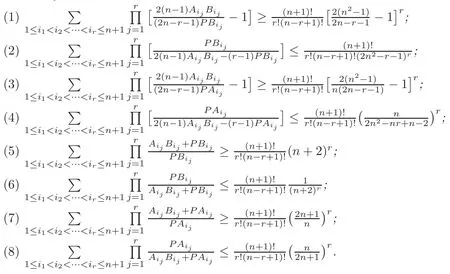
ProofIt is easy to see thatandi=1,2,···,n+1,these imply that

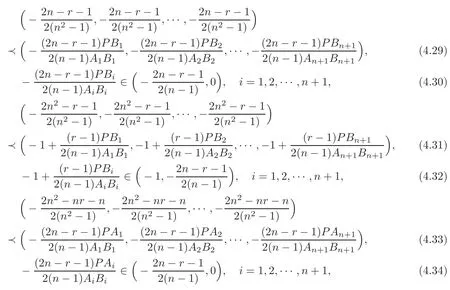
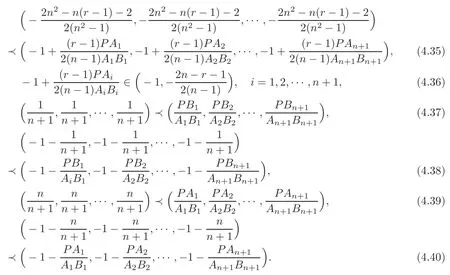
Therefore,Theorem 4.16(1)and Theorem 4.16(3)follow from(4.29)–(4.30)and(4.33)–(4.34)together with Theorem 3.2(1),respectively,Theorem 4.16(2)and Theorem 4.16(4)follow from(4.31)–(4.32)and(4.35)–(4.36)together with Theorem 3.2(2),respectively,while Theorem 4.16(5)–(8)follow from(4.37)–(4.40)and Theorem 3.2(3),respectively.

For the proofs of Theorem 4.16(1)–(4),the reader is also referred to[20],while the other proofs of Theorem 4.16(6)and Theorem 4.16(8)can be found in[23].

Remark 4.5Mitrinovi′c et al.(see[27,pp.473–479])established a series of inequalities for(i=1,2,···,n,n+1).Obviously,our inequalities in Theorem 4.16(5)and Theorem 4.16(7)are different from theirs.

AcknowledgementThe authors would like to thank the referees for valuable comments and suggestions.

[1]Schur,I.,Uber eine klasse von mittelbildungen mit anwendungen auf der determinantentheorie,Sitzungsberichte der Berliner Mathematischen Gesellschaft,22,1923,9–20.

[2]Wang,B.Y.,Foundations of Majorization Inequalities,Beijing Normal Univ.Press,Beijing,1990(in Chinese).

[3]Guan,K.,Some properties of a class of symmetric functions,J.Math.Anal.Appl.,336(1),2007,70–80.

[4]Shi,H.N.,Schur-convex functions related to Hadamard-type inequalities,J.Math.Inequal.,1(1),2007,127–136.

[5]Stepniak,C.,An effective characterization of Schur-convex functions with applications,J.Convex Anal.,14(1),2007,103–108.

[6]Zhang,X.M.,Schur-convex functions and isoperimetric inequalities,Proc.Amer.Math.Soc.,126(2),1998,461–470.

[7]Chan,N.N.,Schur-convexity forA-optimal designs,J.Math.Anal.Appl.,122(1),1987,1–6.

[8]Guan,K.Z.,The Hamy symmetric function and its generalization,Math.Inequal.Appl.,9(4),2006,797–805.

[9]Guan,K.Z.,A class of symmetric functions for multiplicatively convex function,Math.Inequal.Appl.,10(4),2007,745–753.

[10]Guan,K.Z.,Schur-convexity of the complete symmetric function,Math.Inequal.Appl.,9(4),2006,567–576.

[11]Guan,K.Z.and Guan,R.,Some properties of a generalized Hamy symmetric function and its applications,J.Math.Anal.Appl.,376(2),2011,494–505.

[12]Jiang,W.D.,Some properties of dual form of the Hamy’s symmetric function,J.Math.Inequal.,1(1),2007,117–125.

[13]Qi,F.,S′andor,J.,Dragomir,S.S.and Sofo,A.,Notes on the Schur-convexity of the extended mean values,Taiwanese J.Math.,9(3),2005,411–420.

[14]Stepniak,C.,Stochastic ordering and Schur-convex functions in comparison of linear experiments,Metrika.,36(5),1989,291–298.

[15]Hwang,F.K.and Rothblum,U.G.,Partition-optimization with Schur convex sum objective functions,SIAM J.Discrete Math.,18(3),2004,512–524.

[16]Constantine,G.M.,Schur convex functions on the spectra of graphs,Discrete Math.,45(2–3),1983,181–188.

[17]Merkle,M.,Convexity,Schur-convexity and bounds for the gamma function involving the digamma function,Rocky Mountain J.Math.,28(3),1998,1053–1066.

[18]Hwang,F.K.,Rothblum,U.G.and Shepp,L.,Monotone optimal multipartitions using Schur convexity with respect to partial orders,SIAM J.Discrete Math.,6(4),1993,533–547.

[19]Hardy,G.H.,Littlewood,J.E.and Polya,G.,Some simple inequalities satisfied by convex functions,Messenger of Mathematics,58,1929,145–152.

[20]Chu,Y.M.,Xia,W.F.and Zhao,T.H.,Schur convexity for a class of symmetric functions,Sci.China Math.,53(2),2010,465–474.

[21]Xia,W.F.and Chu,Y.M.,On Schur convexity of some symmetric functions,J.Inequal.Appl.,2010,Article ID:543250,12 pages.

[22]Xia,W.F.and Chu,Y.M.,Certain properties for a class of symmetric functions with applications,International Journal of Modern Mathematics,5(3),2010,263–274.

[23]Xia,W.F.,Wang G.D.and Chu,Y.M.,Schur convexity and inequalities for a class of symmetric functions,Int.J.Pure and Appl.Math.,58(4),2010,435–452.

[24]Chu,Y.M.,Xia,W.F.and Zhang,X.H.,The Schur concavity,Schur multiplicative and harmonic convexities of the second dual form of the Hamy symmetric function with applications,J.Multivariate Anal.,105(1),2012,412–421.

[25]Bullen,P.S.,A Dictionary of Inequalities,Longman,Harlow,1998.

[26]Beckenbach,E.F.and Bellman,R.,Inequalities,Springer-Verlag,Berlin,1961.

[27]Mitrinovi?,D.S.,Pe?ari?,J.E.and Volenec,V.,Recent Advances in Geometric Inequalities,Kluwer Academic Publishers Group,Dordrecht,1989.

[28]Safta,I.,Problem C:14,Gaz.Mat.,86,1981,224.

[29]Marshall,A.W.and Olkin,I.,Inequalities:theory of majorization and its applications,Mathematics in Science and Engineering,Vol 143,Academic Press,New York,1979.

[30]Bullen,P.S.,Handbook of Means and Their Inequalities,Kluwer Academic Publishers Group,Dordrecht,2003.

[31]Mitrinovi′c,D.S.,Analytic Inequalities,Springer-Verlag,New York,1970.

[32]Wu,S.H.,Generalization and sharpness of the power means inequality and their applications,J.Math.Anal.Appl.,312(2),2005,637–652.

[33]Alzer,H.,The inequality of Ky Fan and related results,Acta Appl.Math.,38(3),1995,305–354.

[34]Zhang,H.F.,Generalization and sharpening of Safta’s conjeture in then-dimensional space,J.Geom.,68,2000,214–217.