C.O.R.SARRICO

1 Introduction and Contents

We consider the 2×2 system of conservation laws:

wherexis the one-dimensional space variable,tis the time variable andu(x,t),v(x,t)are the unknown state variables.This system,proposed by Brio[4],appears in the study of plasmas and corresponds to the coupling of the fluid dynamic equations with Maxwell’s equations of electrodynamics.

The study of initial value problems of Riemann type for nonlinear conservation laws in spaces of distributions which include Dirac measures was initiated in 1977 by Korchinski[14]and has been widely developed in the last years(see for instance[5,8–10,12,15,21,31–33]).Recently,we have also given a contribution to this problem by showing that,in our framework,the solution of certain Riemann problems for the Brio system can develop a delta shock wave(see[30]).

Letδbe the Dirac measure concentrated at the origin.In the present paper we subject the Brio system to the initial conditionsu(x,0)=c0δ(x),andv(x,0)=h0δ(x)(withc0,h0∈R,c0≠0,h0≠0).We will prove that,in a convenient space of distributions and under certain compatibility conditions,three types of solutions for this problem arise:

(1)u(x,t)=c0δ(x?st),v(x,t)=h0δ(x?st);

(2)u(x,t)=

(3)u(x,t)=

The first one is a travelling delta wave with speedThe second and third ones are not measures;they are singular perturbations which propagate with speed 1(indeed,the third one is not a solution but a family of solutions parametrized by an arbitrary numberλsuch thatc0λ＞0).It is worth to be noted that in each of those solutions the quantitiesare conserved.

Thus we can conclude that,for the Brio system with initial conditions involving Dirac masses,the space of measures is not suffcient to contain all solutions of this problem.It is interesting to note that the space of discontinuous functions is not suffcient to contain all solutions of the Brio system with discontinuous functions as initial conditions as we have proved in[30].

A very interesting theory of delta shock waves with Dirac measures developing in both state variables for a class of nonstrictly hyperbolic systems of conservation laws was recently established by Yang and Zhang in[33].We refer the reader to this important paper which has extensive references strongly related to this subject.

In the literature different concepts of a solution can be found:The measure theoretic method(see[1–2,5,11]),use of smooth function nets and weighted measure spaces(see[13]),split delta functions(see[19,22]),Colombeau generalized functions(see[20]),the weak asymptotic method(see[9–10]),and others.

Our concept of a solution is defined within the setting of our theory of distributional products;here the product of two distributions is always a distribution and it is not defined by approximation processes.Our products depend upon the choice of a certain functionαthat encodes the indeterminacy inherent to products.Naturally,such an indeterminacy may appear,or not,in the outcoming of differential equations or systems.We call such solutionsα-solutions.The occurrence of these solutions may be interpreted as a selection made by the physical system;in certain cases,this selection can not be previously known owing to some features of the physical system that were not considered in the formulation of the model.We stress that this indeterminacy is not,in general,avoidable and in many situations it also has a physical meaning.Concerning this point let us mention[3,6–7,24].It goes without saying that,also in a classical context,sometimes one is led to impose on the nonlinear model extra conditions(such as entropy conditions)to make the model more adherent to physical situations and allow a decrease of the indeterminacy.

Let us present some results we have obtained within the framework of our distributional products.

For the conservation lawut+[φ(u)]x=ψ(u),whereφ,ψare entire functions taking real values on the real axis,we have established(see[28])necessary and suffcient conditions for the propagation of a travelling wave with a given distributional profile and we have also computed its speed.For example,for LeVeque and Yee equation(φ(u)=uandwithμ/=0)we have proved that there exist six travelling waves with the profilec1+(c2?c1)H(c1,c2are constants andHstands for the Heaviside function),all of them with speed 1.Whenψ=0 andφ′′≠0,we conclude that the only continuous travelling waves are the constant states.Thus,if we ask for nonconstant travelling waves for the conservative equationut+[φ(u)]x=0,withφ′′≠0 we have to seek them among distributions that are not continuous functions;for wave profiles that areC1-functions with one jump discontinuity,our methods lead us easily to the well-known Rankine-Hugoniot conditions.

Conditions for the propagation of wave profilesβ+mδandβ+mδ′(whereβis a continuous function,m∈R,andm≠0)as well as their speeds were also obtained(see[29]).For example,for the diffusionless Burgers-Fischer equation

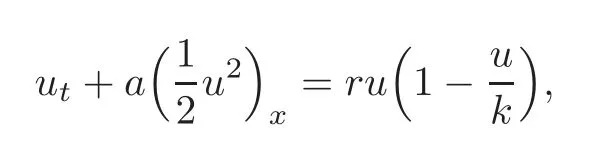
wherea＞0,r＞0 andk＞0,the profileb+mδ(whereb∈R)can arise as a travelling wave if and only ifb=0 orb=kwith wave speedin both cases.For the Burgers conservative equationthe profileβ+mδ′can arise as a travelling wave if and only ifβ=bis a constant function and the wave speed isb.

In the setting of soliton wave collision,we are able to prove that delta waves under collision behave just as classical soliton collisions(as in the Korteweg-de Vries equation)in models ruled by a singular perturbation of the Burgers conservative equation(see[26]).Also,the phenomenon of gas dynamics,known as “infinitely narrow soliton solution”,discovered by Maslov and his collaborators(see[16–18]),can be described directly in distributional form(see[25]).

Let us summarize the contents of the present paper.In Section 2,we present a brief survey about our products of distributions in order to introduce the reader into this framework and keep computations self-contained.These formulas are presented without proofs.The reader can obtain a general view of our distributional products in Sections 2–3 of[24].The details are given in[23].In Section 3,we define the concept of anα-solution for the Brio system.We stress that this concept can be viewed as a consistent extension of the concept of a classical solution.Finally,in Section 4,we define a convenient space of distributionsWand we compute allαsolutions of the Brio system that belong toWand satisfy the initial conditionsu(x,0)=c0δ(x),andv(x,0)=h0δ(x).

2 Products of Distributions

LetDbe the space of indefinitely differentiable complex-valued functions defined on R,with compact support,andD′be the space of Schwartz distributions.In our theory a certain functionα∈Dwithaffords a productT˙αSofT,S∈D′.When agreement with the usual Schwartz product of distributions with functions is desirable,as in the sequel,theα-product must be restricted to certain spaces of distributions to be singled out,as described below.

Ourα-products are bilinear and satisfy the propertywhereτameans the usual translation operator in the distributional sense.Ifαis even theα-products are also transformed as usual by the symmetryt?tfrom R onto R.In general associativity and commutativity do not hold(recall that the products of distributions defined by Schwartz are not in general associative).Theα-products can not be completely localized:Indeed,supp(T˙αS)?suppSas for usual functions,but it may happen that supp(T˙αS)/?suppT.Thus,ourαproducts are to be viewed as global entities and they are consistent with Schwartz products ofD′p-distribution withCp-functions(if these ones are placed on the right-hand side).Theαproducts satisfy the usual differential rules including the Leibniz formula that must be written in the form

Here we suppose thatT˙αS,(DT)˙αSandT˙α(DS)are defined by(2.1),(2.6)or(2.7)below.

In this section we only give formulas for three kinds ofα-products which will be noted by the unique symbolT˙αSbecause they are mutually compatible(details for theα-products(2.1)and(2.6)can be seen in[24];for theα-product(2.7),see[27]).

The first one can be evaluated by the formula

forT∈D′p,andwhereis the space of distributions of order≤pin the sense of Schwartz,(D′∞meansD′),is the space of distributions whose support has Lebesgue measure zero,Tβis the usual Schwartz product of aD′p-distribution with aCp-function and(T?α)fis the usual product of aC∞-function with a distribution.For instance,ifβis a continuous function,we have,for anyα,

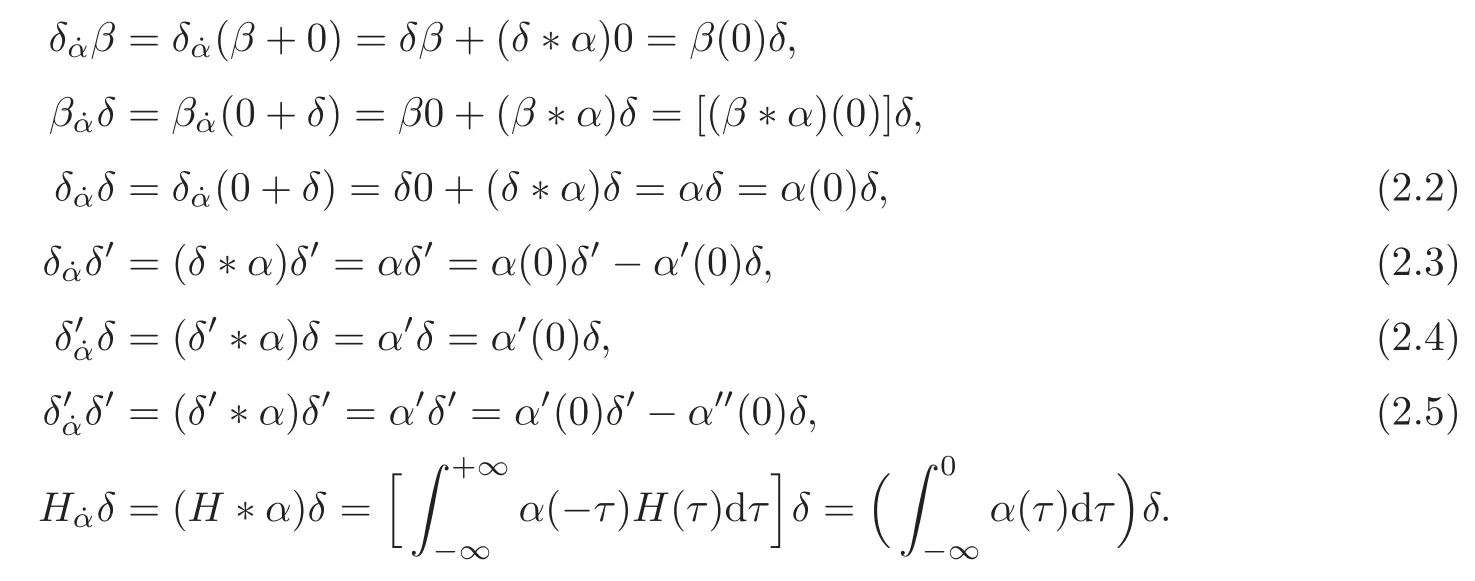
The second one is to be computed by the formula

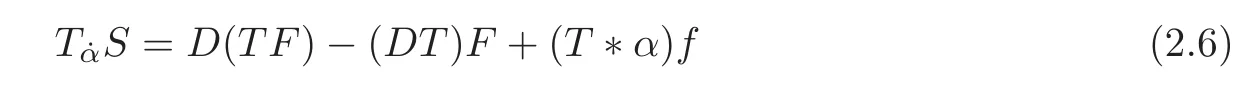
forT∈D′?1andwhereD′?1stands for the space of distributionsT∈D′such thatDT∈D′0,andF∈C0is such thatDF=w(so,locally,Tcan be read as a function of bounded variation andFas an absolutely continuous function).In[24],we have proved thatT˙αSgiven by(2.6)is independent of the choice of the functionFsuch thatDF=w.For instance,sinceH∈D′?1andwe have

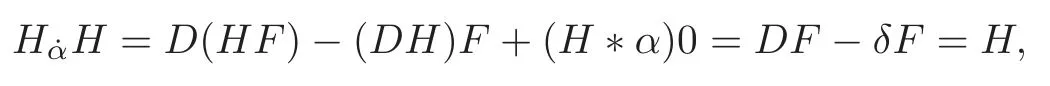
takingF:R→R defined byF(x)=0 forx≤0 andF(x)=xforx＞0.More generally,ifT∈D′?1andS∈L1loc,then we haveT˙αS=TS(see[27,p.1002]for a proof).We want to stress that in(2.1)or(2.6)the convolutionT?αis not to be understood as an approximation ofT.Those formulas are to be considered as exact ones.

The thirdα-product can be computed by the formula

forwhereis the space of distributions,the support of which is at most countable,andY∈D′?1is such thatDY=T(the productsY˙αSandY˙α(DS)are supposed to be computed by(2.1)or(2.6)).The value ofT˙αSgiven by(2.7)is independent of the choice ofY∈D′?1such thatDY=T(see[27,p.1004]for the proof).For instance,we have for anyα,

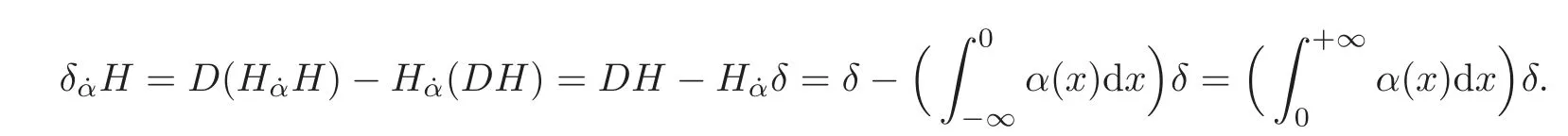
3 The Concept of α-Solution for the Brio System

LetIbe an interval of R with more than one point and letF(I)be the space of continuously differentiable maps:I→D′in the sense of the usual topology ofD′.Fort∈I,the notation(x)is sometimes used to emphasize that the distribution(t)acts on functionsξ∈Dwhich depend onx.

Let Σ(I)be the space of functionsu:R×I→C such that

(a)for eacht∈I,u(x,t)∈(R);

(b):I→D′defined by(x)=u(x,t)is inF(I).

The natural injectionuof Σ(I)intoF(I)allows us to identify any function in Σ(I)with a certain map inF(I).SinceC1(R×I)?Σ(I),we can write the inclusions

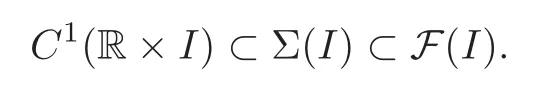
The identif i cationuallows us to write the Brio system(1.1)–(1.2)in the form:

Definition 3.1Given α,the pair∈F(I)×F(I)will be called an α-solution of the system(3.1)–(3.2)on I,if the α-products that appear in these equations are well defined and both equations are satisfied for all t∈I.

We have the following results.

Theorem 3.1If(u,v)is a classical solution of(1.1)–(1.2)onR×I,then,for any α,the pair∈F(I)×F(I)defined by(x)=u(x,t)and(x)=v(x,t),is an α-solution of(3.1)–(3.2)on I.

Remark 3.1By a classical solution of(1.1)–(1.2)on R×I,we mean a pair(u(x,t),v(x,t))ofC1-functions that satisfies(1.1)–(1.2)on R×I.

Theorem 3.2If u,v:R×I→Care C1-functions and,for a certain α,the pair∈F(I)×F(I)defined by[(t)](x)=u(x,t)and[(t)](x)=v(x,t),is an α-solution of(3.1)–(3.2)on I,then the pair(u,v)is a classical solution of(1.1)–(1.2)onR×I.

For the proof,it is enough to observe that anyC1-functionu(x,t)can be read as a continuously differentiable function∈F(I)defined by[(t)](x)=u(x,t)and to use the consistency of theα-products with the classical Schwartz products.

If we changetoin the equation(3.2),we obtain the equation

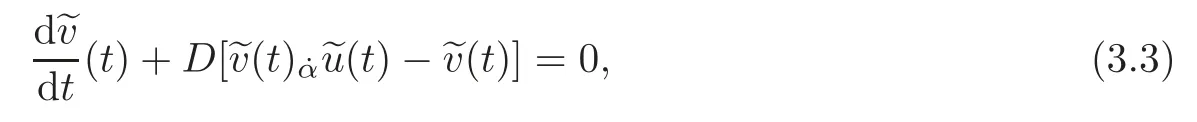
which is not equivalent to(3.2),since ourα-products are not,in general,commutative.However,all that we have said above for the systems(1.1)–(1.2)and(3.1)–(3.2)are also valid for the systems(1.1)–(1.2)and(3.1)–(3.3).Thus,in order to simplify the language,we will callαsolution of the system(1.1)–(1.2)anα-solution of the system(3.1)–(3.2),or of the system(3.1)–(3.3).Hence,anα-solution in this sense affords a consistent extension of the concept of a classical solution of the system(1.1)–(1.2).

4 Dirac Masses as Initial Conditions

As we have said in the introduction,we have already applied our framework to prove that the solution of a Riemann problem for the Brio system can develop aδ-shock wave.This suggests as to consider the possible formation of aδ′-shock wave from initial conditions that contain Dirac masses.

Thus,let us consider the Brio system(1.1)–(1.2)with(x,t)∈R×R and the unknownsu(x,t)andv(x,t)submitted to the initial conditions:

wherec0,h0∈R withc0≠0 andh0≠0.We will compute allα-solutions of this problem which belong to the following spaceW:The pair∈W,if and only if∈F(R)and there existC1-functionsc,f,h,γ:R→R such that

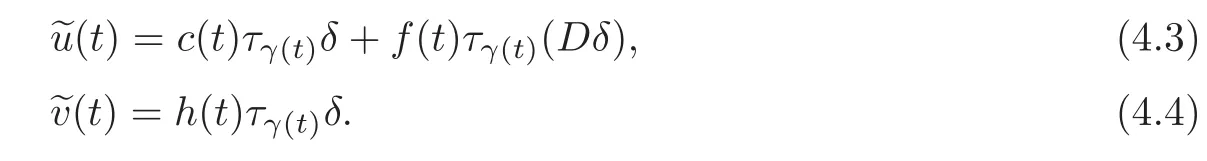
Clearly we can also consider more general initial conditions and more general spaces of solutions.Meanwhile,the calculations are much longer and our choice is a simple way to see that the space of measures is not suffcient to contain allα-solutions of this problem!

In the sequel,we will apply the following result.

Lemma 4.1Let us consider the initial value problem

where a,b∈Rand b≠0.Then this problem has a global solution y∈C1(R)if and only if≤0.We also have

(b)the unique global solution is y(t)=

ProofIf=0,the proof is trivial.For＜0,let us consider the change of the unknowny(t)z(t)defined by

We haveand(4.5)–(4.6)turn out to be

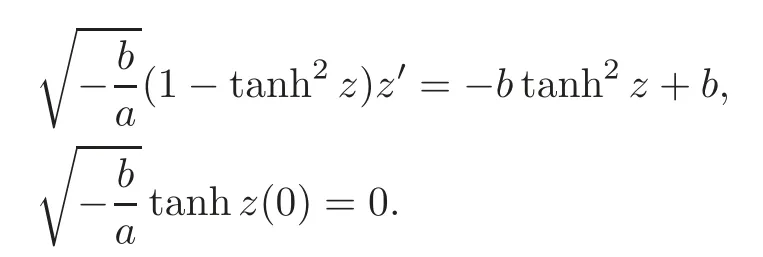
This problem is equivalent to the initial value problemwhich has the unique solutionhence(b)follows from(4.7).For＞0,(4.5)is equivalent to the equationwhich can be easily solved by separation of variables.The unique solution

defined in any interval]?ε,ε[withcan not be extended to all R as aC1-function and we have not a global solution in this case.The statement is proved.

Now,let us consider the problem(3.1)–(3.2)submitted to the initial conditions(0)=c0δand(0)=h0δwhich are,inF(R),the conditions corresponding to(4.1)–(4.2):

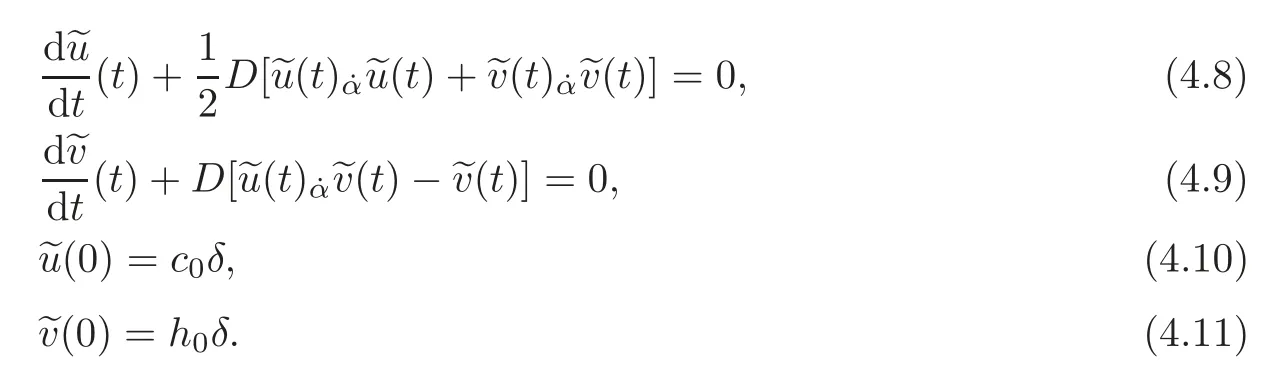
We have the following result.

Theorem 4.1Given α,the initial value problem(4.8)–(4.11)has an α-solution in W precisely if and only if any of the following three conditions(each one of them excludes the others)is satisfied:

(I)

(II)=α(0),α′(0)=0,α′′(0)=0;

(III)

Under(I)the unique α-solution in W is given bywith

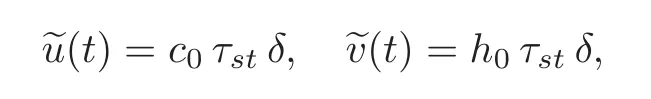
where s

Under(II)the unique α-solution in W is given bywith

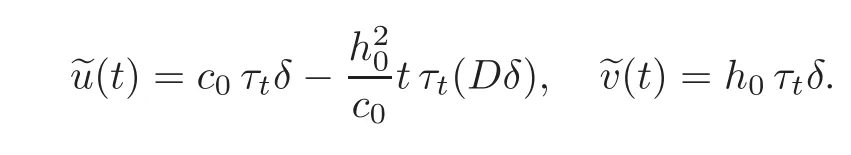
Under(III)the unique α-solution in W is given bywith

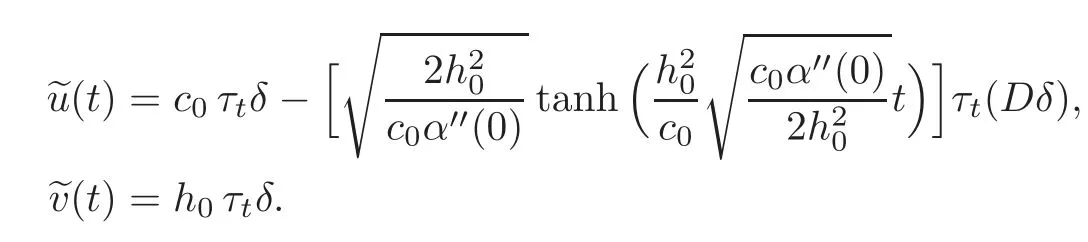
ProofClearly,(I)excludes(II)and(III)since the equalityimpliesh0=0 which is impossible.The other exclusions are obvious.

Let us suppose∈W.Then by(4.3)–(4.4),we have

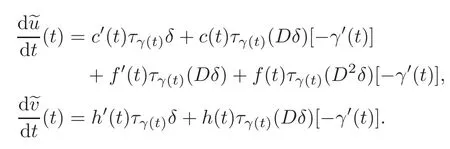
Applying(2.2)–(2.5)when necessary,we also have

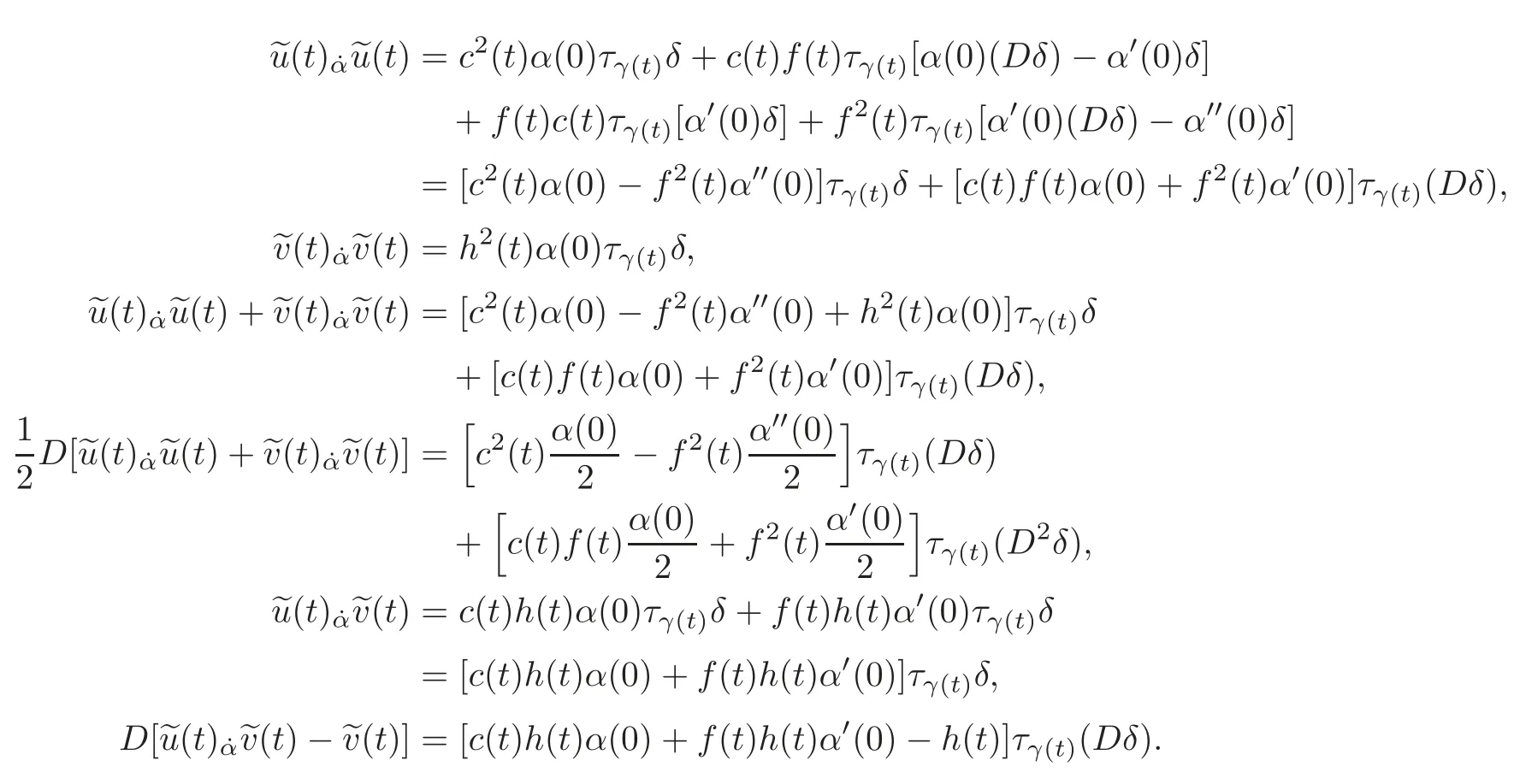
Thus,the problem(4.8)–(4.11)has anα-solution inWif and only if,for allt∈R,the following four equations are satisfied:

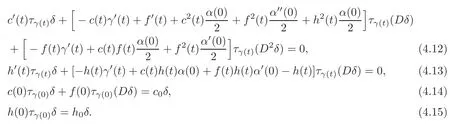
As a consequence,the problem(4.8)–(4.11)has anα-solution inWif and only if,for allt∈R,the following conditions are satisfied:

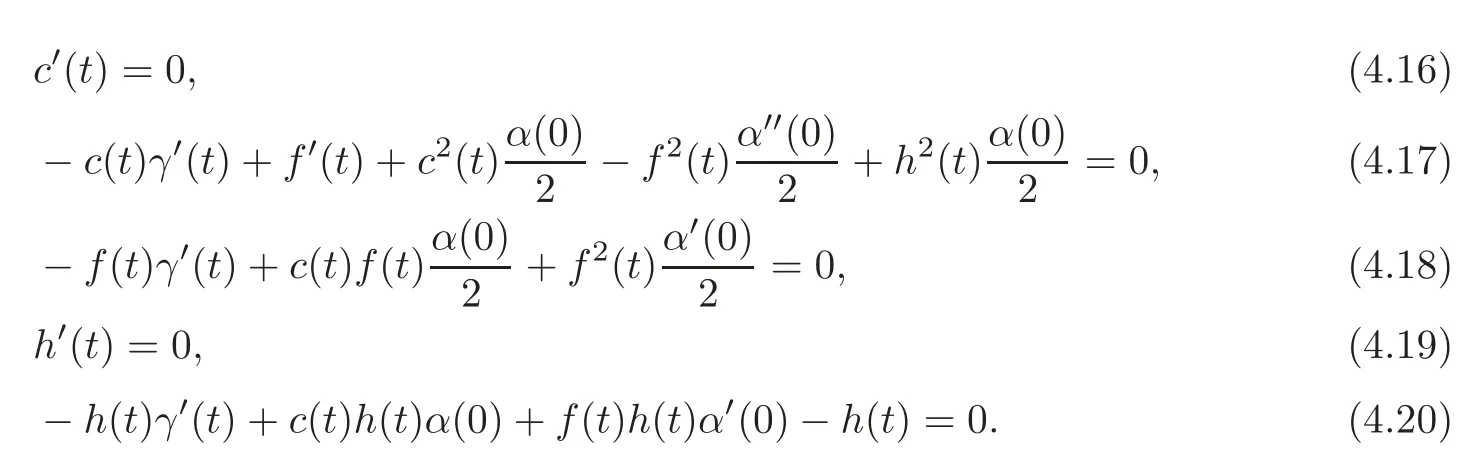
From(4.14)we conclude thatf(0)=0.Thus,c(0)τγ(t)δ=c0δand it is easy to see thatc(0)=c0andγ(0)=0.From(4.15)we conclude thath(0)=h0andγ(0)=0 as well.Conditions(4.16)and(4.19)jointly withc(0)=c0andh(0)=h0enable us to conclude thatc(t)=c0andh(t)=h0for allt∈R.Thus,(4.17)–(4.18)and(4.20)turn out to be

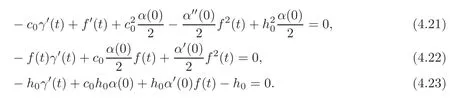
From(4.23),it follows

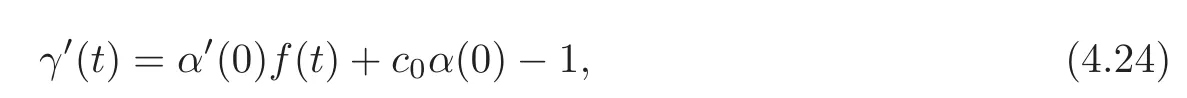
and(4.21)–(4.22)turn out to be

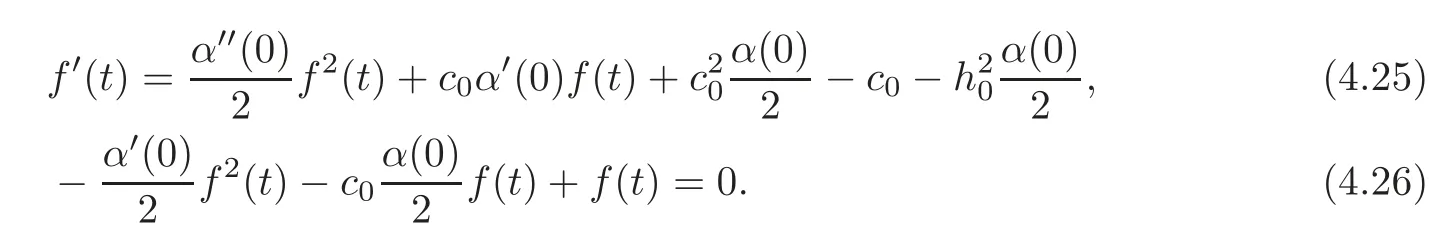
Taking the derivative of(4.26),we have,for allt∈R,

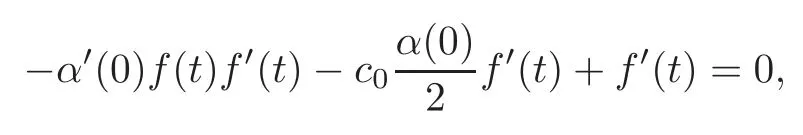
and from the particular valuet=0 we obtain

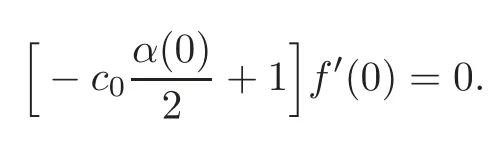
Thus,we have two possibilities:

Let us supposef′(0)=0.Then puttingt=0 in(4.25)we obtainand this means thatandThus,(4.24)–(4.26)give

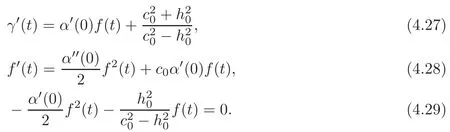
Now,ifα′(0)=0,from(4.29)we havef(t)=0 for allt∈R and from(4.27)we obtainIfα′(0)/=0,from(4.29)we have

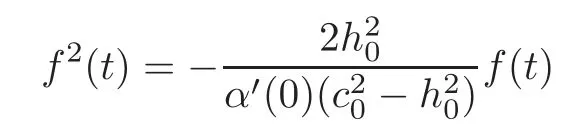
and(4.28)turns out to be

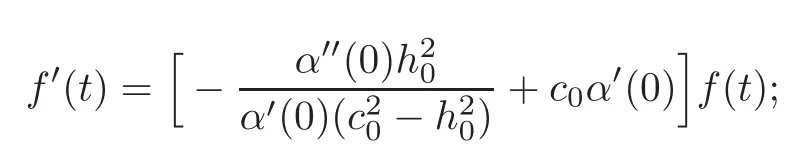
this differential equation with the initial conditionf(0)=0 has the unique solutionf(t)=0 for allt∈R,which leads once more tosinceγ(0)=0,case(I)follows.

Let us supposeα(0)=Then(4.24)–(4.26)turn out to be

From(4.31)we know thatf(t)does not vanish identically andα′(0)=0 follows from(4.32);then,we can write(4.30)–(4.31)in the form:

From(4.33)andγ(0)=0 we conclude thatγ(t)=t;from(4.34)andf(0)=0 we conclude,applying Lemma 4.1,that:

(a)Ifα′′(0)=0,thenf(t)=

(b)Ifc0α′′(0)＞0,thenf(t)=tanh

Cases(II)and(III)follow immediately.

This theorem furnishes three types ofα-solutions of the problem(1.1)–(1.2),(4.1)–(4.2).These solutions,subjected to the admissibility conditions already specif i ed,read thus:

(1)u(x,t)=

(2)u(x,t)=c0δ(x?t)?

(3)u(x,t)=c0δ(x?t)?

The first one is a travelling delta wave with speedand the second and third ones are not measures.Also remark that the first and second ones do not depend on the choice ofα;the third one is a family of solutions parametrized by an arbitrary numberα′′(0)such thatc0α′′(0)＞0.

About the interpretation of the physical occurrence of anα-solution we have already mentioned it in the introduction.

The next theorem deals with the same problem for the Brio system by reversing in(4.9)the order of factorsit is an interesting feature that only solutions of the first type are obtained.Thus,let us solve inWthe problem(4.8),(3.3),(4.10),(4.11),which,due to the noncommutativity of our product,does not coincides with the problem(4.8)–(4.11)we have considered above.We have the following result.

Theorem 4.2Given α,the initial value problem(4.8),(3.3),(4.10),(4.11)has an α-solutionin W if and only ifThis α-solution is unique in W and is given bywith

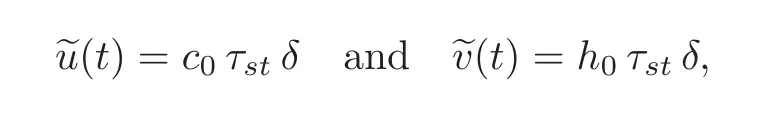
where s

ProofLet us suppose∈W.Then,by applying(2.2)–(2.3),we have

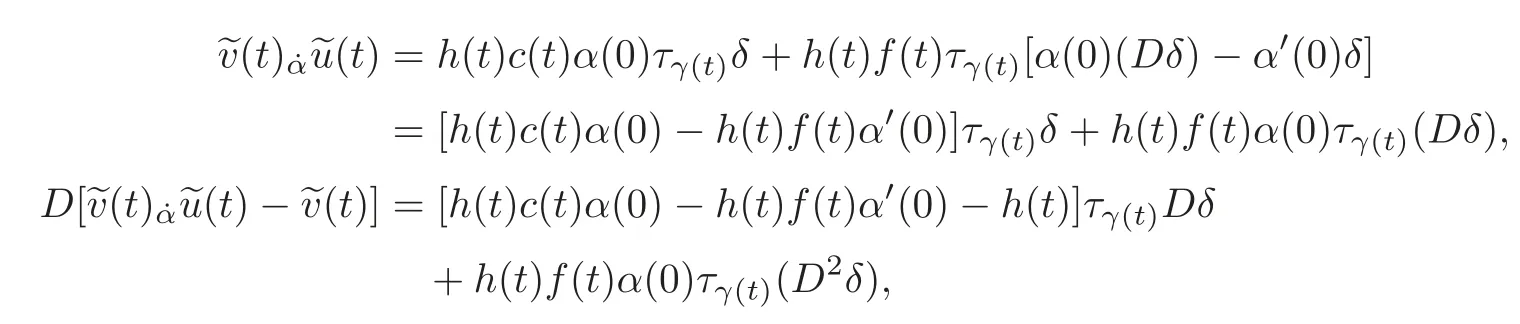
so that(3.3)turns out to be

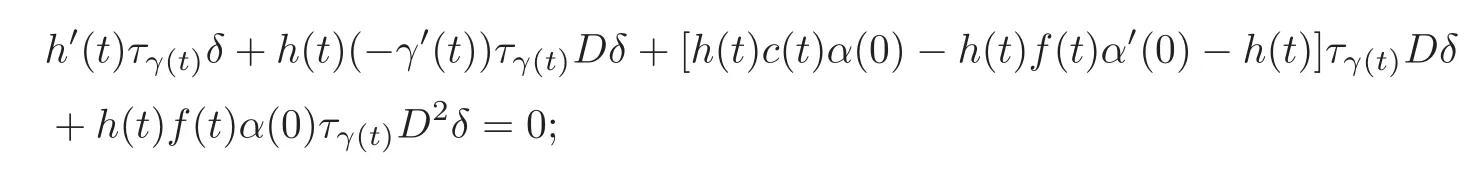
this means that the problem(4.8),(3.3),(4.10),(4.11)has anα-solution inWif and only if the conditions(4.12)and(4.14)–(4.15)are satisfied together with the condition

As a consequence,we conclude thatf(0)=0,c(0)=c0,γ(0)=0,h(0)=0 and also that the following conditions are to be satisfied(they correspond to conditions(4.16)–(4.20)of the previous theorem):

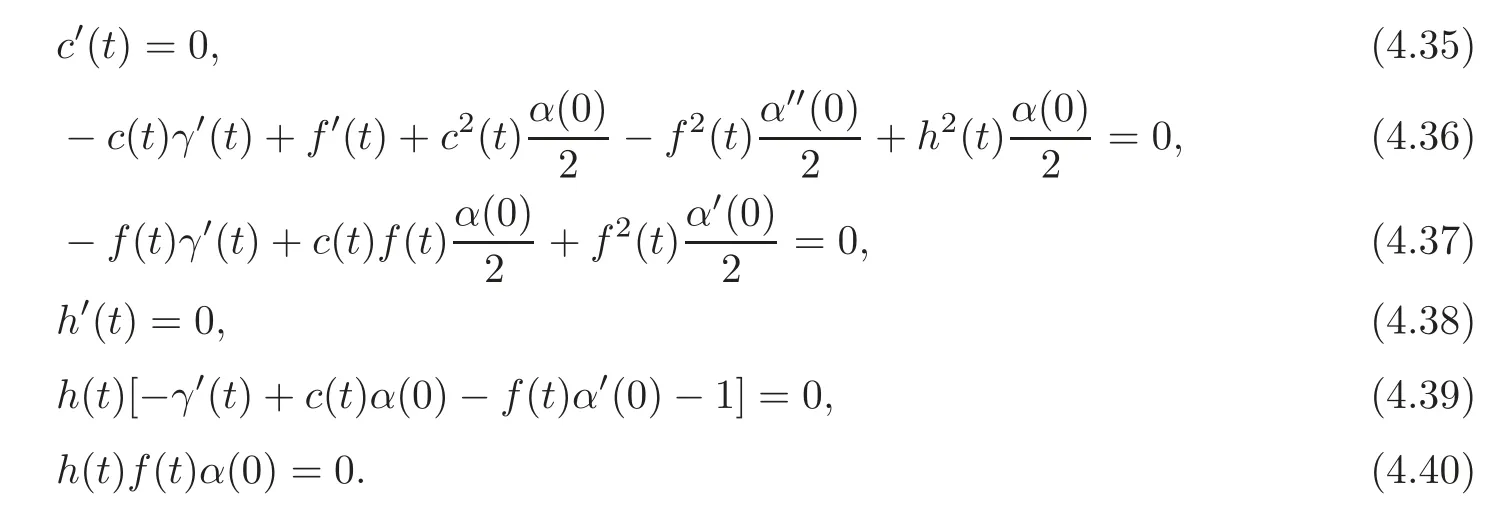
From(4.35)and(4.38)we conclude thatc(t)=c0andh(t)=h0,and(4.36)–(4.37)and(4.39)–(4.40)turn out to be

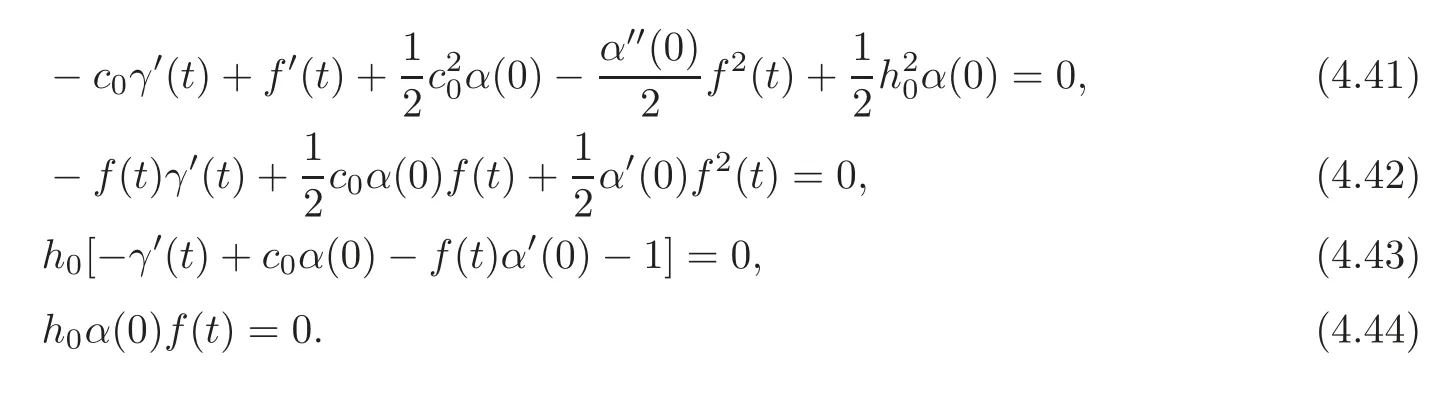
From(4.44)we haveα(0)=0 orf(t)=0 for allt∈R.Now,we will see that we can not haveα(0)=0.Indeed,ifα(0)=0,(4.41)–(4.43)would read

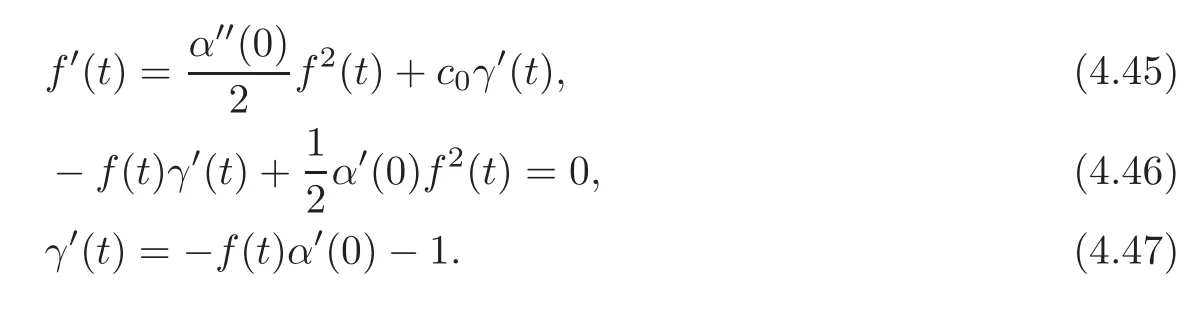
Applying(4.47)we can write(4.46)in the form:

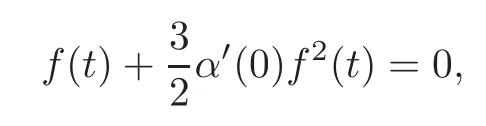
and taking the derivative,we have,for allt∈R,f′(t)+3α′(0)f(t)f′(t)=0.Puttingt=0 we conclude thatf′(0)=0.Now,puttingt=0 in(4.45)and(4.47),we obtain 0=c0γ′(0)andγ′(0)=?1,which is a contradiction.

As a consequence,we havef(t)=0 for allt∈R,and from(4.41)and(4.43),we obtain

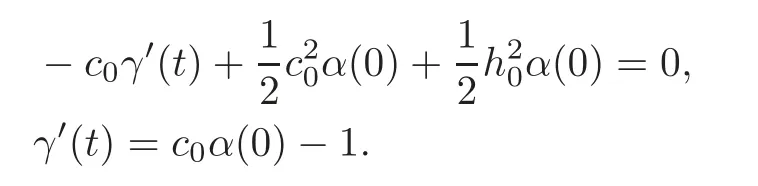
This linear system in the unknownsα(0)andγ′(t)has a solution,just,

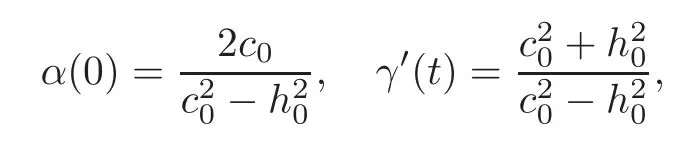
if and only ifThe statement follows immediately.

Thus,this theorem does not introduce moreα-solutions for the problem(1.1),(1.2),(4.1),(4.2)and we conclude that allα-solutions for this problem were given in Theorem 4.1.

A final remark.We know that there exist nonlinear systems for which the singular solutions,as obtained by approximation,are exactly the same as those obtained within our distributional framework.However,for the Brio system,we don’t know if it is possible to obtain the results of the present paper by approximation.In this setting,and in several cases,the solutions are strongly affected by the process of approximation chosen.

AcknowledgementsThe author is grateful to Prof.Vaz Ferreira of Bologna University for his help in the preparation of this paper during his visit at this institution.The author is also thankful to the referee for the suggestions which have helped to improve and clarify the text.

[1]Bouchut,F.and James,F.,Duality solutions for pressureless gases,monotone scalar conservation laws,and uniqueness,Comm.PDE,24,1999,2173–2190.

[2]Brenier,Y.and Grenier,E.,Sticky particles and scalar conservation laws,SIAM J.Numer.Anal.,35,1998,2317–2328.

[3]Bressan,A.and Rampazzo,F.,On differential systems with vector-valued impulsive controls,Bull.Un.Mat.Ital.Ser.B,2(7),1988,641–656.

[4]Brio,M.,Admissibility conditions for weak solutions of nonstrictly hyperbolic systems,Proc.Int.Conf.on Hyperbolic Problems,Springer-Verlag,Berlin,1988.

[5]Chen,G.Q.and Liu,H.,Formation of delta shocks and vacuum states in the vanishing pressure limit of solutions to Euler equations for isentropic fluids,SIAM J.Math.Anal.,34,2003,925–938.

[6]Colombeau,J.F.and Le Roux,A.,Multiplication of distributions in elasticity and hydrodynamics,J.Math.Phys.,29,1988,315–319.

[7]Dal Maso,G.,LeFloch,P.and Murat,F.,Def i nitions and weak stability of nonconservative products,J.Math.Pures Appl.,74,1995,483–548.

[8]Danilov,V.G.and Mitrovic,D.,Weak asymptotic of shock wave formation process,Nonlinear Analysis:Theory,Methods and Applications,61,2005,613–635.

[9]Danilov,V.G.and Shelkovich,V.M.,Dynamics of propagation and interaction of shock waves in conservation law systems,J.Differential Equations,211,2005,333–381.

[10]Danilov,V.G.and Shelkovich,V.M.,Delta shock wave type solution of hyperbolic systems of conservation laws,Q.Appl.Math.,29,2005,401–427.

[11]Huang,F.,Weak solutions to pressureless type system,Comm.PDE,30,2005,283–304.

[12]Joseph,K.T.,A Riemann problem whose viscosity solutions containsδ-measures,Asymptot.Analysis,7,1993,105–120.

[13]Keyfitz,B.L.and Kranzer,H.C.,Spaces of weighted measures for conservation laws with singular shock solutions,J.Differential Equations,118,1995,420–451.

[14]Korchinski,C.,Solution of a Riemann problem for a 2×2 system of conservation laws possessing no classical weak solutions,Ph.D.Thesis,Adelphi University,1977.

[15]LeVeque,R.J.,The dynamics of pressureless dust clouds and delta waves,J.Hyperbolic Diff.Eq.,1,2004,315–327.

[16]Maslov,V.P.,Nonstandard characteristics in asymptotical problems,Russian Math.Surveys,38(6),1983,1–42.

[17]Maslov,V.P.and Omel’yanov,G.A.,Asymptotic soliton-form solutions of equations with small dispersion,Russian Math.Surveys,36(3),1981,73–149.

[18]Maslov,V.P.and Tsupin,V.A.,Necessary conditions for existence of infinitely narrow solitons in gas dynamics,Soviet Phys.Dock,24(5),1979,354–356.

[19]Nedeljkov,M.,Unbounded solutions to some systems of conservation laws-split delta shock waves,Mat.Ves.,54,2002,145–149.

[20]Nedeljkov,M.,Delta and singular delta locus for one-dimensional systems of conservation laws,Math.Method.Appl.Sci.,27,2004,931–955.

[21]Nedeljkov,M.,Shadow waves:Entropies and interactions of delta and singular shocks,Archives Rat.Mech.Anal.,197,2010,489–537.

[22]Nedeljkov,M.and Oberguggenberger,M.,Interactions of delta shock waves in a strictly hyperbolic system of conservation laws,J.Math.Anal.Appl.,334,2008,1143–1157.

[23]Sarrico,C.O.R.,About a family of distributional products important in the applications,Port.Math.,45,1988,295–316.

[24]Sarrico,C.O.R.,Distributional products and global solutions for nonconservative inviscid Burgers equation,J.Math.Anal.Appl.,281,2003,641–656.

[25]Sarrico,C.O.R.,New solutions for the one-dimensional nonconservative inviscid Burgers equation,J.Math.Anal.Appl.,317,2006,496–509.

[26]Sarrico,C.O.R.,Collision of delta-waves in a turbulent model studied via a distribution product,Nonlinear Analysis,73,2010,2868–2875.

[27]Sarrico,C.O.R.,The multiplication of distributions and the Tsodyks model of synapses dynamics,Int.J.of Math.Analysis,6(21),2012,999–1014.

[28]Sarrico,C.O.R.,Products of distributions and singular travelling waves as solutions of advection-reaction equations,Russian J.of Math.Phys.,19(2),2012,244–255.

[29]Sarrico,C.O.R.,Products of distributions,conservation laws and the propagation ofδ′-shock waves,Chin.Ann.Math.,33B(3),2012,367–384.

[30]Sarrico,C.O.R.,The Riemann problem for the Brio system:A solution containing a Dirac mass obtained via a distributional product,submitted.

[31]Sheng,W.and Zhang,T.,The Riemann problem for transportation equations in gas dynamics,Mem.Amer.Math.Soc.,137,1999,1–77.

[32]Tan,D.,Zhang,T.and Zheng,Y.,Delta shock waves as a limits of vanishing viscosity for a system of conservation laws,J.Differential Equations,112,1994,1–32.

[33]Yang,H.and Zhang,Y.,New developments of delta shock waves and its applications in systems of conservation laws,J.Differential Equations,252,2012,5951–5993.