Weijun LU

1 Introduction

Geometric flows are important in many fields of mathematics and physics.A geometric flow is an evolution of a geometric structure under a differential equation related to a functional on a manifold,usually associated with some curvatures.The most popular geometric flows in mathematics are the heat flow(see[12,18]),the Ricci flow(see[3,6,21]),the mean curvature flow(see[26])and the Yamabe flow(see[1–2,5,20,25]).

The subject of Hamilton’s Ricci flow(see[9]):lies in the more general field of geometric fl ows,which in turn lies in the even more general field of geometric analysis.In Ricci flow we see the unity of geometry and analysis.As a fully nonlinear system of parabolic partial differential equations of second order(see[22]),the Ricci flow in many respects appears to be very natural equation.

Note that most of the contributions from geometric analysis to date have involved either elliptic or parabolic equation.The elliptic and parabolic partial differential equations have been successfully applied to differential geometry and physics.A natural and important question is whether the well-developed theory of hyperbolic differential equations may be applied to solve problems in differential geometry and theoretical physics.In geometry,a good example is the singularity developed in general relativity,but the major problem here is that one has very little understanding of the global behavior of nonlinear hyperbolic systems when the spatial dimension is greater than one(see[19]).In fact,there are plenty of existing problems that involve hyperbolic equations.To this end,Kong and Liu[14]introduced a new flow called hyperbolic geometric flow(HGF,for short)in 2007.HGF is helpful to understand the wave character of the metrics,wave phenomenon of the curvatures,the evolution of manifolds and their structures(see[8,13–14,17,23]).

It is generally known that HGF equation is quite diffcult to solve in all generality unlike the nonlinear elliptic problems with a well-developed regularity theory.Although the short time existence of solutions is guaranteed by hyperbolic nature of the equations,their(long time)convergence to canonical geometric structures is analyzed under various conditions.For some recent work and the related results in this direction,see[7,10–11,15–16,23].

In[8],the authors studied the local forms of the evolutions under the HGF.They proved the following result.

Theorem 1.1(see[8])Assume that(M,g(t)),t∈[0,T)is a family of complete Rie-mannian manifolds evolving under hyperbolic geometric flowthe curvaturetensors satisfy the evolution equations

where all those components of metric,curvatures,etc.are components with respect to a local normal coordinate system around a fixed point p∈M,Bijkl=gprgqsRpiqjRrksl,andΔis the Laplacian with respect to the evolving metric g(t).

Here “Ric” and “Scal” denote the Ricci and scalar curvatures of(M,g(t)),respectively.Analogous results for the Einstein’s hyperbolic geometric flow(2.3)and the dissipative hyperbolic geometric flow(2.4)occur in[7,10],respectively.

The purpose of this paper is to derive the global forms of evolution equations for Riemannian,Ricci and scalar curvatures under HGF.Motivated by the techniques and ideas concerning the Ricci flow in Brendle’s paper[3–4],we give and prove the following main results.

Theorem 1.2Let X,Y,Z,W be fixed vector fields on M.Then under the HGF(2.1),we have

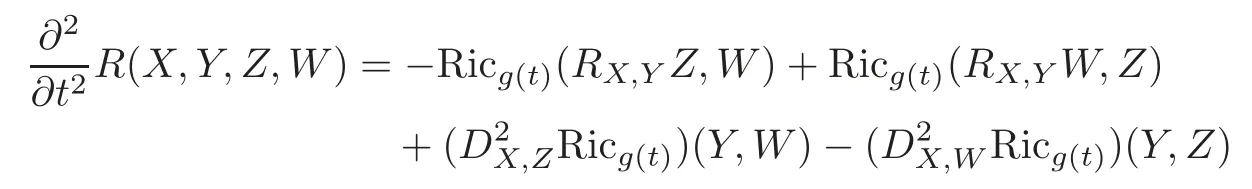
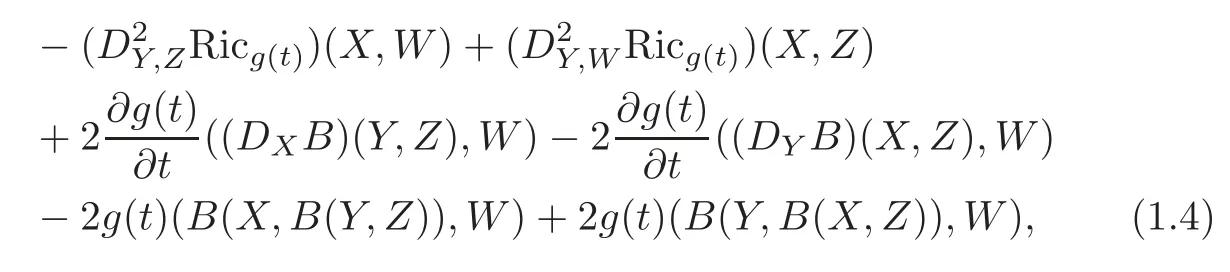
where B(X,Y):=(DXY),and the alternative notation R(X,Y)Z for RX,YZ is convenient.

Theorem 1.3Let X,Y,Z,W be arbitrary vector fields on M.Then under the HGF(2.1),the curvature tensors satisfy the evolution equations

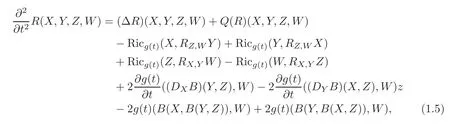
where Q(R):=R2+R#is a curvature tensor satisfying the first Bianchi identity,and with respect to a given local orthonormal basis{e1,···,en},R2and R#are defined by

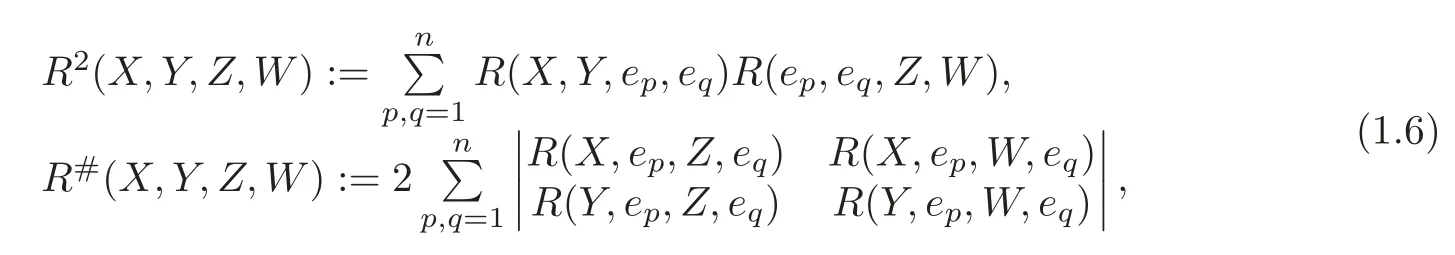
respectively.

Theorem 1.4Let X,Y be arbitrary vector fields on M.Then under the HGF(2.1),the Ricci curvature tensorRicg(t)and scalar curvatureScalg(t)satisfy the evolution equations,respectively,

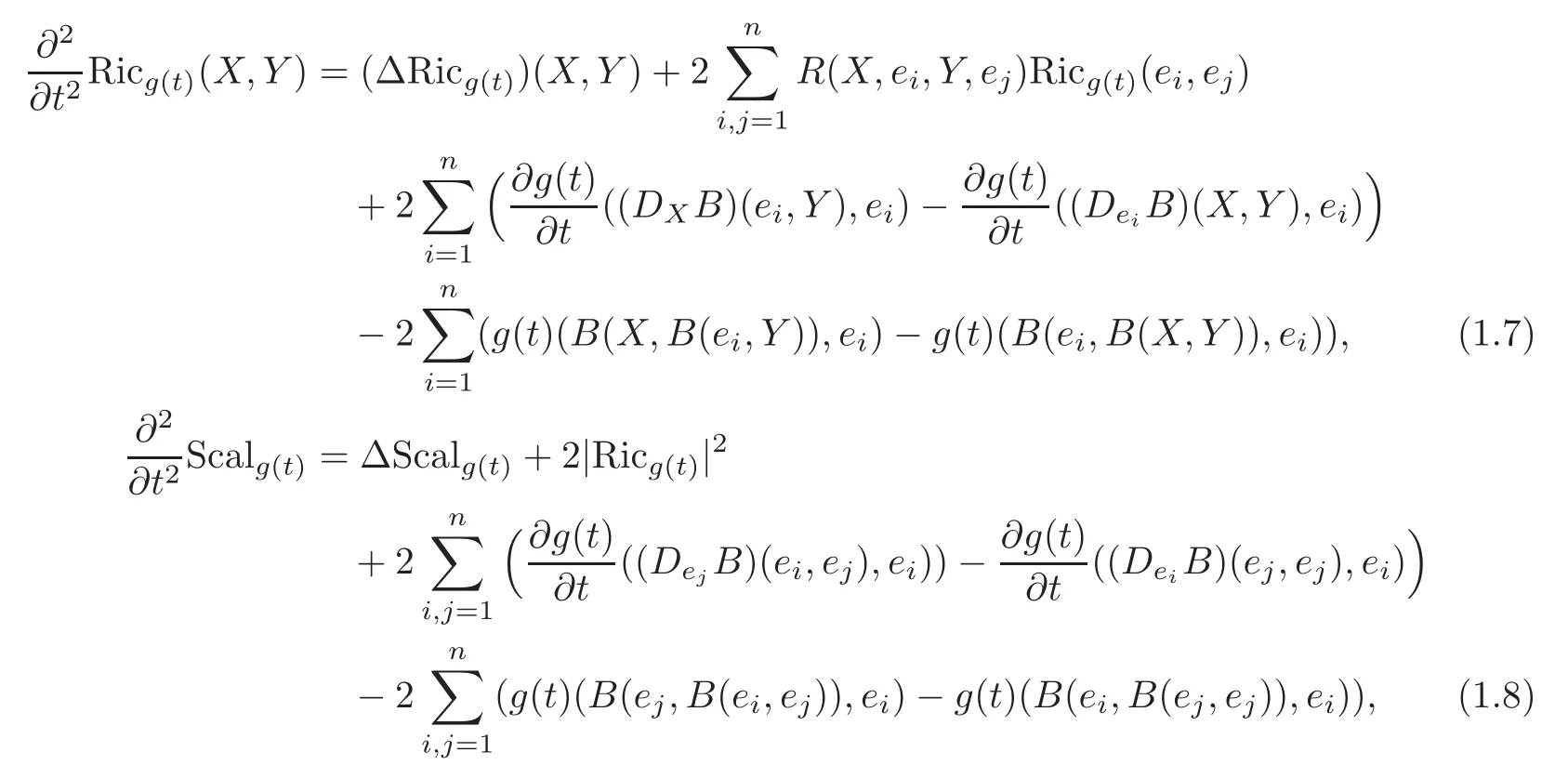
where{e1,···,en}is a local orthonormal basis of M,and(Ric(ei,ej))2.

On the other hand,hyperbolic differential equations model things like wave or vibrations,which may never reach equilibrium.These equations are more prone to singularities than parabolic ones(see[24]).Based on Theorem 14.1 in[9]which states that a maximal solution to the Ricci flow that develops a singularity in finite time must have unbounded curvature,we conjecture that there is a corresponding conclusion in the HGF case,see Theorem 4.1.

The structure of the paper is as follows.In Section 2,we state the related concepts and present some examples of specific solutions to the HGF.In Section 3,we give evolution equations for the Levi-Civita connection and prove the main results in the introduction.In Section 4,we consider Ricci curvature blow-up at finite-time singularities.Section 5 presents some problems for further study.

2 The Hyperbolic Geometric Flow

The hyperbolic geometric flow(HGF,for short)differs from the Hamilton’s Ricci flow,although these two flows share a common Ricci term?2Ricg(t).Its definition is as follows.

Definition 2.1(see[14])Let M be a manifold.The hyperbolic geometric flow is the evolution equation

for a one-parameter family of Riemannian metrics g(t),t∈[0,T)on M.We say that g(t)is a solution to the hyperbolic geometric flow if it satisfies(2.1).

Similarly to the Ricci flowthe HGF equation(2.1)is an unnormalized evolution equation.In[14],Kong and Liu also considered the normalized version of hyperbolic geometric flow,which preserves the volume of the flow.Considering the HGF and the normalized HGF differ only by a change of scale in spaceMand a change of timet.The normalized HGF equation takes the form

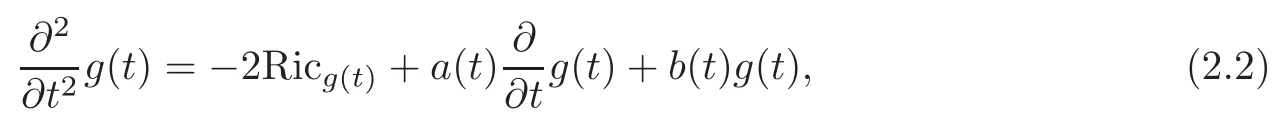
wherea(t)andb(t)are certain functions oft.

In order to further understand the relationship between the Einstein equation and the HGF,Kong and Liu also introduced the so-called Einstein’s hyperbolic geometric flow.

Definition 2.2(see[7])LetR×M be a space-time with the Lorentzian metricds2=dt2+gij(x,t)dxidxj.Suppose that the Einstein equations in the vacuum,which correspond to the metricds2,have the form

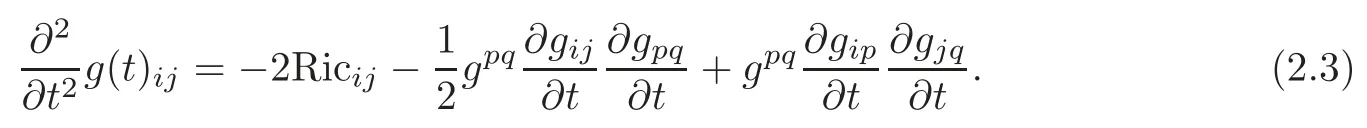
The equation(2.3)is called the Einstein’s hyperbolic geometric flow.

Motivated by the well-developed theory of the dissipative hyperbolic equations,the paper[7]introduced a new geometric analytical tool called dissipative hyperbolic geometric flow defined by

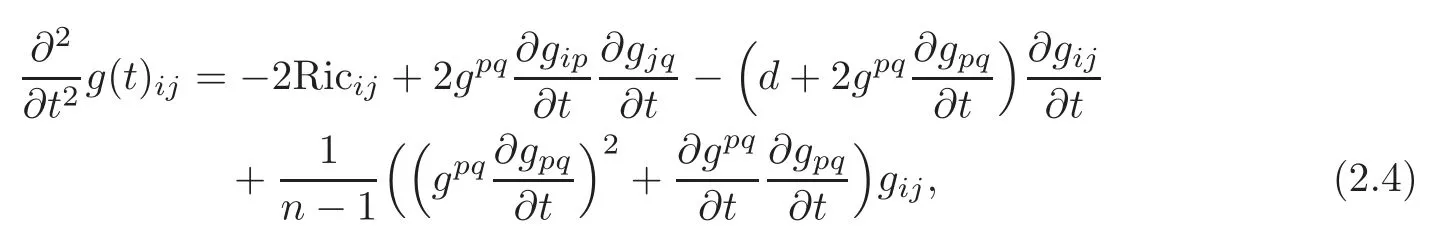
wheredis a positive constant.The reason that(2.4)is chosen as the equation form of dissipative hyperbolic geometric flow is that,in the case it possesses a simpler equation satisfied by the scalar curvature.

Next we describe some examples of specific solutions(see[7–8,10,14–15])so that we may get a better sense of the HGF.

Example 2.1(i)(Trivial example)If the initial metric is Ricci flat,so that Ricij=0,then clearly the metric does not change under(2.1).Hence any Ricci flat metricg(t)is a stationary solution to the HGF.This happens,for example,on the flat torus or on any K3-surface with a Calabi-Yau metric.

(ii)(Non-trivial example)A typical example of the Einstein metric is

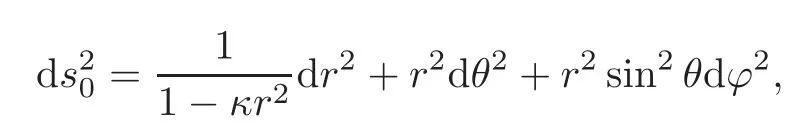
whereκis a constant taking its value?1,0 or 1.We can prove that the metric

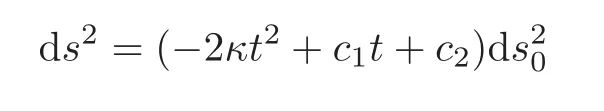
is a solution to the HGF(2.1),wherec1andc2are two constants.

Example 2.2Consider a solution in conformal class with the following form:

Suppose that the initial metricgij(0,x)is Einstein,that is,there exists some constantλsuch that

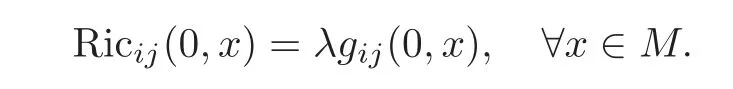
Then(2.5)withρ(t)=?λt2+vt+1 and a real numbervstanding for the initial velocity,is a solution to the equation(2.1).

3 Evolution Equations and Proofs of the Main Results

In this section,we use the techniques of Brendle[3–4]in studying evolution equations along the Ricci flow to derive evolution equations with global forms along the HGF.

From now on,we assume that(M,g(t)),t∈[0,T),is a family of complete Riemannian manifolds evolving under HGF.

3.1 Evolution of the Levi-Civita connection

LetX,Ybe fixed vector fields onM(that is,X,Yare independent oft).We define

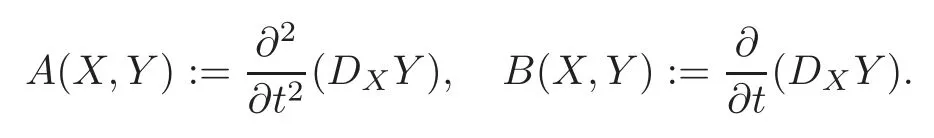
Observe that the difference of two connections is always a tensor,consequently,A,Bare tensors.

Proposition 3.1Let X,Y,Z be fixed vector fields on M.Then

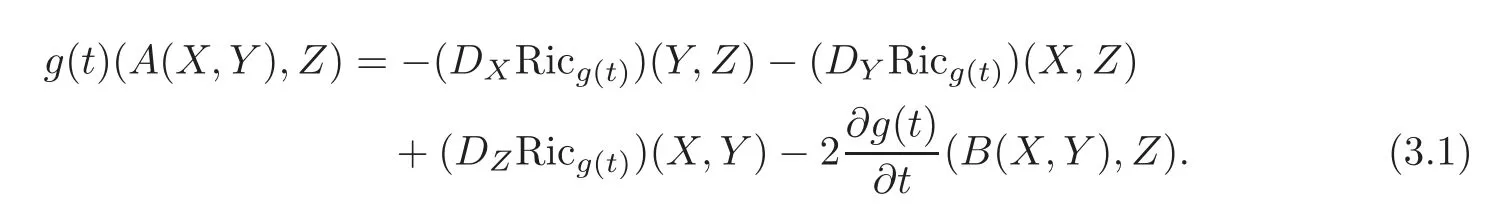
ProofDifferentiatingg(t)(DXY,Z)twice with respect tot,we have

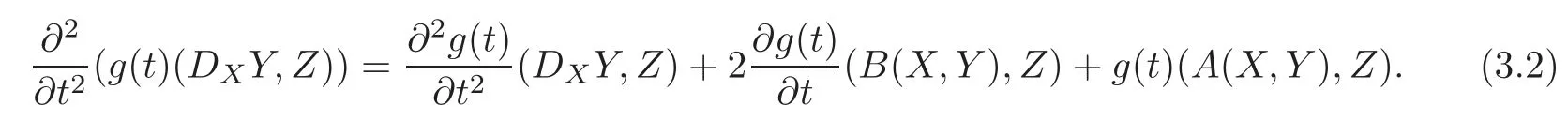
Since the Levi-Civita connection satisfies

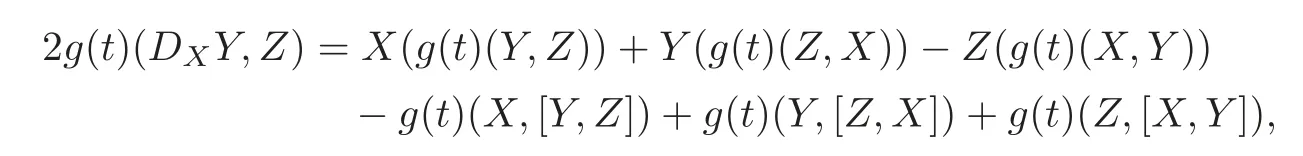
(3.2)can be rewritten in the following form:

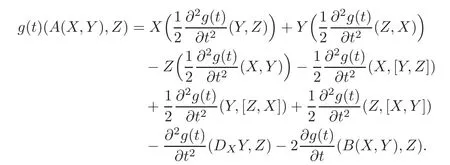
By the definition of HGF,we have

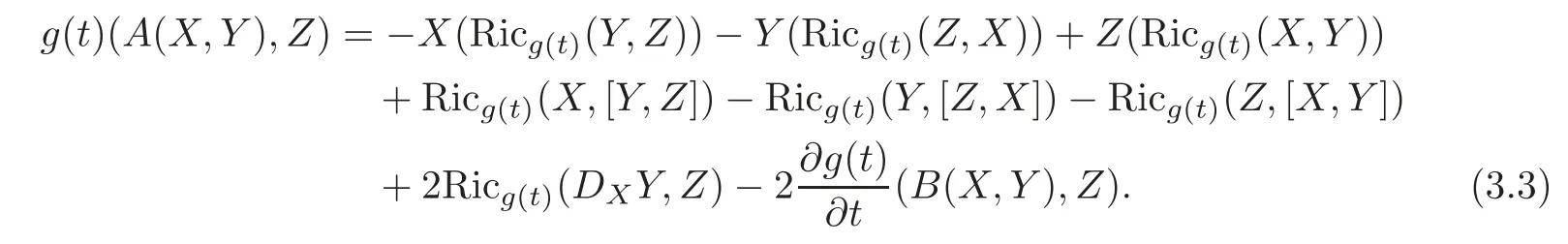
Noting thatAis a tensor,we conclude that

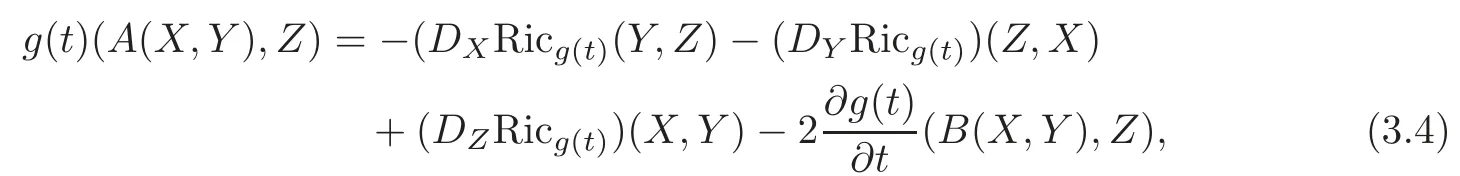
as claimed.

3.2 Proof of Theorem 1.2

Now we return to compute the evolution equation for the curvature tensor.For convenience we need the second order covariant derivativeD2X,YZdefined by

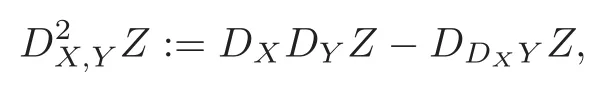
from which we have

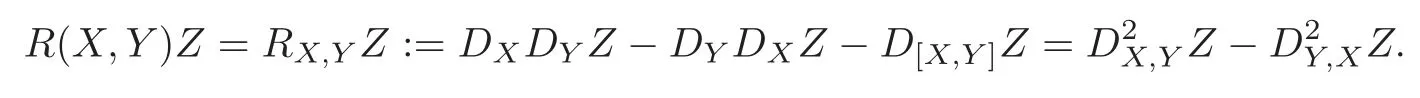
Proof of Theorem 1.2The second derivative ofRX,YZyields

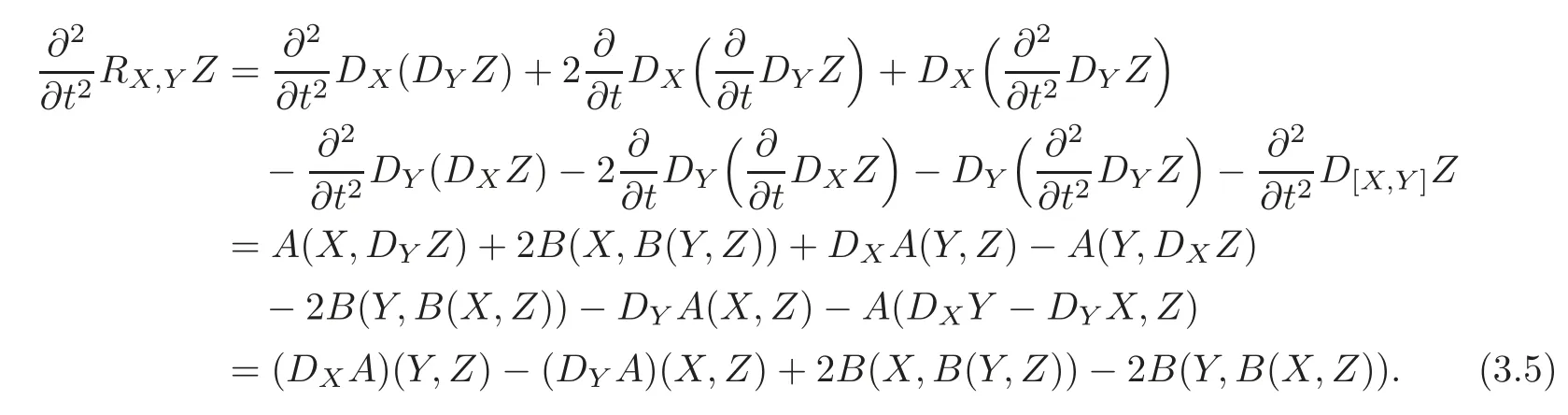
This implies

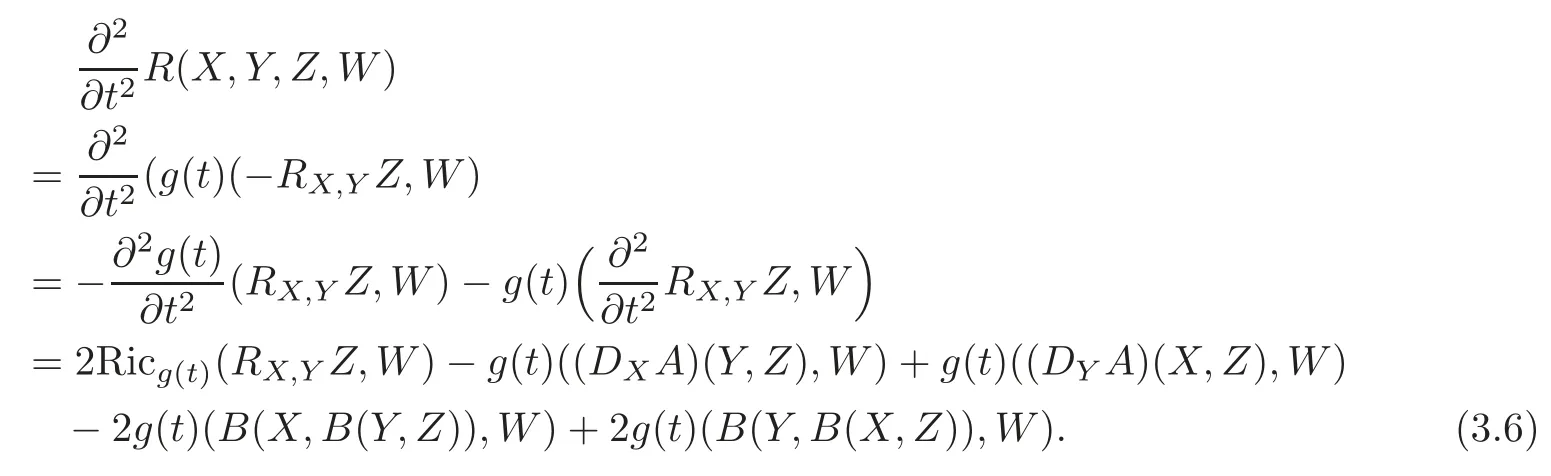
Applying Proposition 3.1,we obtain

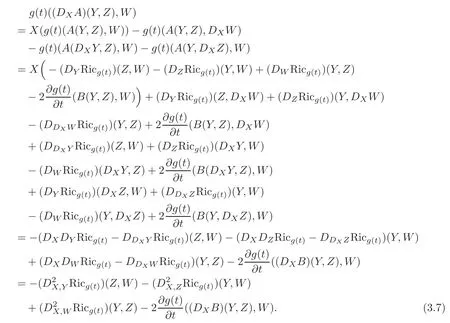
Interchanging the roles ofXandYyields

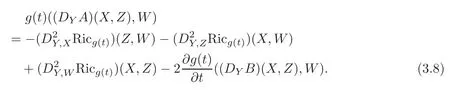
Moreover,we have

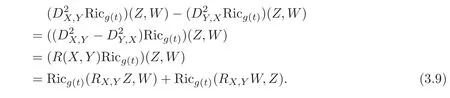
Substituting(3.7)–(3.9)into(3.6)yields

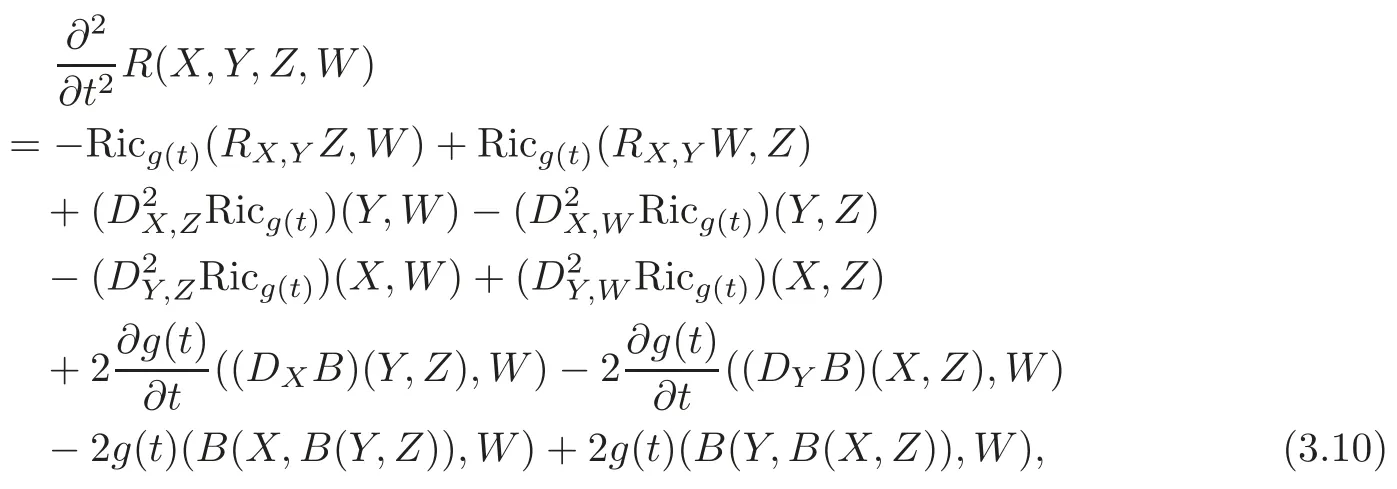
as claimed.

3.3 Proof of Theorem 1.3

We will show that we can rewrite the right-hand side of(3.10)so that the Laplacian of the curvature tensor term will appear up to lower order terms.To this end,we first give the following lemma which is independent of any evolution.

Lemma 3.1(see[3])Let X,Y,Z,W be arbitrary vector fields on M.Then

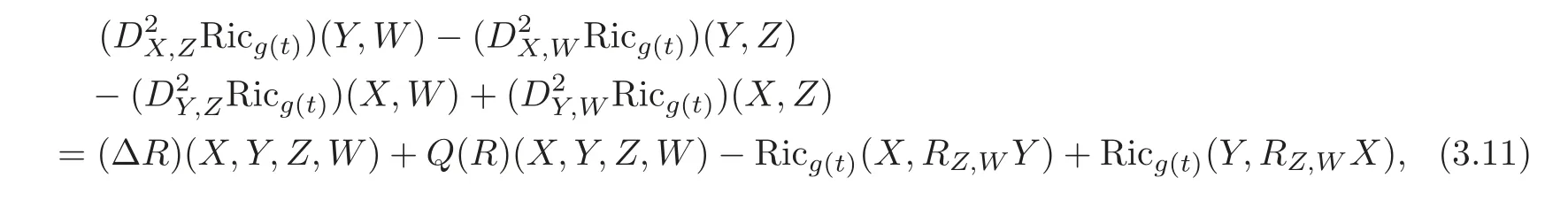
where Q(R):=R2+R#is a curvature tensor satisfying the first Bianchi identity,and with respect to a local orthonormal basis{e1,···,en},R2and R#are dif i ned by(1.6)in Theorem1.3.

ProofUnder an orthonormal basis{e1,···,en},it is easy to show that

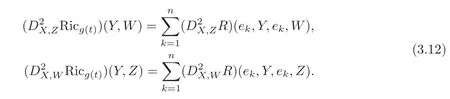
Using the second Bianchi identity,after a direct computation,we obtain

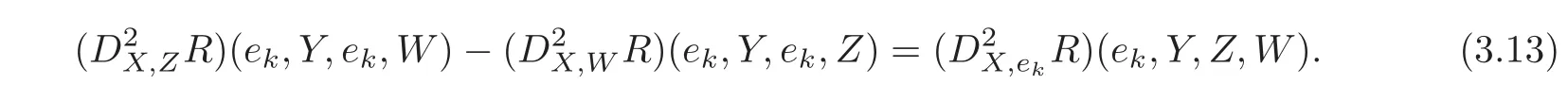
Thus we have

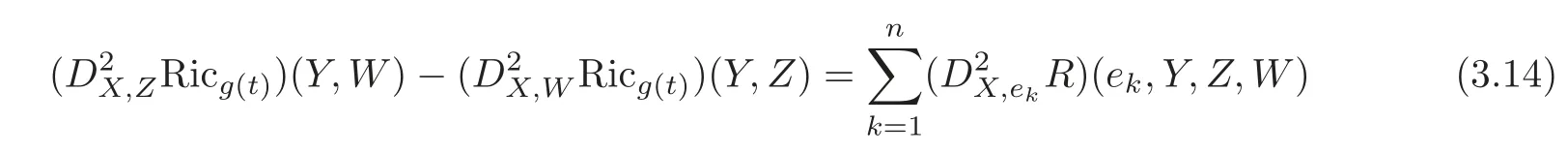
and

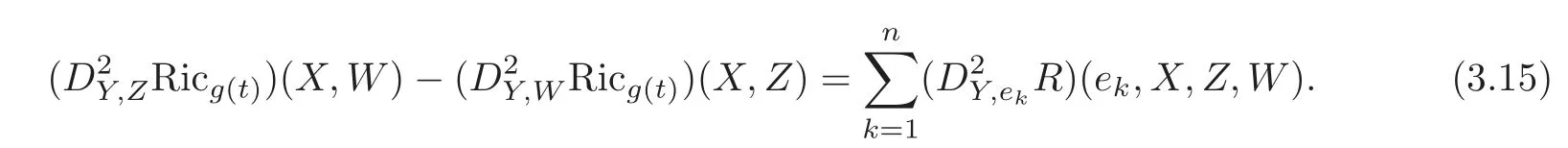
Therefore,(3.14)–(3.15)imply

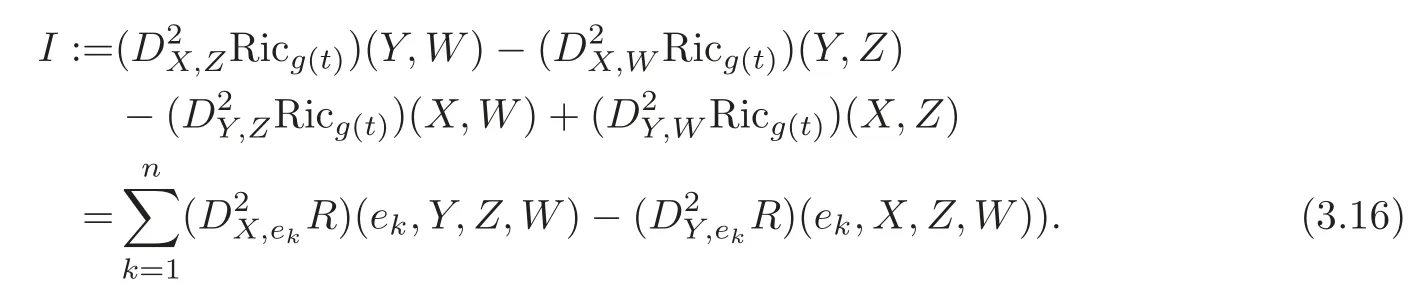
Now we consider to putQ(R)into(3.16).Note that

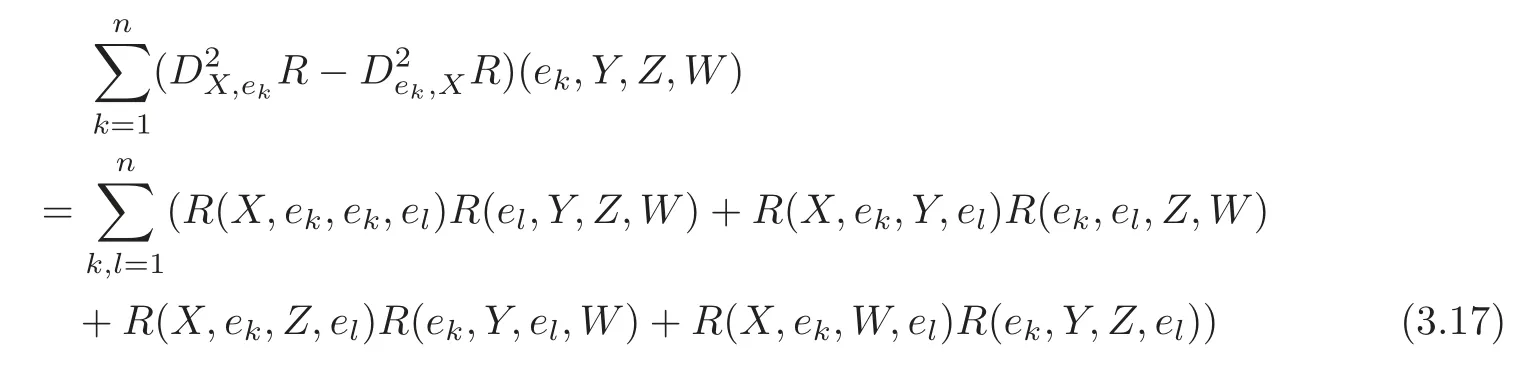
and

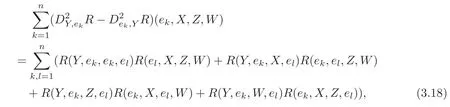
we have

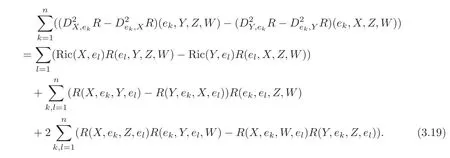
By definitions ofR2andR#,together with the first Bianchi identity

(3.19)can be reduced as

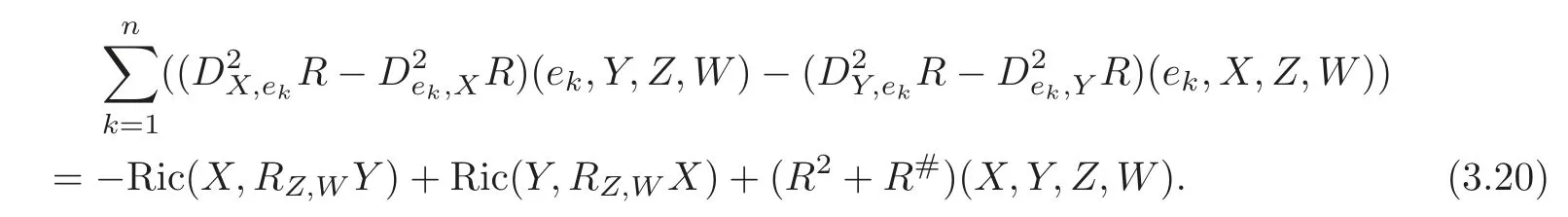
Hence,from(3.16)and(3.20)we have

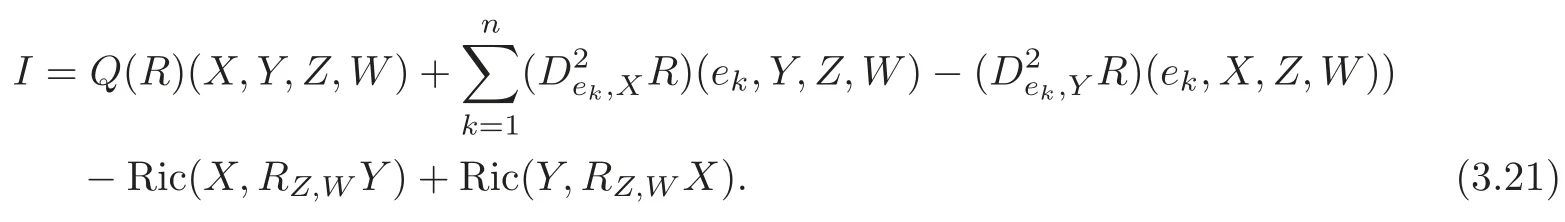
Next we consider to put ΔRinto(3.20).Similarly to(3.13),we have

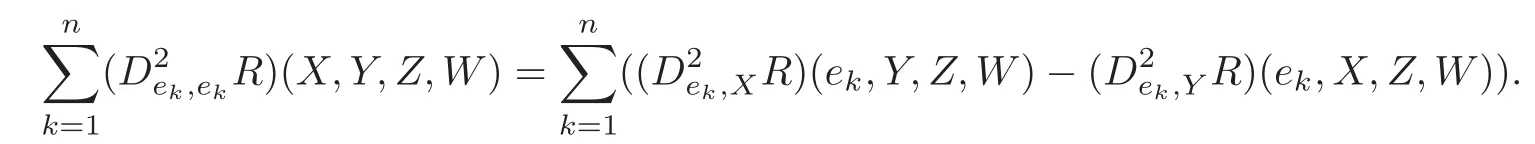
Moreover,recall that

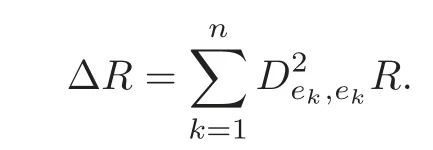
After putting these facts together,the desired equation(3.11)follows immediately.

Proof of Theorem 1.3By Theorem 1.2 and Lemma 3.1,we obtain the following wave equation for curvature tensor:

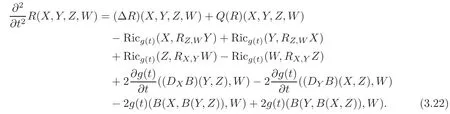
3.4 Proof of Theorem 1.4

Recall that the HGF is an evolution equation on the metricgij(t).The evolution for the metric implies a nonlinear wave equation not only for the Riemannian curvature tensor,but also for the Ricci curvature tensor and the scalar curvature.This result(Theorems 1.4)is stated in the introduction.Now we give its proof.

Proof of Theorem 1.4Similarly to(3.12),we have

By the definition ofQ(R),we have

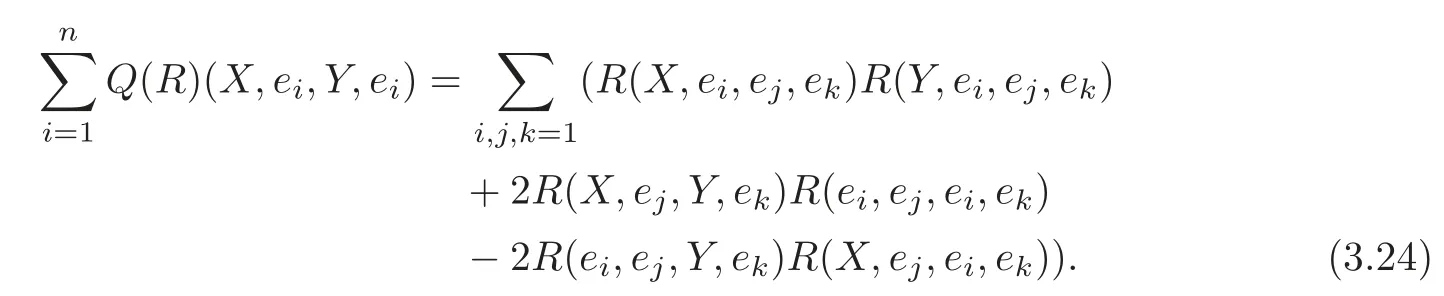
Using the first Bianchi identity,we obtain

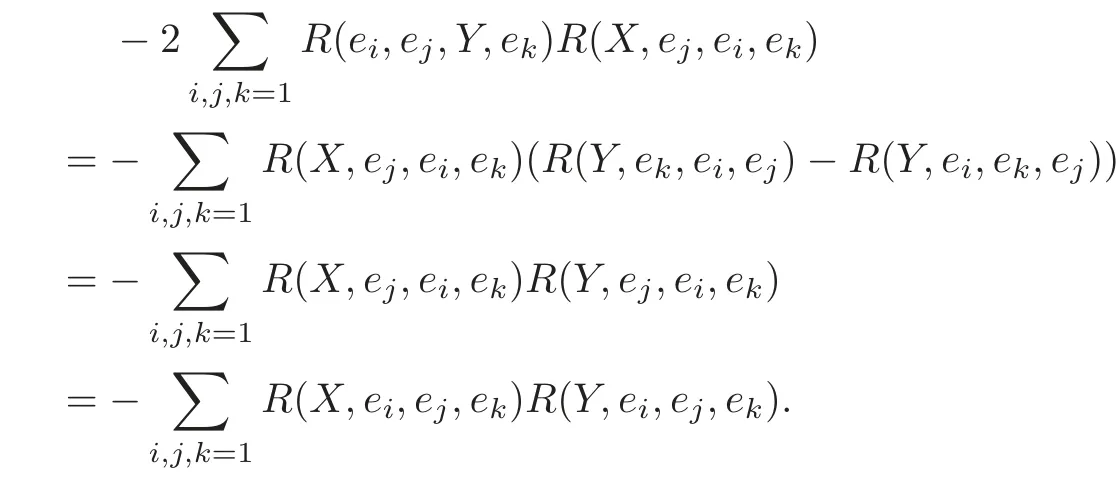
Hence(3.24)can be reduced as

Moreover,we have

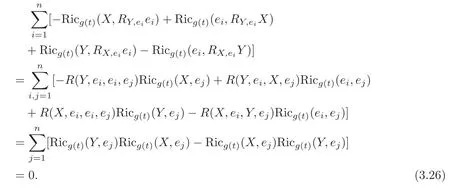
Using Theorem 1.3,or by(3.22),together with(3.23),(3.25)–(3.26),we get

which is the first claimed equation(1.7).

As for the second assertion(1.8),noting that

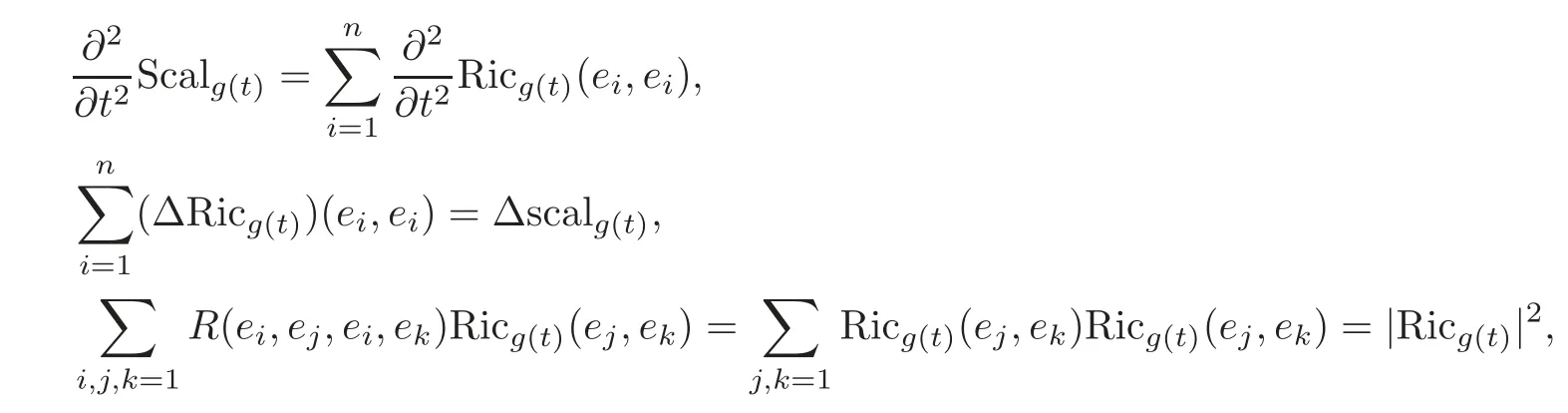
it follows from(3.27)that

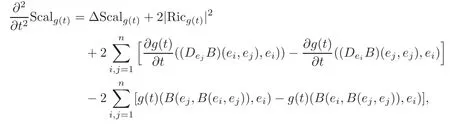
as claimed.

4 Curvature Blow-up at Finite-Time Singularities

In this section,we consider a maximal solution to the HGF which is defined on a finite interval[0,T).Similarly to the result in Hamilton’s paper(see[9,Theorem 14.1]),we show that such a solution must have unbounded curvature.Our proof is inspired in part by the proof of Theorem 6.1 in[23]and is greatly improved.

Theorem 4.1Let M be a compact manifold,and let g(t),t∈[0,T),be a maximal solution to the HGF(2.1)on M.Moreover,suppose that T＜∞.Then

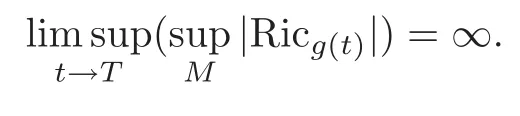
ProofWe argue by contradiction.Assuming that the Ricci tensor ofg(t)is uniformly bounded for allt∈[0,T),that is,there exists a positive constantm0such that|Ricg(t)|≤m0,t∈[0,T).So the solutiong(t)can be extended to a larger time interval[0,T+ε),whereεis a positive real number.Indeed,by(2.1),we have the relations

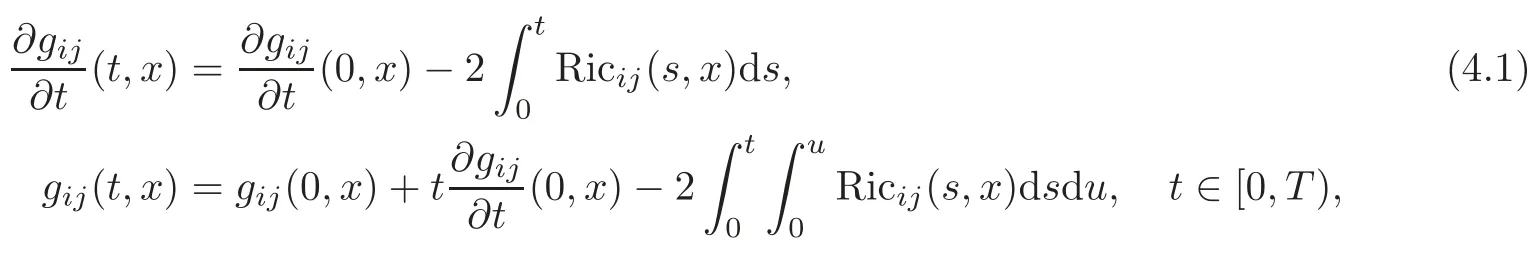
which imply

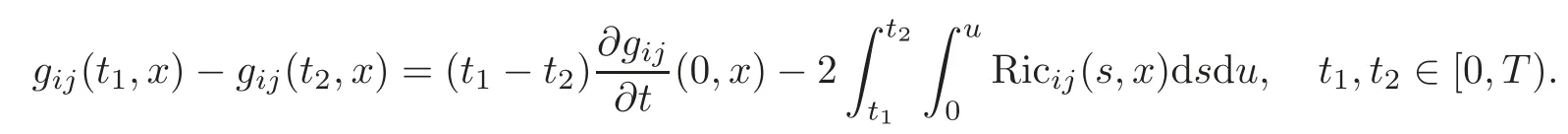
Hence we obtain

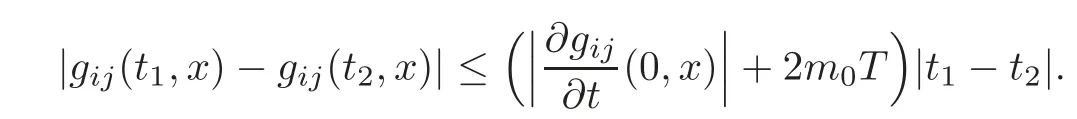
Therefore for any suffciently small numberε＞0,there existssuch that as|t1?t2|＜δ,always holds

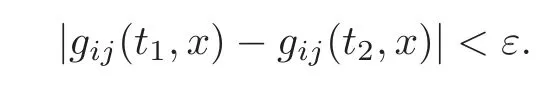
By the Cauchy Criterion,exists for alli,j,which implies thatexists.Sinceexists(see Definition 2.1),together with(4.1),we have thatandConsequently,g(t):=g(t,x),t∈[0,T]is the solution to a HGF.

In this case,g(t)may be extended from being aC∞solution on[0,T)to aC∞solution on[0,T].Then we takeg(T),to be an initial metric by a short-time existence theorem(see[14,Theorem 1])in order to extend the solution to a HGF fort∈[0,T+ε).This contradicts the assumption that[0,T)is a maximal time interval.Therefore,we complete the proof.

5 Some Problems for Further Study

To conclude this paper,we raise two questions for a future study.Since we have the global forms of evolution equations(1.4)–(1.5),(1.7)–(1.8)along the HGF(2.1),in the future we are interested in the following problems:

1.For fixed(t,p)∈[0,T]×M,we denote byKmax(t,p)/Kmin(t,p)the maximum/minimum sectional curvature ofg(t)at the pointp.Moreover,for abbreviation,we define

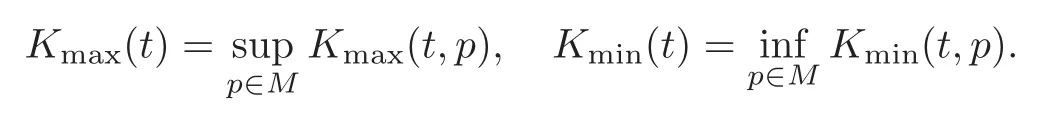
Let{tk}be a sequence of times such thatfor allk.Then by Theorem 4.1,does the following relation hold:

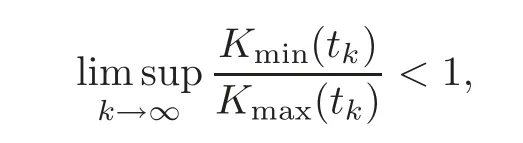
or

2.(Preserved curvature conditions by the HGF)We know that if we want to study the global properties of HGF,then it is important to find curvature conditions that are preserved under the evolution.How to develop such techniques?For instance,suppose thatMis a compact manifold,and letg(t),t∈[0,T)be a solution to HGF onM,and consider an appropriate ODE(?)+(certain term).Can we claim that the nonnegative isotropic curvature(see[3])is preserved by the ODE(?)?

AcknowledgementThe author thanks Professor Kefeng Liu for offering him tremendous information and constructive suggestions.He would like to thank Professor Hongwei Xu for a helpful discussion on a course based Brendle’s book Ricci Flow and the Sphere Theorem.

[1]Brendle,S.,Convergence of the Yamabe flow for arbitrary initial energy,J.Differential Geom.,69,2005,217–278.

[2]Brendle,S.,Convergence of the Yamabe flow in dimension 6 and higher,Invent.Math.,170,2007,541–576.

[3]Brendle,S.,Ricci flow and the sphere theorem,Grad.Studies in Math.,111,AMS.,Providence RI,2010.

[4]Brendle,S.and Schoen,R.,Manifolds with-pinched curvature are space forms,J.Amer.Math.Sco.,200,2009,1–13.

[5]Chow,B.,The Yamabe fow on locally conformally flat manifolds with positive Ricci curvature,Comm.Pure Appl.Math.,65,1992,1003–1014.

[6]Chow,B.,Lu,P.and Ni,L.,Harmilton’s Ricci Flow,American Mathematical Society and Science Press,Lectures in Contemp.Math.3,AMS,Providence RI,2006.

[7]Dai,W.R.,Kong,D.X.and Liu,K.F.,Dissipative hyperbolic geometric flow,Asia J.Math.,12,2008,345–364.

[8]Dai,W.R.,Kong,D.X.and Liu,K.F.,Hyperbolic geometric flow(I):short-time existence and nonlinear stability,Pure and Applied Mathematics Quarterly,6(2),2010,331–359(Special Issue:In honor of Michael Atiyah and Isadore Singer).

[9]Hamilton,R.,Three-manifolds with positive Ricci curvature,J.Differential Geom.,17,1982,255–306.

[10]He,C.L.,Exact solutions for Einstein’s hyperbolic geometric flow,Communications in Theoretical Physics,50,2008,1331–1553.

[11]Hiric?,I.E.and Udriste,C.,Basic evolution PDEs in Riemannian geometry,Balkan Journal of Geometry and Its Applications,17(1),2012,30–40.

[12]Jost,J.,Riemannian Geometry and Geometric Analysis,6th ed.,Springer-Verlag,Berlin,2011.

[13]Kong,D.X.,Hyperbolic geometric flow,The Proceedings of ICCM 2007,Vol.II,Higher Educationial Press,Beijing,2007,95–110.

[14]Kong,D.X.and Liu,K.F.,Wave character of metrics and hyperbolic geometric flow,J.Math.Phys.,48,2007,103508-1–103508-14.

[15]Kong,D.X.,Liu,K.F.and Wang,Y.Z.,Life-span of classical solutions to hyperbolic geometric flow in two space variables with slow decay initial data,Communications in Partial Differential Equations,36,2011,162–184.

[16]Kong,D.X.,Liu,K.F.and Xu,D.L.,The hyperbolic geometric flow on Riemann surfaces,Communications in Partial Differntial Equations,34,2009,553–580.

[17]Liu,K.F.,Hyperbolic geometric flow,Lecture at International Conference of Elliptic and Parabolic Differential Equations,Hangzhou,2007.Available at preprint webpage of Center of Mathematical Science,Zhejiang University.

[18]Milgram,A.and Rosenblum,P.,Harmonic forms and heat conduction,I:Closed Riemannian manifolds,Proc.Nat.Acad.Sci.,37,1951,180–184.

[19]Schoen,R.and Yau,S.T.,Lectures on Differential Geometry,International Press,Boston,1994.

[20]Schwetlick,H.and Struwe,M.,Convergence of the Yamabe flow for “l(fā)arge” energies,J.Reine Angew.Math.,562,2003,59–100.

[21]Topping,P.,Lectures on the Ricci Flow,LMS Lecture Notes,325,London Math.Society Lecture Note Series,325,Cambridge University Press,Cambridge,2006.

[22]Turk,D.,Deforming metrics in the derection of their Ricci tensors,J.Diffrential Geom.,18,1983,157–162.

[23]Udri?ste,C.,Riemann flow and Riemann wave via bialternate productRiemannian metric,arXiv:1112.4279v1

[24]Yau,S.T.and Nadis,S.,The shape of inner space:String theory and the geometry of the universes hidden dimensions,Basic Books,A Member of the Perseus Books Group,New York,2010.

[25]Ye,R.,Global existence and convergence of Yamabe flow,J.Differential Geom.,39,1994,35–50.

[26]Zhu,X.P.,Lectures on mean curvature flows,Studies in Advanced Mathematics,32,AMS/IP,Providence RI/Somerville,MA,2002.