Fei JIANG Song JIANG Weiwei WANG

1 Introduction

We consider the two-phase free boundary problem for the equations of two incompressible immiscible fluids within the infinite slab Ω =R2×(?1,1)?R3and for timet≥0.The fl uids are separated by a moving free interface Σ(t)which is given by the unknown functionη:R+×R2→R.Hence we can define Σ(t):={x∈R3|x3=η(t,x′)}for eacht≥0,wherex′=(x1,x2)T,and the superscript T means matrix transposition.

The interface divides Ω into two time-dependent disjoint open subsets Ω±(t),so that Ω =Ω+(t)∪Ω?(t)∪Σ(t)andThe motion of the fluids is driven by the constant gravitational field alonge3,i.e.,thex3direction,andG=(0,0,?g)Twithg＞0.

The two fluids are described by their velocity and pressure functions,which are given,for eacht≥0,by

respectively.We assume that at a given timet≥0,these functions have well-defined traces onto Σ(t).

The fluids under consideration are incompressible and viscous.Hence,fort＞0,the fluids satisfy the following equations of motions:

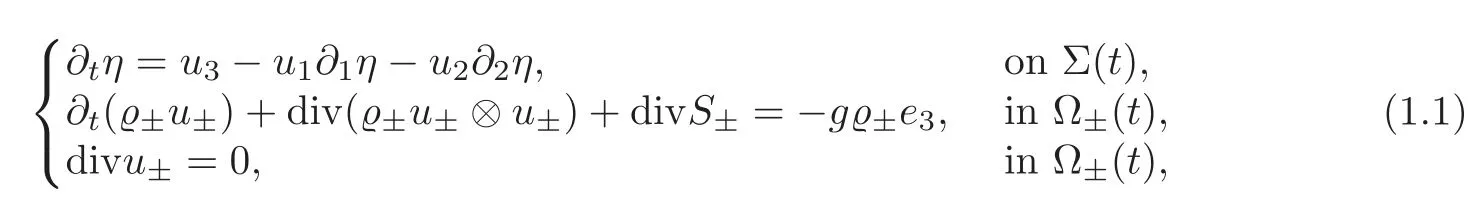
where the first equation of(1.1)describes the motion of the free interface(see[7,17]),?i:=?xi,and the positive constants?±denote the densities of the respective fluids,and we define the stress tensor by

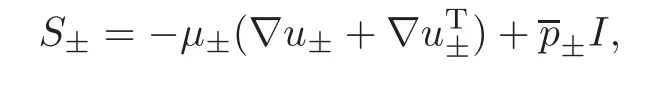
withμ±andp±being the viscosity coeffcient and the pressure of the respective fluids,andIthe 3×3 identity matrix.

For two viscous fluids meeting at a free boundary with surface tension,from the physical point of view,the velocity is continuous across the interface,and the jump in the normal stress is proportional to the mean curvature of the surface multiplied by the normal to the surface(see[2,24]).Thus,we impose the jump conditions at the free interface as follows:

where the interfacial jump is defined by

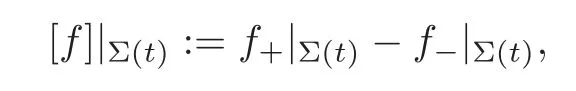
f|Σ(t)is the trace of a quantityfon Σ(t),and

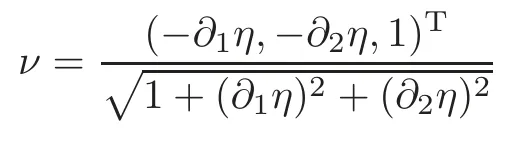
denotes the normal vector to the free surface Σ(t).The jump condition of(1.2)implies that there is no possibility for the fluid to slip past each other along Σ(t).Here we takeHto be twice the mean curvature of the surface Σ(t)and the surface tension to be a constantκ≥0.Since Σ(t)is parameterized by(x′,η(t,x′)),we may employ the standard formula for the mean curvature of a parameterized surface to write

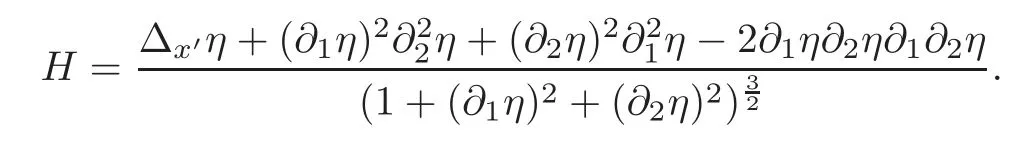
We also enforce the condition that the normal component of the fluid velocity vanishes at the fixed boundaries,that is,

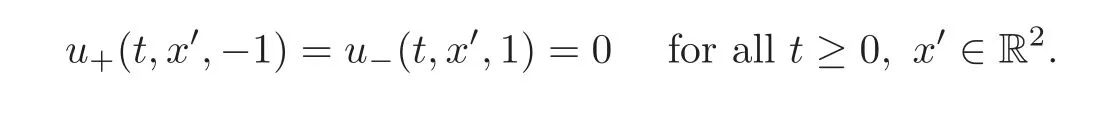
To complete the statement of the problem,we have to specify initial conditions.We give the initial interface Σ(0)= Σ0,which yields the open sets Ω±(0)on which we specify the initial data for the velocity and height of interface

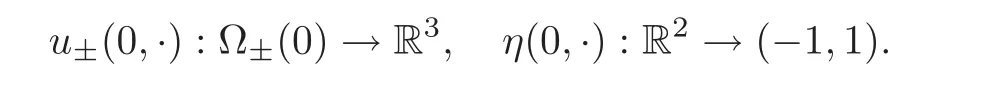
Thus the initial datum of the pressure can be given by?±,η(0,·)andu±(0,·).To simplify the equations,we introduce the indicator functionsχΩ±,denote

and define the modified pressure by

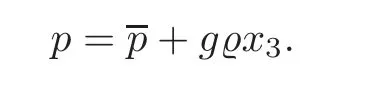
Thus,for eacht＞0,(1.1)can be rewritten as

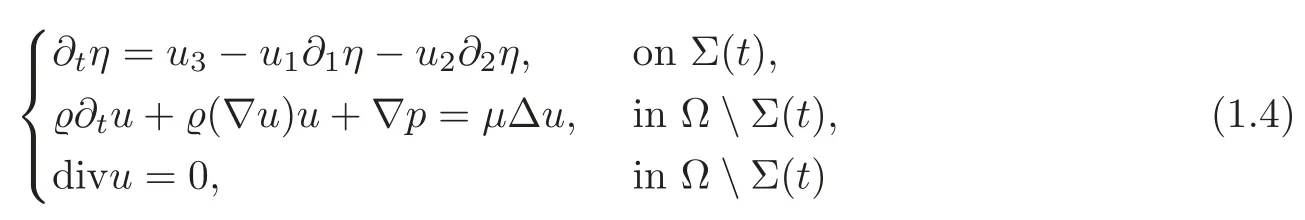
and the jump condition(1.3)becomes,setting[?]=?+???,

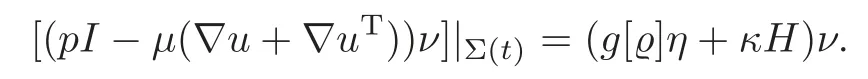
For convenience in subsequent analysis,we will use the notation

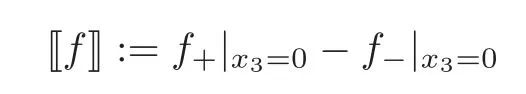
for the jump of a quantityfacross the set{x3=0}.

Now,we linearize(1.4)around a steady-state solutionη=0,u=0 andp=constant,and then the resulting linearized equations read as

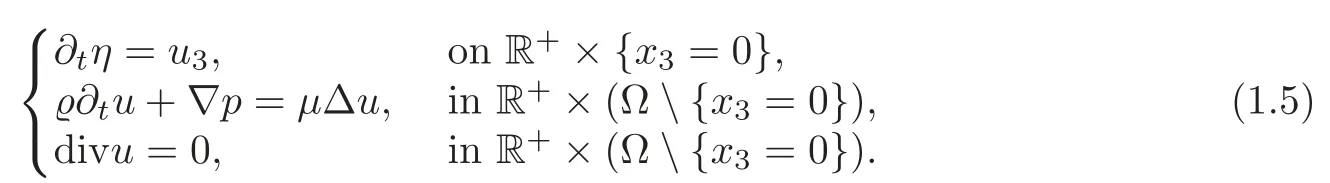
The corresponding linearized jump conditions are

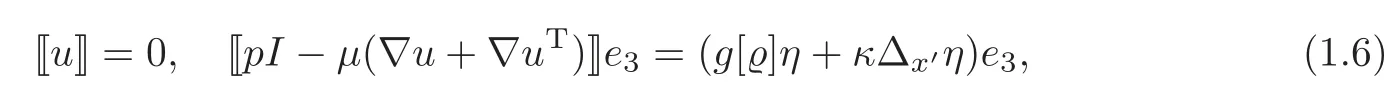
while the boundary conditions are

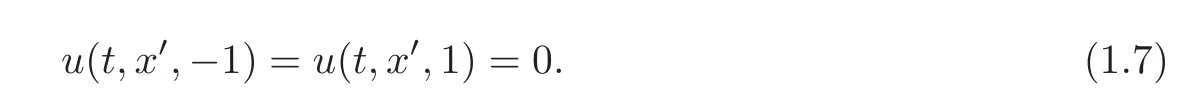
We consider two completely plane-parallel layers of immiscible fluid,the heavier on top of the light one and both subject to the earth’s gravity.In this case,the equilibrium state is unstable to sustain small perturbations or disturbances,and this unstable disturbance will grow and lead to a release of potential energy,as the heavier fluid moves down under the(effective)gravitational field,and the lighter one is displaced upwards.This phenomena was first studied by Rayleigh[18–19]and then Taylor[20],and therefore is called the Rayleigh-Taylor instability.In the last decades,many works related to this phenomena have appeared from both physical and numerical points of view.In particular,many results concerning linearized problems have been summarized in monographs(see,e.g.,[2,22]).To our best knowledge,however,there are only a few results of mathematical analysis on nonlinear problems in the literature,due to the fact that in general,the passage from a linearized instability to a dynamical nonlinear instability for a conservative nonlinear partial differential system is rather diffcult.In 1987,Ebin[4]proved the ill-posedness of the equations of motion for a perfect fluid with free boundary.Then,he adapted the approach of[4]to obtain the ill-posedness of both Rayleigh-Taylor and Helmholtz problems for two-dimensional incompressible,immiscible,inviscid fluids without surface tension(see[5]).In 2003,Hwang and Guo[10]showed the nonlinear Rayleigh-Taylor instability for two-dimensional,incompressible,inviscid fluids with continuous density,and their result was extended to magnetohydrodynamic(MHD)flows(see[9])recently.Unfortunately,the approaches in both[5]and[10]could not be applied to the viscous flow case,since the viscosity can bring some technical diffculties to the study of the nonlinear Rayleigh-Taylor instability.We should mention that Jiang et al.[11]showed the nonlinear RT instability offor the Cauchy problem of the nonhomogeneous incompressible viscous fluid with continuous density in the sense of Lipschitz structure recently.

In 2011,for two-compressible immiscible fluids evolving with a free interface(the density is discontinuous across the free interface),Guo and Tice made use of flow maps(Lagrangian coordinates)to transfer the free boundary into a fixed boundary and established a variational framework for nonlinear instability in[6],where with the help of the method of Fourier synthesis,they constructed solutions that grow arbitrarily quickly in time in the Sobolev space,leading to the ill-posedness of the perturbed problem in Lagrangian coordinates.It should be noted that they also investigated the stabilizing effect of viscosity and surface tension to the linear Rayleigh-Taylor instability(see[8]).However,the nonlinear instability for compressible flows still remains open.

In this paper,we will study the nonlinear Rayleigh-Taylor instability for two uniform viscous incompressible flows with surface tension and a free interface,across which the density is discontinuous.We will prove that in Eulerian coordinates,the corresponding linearized system is globally unstable in Sobolev spaces,and moreover,the original nonlinear problem with or without surface tension is globally unstable in an appropriate sense.For this purpose,we assume thatκ≥0 and that the upper fluid is heavier than the lower fluid,i.e.,

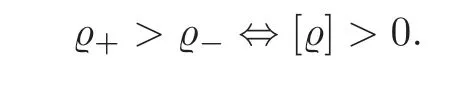
We mention that the analogue of the Rayleigh-Taylor instability arises when the fluids are electrically conducting and a magnetic field is present,and the growth of the instability will be inf l uenced by the magnetic field due to the generated electromagnetic induction and the Lorentz force(see[3,9,12–14,23]).Some authors have extended the partial results concerning the Rayleigh-Taylor instability of superposed flows to the case of MHD flows by overcoming additional diffculties induced by the presence of the magnetic field.

This paper is organized as follows.In Section 2,we state our results on the linearized system(1.5)and the nonlinear system(1.4),i.e.,Theorems 2.1–2.2.In Section 3,we construct the growing solutions to the linearized equations,while in Section 4,we analyze the linear problem and prove the uniqueness and Theorem 2.1.In Section 5,we prove the global instability of orderkof the nonlinear problem,i.e.,Theorem 2.2.

2 Main Results

Before stating the main results,we introduce the notation that will be used throughout the paper.For a functionf∈L2(Ω),we define the horizontal Fourier transform via

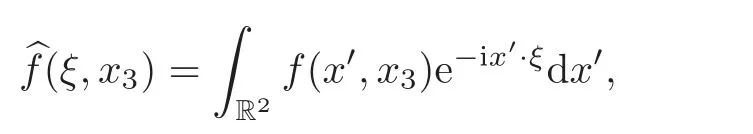
wherex′,ξ∈R2,and “·” denotes the scalar product.By the Fubini and Parseval theorems,we have

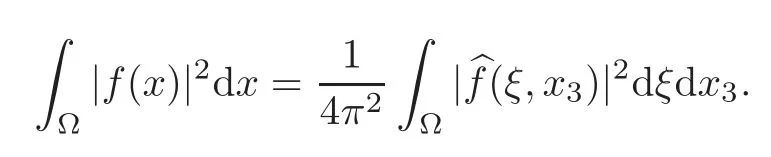
We now define a function space suitable for our analysis of two disjoint fluids.For a functionfdefined on Ω,we writef+for the restriction to Ω+=R2×(0,1)andf?for the restriction to Ω?=R2×(?1,0).Fors∈R,we define the piecewise Sobolev space of ordersby

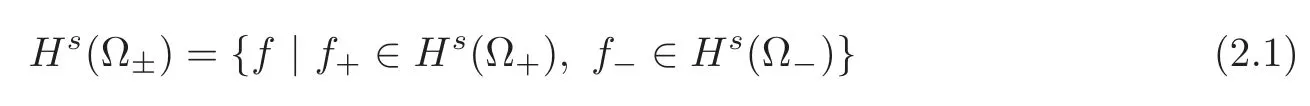
endowed with the norm

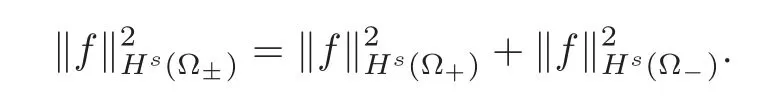
In a way similar to(2.1),for a functionfdefined on(0,∞)×Ω,for which an interface divides Ω into two time-dependent disjoint open subsets Ω±(t),so that Ω = Ω+(t)∪Ω?(t)∪Σ(t)andwe denote

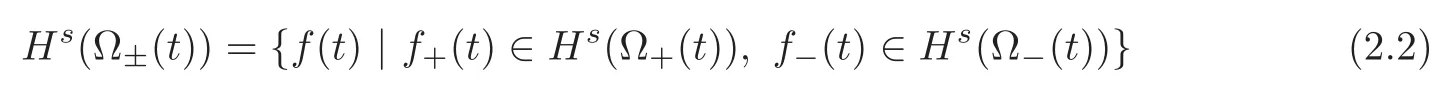
for eacht∈[0,∞).

In addition,fork∈N,we can take the norms to be given by

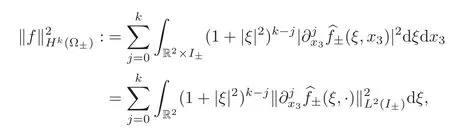
whereI?=(?1,0)andI+=(0,1).The main difference between the piecewise Sobolev spaceHs(Ω)and the usual Sobolev space lies in that we do not require functions in the piecewise Sobolev space to have weak derivatives across the set{x3=0}.Iff:=(f1,···,fn)T∈(Hs(Ω±))n,to shorten notation,we define

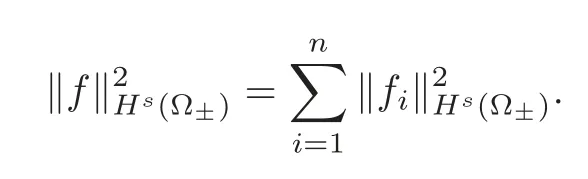
Now,we are in a position to state our first result,i.e.,the result of global instability for the linearized problem(1.5).

Theorem 2.1The linearized problem(1.5)with the corresponding jump and boundary conditions is globally unstable in the sense of Hadamard in Hk(Ω)for every k.More precisely,there exists a constant C1＞0,and for any k,j∈Nwith j≥k and for any α＞0,there existsa constant Cj,kdepending on j and k,and a sequence of solutionsto(1.5)satisfying the corresponding jump and boundary conditions(1.6)–(1.7),so that

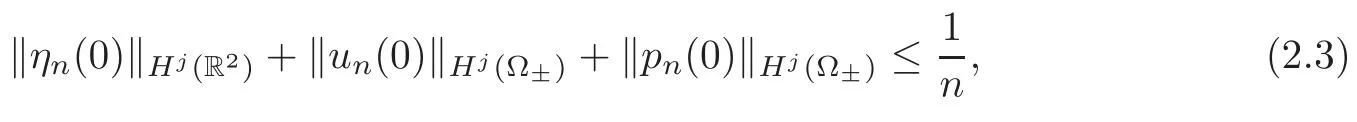
but

Moreover,

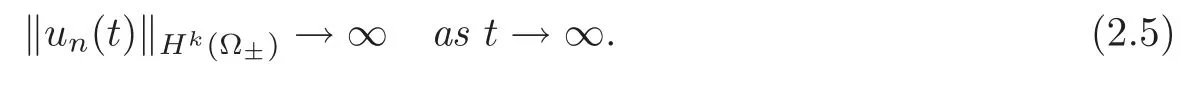
Theorem 2.1 shows globally discontinuous dependence of solutions upon initial data.The proof of Theorem 2.1 is inspired by[8]under necessary modifications and its basic idea is the following.First,we notice that the linearized equations have coeffcients that depend only on the vertical variablex3∈(?1,1).This allows us to seek “normal mode” solutions by taking the horizontal Fourier transform of the equations and assuming that the solutions grow exponentially in time by the factor eλ(|ξ|)t,whereξ∈R2is the horizontal spatial frequency andλ(|ξ|)＞0.This reduces the equations to a system of ordinary differential equations withλ(|ξ|)＞0 for eachξ.Then,solving the ODE system by the modified variational method,we show thatλ(|ξ|)＞0 is a continuous function on(0,|ξ|c),and the normal modes with spatial frequency grow in time,providing a mechanism for the Rayleigh-Taylor global instability,whereifκ＞0,otherwise|ξ|c=∞.Indeed,we can restrictξin some annulus domain,such thatλ(|ξ|)has a uniformly lower bound,and then we form a Fourier synthesis of the normal mode solutions constructed for each spatial frequencyξto give solutions to the linearized incompressible equations that grow in time,when measured inHk(Ω)for anyk≥0.Finally,we exploit the property of the boundary trace theorem to show a uniqueness result of the linearized problem(i.e.,Theorem 4.1),with the help of which we obtain the global instability of the corresponding nonlinear problem(i.e.,Theorem 2.2).In spite of the uniqueness,the linearized problem is globally unstable inHk(Ω)for anykin the sense of Hadamard.

With the linear global instability established,we can show the global instability of the corresponding nonlinear problem in some sense.Recalling that the steady state solution to(1.4)is given byη=0,u=0,p=constant,we now rewrite the nonlinear equations(1.4)in the form of perturbation around the steady state.Let

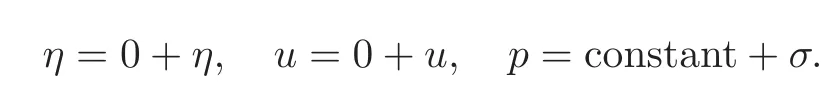
Then,the system(1.4)can be rewritten for(η,u,σ)as

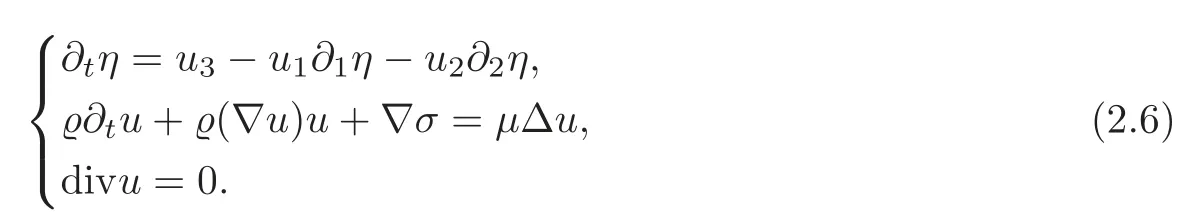
The jump conditions across the interface are

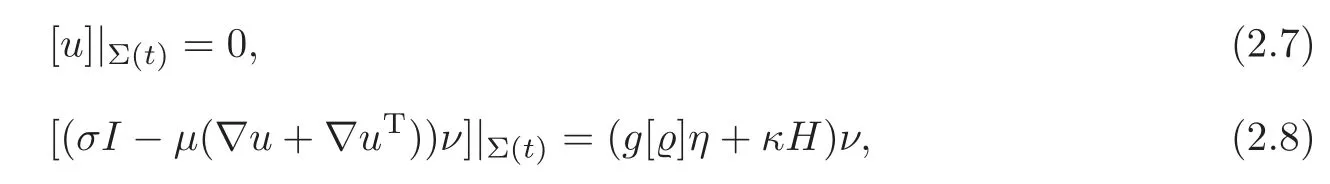
where

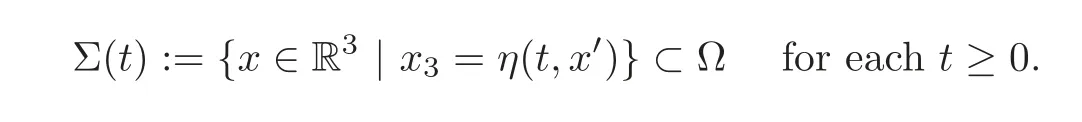
Finally,we require the boundary condition

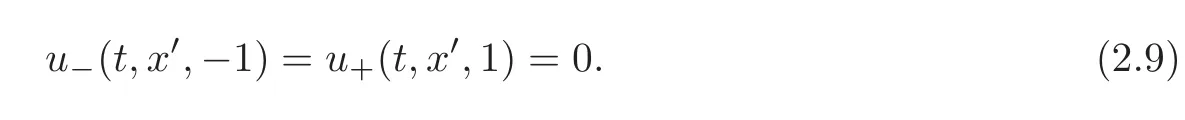
We collectively refer to the evolution,jump,and boundary equations(2.6)–(2.9)as “the perturbed problem”.

Definition 2.1We say that the perturbed problem has global stability of order k for some k≥3if there exist δ,C2＞0and a function F:[0,δ)→R+satisfying F(z)≤C2z for z∈[0,δ),so that the following holds:For any T＞0,η0,u0satisfying

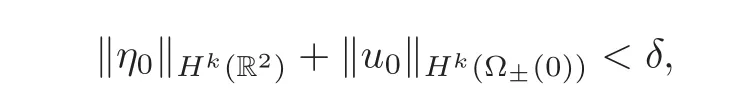
there exist η(t)and σ∈H1(Ω±(t))for any t∈[0,T],so that

(1)(η,u)(0)=(η0,u0),

(2)η,u,σ solve the perturbed problem(2.6)–(2.9),

(3)

(4)it holds that

The condition for global stability of orderkis quite general and is a reasonable choice for any global stability theory.The important feature of global stability of orderkis thatk≥3 is arbitrary.If the initial data are extremely smooth(kvery large),the failure of propertyEE(k)means that it is impossible to control even the norm offor allT＞0.Theorem 2.1 shows that the velocityuresults in the linear instability.However,it is still an open problem to show the nonlinear instability ofudue to technical diffculties.In this paper,we can show that the property of global stability of orderkcan not hold for anyk≥3,i.e.,the following Theorem 2.2,which will be proved in Section 5.

Theorem 2.2The perturbed problem does not have the property of global stability of order k for any k≥3.

The basic idea in the proof of Theorem 2.2 is to show,by utilizing the Lipschitz structure ofF,that the global stability of orderkwould give rise to certain estimates of solutions to the linearized equations(1.5)that can not hold in general because of Theorem 2.1.We will adapt and modify the arguments in[6]to prove Theorem 2.2.Compared with the perturbed problem in[6,Theorem 5.2]where the Lagrangian coordinates were used,our problem here is coupled to a free interface,rather than the fixed interface{x3=0}.As is well-known,the motion of the free surface Σ(t)and the domains Ω±(t)present several mathematical diffculties,so the authors[6]switched the perturbed problem in Eulerian coordinates to a perturbed problem in Lagrangian coordinates,in which the free interface is switched to the fixed interface{x3=0},while the domains of the upper and lower fluids stay fixed in time as Ω+=R2×(0,1)and Ω?=R2×(?1,0),respectively.Thus,the convergence for the jump conditions of the rescaled functions can be easily dealt with at the fixed interface in the proof of[6,Theorem 5.2].To circumvent such diffculties without the aid of the transform of Lagrangian coordinates,in a way similar to[15],we transform the perturbed equation in the second line of(2.6)to the integral form.Indeed,multiplying the second equation of(2.6)byφ,integrating by parts over(0,t0)×Ω,and using(2.7)–(2.9)together with the formula of surface integral,we obtain

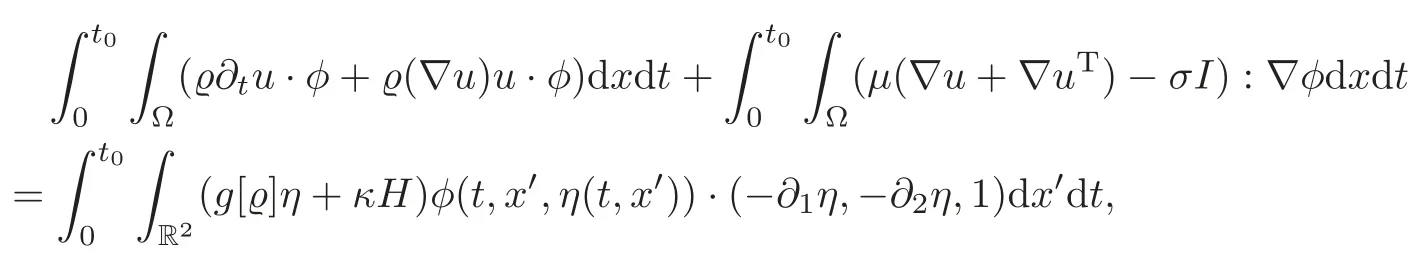
whereφ:=(φ1,φ2,φ3)∈(D′((0,T)×Ω))3,and

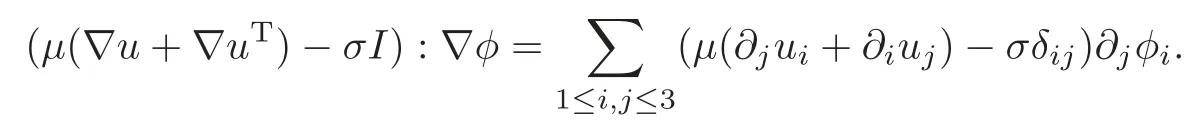
In this manner,we have transformed the two-fluid flow into a single-fluid flow in a fixed domain,which offers an alternative approach to deal with the jump condition(2.8)at the free interface Σ(t),instead of using the method of Lagrangian coordinates in[6,8].Consequently,we can avoid the proof of convergence for the jump conditions of the rescaled viscous stress-tensor at the free boundary.This transform will play an important role in the proof of Theorem 2.2 in Section 5.Moreover,this idea is also applied to the proof of the uniqueness of solutions to the linearized equations(1.5)in Section 4.

We mention that Guo and Tice[8]recently proved the linear global instability for compressible viscous fluids in Lagrangian coordinates,while in the current paper the nonlinear global instability for incompressible viscous fluids in the sense of Definition 2.1 is established in Eulerian coodinates.Prüess and Simonett[17]developed another coordinate transformation to transform the free boundary problem(1.1)in Ω=R3to a fixed boundary problem(1.1),and then proved the nonlinear instability in the abstract Sobolev-Slobodeckii spaces for the transformed problem.Later,Tice and Wang[21]provided an alternative proof to show the nonlinear instability in the natural energy space for the horizontally periodic setting.It should be noted that we does not use any coordinate transformation in this paper.Finally,we point out that Hwang and Guo[9]constructed an unstable solution to show mathematically the Rayleigh-Taylor instability for two-dimensional incompressible inviscid flows when the density is continuous.It still needs further study whether we can construct a concrete solution to(2.6)–(2.9)which does not have global stability of orderk.

3 Construction of a Growing Solution to the Linearized Equations

3.1 Growing mode ansatz

We wish to construct a solution to the linearized equations(1.5)that has a growingHknorm for anyk.We will construct such solutions via Fourier synthesis by first constructing a growing mode for the fixed spatial frequency.

To begin with,we make a growing mode ansatz,i.e.,let us assume that

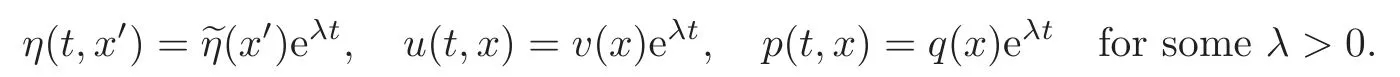
Substituting this ansatz into(1.5),and eliminatingby using the first equation,we arrive at the time-invariant system forv=(v1,v2,v3)andq:

with the corresponding jump conditions

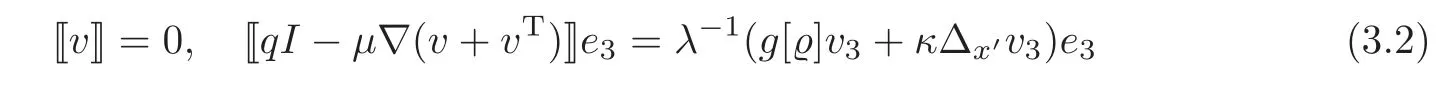
and boundary conditions

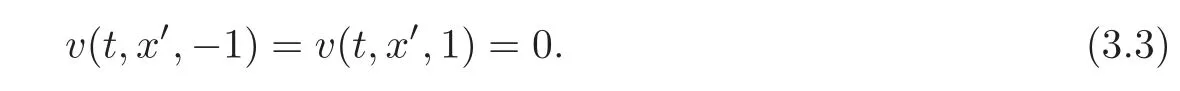
3.2 Horizontal Fourier transform

We take the horizontal Fourier transform of(v1,v2,v3)in(3.1),which we denote with eitherorF,and fix a spatial frequencyξ=(ξ1,ξ2)∈R2.Define the new unknowns

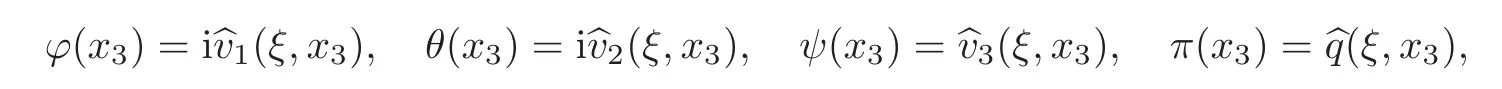
so that

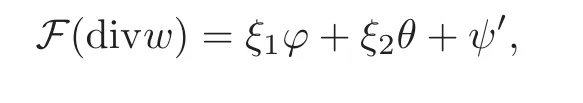
whereThen,for?,θ,ψandλ=λ(ξ),we can deduce from(3.1)–(3.3)that

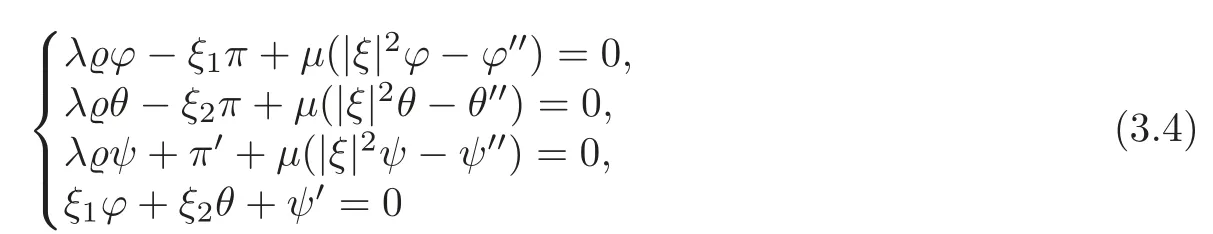
along with the jump conditions

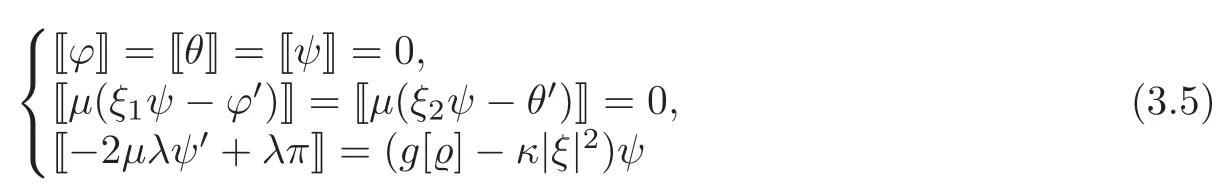
and the boundary conditions

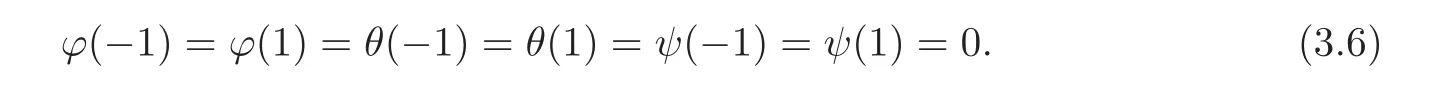
Eliminatingπfrom the third equation in(3.4),we obtain the following ODE forψ:

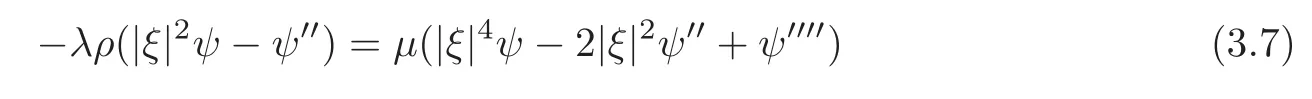
along with the jump conditions

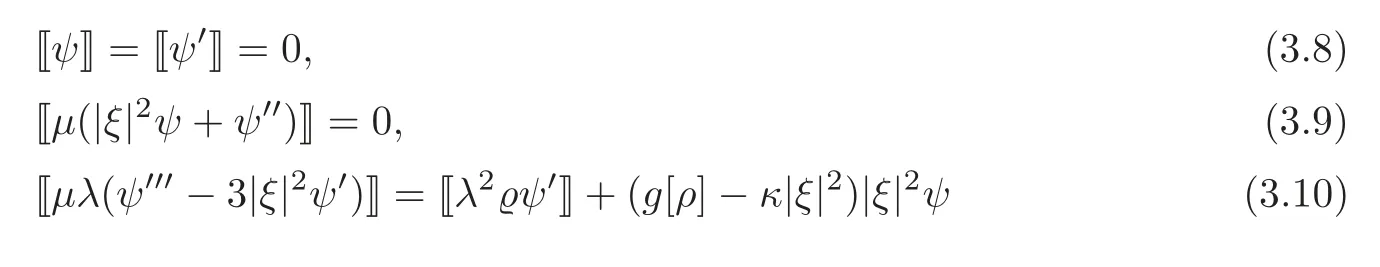
and the boundary conditions

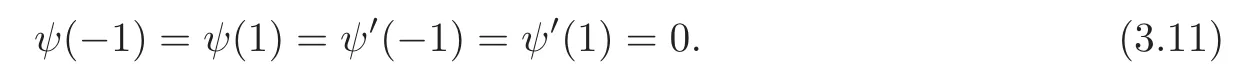
3.3 Construction of a solution to the fourth order ODE

In a way similar to[8,23],we can apply the variational methods to construct solutions to(3.7)–(3.11).The idea of the proof can be found in the pioneering paper due to Guo and Tice[8],which was later adapted by Wang[23].For the reader’s convenience,we sketch the outline of the construction.

First,fix a non-zero vectorξ∈R2ands＞0.From(3.7)–(3.11),we get a family of the modified problems

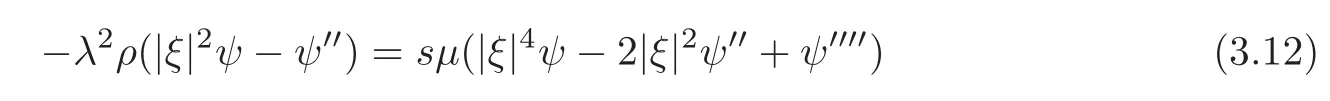
along with the jump conditions

and the boundary conditions

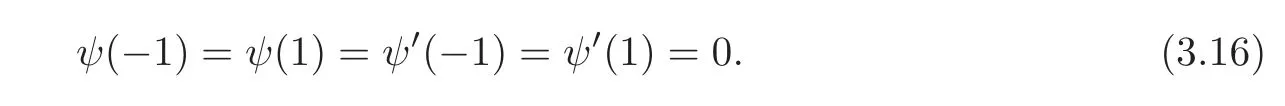
We define the energy functional of(3.12)by

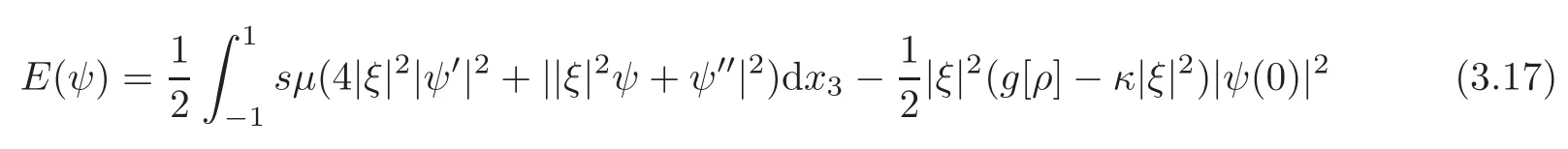
with the associated admissible set

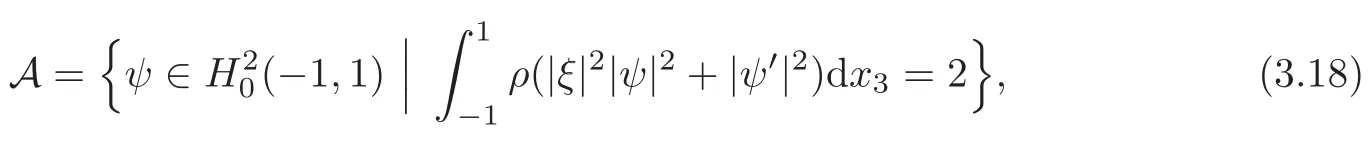
whereis the subset ofH2(?1,1)satisfying(3.16).Thus we can find a?λ2by minimizing

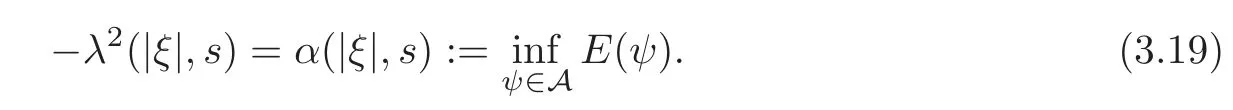
In fact,we can show that a minimizer of(3.19)exists,and that the minimizer satisfies Euler-Lagrange equations equivalent to(3.12)–(3.16).

Proposition 3.1For any fixed ξ/=0and s＞0,E achieves its inf i nimum on A.In addition,let ψ be a minimizer and?λ2:=E(ψ),and then the pair(ψ,λ2)satisfies(3.12)along with the jump and boundary conditions(3.13)–(3.16).Moreover,ψis smooth when restricted to(?1,0)or(0,1).

ProofWe can follow the same proof procedure as in[8,Propostition 3.2](or[23,Proposition 3.1])to show Proposition 3.1.Hence,we omit the details of the proof here.

Next,we want to prove that there is a fixed point,such thatλ=s.To this end,we shall give some properties ofα(s)as a function ofs＞0.

Proposition 3.2is strictly increasing.Moreover,

(1)for any a,b∈(0,|ξ|c)with a＜b,there exist constants c1,c2＞0depending on ?±,μ±,g,a and b,such that

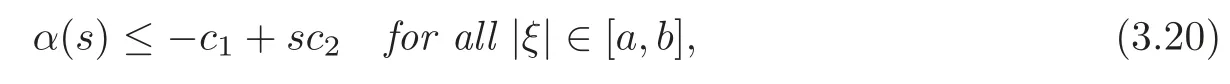
where

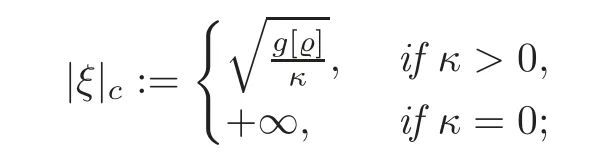
(2)there exist constants c3＞0depending on ?±and g,c4＞0depending additionally on μ±and|ξ|,such that

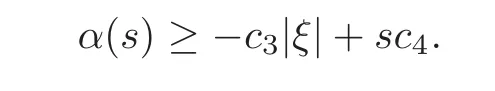
ProofWe refer to[8,Propostition 3.6](or[23,Lemma 3.5])for the proof.

Givenξ∈R2with|ξ|∈(0,|ξ|c),by virtue of(3.20),there exists ans0＞0 depending on the quantities?±,μ±,g,|ξ|,so that fors≤s0,it holds thatα(s)＜0.Hence,we can define the open set

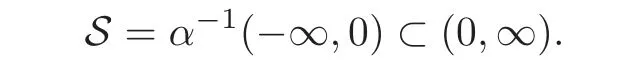
Note thatSis non-empty and this allows us to definefors∈S.Therefore,as a result of Proposition 3.1,we have the following existence result for the modified problem(3.12)–(3.16).

Proposition 3.3For each ξ∈R2with|ξ|∈(0,|ξ|c)and each s∈S,there exists a solution ψ=ψ(|ξ|,x3)with λ=λ(|ξ|,s)＞0to the problem(3.12)with the jump and boundary conditions(3.13)–(3.16).Moreover,ψ is smooth when restricted to(?1,0)or(0,1)with ψ(|ξ|,0)/=0.

Finally,we can use Proposition 3.2 to make a fixed-point argument to finds∈Ssuch thats=λ(|ξ|,s)to construct solutions to the original problem(3.7)–(3.11).

Proposition 3.4Let ξ∈R2with|ξ|∈(0,|ξ|c),and then there exists a unique s∈S sothatand s=λ(|ξ|,s).

ProofWe refer to[8,Theorem 3.8](or[23,Lemma 3.7])for a proof.

Consequently,in view of Propositions 3.3–3.4,we conclude the following existence result concerning the problem of(3.7)–(3.11).

Theorem 3.1For each ξ∈R2with|ξ|∈(0,|ξ|c),there exist ψ=ψ(|ξ|,x3)and λ(|ξ|)＞0satisfying(3.7)–(3.11).Moreover,ψis smooth when restricted to(?1,0)or(0,1)with ψ(|ξ|,0)/=0.

Next,we show some properties of the solutions established in Theorem 3.1 in terms ofλ(|ξ|).The first property is given in the following proposition which shows thatλis a bounded continuous function of|ξ|.

Proposition 3.5The function λ:(0,|ξ|c)→(0,∞)is continuous and satisfies

Moreover,

and if κ＞0,then also

ProofThe continuity and the limits(3.22)–(3.23)follow from the same arguments as in[8,Proposition 3.9]with the help of(3.7)–(3.21)and Ehrling-Nirenberg-Gagliardo interpolation inequality.To complete the proof,it suffces to show(3.21).For each|ξ|∈(0,|ξ|c),there exists a functionψ|ξ|∈Asatisfying(3.7)–(3.11),so that?λ2(|ξ|)=E(ψ|ξ|).By(3.17),we find that

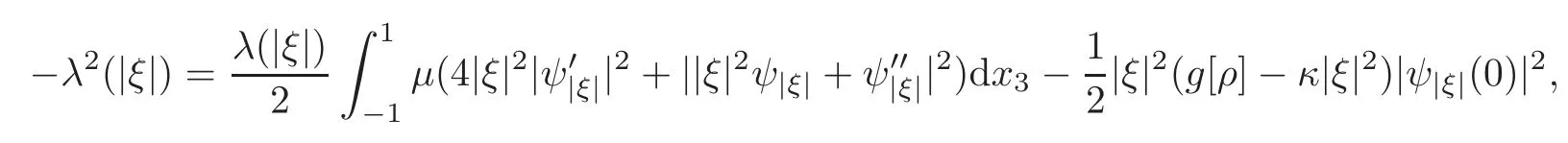
which yields

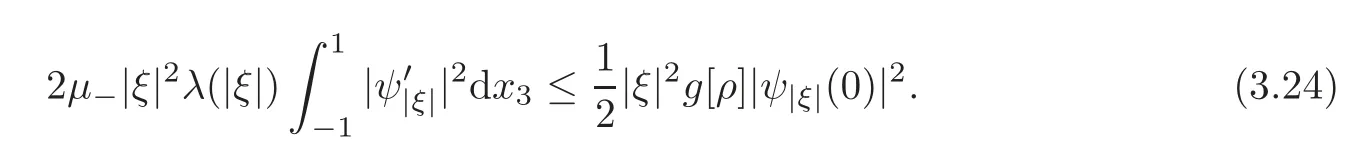
Using the H?lder inequality,we can bound

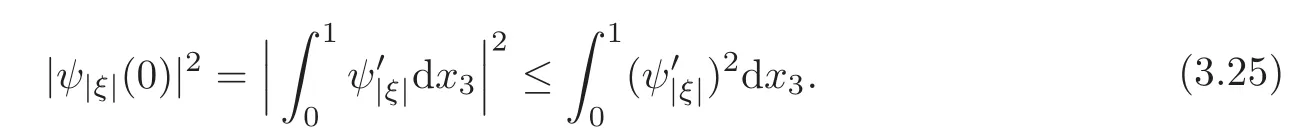
Substituting(3.25)into(3.24)gives then

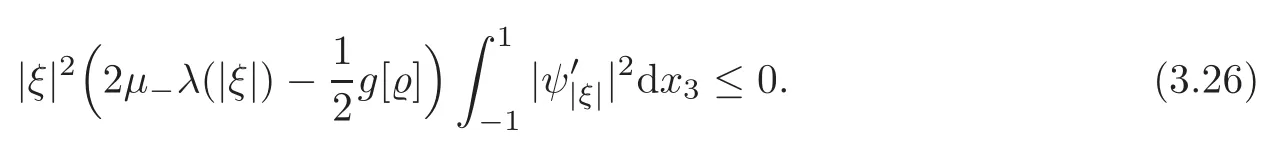
Consequently,(3.26)implies(3.21),since‖ψ′|ξ|‖L2(?1,1)＞0.

3.4 Construction of a solution to the system(3.4)–(3.6)

A solution to(3.7)–(3.11)gives rise to a solution to the system(3.4)–(3.6)for the growing mode velocityv,as well.

Theorem 3.2For each ξ∈R2with|ξ|∈(0,|ξ|c),there exists a solutionwith λ=λ(|ξ|)＞0to(3.4)–(3.6),and the solution issmooth when restricted to(?1,0)or(0,1).Moreover,

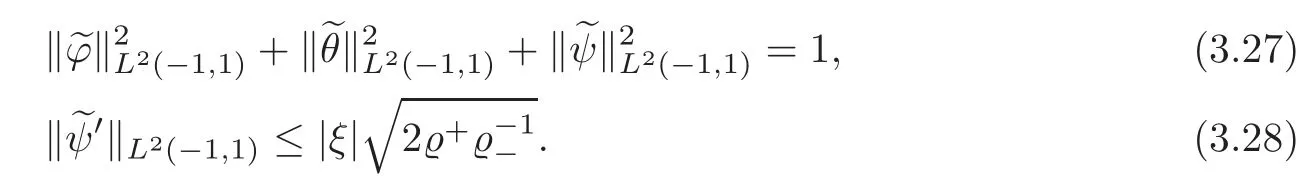
ProofBy Theorem 3.1,we first construct a solution(ψ,λ)=(ψ(|ξ|,x3),λ(|ξ|))satisfying(3.7)–(3.11).Moreover,λ＞0 andψ∈Ais smooth when restricted to(?1,0)or(0,1).Then,multiplying the first and second equations in(3.4)byξ1andξ2respectively,adding the resulting equations,and utilizing the fourth equation in(3.4),we find thatπcan be expressed byψ,i.e.,

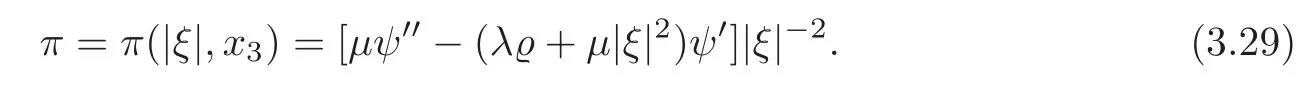
Notice that the first equation in(3.4)can be rewritten as

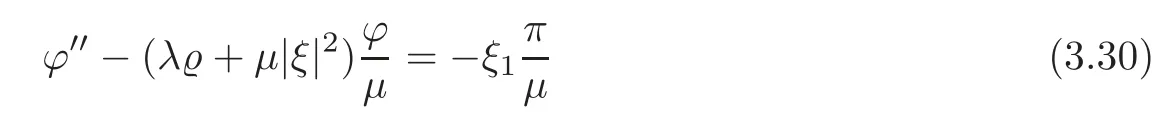
with jump and boundary conditions

Hence,we can easily construct a unique solution

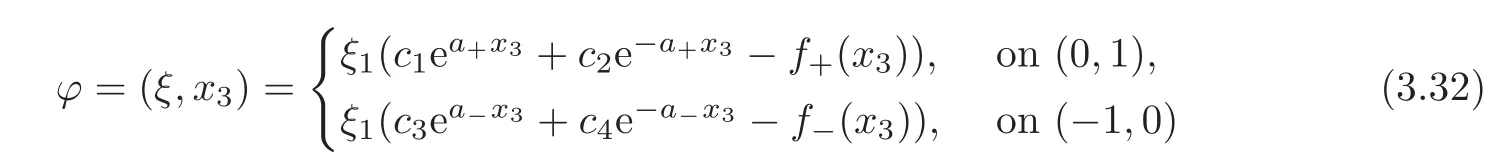
to the equation(3.30)with jump and boundary conditions(3.31),where

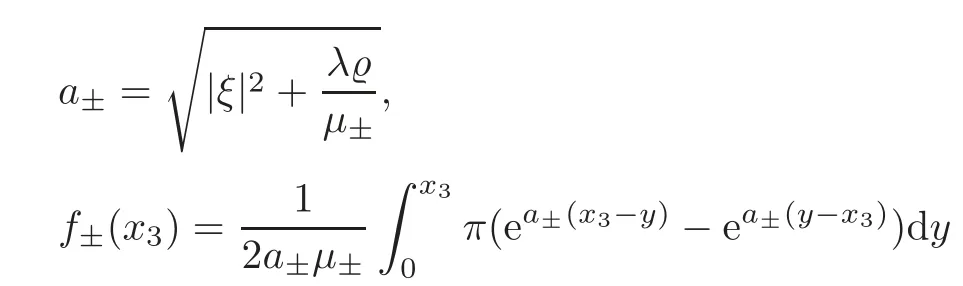
and

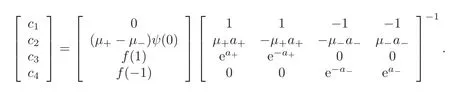
In the way similar to(3.32),

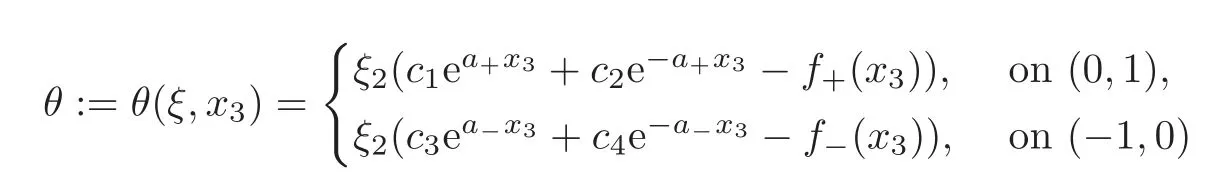
is a unique solution to the second equation in(3.4)with jump and boundary conditions:

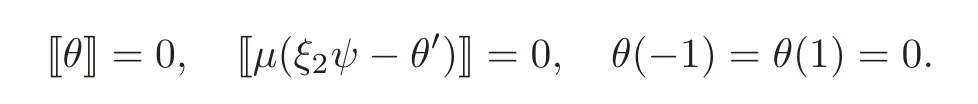
Consequently,(?,θ,ψ,π)is a solution to the system(3.4)–(3.6).Now,we define

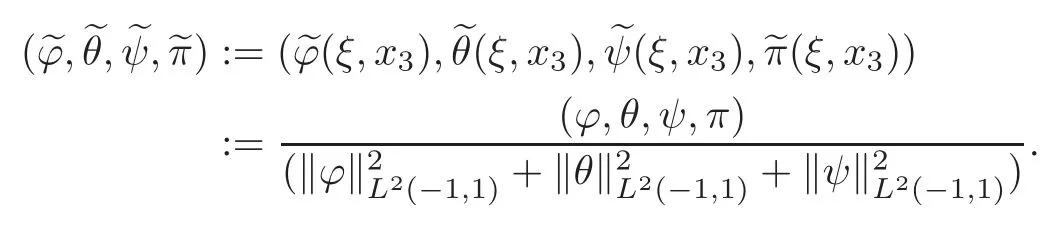
Thus,is still a solution to the system(3.4)–(3.6),and moreover,satisfies(3.27).

Finally,making use of the fourth equation in(3.4)and(3.18),we conclude that

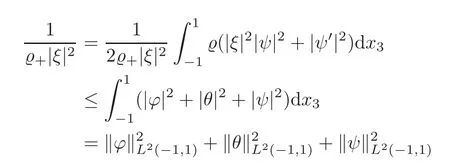
and

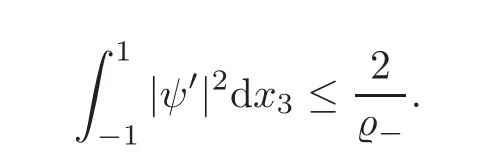
The above two inequalities imply(3.28)immediately.

Remark 3.1For eachx3,it is easy to see that the solutionλ(|ξ|))constructed in Theorem 3.2 has the following properties:

(1)andare even onξ1orξ2,when the other variable is fixed;

(2)is odd onξ1,but even onξ2,when the other variable is fixed;

(3is even onξ1,but odd onξ2,when the other variable is fixed.

To directly estimate theHknorm of the solutionψfrom(3.7),without use of(3.17)and the continuity ofλ,we shall apply the following Ehrling-Nirenberg-Gagliardo interpolation inequality,the proof of which can be found in[1,Chapter 5].

Lemma 3.1LetΩbe a domain inRnsatisfying the cone condition.For each ε0＞0,there exists a constant K depending on n,m,p and ε0,such that if0＜ε ≤ε0,0≤j≤m and u∈Wm,p(Ω),then

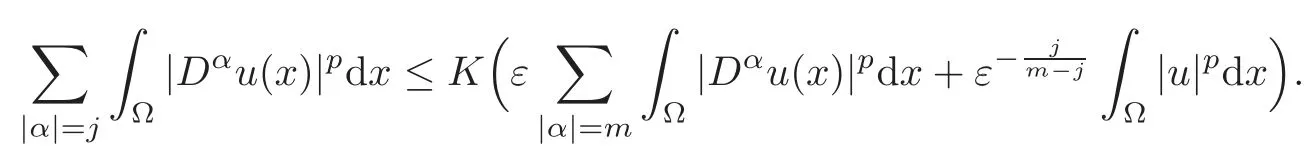
The next lemma provides an estimate for theHknorm of the solutionwithξvarying,which will be useful in the next section when such a solution is integrated in a Fourier synthesis.To emphasize the dependence onξ,we write these solutions as

Lemma 3.2Let ξ∈R2with0＜R1＜|ξ|＜|ξ|c,?(ξ):=and λ(|ξ|)be constructed as in Theorem3.2,and then for any k≥0,there existpositive constants ak,bkand ckdepending on R1,?±,μ±and g,so that

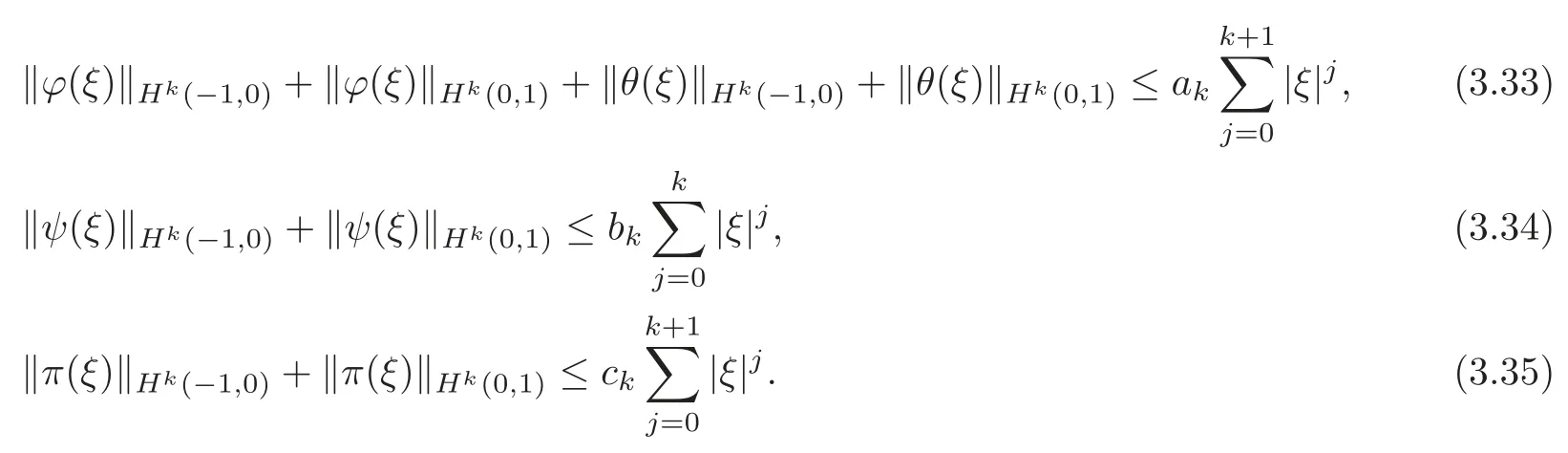
Moreover,

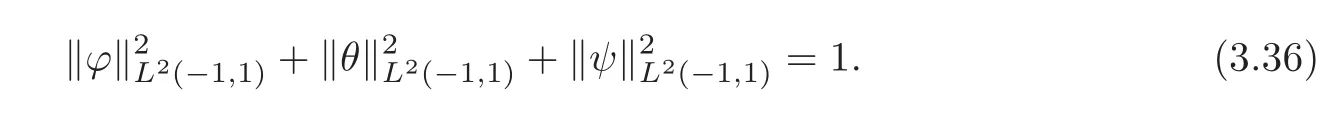
ProofThroughout this proof,we denote bygeneric positive constants which may depend onR1,?±,μ±andg,but not on|ξ|.

(i)First,(3.36)follows from(3.27)immediately.We now write(3.7)as

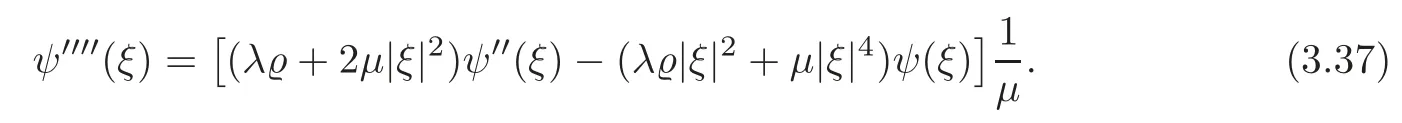
If we make use of(3.21),|ξ|＞R1and Lemma 3.1,then we see that there exists a couplesuch that

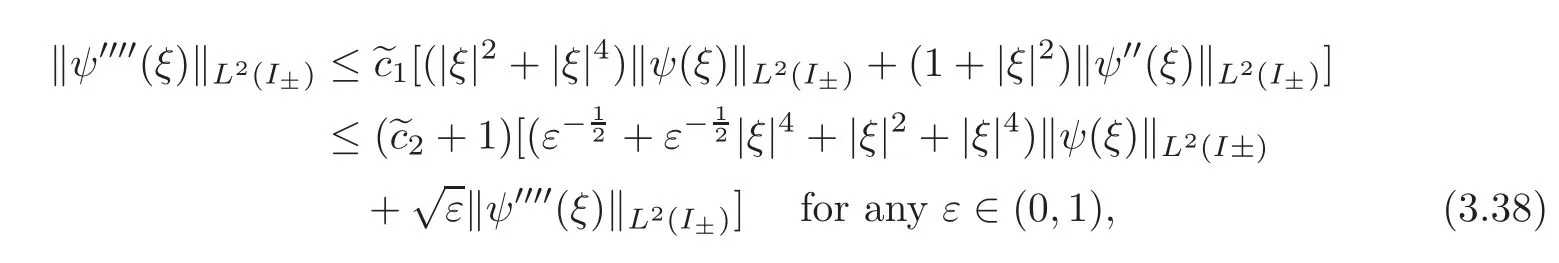
respectively,whereI+=(0,1)andI?=(?1,0).Choosingin(3.38)and using(3.36),we arrive at

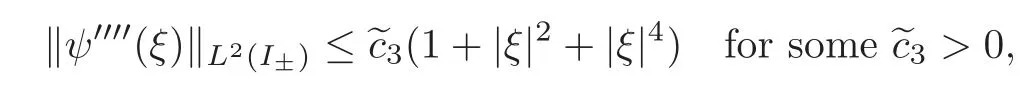
whence,

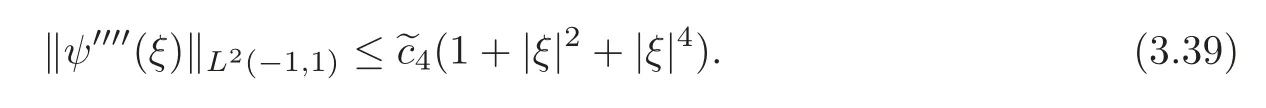
Writing(3.37)as

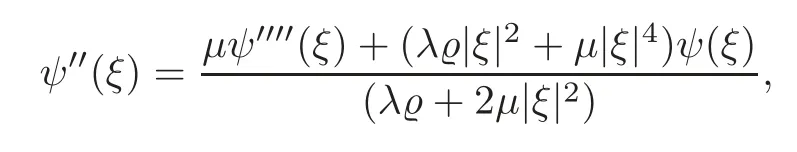
we utilize(3.39)and(3.36)to get

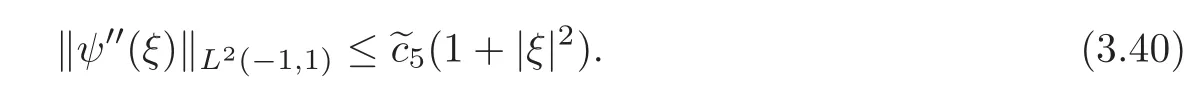
Differentiating(3.37)with respect tox3,we see that

In a way similar to(3.39)–(3.40),we obtain,by Lemma 3.1,(3.21),(3.28)and(3.36),that

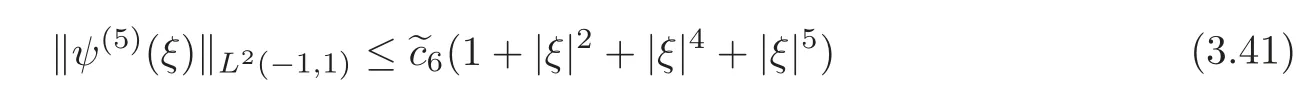
and

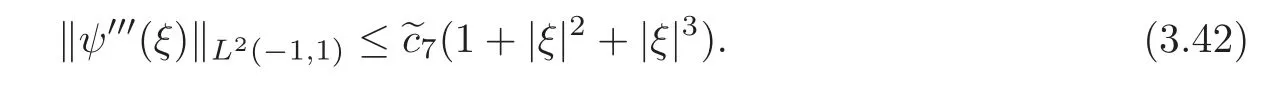
Summarizing the estimates(3.28),(3.36)and(3.39)–(3.42),we conclude that,for each nonnegative integerk∈[0,5],there exists a constant＞0 depending onR1,?±,μ±andg,such that

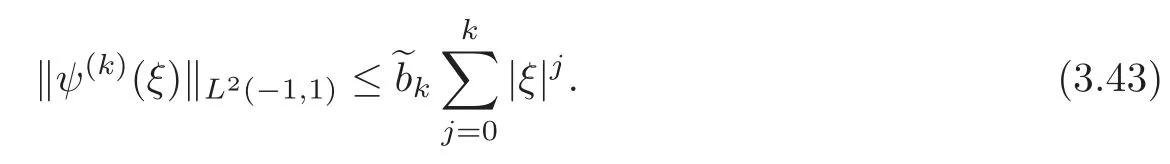
Differentiating(3.37)with respect tox3and using(3.43),we find,by induction onk,that(3.43)holds for anyk≥0.This gives(3.34).

(ii)Recalling the expression(3.29)ofπand the fact that|ξ|＞R1,we employ(3.34)to deduce that for anyk≥0,

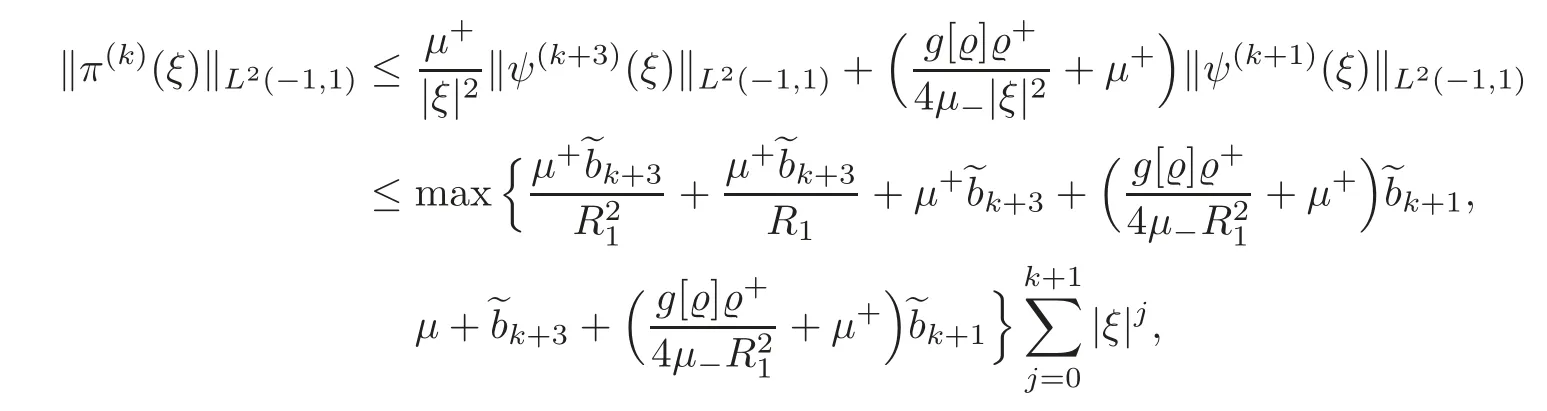
which implies(3.35).

(iii)From(3.21),(3.30),(3.35)–(3.36),we get

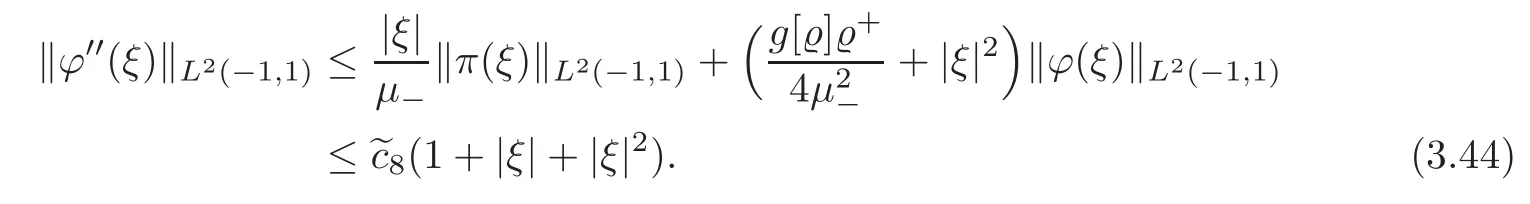
Applying(3.44),(3.36)and Lemma 3.1,we obtain

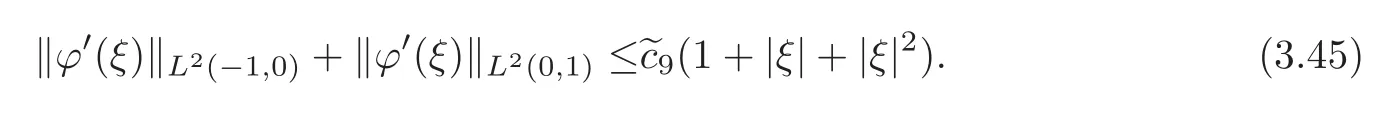
Combining(3.36)with(3.44)–(3.45),we conclude that,for each nonnegative integerk∈[0,2],there exists a constant＞0 depending onR1,?±,μ±andg,so that

Thus,by virtue of(3.30),(3.46)and induction onk,(3.46)holds for anyk≥0.Following the same procedure as used in estimating?,we infer that for eachk≥0,

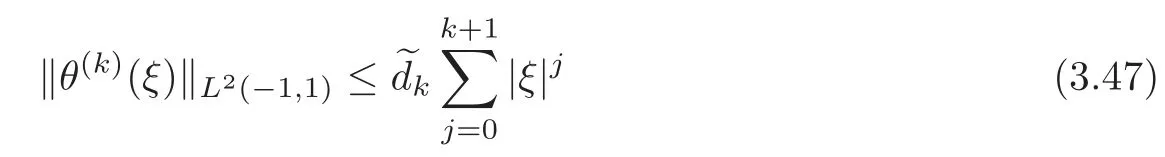
for some constantdepending onR1,?±,μ±andg.Adding(3.47)to(3.46),we arrive at

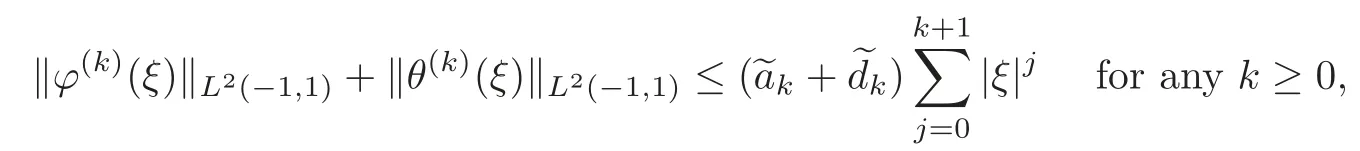
which yields(3.33).This completes the proof.

3.5 Fourier synthesis

In this section,we will use the Fourier synthesis to build growing solutions to(1.5)out of the solutions constructed in the previous section(Theorem 3.2)for the fixed spatial frequencyξ∈R2with|ξ|∈(0,|ξ|c).The constructed solutions will grow in time in the piecewise Sobolev space of orderk,Hk(Ω±),defined by(2.1).

Theorem 3.3Let0＜R1＜R2＜|ξ|candbe a real-valued function.Forξ∈R2with|ξ|∈(0,|ξ|c),define

where(?,θ,ψ,π)(ξ,x3):=is the solution given by Theorem3.2.Denote

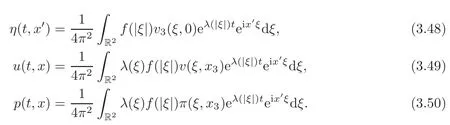
Then,(η,u,p)is a real-valued solution to the linearized problem(1.5)along with the corresponding jump and boundary conditions.For every k∈N,we have the estimate

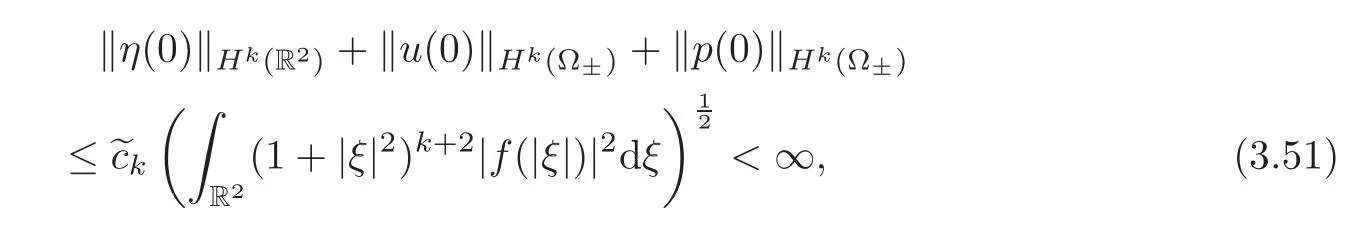
where＞0is a constant depending on the parameters ?±,R1and g.Moreover,for every t＞0,we have η(t)∈Hk(R2),u(t),p(t)∈Hk(Ω±),and

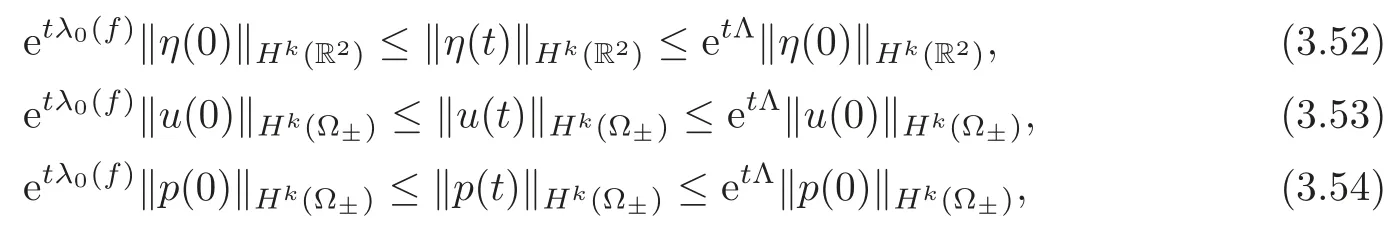
where

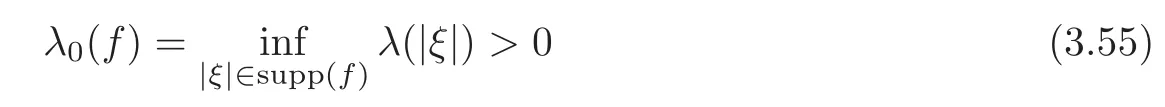
and

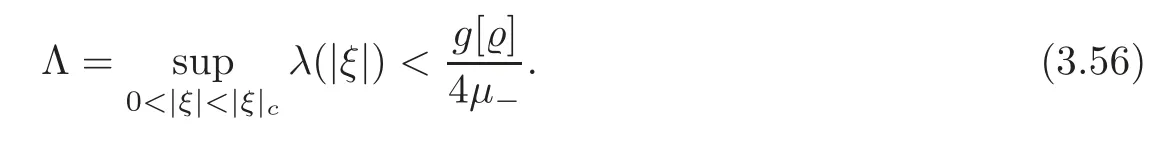
ProofBy virtue of Proposition 3.5,(3.55)–(3.56)hold.For each fixedξ∈R2,

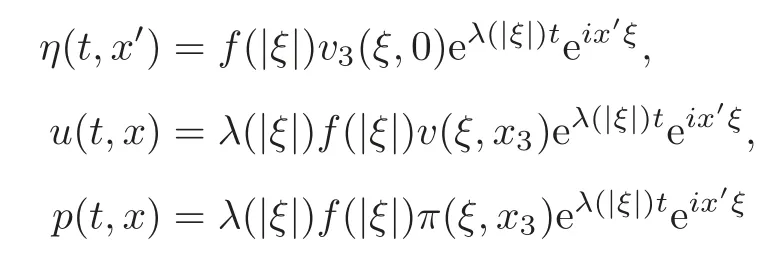
give a solution to(1.5).SinceLemma 3.2 implies that

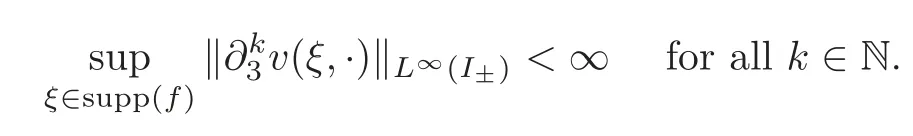
Also,λ(ξ)≤Λ.These bounds show that the Fourier synthesis of the solution given by(3.48)–(3.50)is also a solution to(1.5).Becausefis real-valued and radial,combined with Remark 3.1,we can easily verify that the Fourier synthesis is real-valued.

The estimate(3.51)follows from Lemma 3.2 with an arbitraryk≥0 and the fact thatfis compactly supported.Finally,we can use(3.55)–(3.56)and(3.48)–(3.50)to obtain the estimates(3.52)–(3.54).

4 Global Instability for the Linearized Problem

4.1 Uniqueness of linearized equations

In this subsection,we will show the uniqueness of solutions to the linearized problem,which will be applied to prove Theorem 2.2 in Section 5.For this purpose,we need a generalized formula of integrating by parts(or Gauss-Green formula).Let us first recall the boundary trace theorem(see Theorem 5.36 in[1,Chapter 5]).

Lemma 4.1Let U be a domain inRnsatisfying the uniform Cm-regularity condition,and assume that there exists a simple(m,p)-extension operator E for U.Also assume that mp＜nandThen,there exists a bounded linear operator

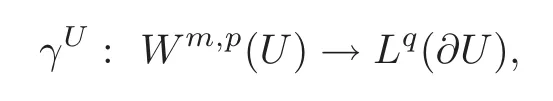
such that

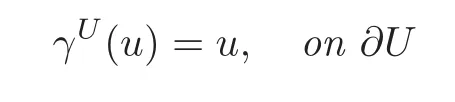
for all u∈Wm,p(U)∩C

The functionγU(u)∈Lq(?U)is called the trace of the function ofu∈W1,p(U)on the boundary?U.By the Stein extension theorem(see Theorem 5.24 in[1,Chapter 5])and the definition of the uniformCm-regularity condition(see Definition 4.10 in[1,Chapter 5]),it is easy to verify that Ω, Ω+and Ω?have different simple(m,p)-extension operators.Keeping these facts in mind,we can start to show the following formula of integrating by parts.For convenience in the subsequent analysis,we will use the notationsγ+(f):=γΩ+(f+)andγ?(f):=γΩ+(f?).

Lemma 4.2For all u∈(Ω)and w∈H1(Ω±),we have

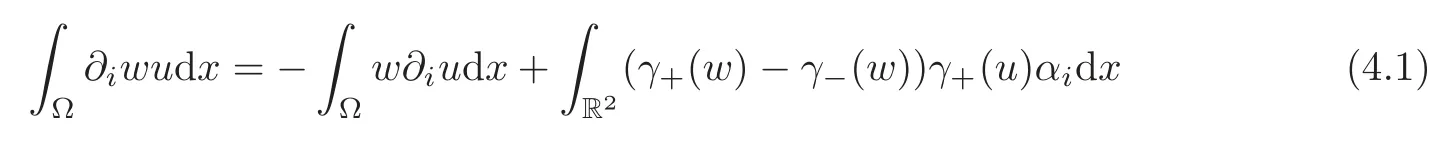
for i=1,2,3,where α1=α2=0and α3=?1.

ProofTemporarily supposeBy the Gauss-Green theorem,we have

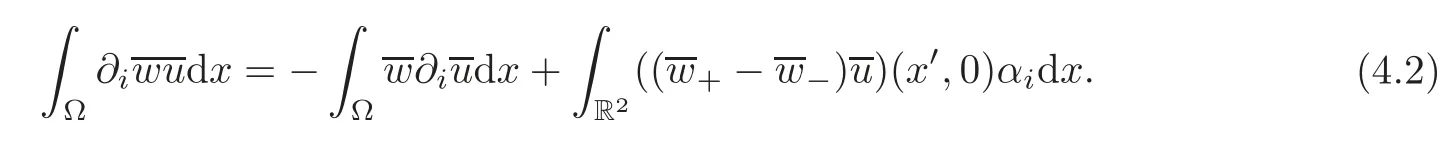
Using Lemma 4.1,one has

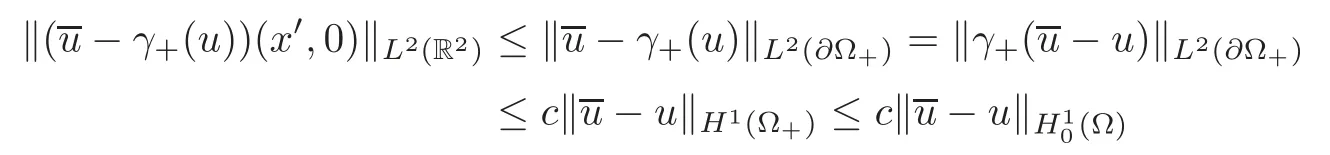
and

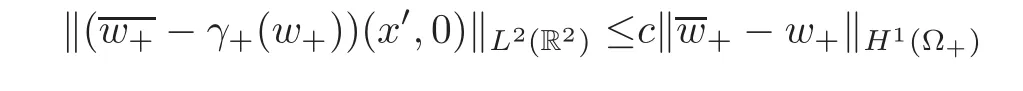
for some constantc＞0.By the H?lder inequality,the above two estimates imply that

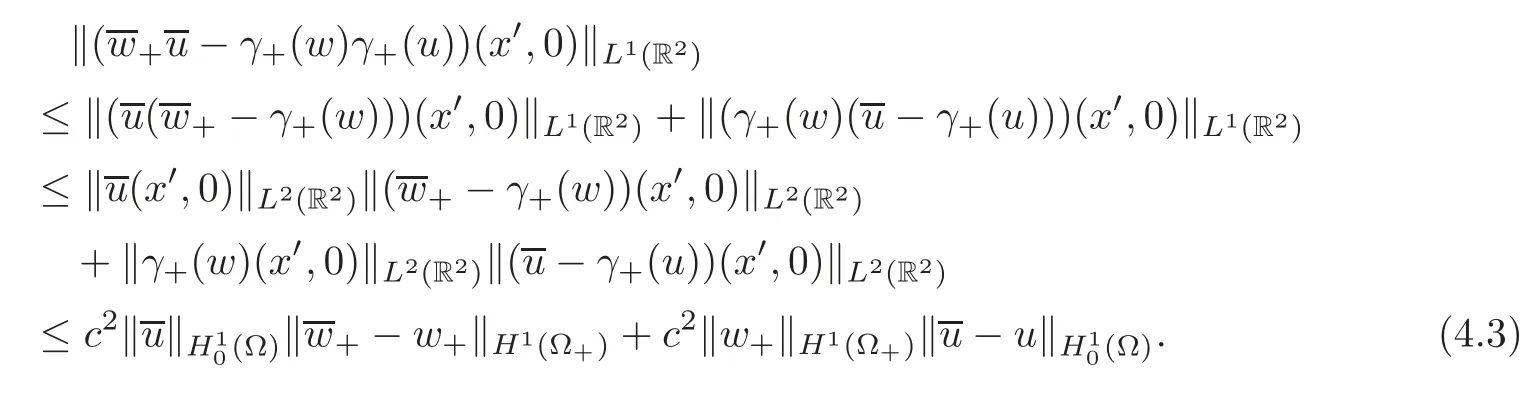
In a way similar to(4.3),one gets

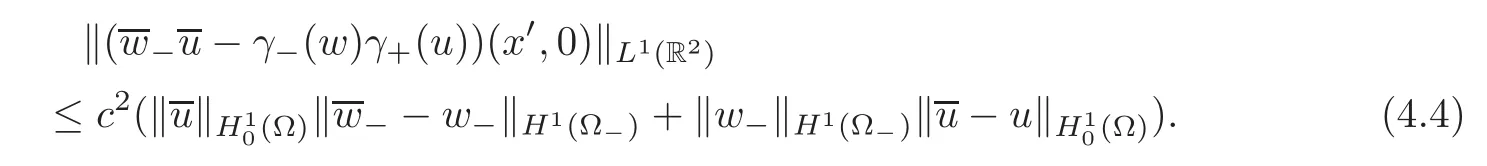
In addition,if→ustrongly inthen there exists anm0＞0,such that

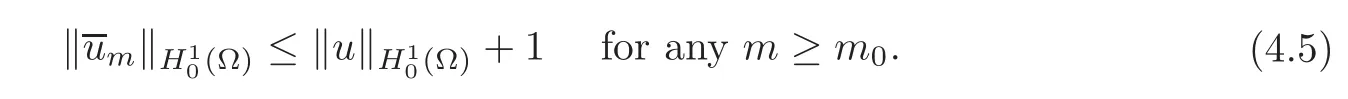
Note that sinceC0(Ω)is dense in(Ω)andis dense inH1(Ω+)orH1(Ω?),thus(4.1)follows from(4.2)–(4.5),using a standard density argument.

Definition 4.1Given t0＞0and the initial datum(η0,u0)to the linearized problem(1.5)–(1.7),a triple(η,u,p)is called a strong solution of(1.5)–(1.7),if

(1)η∈C0([0,t0],

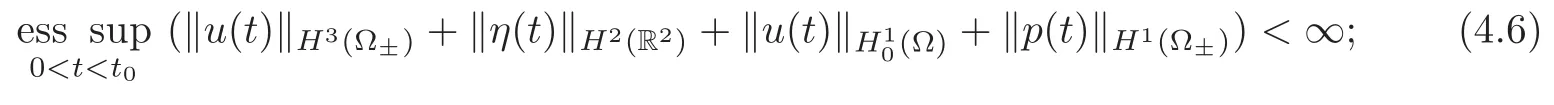
(2)the equations

hold a.e.in(0,t0)×(Ω{x3=0});

(3)for a.e.t∈(0,t0),

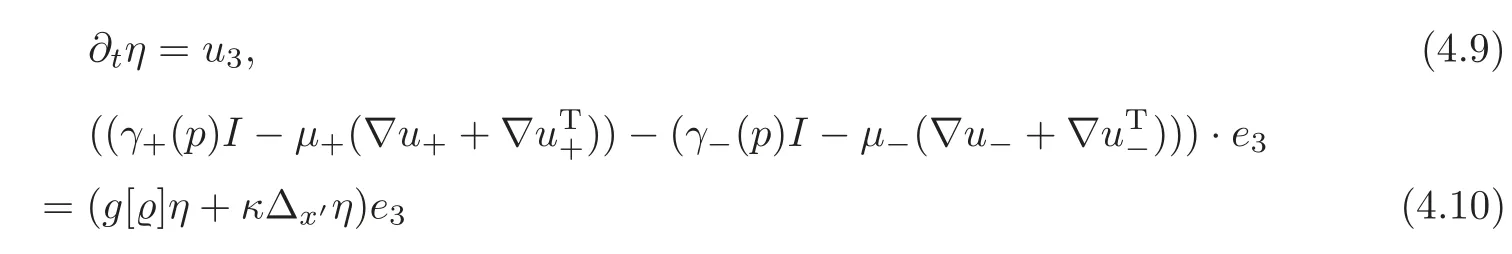
hold a.e.inR2×{x3=0},where u3is the third component of u.

Remark 4.1Sinceu(t)∈∩H3(Ω±)for eacht≥0,we can make use of the embedding theorem and(4.8)to obtain

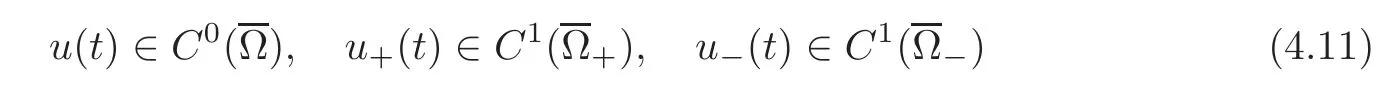
and

Thus,in view of(4.13),we define for the sake of simplicity that

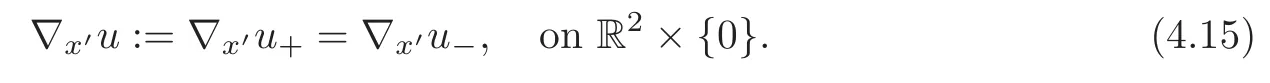
Moreover,by virtue of Lemma 4.1,there exists a constantcsuch that

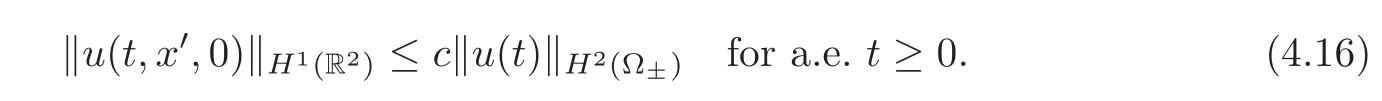
Remark 4.2It is easy to verify that any(η,u,p),which is a solution established in Theorem 3.3,is a strong solution to the linearized system(1.5)–(1.7).

Theorem 4.1Assume that(η1,v,p1)and(η2,w,p2)are two strong solutions to(1.5)–(1.7),with v(0)=w(0)=u0and η1(0)=η2(0)=η0.Then,(η1,v,p1)=(η2,w,p2+c)for some constant c.

ProofLet(η,u,p)=(η1?η2,v?w,p1?p2).Recalling Definition 4.1,(η,u,p)is still a strong solution to the linearized system(1.5)–(1.7)with zero initial data,i.e.,η(0)=0 andu(0)=0.

Multiplying(4.7)byu,integrating over(0,τ)×Ω for anyτ∈(0,t0)and using(4.14),we find that

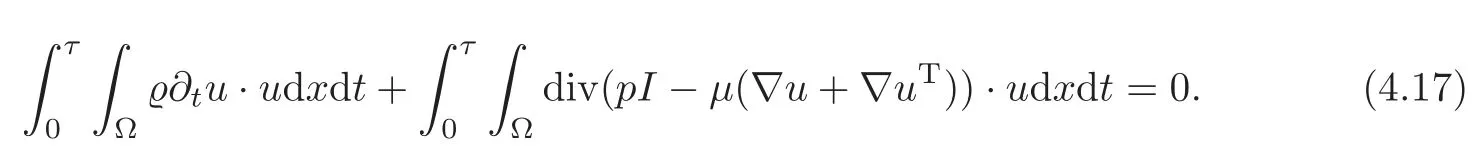
Thanks to Lemma 4.1,(4.11)–(4.14)and the regularity ofp,we obtain

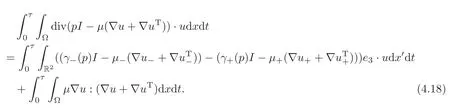
Notice that in view of(4.6),p(t)∈(H1(Ω±))3andu(t)∈(H2(Ω±))3for a.e.t＞0.Thus,(4.7)implies that

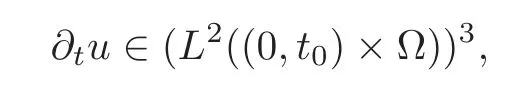
which,together withu∈L∞(0,t0;(H1(Ω))3)∩C0([0,t0],(L2(Ω))3),yields

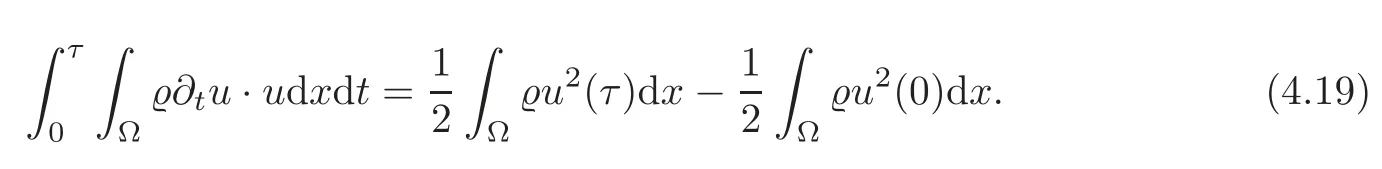
In view of(4.10),(4.17)–(4.19)andu(0)=0,we find that

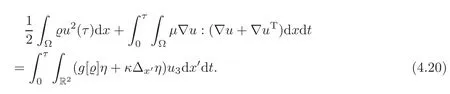
Sinceandη(0)=0,the equation(4.9)implies that

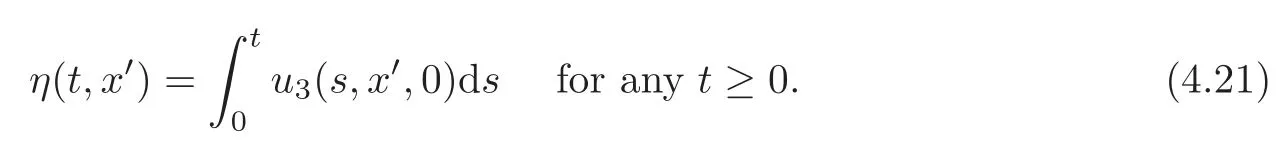
Using(4.15)–(4.16),(4.21)and the regularity ofη,we infer that

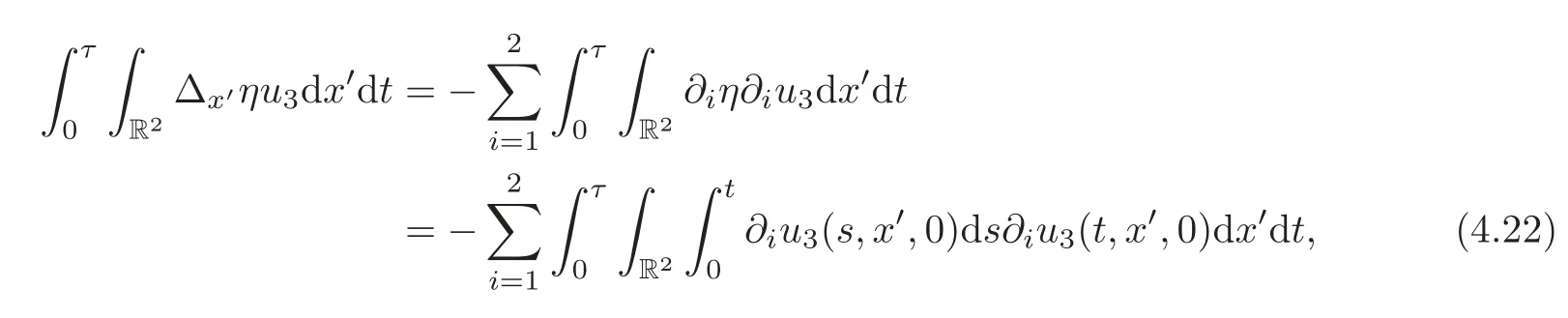
where the formula of integration by parts can be shown in the same manner as in Lemma 4.1.

Consequently,inserting(4.21)–(4.22)into(4.20),we arrive at

With the help of the regularity of?iu3,the property of absolutely continuous functions and the Fubini theorem,we conclude that

On the other hand,applying the Cauchy-Schwarz inequality,we get

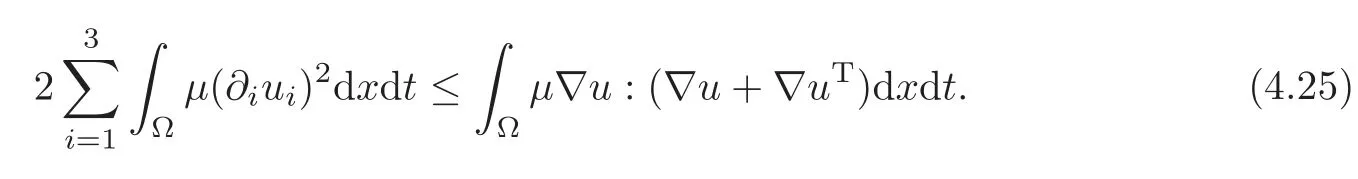
Hence,by(4.23)–(4.25),we have

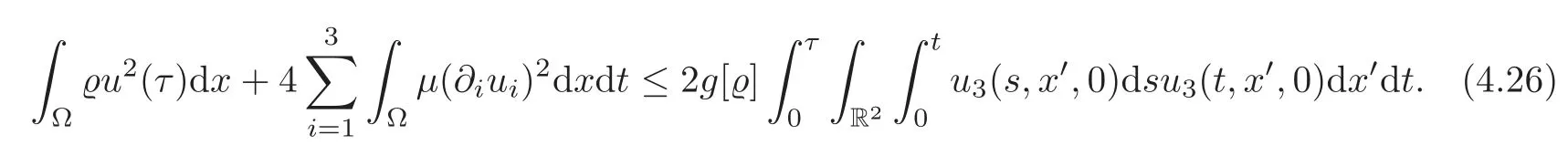
In a way similar to(4.24),the right-hand side of(4.26)can be bounded as follows:

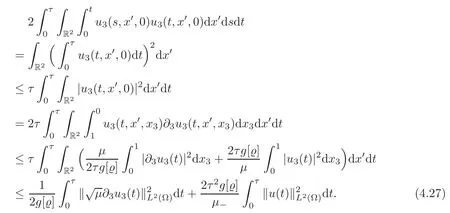
Substituting(4.27)into(4.26),we deduce

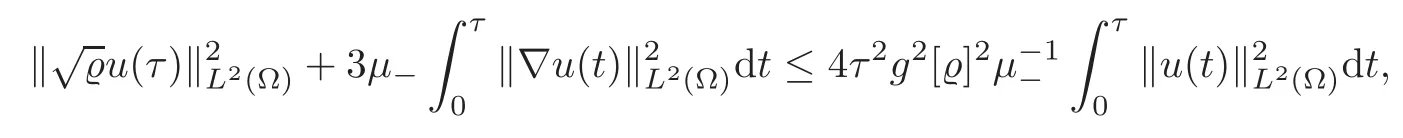
which results in

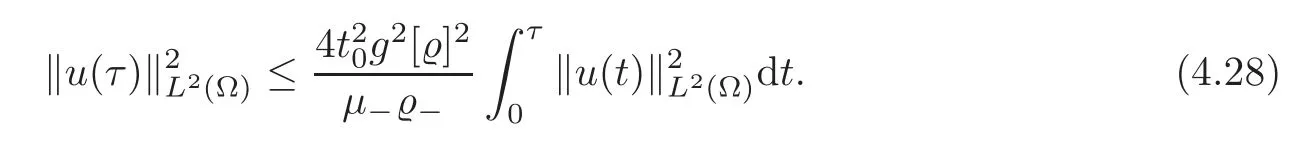
Moreover,if we apply the Gronwall inequality to(4.28),we obtain

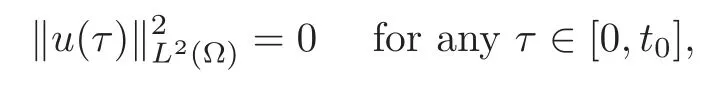
which impliesu=0,i.e.,v=w.This,combined with(4.7)and(4.9),proves Theorem 4.1.

Remark 4.3In addition,employing arguments similar to those used for(4.1),the regularity ofustated in Remark 4.1 and the fact that divu=0,we can show

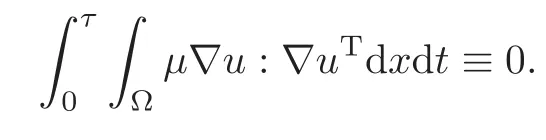
4.2 Proof of Theorem 2.1

We define

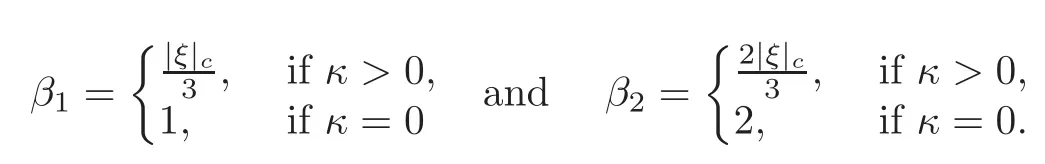
Fixj≥k≥0,α＞0 and letbe the constants from Theorem 3.3.For eachn∈N,lettnbe suffciently large,so that

i.e.,

where

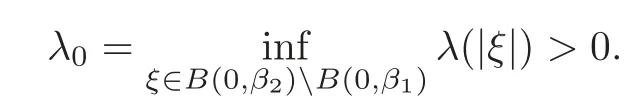
Choosesuch that supp(fn)?B(0,β2)B(0,β1),fnis real-valued and radial,and

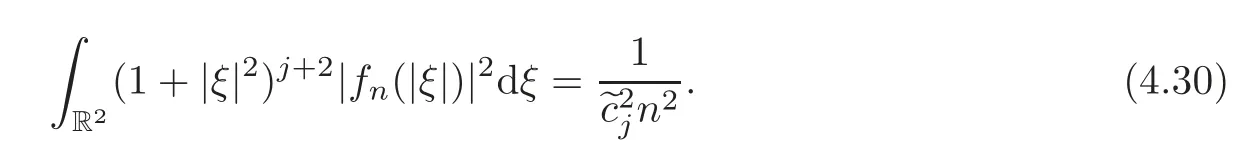
Now,we can apply Theorem 3.3 withf=fn,R1=β1andR2=β2to find that(ηn(t),un(t),pn(t))∈Hj(Ω)solves the problem(1.5)–(1.7).It follows thus from(3.51)and(4.30)that(2.3)holds for alln.

Recalling supp(fn)?B(β1,β2)andλ(|ξ|)≥λ0,we have,after a straightforward calculation and using(3.36)and(4.29),that

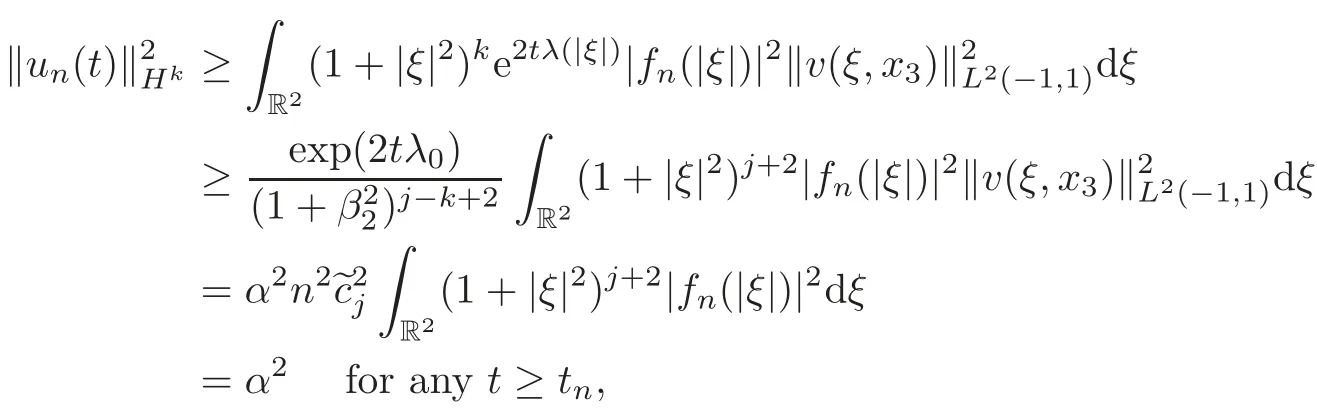
which implies(2.4)–(2.5).This completes the proof of Theorem 2.1

5 Proof of Theorem 2.2

In this section,we will argue by contradiction to show Theorem 2.2.Therefore,we suppose that the perturbed problem has the global stability of orderkfor somek≥3.

5.1 Regularity under the assumption of the global stability

Letδ,C2＞0 andF:[0,δ]→R+be the constants and the function provided by the global stability of orderk,respectively.Lettingn∈N and applying Theorem 2.1 with thisn,k≥3,andα=2,we letsolve(1.5),such that

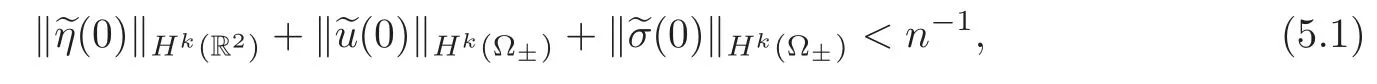
but

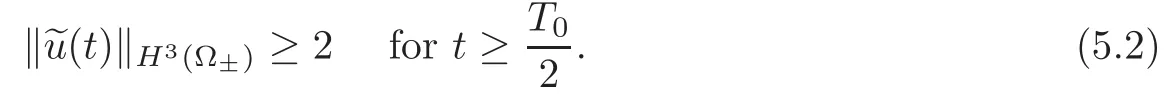
By the Sobolev embedding theorem,Employing the Stein extension theorem,there exist two linear operatorsE+andE?which mapHk(Ω+)andHk(Ω?)toHk(R3),respectively,such that

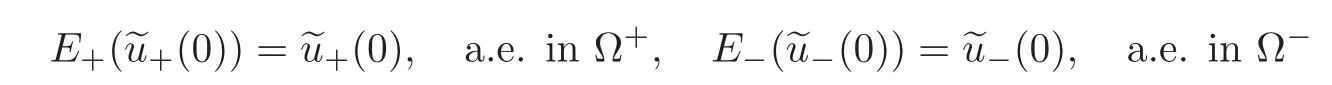
and

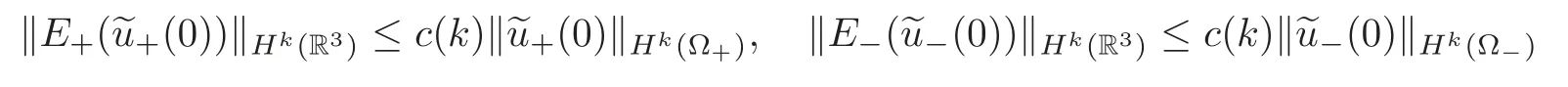
for some constantc(k)depending onk.Keeping in mind thatwe can apply the embedding theorem to see that there exists a suffciently small constantε0＞0,such thatfor anyε∈(0,ε0).Thus,we define

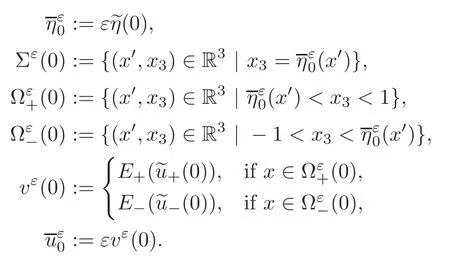
Now,we fixn∈N so thatn＞max{1,C2}max{1,c(k)}.By construction,Moreover,forε＜:=min{ε0,δn(max{1,c(k)})?1},we have

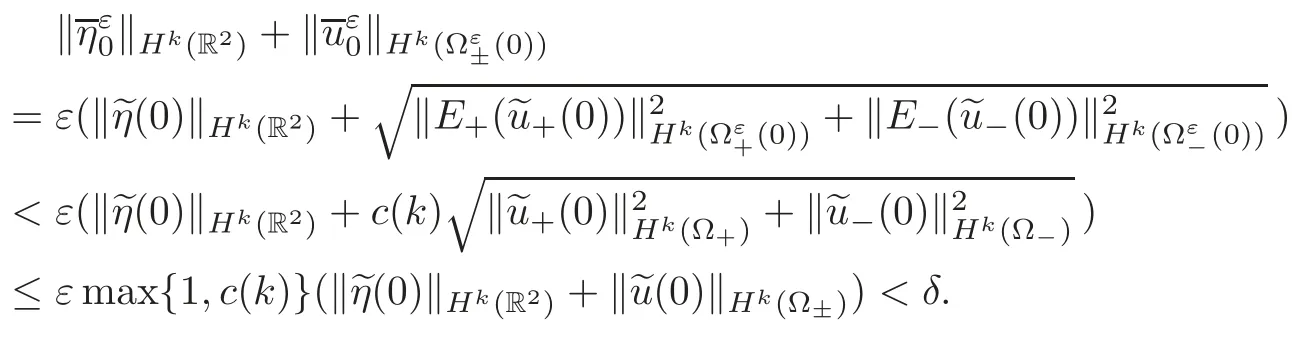
Thus,according to the global stability of orderk,there existηε,uε,σεin the function class described in Definition 2.1,which solve the perturbed problem

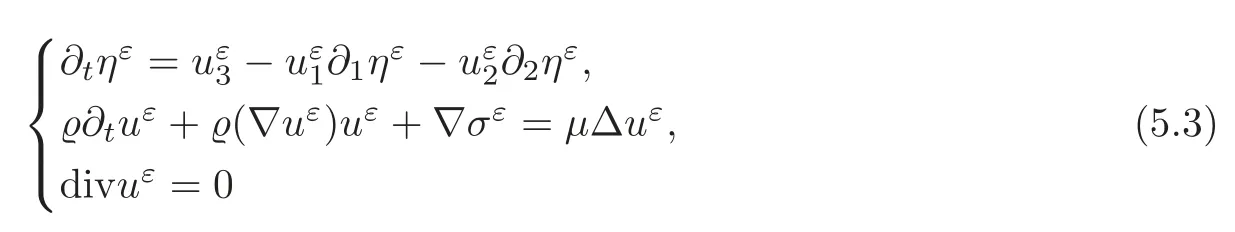
with the jump condition

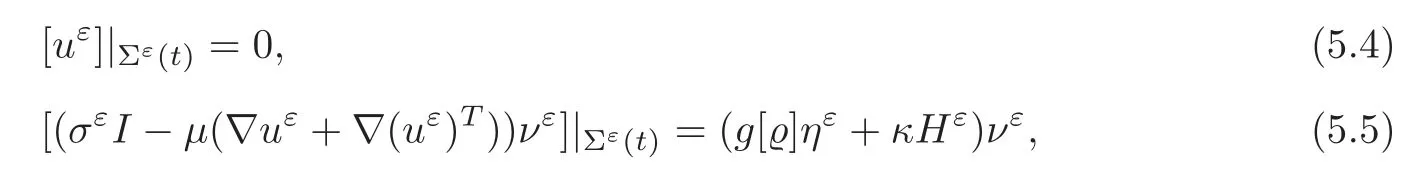
where

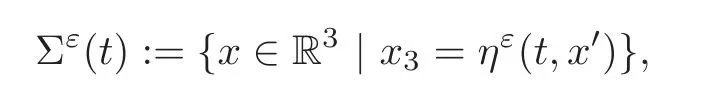
and the initial data satisfyingFurthermore,the solution satisfies

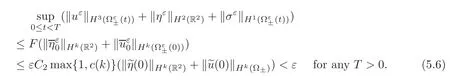
Now,define the rescaled functionsIf we rescale(5.6),then we see that

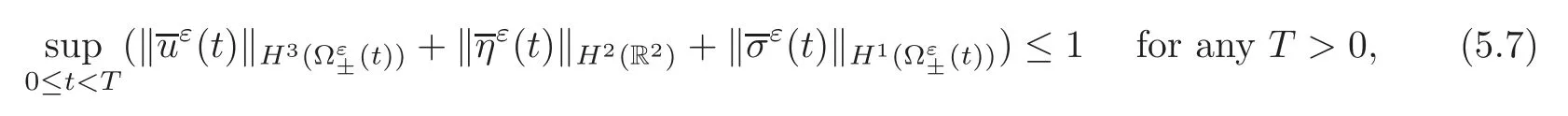
where

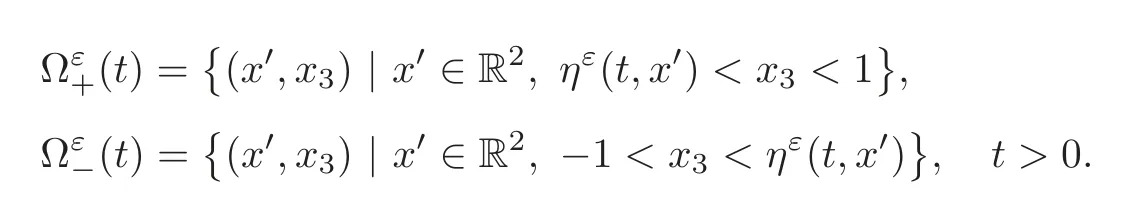
Moreover,recalling the definition ofin(2.2),and using(5.4)and the regularity of(t)in(5.7),we can easily verify that

The second equation in(5.3),together with(5.7),yields

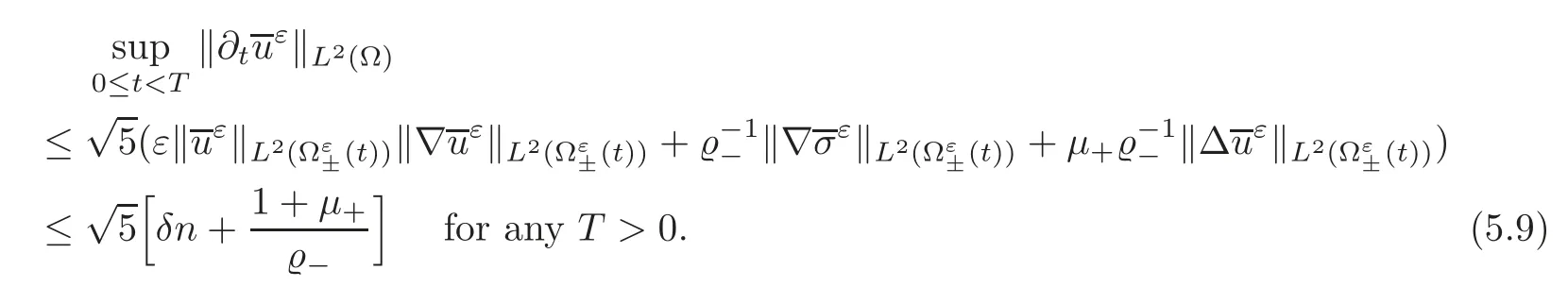
Now,lettingj∈Z+,and employing the first equation of(5.3),(5.7)–(5.8),we infer that for each square domain

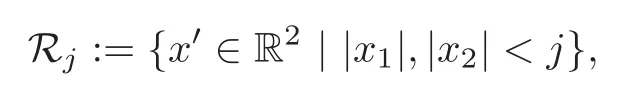
there exists a constantc1(j)depending onj,such that

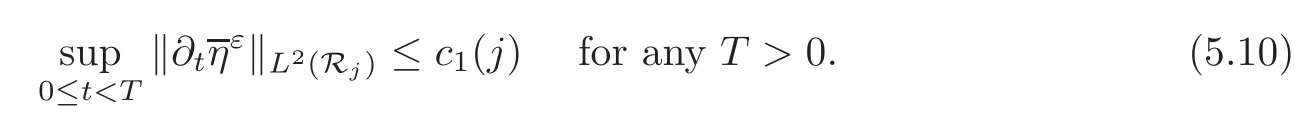
5.2 Taking limits in the rescaled function sequences

First,making use of(5.7)–(5.10),an abstract version of the Arzela-Ascoli theorem(see[16,Theorem 1.70]),and the Aubin-Lions Theorem(see[16,Theorem 1.71]),we can extract a subsequencewithsuch that,for anyp≥1 andj∈Z+,

Hereafter,for simplicity we denotefεmbyfm,wherefrepresentsΣ,orη,and so on.

Denoting

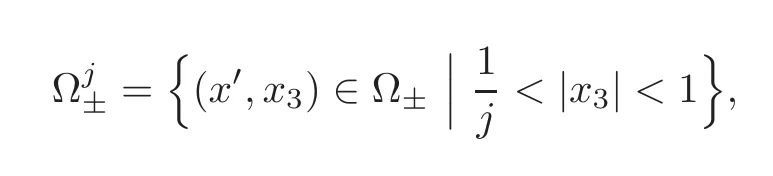
and using the regularity ofηεin(5.6)and the Sobolev embedding theorem,we find that for any positive integerj,there exists anεmj＞0 depending onj,such that,for anyεm∈(0,εmj)andt≥0,we have

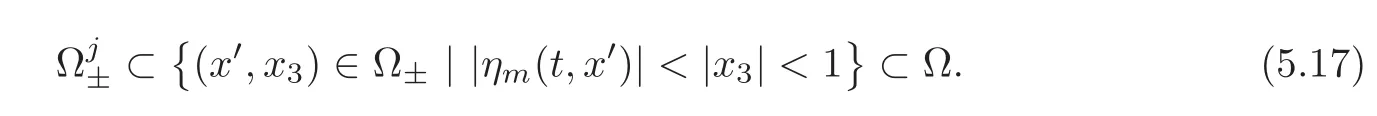
Therefore,for anyj,making use of(5.7),(5.9),(5.17)and the Lions-Aubin Lemma,we can show by induction that there existssuch that

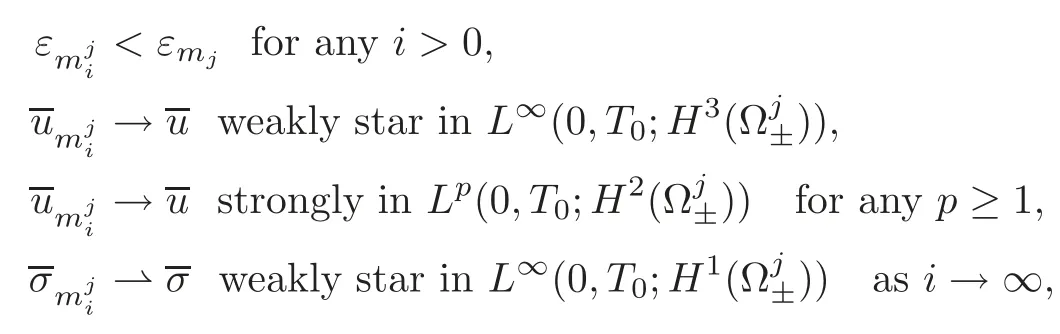
where we have defined

From the lower semicontinuity,one gets

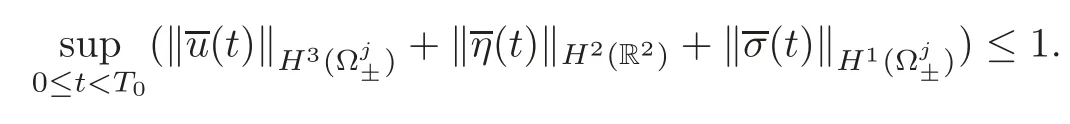
Choosingone has,for anyj∈N andi＞j,that

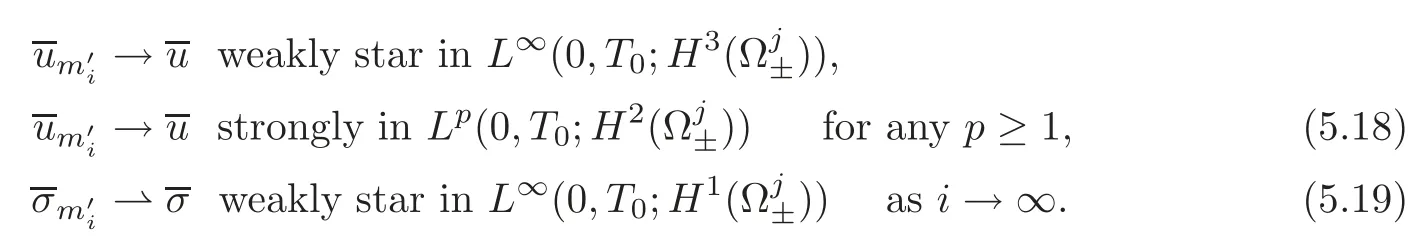
Moreover,by(5.13)and(5.18)–(5.19),we find that

hold a.e.in(0,T0)×(Ω{x3=0}),and

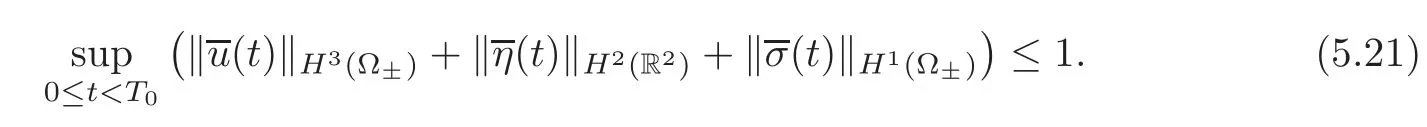
In addition,by construction,we have

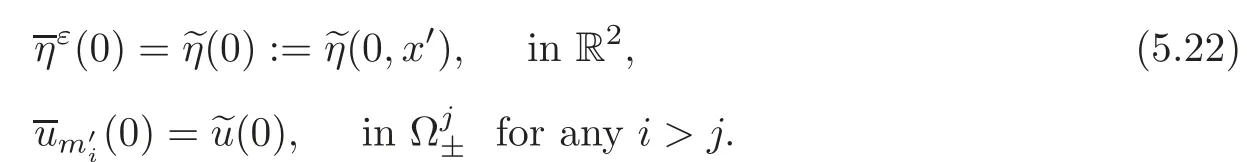
The estimates(5.20)and(5.22),combined with(5.12)and(5.15),imply

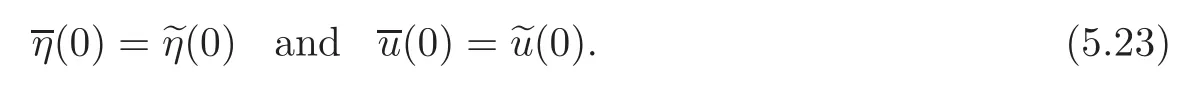
5.3 Convergence of the interface equation

Replacingεbyεm,we rewrite the first equation in(5.3)as

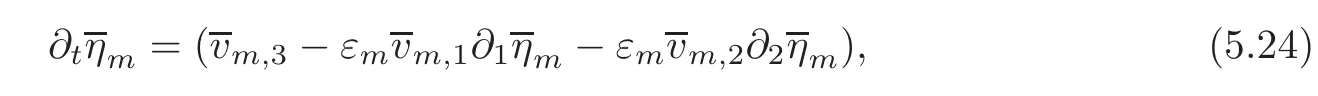
where

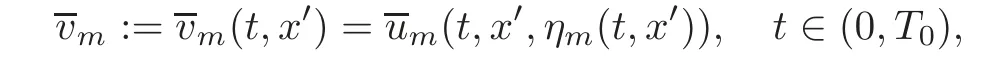
anddenote the fi rst and second components of the vector function,respectively.

Multiplying(5.24)with?∈D(R2)and integrating over R2,then we arrive at

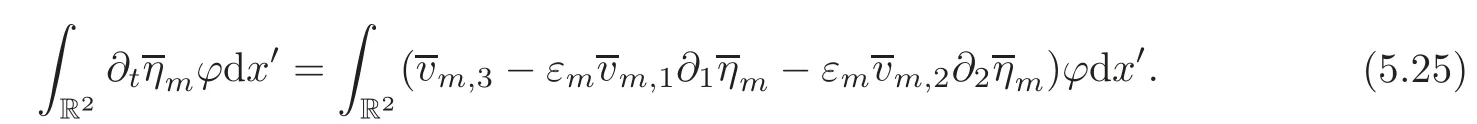
Recallingwe use(5.22)and(5.25)to deduce that

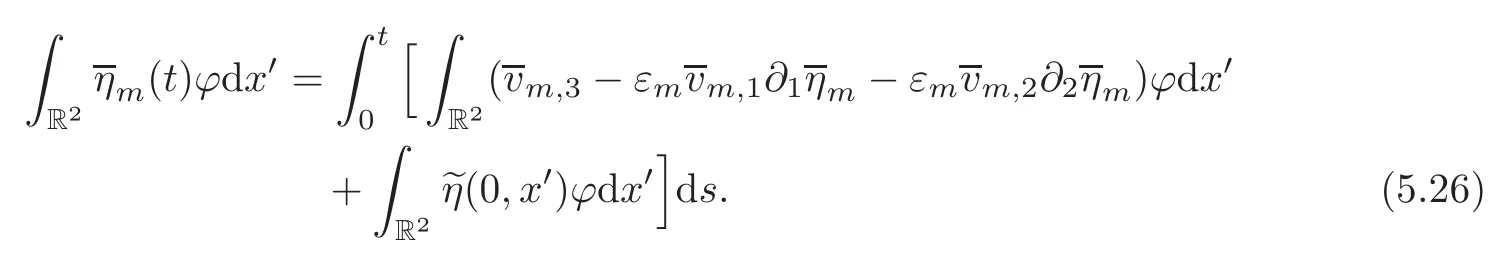
Next,we analyze the convergence of each integral in(5.26).

First,there exists a square domainRj1satisfying

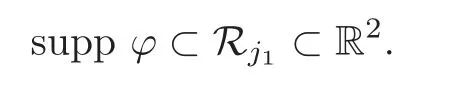
Due to(5.15),we get

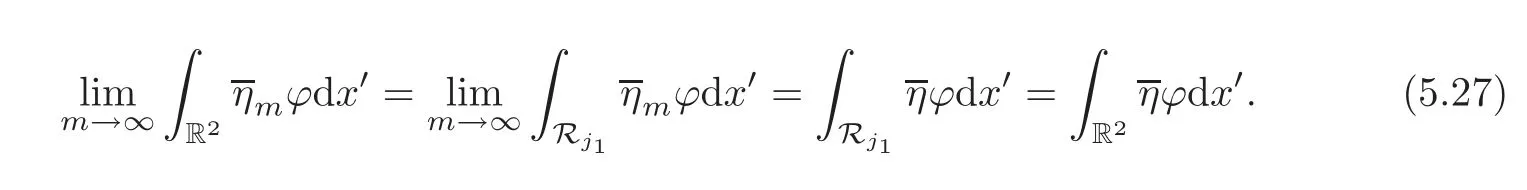
Then,from(5.7),we get

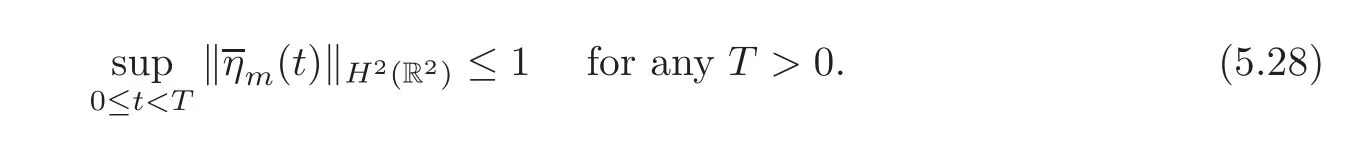
Noticing thatfort＞0,we utilize the H?lder inequality,(5.8)and(5.28)to obtain

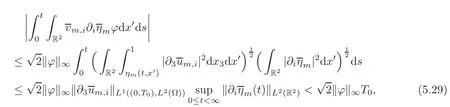
wherei=1,2,and

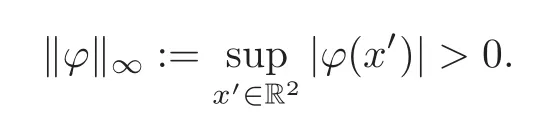
Hence,from(5.29)it follows that

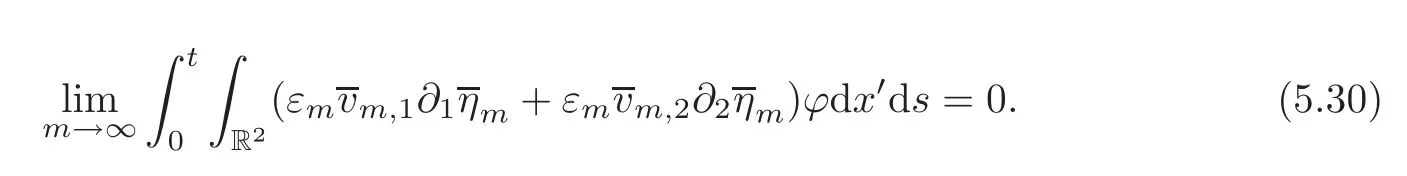
Finally,keeping in mind thatwe use(5.8),(5.18)and the absolute continuity of integrals to deduce that for anyδ＞0,there exists aj2＞j1＞0 depending onj1,T0and‖?‖∞,such that,for anyi＞j2,

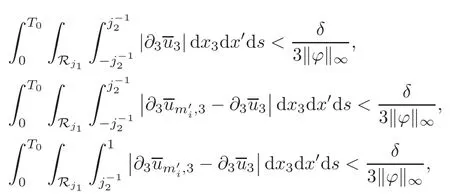
which,recallingby the construction ofand(5.17),imply

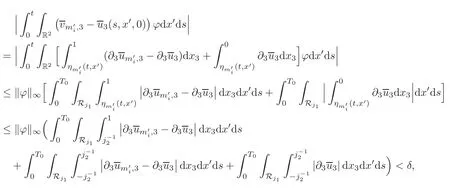
whence

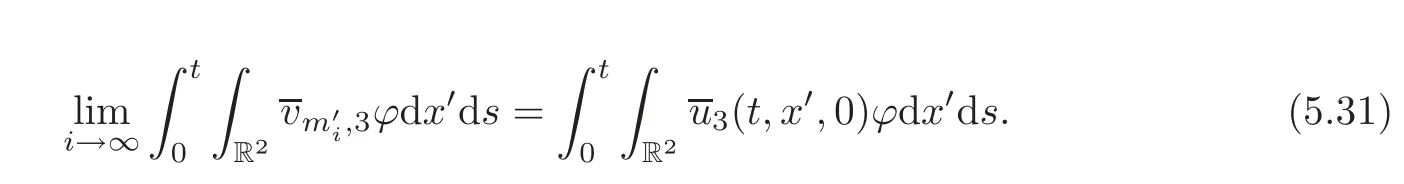
Consequently,lettingi→∞,thenin(5.26)in place ofεm),we conclude,with the help of(5.27)and(5.30)–(5.31),that

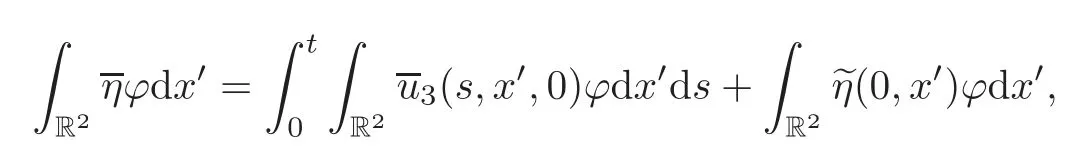
which implies that,for a.e.

5.4 Convergence of the momentum equations

Multiplying the second equation in(5.3)byφ=(φ1,φ2,φ3)∈(D((0,T0)×Ω))3withεmin place ofε,integrating over(0,T0)×Ω,and using the jump conditions(5.5),we deduce

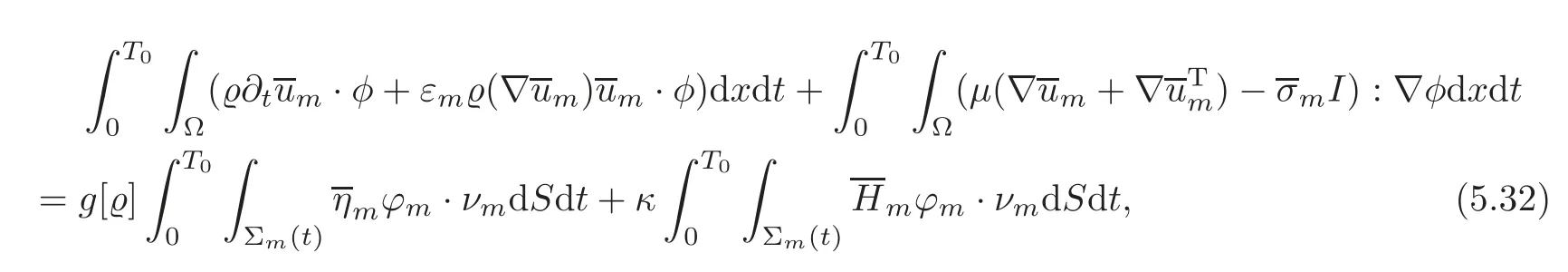
where

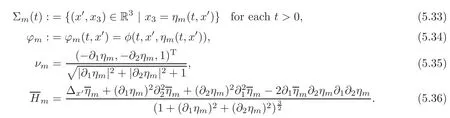
By virtue of(5.11)–(5.13)and(5.16),

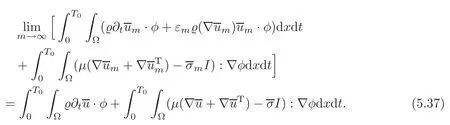
Next,we analyze the convergence of the terms on the right-hand side of(5.32).

(i)Recallingwe use the formula of surface integral and(5.33)–(5.35)to infer that

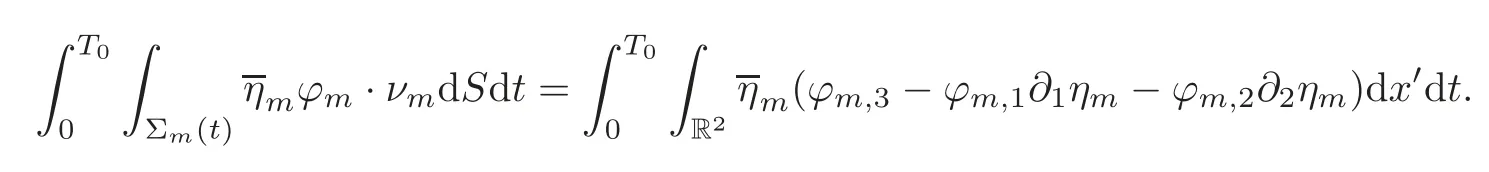
Now we define

thus,from the Hlder inequality and(5.28),it follows that

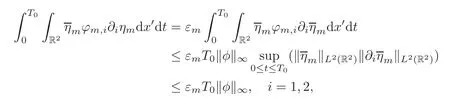
whence

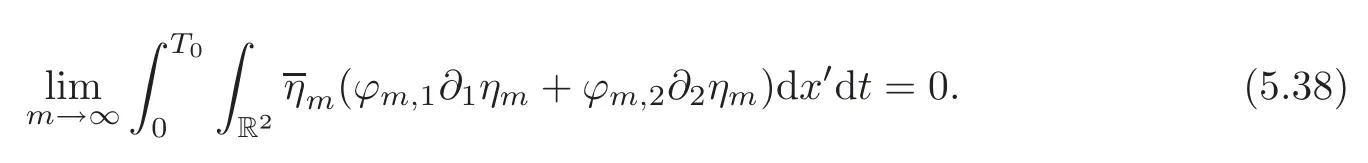
Noticing that

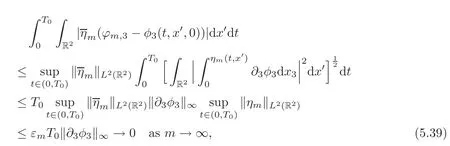
we make use of(5.15)and(5.39)to obtain

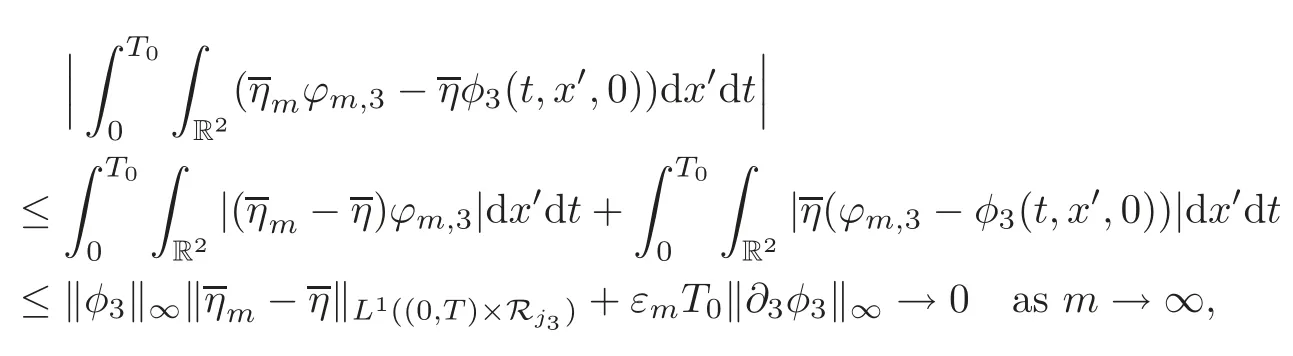
which gives

Here we have assumed thatRj3satisfies

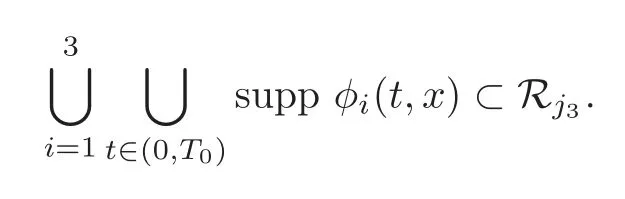
Combining(5.38)with(5.40),we arrive at

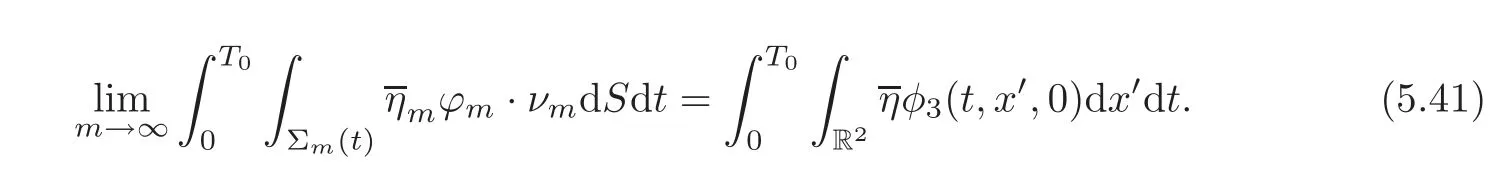
(ii)For the second term on the right-hand side of(5.32),taking into account thatwe employ(5.33)–(5.36)to deduce that

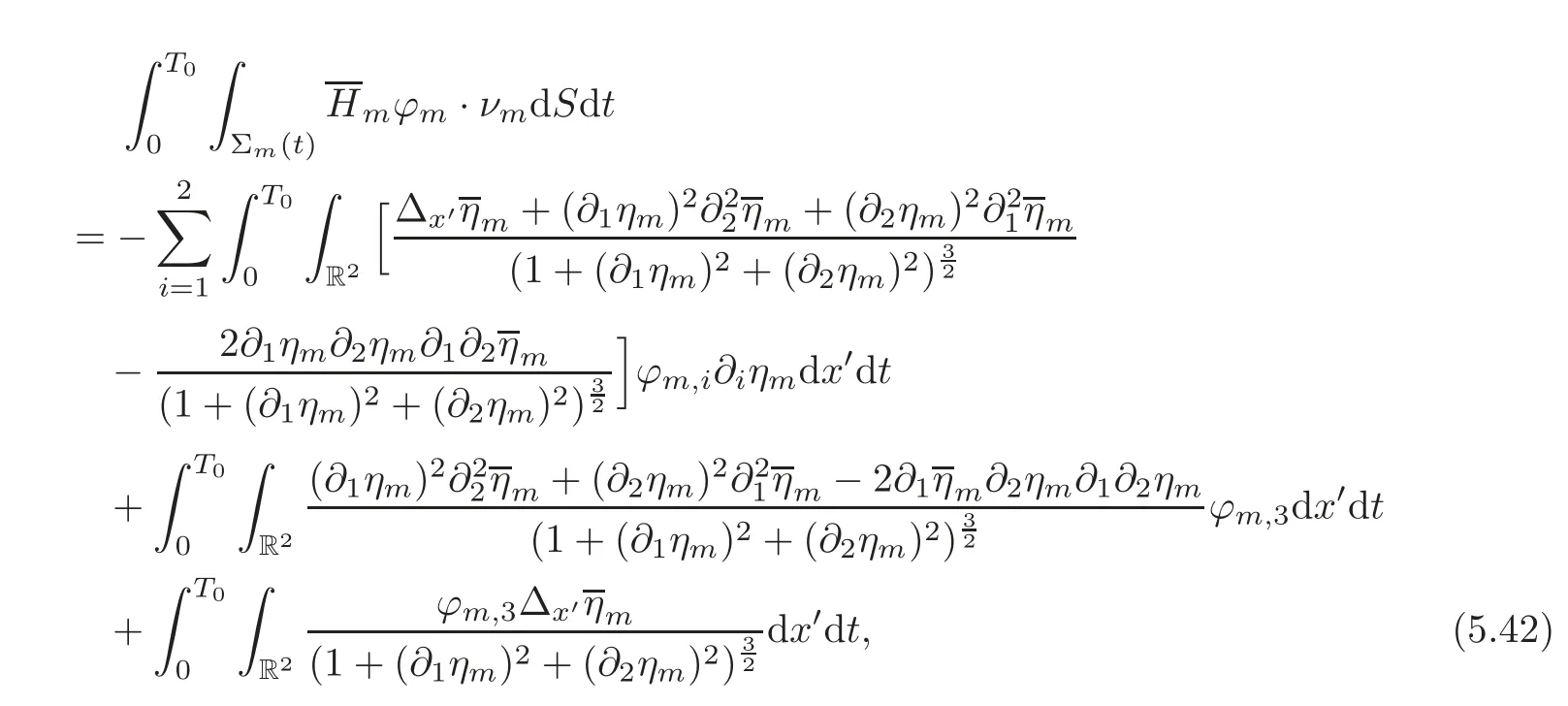
where the first two terms on the right-hand side can be estimated as follows,using the Sobolev imbedding theorem and(5.28),while the third term can be bounded below,following a procedure similar to that used for(5.39):

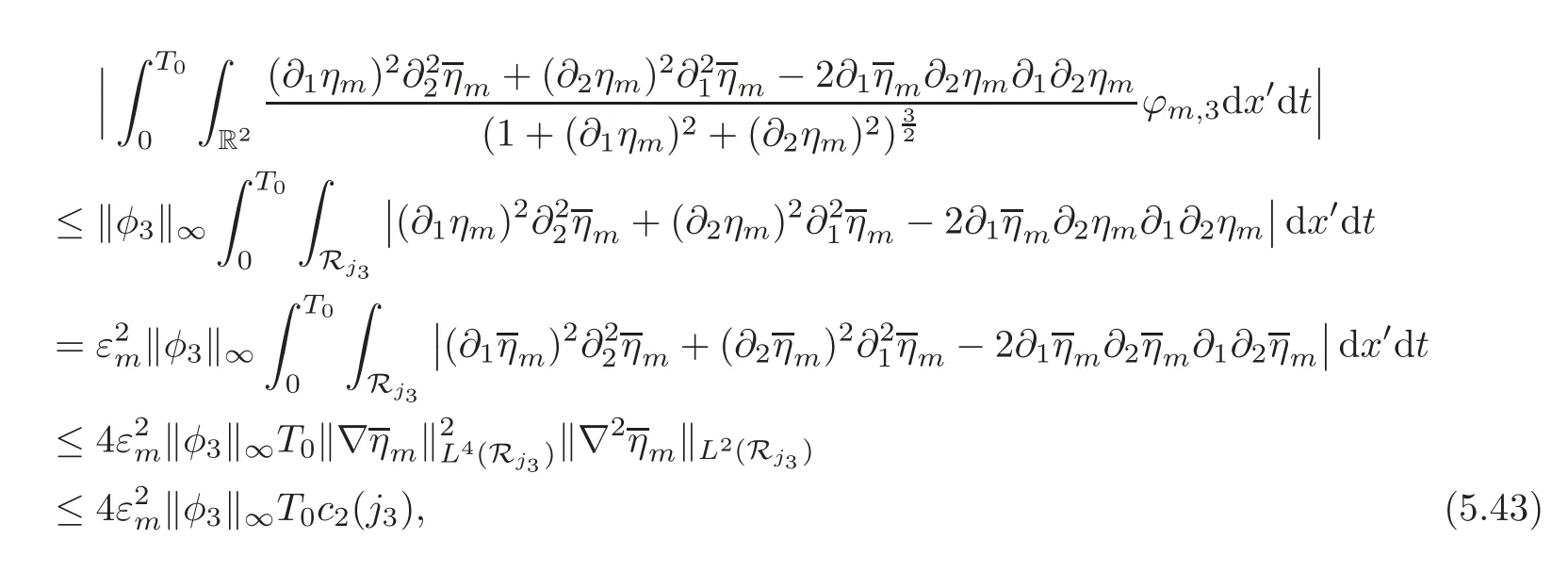
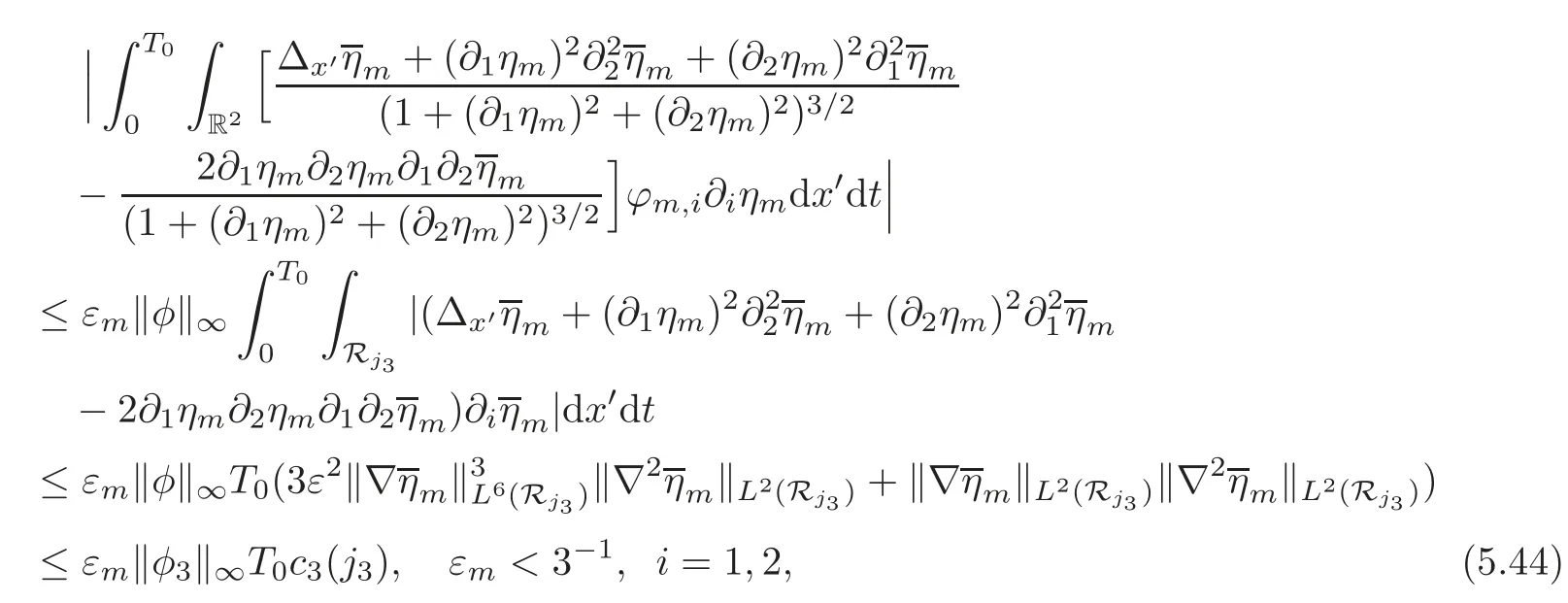
wherec2(j3)andc3(j3)are two constants depending onj3,and

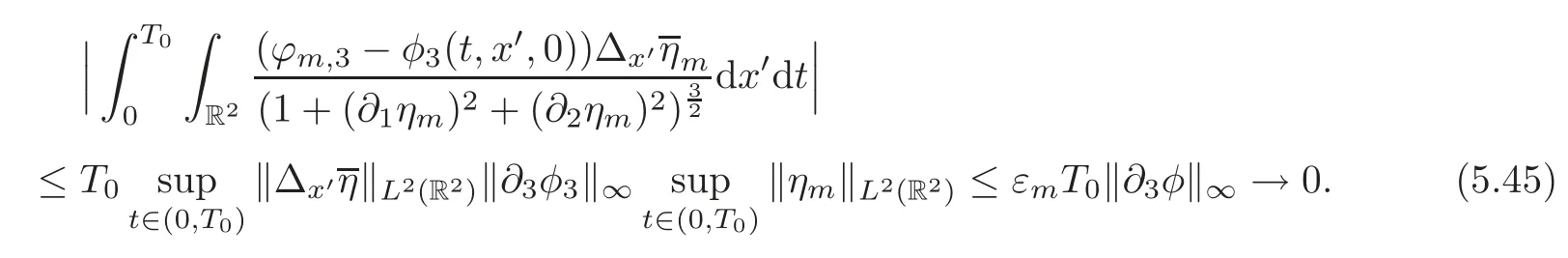
On the other hand,applying(5.15)and the dominated convergence theorem,we conclude that

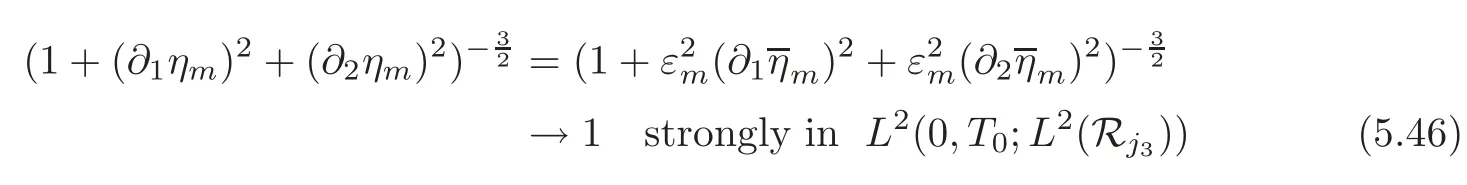
asm→ ∞,whileεm→0.Thus,from(5.46)and(5.14),we get

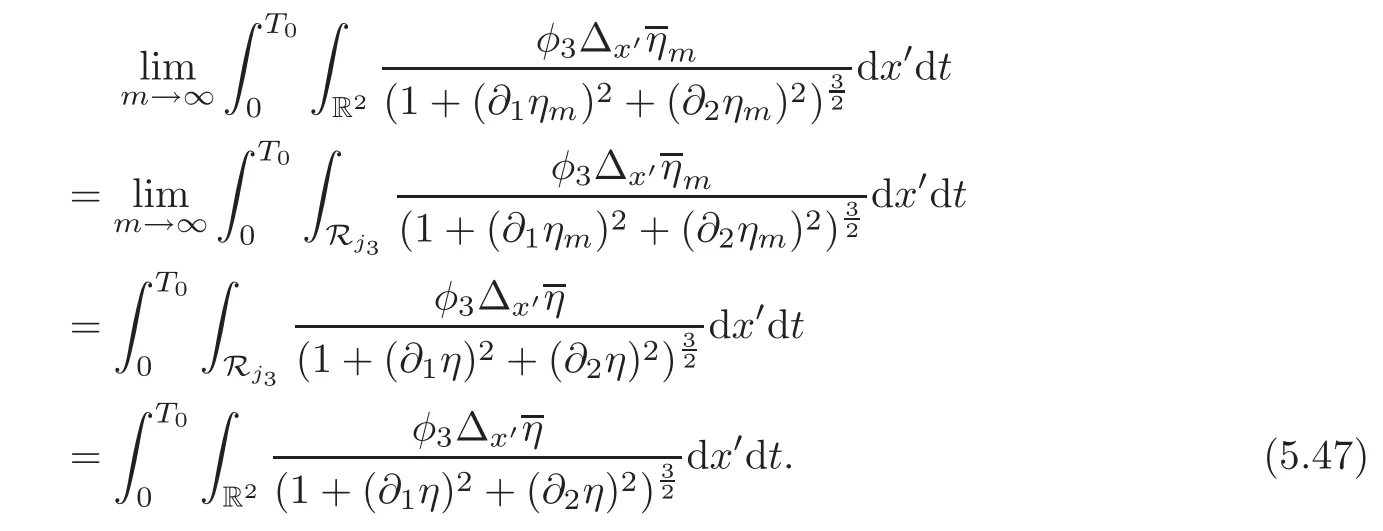
In view of(5.45)and(5.47),we find that

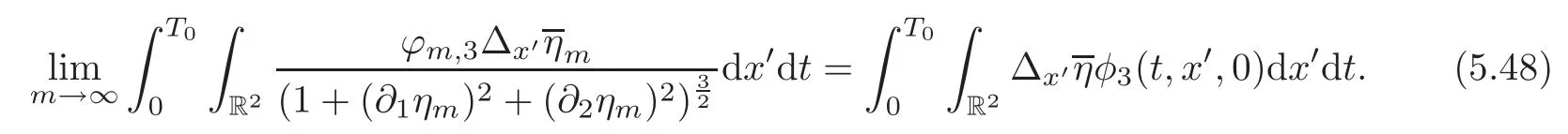
Combining(5.43)with(5.44)and(5.48),we conclude that

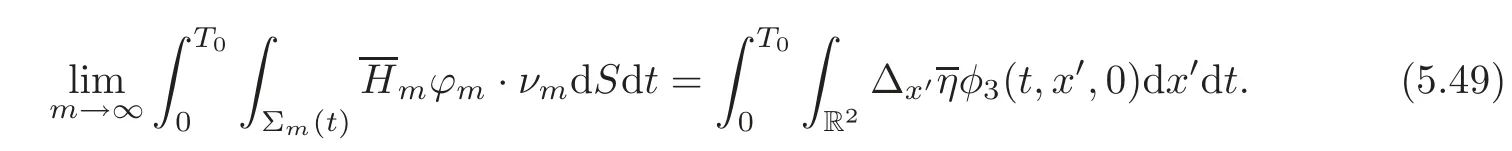
Consequently,it follows from(5.32),(5.37),(5.41)and(5.49)that

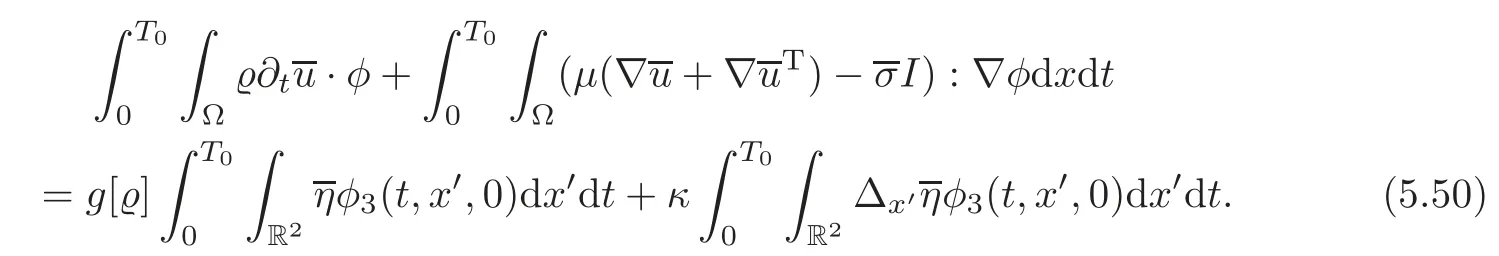
5.5 Contradiction argument

In a way similar to(4.18),we multiply the first equation in(5.20)withφ∈(D((0,T0)×Ω))3and integrate over(0,T0)×Ω to infer that

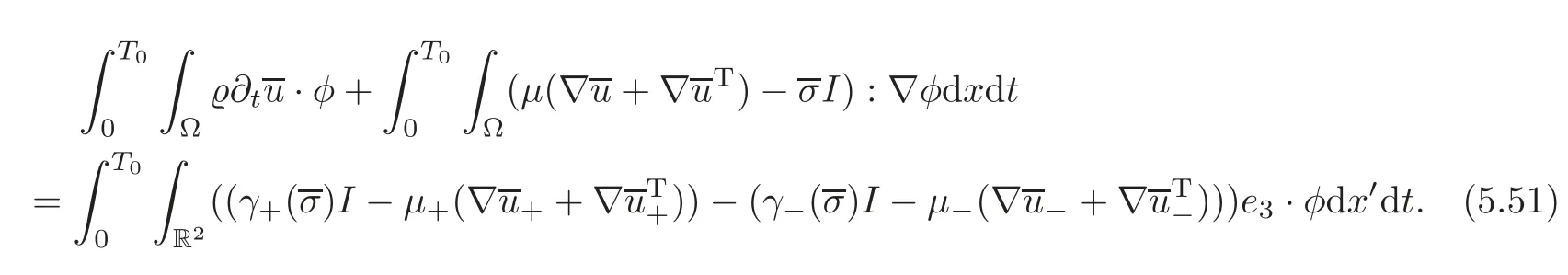
Comparing(5.51)with(5.50),we get

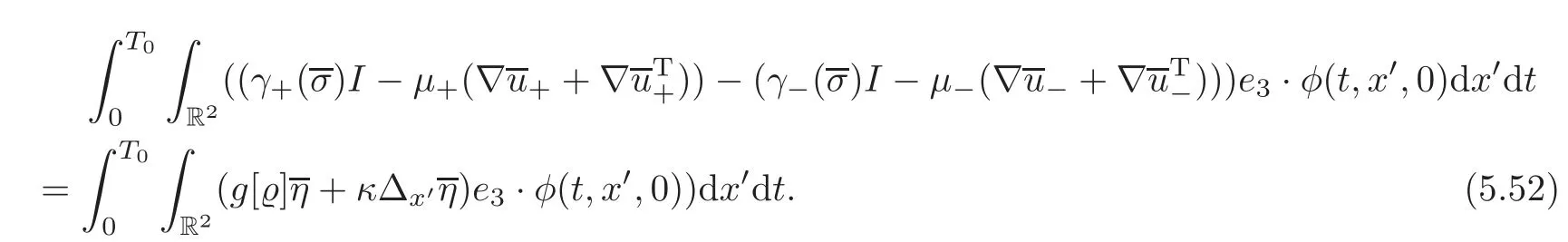
On the other hand,by Lemma 4.1,(4.11),(5.11)and(5.21),we have

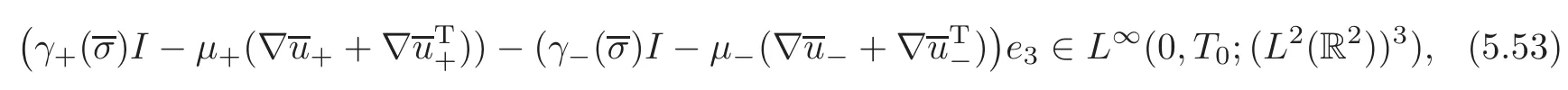
while by virtue of(5.28),

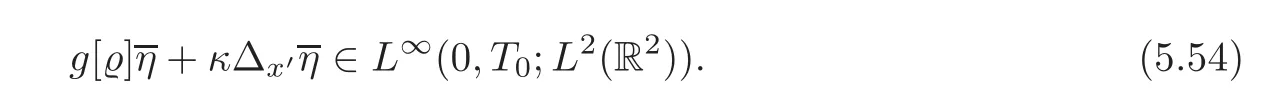
Hence,by a density argument,we get from(5.52)–(5.54)that

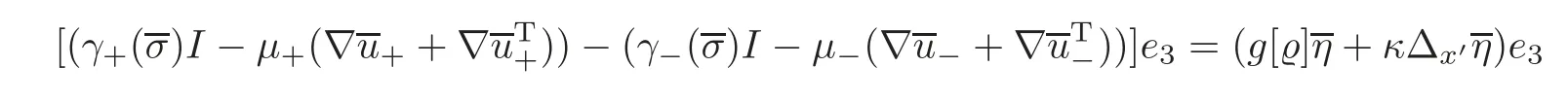
holds a.e.in R2and for a.e.t∈(0,T0).

In view of Definition 4.1,we find thatis just a strong solution to the linearized problem(1.5)–(1.7).By Remark 4.2,is also a strong solution to(1.5)–(1.7).Moreover,and(see(5.23)).Then,according to Theorem 4.1,

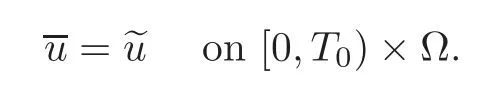
Hence,we may chain together the inequalities(5.2)and(5.21)to get

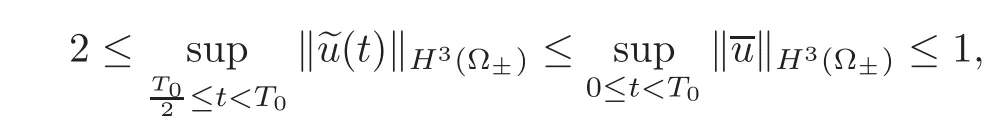
which is a contradiction.Therefore,the perturbed problem does not have the global stability of orderkfor anyk≥3.This completes the proof of Theorem 2.2.

AcknowledgementThe authors are grateful to the referees for their comments which are helpful in improving the presentation of this paper.

[1]Adams,R.A.and John,J.,Sobolev Space,Academic Press,New York,2005.

[2]Chandrasekhar,S.,Hydrodynamic and Hydromagnetic Stability,The International Series of Monographs on Physics,Clarendon Press,Oxford,1961.

[3]Duan,R.,Jiang,F.and Jiang,S.,On the Rayleigh-Taylor instability for incompressible,inviscid magnetohydrodynamic flows,SIAM J.Appl.Math.,71,2011,1990-2013.

[4]Ebin,D.,The equations of motion of a perfect fluid with free boundary are not well-posed,Comm.Part.Diff.Eq.,12,1987,1175–1201.

[5]Ebin,D.,Ill-posedness of the Rayleigh-Taylor and Helmholtz problems for incompressible fluids,Comm.Part.Diff.Eq.,13,1988,1265–1295.

[6]Guo,Y.and Tice,I.,Compressible,inviscid Rayleigh-Taylor instability,Indiana Univ.Math.J.,60,2011,677–712.

[7]Guo,Y.and Tice,I.,Decay of viscous surface waves without surface tension,2010.arXiv:1011.5179v1

[8]Guo,Y.and Tice,I.,Linear Rayleigh-Taylor instability for viscous,compressible fluids,SIAM J.Math.Anal.,42,2011,1688–1720.

[9]Hwang,H.J.,Variational approach to nonlinear gravity-driven instability in an MHD setting,Quart.Appl.Math.,66,2008,303–324.

[10]Hwang,H.J.and Guo,Y.,On the dynamical Rayleigh-Taylor instability,Arch.Rational Mech.Anal.,167,2003,235–253.

[11]Jiang,F.,Jiang,S.and Ni,G.X.,Nonlinear instability for nonhomogeneous incompressible viscous fluids,Sci.China Math.56,2013,665–686.

[12]Jiang,F.,Jiang,S.and Wang,Y.J.,On the Rayleigh-Taylor instability for incompressible viscous magnetohydrodynamic equations,Commun.Part.Diff.Eq.,39,2014,399–438.

[13]Jiang,F.,Jiang,S.and Wang,W.W.,Nonlinear Rayleigh-Taylor instability in nonhomogeneous incompressible viscous magnetohydrodynamic fluids,2013.arXiv:1304.5636

[14]Kruskal,M.and Schwarzschild,M.Some instabilities of a completely ionized plasma,Proc.Roy.Soc.(London)A,233,1954,348–360.

[15]Nespoli,G.and Salvi,R.,On the existence of two-phase problem for incompressible flow,Advances in Fluid Dynamics,Quaderni di Mathematica,4,P.Maremonti(ed.),Dept.Math.,Seconda Univ.,Napoli,1999,245–268.

[16]Novotny,A.and Stra?kraba,I.,Introduction to the Mathematical Theory of Compressible Flow,Oxford University Press,Oxford,2004.

[17]Prüess,J.and Simonett,G.,On the Rayleigh–Taylor instability for the two-phase Navier–Stokes equations,Indiana Univ.Math.J.,59,2010,1853–1871.

[18]Rayleigh,L.,Analytic solutions of the Rayleigh equations for linear density profiles,Proc.London.Math.Soc.,14,1883,170–177.

[19]Rayleigh,L.,Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density,Scientific Paper,II,1990,200–207.

[20]Taylor,G.I.,The stability of liquid surface when accelerated in a direction perpendicular to their planes,Proc.Roy Soc.A,201,1950,192–196.

[21]Tice,I.and Wang,Y.J.,The viscous surface-internal wave problem:Nonlinear Rayleigh-Taylor instability,Commun.Part.Diff.Eq.,37,2012,1967–2028.

[22]Wang,J.,Two-Dimensional Nonsteady Flows and Shock Waves(in Chinese),Science Press,Beijing,1994.

[23]Wang,Y.,Critical magnetic number in the MHD Rayleigh-Taylor instability,J.Math.Phys.,53,2012,073701.

[24]Wehausen,J.and Laitone,E.,Surface Waves,Handbuch der Physik,Vol.9,Part 3,Springer-Verlag,Berlin,1960.