Yulai WU Ximin LIU

1 Introduction

LetXbe a compact closed oriented simply connected topological 4-manifold,andGbe a finite group.When studying actions on manifold of a finite group,one can consider an induced action on some algebraic invariants associated with the manifold,and it is often important and benef i cial.Furthermore,a central problem is to describe the structure of the fixed point set(fixed point data,early noted in[7])and the action around it.Various investigations have been conducted under different conditions and cases such as the certain manifold carries a geometric structure,or the group may be fundamental likeG≡Zpfor some primepor other simple cases.One may also see the recent surveys of[3,6].

Moreover,a specific question may be concerned with the homological rigidity that whether an action is trivial if the induced action is trivial on homology.In the case of holomorphic actions,K3 surfaces provide a classical example that every homologically trivial automorphism of aK3 surface is trivial(see[2]).There are no locally linear,homologically trivial involutions on a homotopyK3 surface while a locally linear Zp-action is automatically homologically trivial on a homotopyK3 surface forp＞23 by the decomposition of the integral Zp-representation onH2(K3)(see[15,19]).Peters extended homological rigidity of holomorphic actions to the elliptic surfaces in[18].McCooey[16]established homological rigidity for locally linear topological actions for non-Abelian groups.Edmonds[5]showed that for any primep＞3,there exists a locally linear,pseudofree and homologically trivial topological Zp-action.

For symplectic actions,some recent results have been obtained as well.Chen and Kwasik[4]proved that there are no homologically trivial,symplectic actions of a finite group on the standardK3 surface(with respect to any symplectic structure),partially extending Peters’results in[18]to the symplectic category.

LetX=E(n)be the relatively minimal elliptic surface with rational base,where the elliptic surfaceE(n)is defined as then-fold fiber sum of copies ofE(1),andE(1)isbeing equipped with an elliptic fibration.Note thatE(n)is spin if and only ifnis even.The elliptic surfaceE(n)is known to have many exotic smooth structures,where theE(n)with an exotic smooth structure is also called a homotopy elliptic surface,which is homeomorphic,but not diffeomorphic,to the standard elliptic surface.It is well-known that there are two methods to produce exotic smooth structures onE(n):Logarithmic transformations(see[9])and Fintushel-Stern’s knot surgery construction(see[8]).

In[13–14],Nakamura and the second author studied the locally linear actions on elliptic surfacesE(n)and proved that there exists a locally linear cyclic group action onE(n)which is nonsmoothable with respect to infinitely many smooth structures onE(n).In this paper,some symplectic Zp-actions of prime orders on homotopy elliptic surfacesE(n)are studied.In the meantime,we investigate the symplectic actions on the homotopyE(4)surfaces,and get some rigidity result.Our main results are stated as following.

Theorem 1.1Let G=Zp,and X=E(n)be a homotpy elliptic surface with c21=0and n is even.

(1)For p=3,there is no homologically trivial,pseudofree,symplectic G-action on X.

(2)For p=5,if X admits a symplectic,nontrivial,homologically trivial,pseudofree action of G.Then the fixed point set of the G-action consists of4n fixed points,each withlocal representationand8n fixed points,each with local representationfor some k/=0 mod 5.

Theorem 1.2Let X be the symplectic4-manifold(E(4),ω)with c21=0and c1(K)·[ω]＜16,where ωdef i nes an integral class[ω]∈H2(X;R).Then there are no nontrivial homologically trivial actions of a finite group on X which preserve the symplectic structure ω.

The current paper is organized as follows:In Section 2,we provide some preliminaries and tools.In Section 3,we initiate basic knowledge of Seiberg-Witten theory from Taubes,and restate the results of Chen and Kwasik about the structures of the union of finitely manyJ-holomorphic curvesand the fixed point setFunder the symplectic actions.Then we give the proof of the main results of this paper in Section 4.At last,some calculation results and the mean contributions to theg-signature theorem are introduced in Section 5 as an appendix.

2 Preliminaries and Tools

In this section,we collect some results about Lefschetz fixed point theorem andg-signature theorem which we will use as the main tools(see[1,10–11]).

LetXbe a closed,oriented smooth 4-manifold,and let cyclic groupG≡Zpof prime order act onXeffectively via orientation-preserving diffeomorphisms.Then the fixed point setF=XG,if nonempty,will consists of isolated points and surfaces.If a generatorgofGis fixed,each fixed pointm∈Fis associated with a nonzero integers pair(am,bm),where?p＜am,bm＜p,and they are uniquely determined up to a change of order or a change of sign simultaneously,such that the inducedg-action on the tangent space atmis given by the complex linear transformationwhereFor each connected surfaceY?F,the action ofgon the normal bundle ofYinXis given byfor an integercYwith 0＜cY＜p,which is uniquely determined up to a sign modulop.The following is the Lefschetz fixed point theorem.

Theorem 2.1(Lefschetz Fixed Point Theorem)Let T:X→X generate an action ofZpon X,a closed,simply-connected4-manifold.Then L(T,X)=χ(F),where χ(F)is the Euler characteristic of the fixed point set F and L(T,X)is the Lefschetz number of the map T,which is defined by

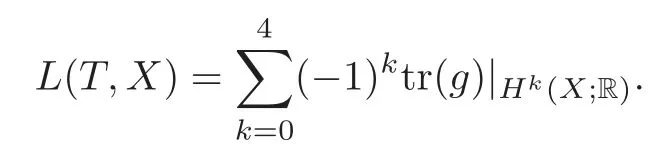
Theorem 2.2(G-signature Theorem)Setting

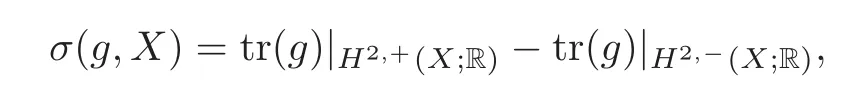
then

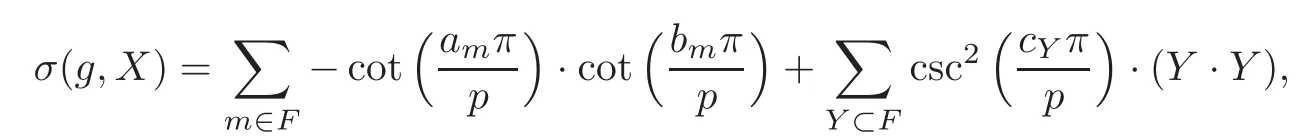
where Y·Y denotes the self-intersection number of Y.

The weaker version of theG-signature theorem is used more often since the convenient for calculation.

Theorem 2.3(G-signature Theorem-the Weaker Version)

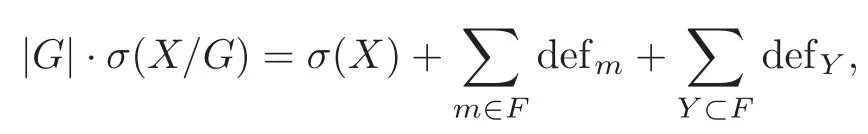
where the termsdefmanddefYare called signature defects.They are given by the following formulae:

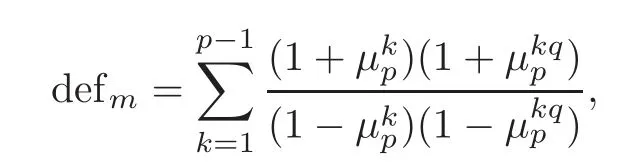
if the local representation of G at m is given byand

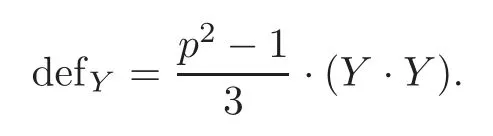
3 Symplectic Zp-Actions on 4-Manifolds with=0

In this section,we restate the results by Chen and Kwasik[4]in a clear way to lay a foundation of the proof to main results of this paper.We shall brief l y initiate with theG-equivariant Seigberg-Witten-Taubes theory,for more details one may see[20–21].

LetXbe a 4-manifold equipped a symplectic structureωwith aG≡Zpaction via symplectomorphisms on it.IfXis minimal with=0 and≥2,and the induced action onH2(M;Q)is trivial,then,according to Taubes’results in[20–21],for anyG-equivariantω-compatible almost structureJ,there exists a solution(A,ψ)to theG-equivariant Seiberg-Witten equations

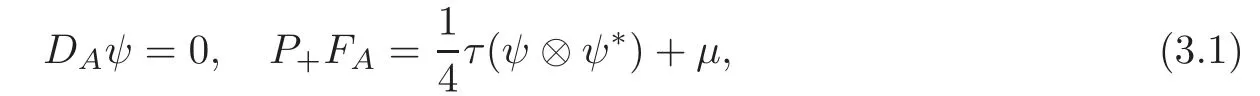
with perturbation termfor anyr＞0.HereAis aG-equivariantU(1)-connection andψ∈Γ(S+)is aG-equivariant smooth section ofS+.S+andS?are associatedU(2)vectorG-bundles.DA:Γ(S+)→Γ(S?)is the Dirac operator.P+is the orthogonal projection.

Denotingthe zero locusα?1(0),if nonempty,will pointwise converge to a union of finitely manyJ-holomorphic curves with multiplicity representing the Poincare dual ofc1(K)asr→+∞.We denote the union of theJ-holomorphic curves asfor finitely manyi,and categorize the componentsas the following three types.

(A){Λα}is either an embedded torus,or a nodal sphere,or a cusp sphere,all with selfintersection 0.

(B){Λα}is a union of two embedded(?2)-spheres intersecting at a single point with tangency of order 2.

(C){Λα}is a union of embedded(?2)-spheres intersecting transversely.

If each sphereCi?Λαcorresponds to a vertexviand each intersection point ofCi∩Cjcorresponds to an edge connectingviandvj,then the union of intersecting spheres can be represented by a graph.Moreover,we can associate a positive semi-definite matrixQα=(qij),whereandCi·Cj/=0 andqij=0 fori/=jandCi·Cj=0,noting that we assume=0 in the main theorem implies that the annihilator exists for Lemma 2.10 in[2].By Lemma 2.12(ii)of[2],the graph must be one of the figures(with weights)listed as follows.

The cases about the structures ofand the fixed point setFare as follows:

(1)Isolated fixed points not contained inwith local representations

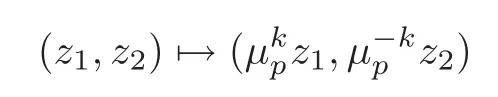
for somek≠0 modp,i.e.,with local representations contained inSL2(C).

(2)The connected components Λαofmay include:

(I)A torus with self-intersection 0,if not entirely fixed byG,contributing four isolated fixed points all with same local representationfor somek≠0 modpwhenp=2,or three isolated fixed points all with same local representationorfor somek≠0 modpwhenp=3,toXG.

(II)A cusp sphere with self-intersection 0,contributing two isolated fixed points toXGonly whenp≥5,one of which is the cusp singularity with local representation(z1,z2)for somek≠0 modp,while the other with local representation(z1,z2)for somek≠0 modp.

(III)A nodal sphere with self-intersection 0,contributing one fixed point as the double point with local representationfor somek≠0 modp.

(IV)Two(?2)-spheres intersecting at a point with order 2,contributing the intersection point toXGwith local representationfor somek≠0 modpifp=3,orfor somek≠0 modpifp＞3.

(V)A union of embedded(?2)-spheres intersecting transversely with each other.

(i)Λαcontains a 2-dimensional component ofF,withn=4 modpif Λαis represented by a typegraph andn=?1 modpif Λαis represented by a typegraph.

(ii)Λαis of typeand the intersection of each pair of spheres is an isolated fixed point,with rotation numbers(1,p?1)associated to either sphere.

(iii)Λαis of typewhere the three spheres intersect at a single point;there are four isolated fixed points,one occurs at the intersection point and each of the other three is contained in each one of the three spheres,with the rotation numbers associated to each sphere being(1,1)at the intersection point and(1,|p?3|)at each of the other three fixed points.This case occurs only ifp/=3.

(iv)Λαis of typewhich contains four isolated fixed points.The rotation number at each fixed point is(1,1),and this case occurs only ifp=2.

The structure of the fixed point set for a symplectic cyclic action of prime order on a minimal symplectic 4-manifoldXwith=0 and≥2,which induces a trival action onH2(X;Q),was described by Chen and Kwasik in[4].We invoke the result for the case of pseudofree actions below.

Theorem 3.1(see[4])Let X be a minimal symplectic4-manifold withwhich admits a nontrival,pseudofree action of G=Zp,where p is a prime,such that the symplectic structure is preserved under the action and the induced action on H2(X;Q)is trivial.Then the set of fixed points of G can be divided into groups,each of which belongs to the followingfive possible types:

(1)One fixed point with local representationfor some k≠0 modp,i.e.,with representation contained in SL2(C).

(2)Two fixed points with local representation

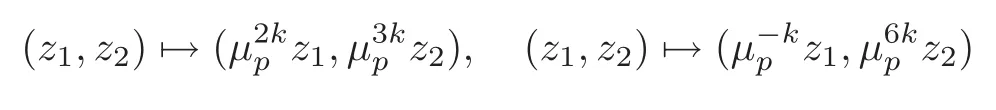
for some k≠0 modp,respectively.This type of fixed points occurs only when p＞5.

(3)Three fixed points,one with local representationand the othertwo with local representationfor some k≠0 modp.This type offixed points occurs only when p＞3.

(4)Four fixed points,one with local representationand the otherthree with local representationfor some k≠0 modp.This type offixed points occurs only when p＞3.

(5)Three fixed points,each with local representationfor some k≠0 modp.This type of fixed points occurs only when p=3.

The rigidity for the corresponding homologically trivial actions is as follows,and it shows that symplectic symmetries are more restrictive than topological ones.

Theorem 3.2(see[4])Let X be a minimal symplectic4-manifold with=0and≥2,which admits a homologically trivial(overQcoeffcients),pseudofree,symplecticZp-action for a prime p.Then the following conclusions hold:

(a)The action is trivial if p≠1 mod 4,p≠1 mod 6,and the signature of X is nonzero,then for infinitely many primes p the manifold X does not admit any such nontrivialZp-actions.

(b)The action is trivial as long as there exists a fixed point of type(1)in Theorem3.1.

4 Proofs of the Main Results

Proof of Theorem 1.1(1)First consider the Z3-case.The fixed points of a pseudofree Z3-action onXcan be divided into two types by considering their local representation:

The type(+):(1,2)or(2,1).

The type(?):(1,1)or(2,2).

Letk+,k?be the numbers of the fixed points of the type(+),type(?)in the fixed point set separately.Letmandnbe one fixed point of type(1,1)and(1,2),respectively.Then defThe formula in Theorem 2.3 is rewritten as

Together with the Lefschetz fixed point theorem,we have the following inequality:

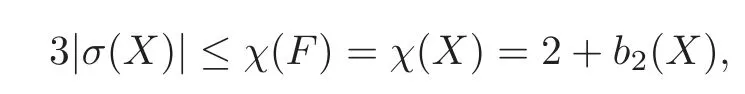
or

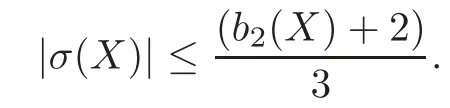
Obviously,the elliptic surfaces do not satisfy that.

(2)By the assumption that theG-action onX=E(n)is pseudofree and with theG-signature theorem,we have

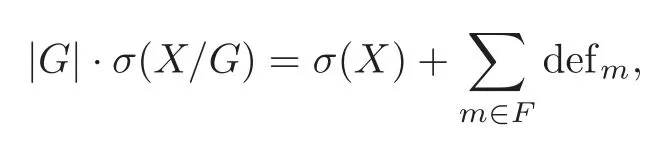
whereG=Z5,andF=XGdenotes the fixed point set.

The induced action onH2(X;Q)is trivial.Thenσ(X/G)=σ(X)and the Lefschetz fixed point theorem leads toχ(F)=χ(X).The fixed point set may consist of type(1),type(3)and type(4)fixed points in Theorem 3.1,actually there are no type(1)fixed points by the assumption that the action is nontrivial and Theorem 3.2.

Leta3,a4be the numbers of groups of fixed points of type(3)and type(4),respectively.Then we have

Here we use the fact that def(3)=?8 and def(4)=?4.The solutions fora3,a4area3=4nanda4=0.Then the fixed point set consists of 4ngroups of type(3)fixed points in Theorem 3.1,and then the theorem follows.

Proof of Theorem 1.2Suppose that there exists such an action,and without loss of generality,we may assume the action is periodic with prime orderp.We complete the proof in two parts respectively:(i)When the action is pseudofree,and(ii)when the fixed point setFcontains 2-dimensional components.The tools we use areg-signature theorem and Lefschetz fixed point formula.

For part(i),by Theorem 3.2,we may assume that there are no fixed points with local representations contained inSL2(C).Then we exclude the cases whenp=2,since each type of fixed point datum is(k,?k).

Whenp=3,we assume all the fixed points with local representations of type(k,k).With the contribution

the signature ofXis sign(X)=?32 and|F|=χ(X)=48,a calculation of the weak version of theg-signature theorem

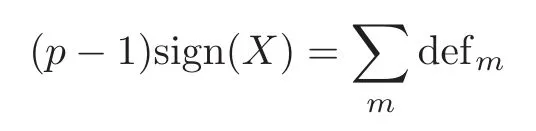
follows that?64=?32 which is a contradiction.

Whenp＞3,the fixed points of(k,?k)type are ruled out as well.From Section 3,we denoteδ2,δ3andδ4to be the numbers of Λαas a cusp-sphere component,a union of two(?2)-spheres,and a union of three spheres,respectively.The action is homologically trivial.Then|F|=χ(X),and a contradiction is reached by

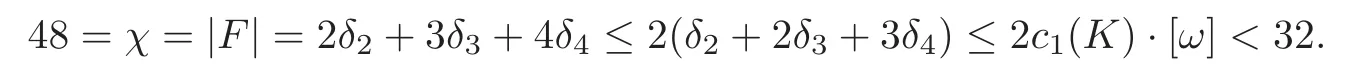
For part(ii),the fixed point setFcontains a 2-dimensional component,and theg-signature theorem is equivalent to the following equation:

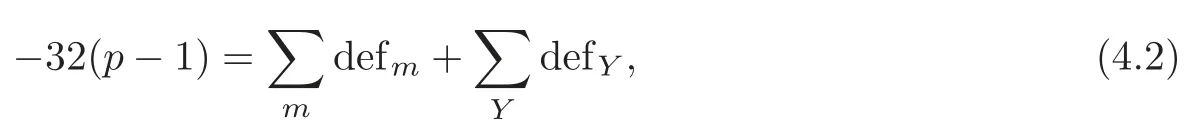
where defm=Ip,qdetermined by corresponding type,and defNote that a toroidal fixed component makes no contribution to the signature defect.We may only consider the cases that Λαcontains only embedded(?2)-spheres components when calculating the defects defYof theg-signature formula.

Ifp=2,then each point with local representation contained inSL2(C)makes no contributes,and everyYcontributes

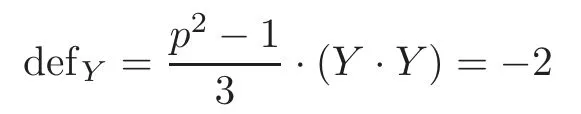
to theg-signature theorem.Then the equation(4.2)follows that?32=?2δY,where we denoteδYas the number of the fixed(?2)-spheresY.Thus we reach a contradiction since there exist at most 5 fixed(?2)-spheres under the restrictionc1(K)·[ω]＜16.

Ifp=3,then

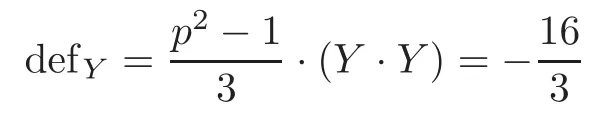
for eachY,and there are two types of fixed points with local representations(z1,z2)andcontributingrespectively.The restrictionc1(K)·[ω]＜16 follows that the number of fixed(?2)-spheres is at most 5.Note thatδm+2δY=χ(X)=48.We may reach a contradiction with a calculation to theg-signature theorem

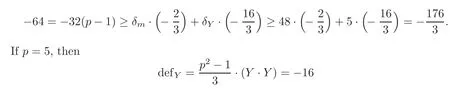
and

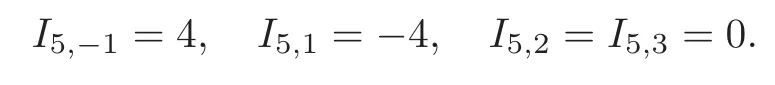
We denoteδΓαto be the number of Γαcomponents,where Γαstands for the corresponding type of components ascomponents.We also denoteδ4as the number ofcomponents that three spheres intersecting at a single point,δ3as the number of components with type(B),tas the number of the fixed tori,andδ1as the number of isolated fixed points with representations contained inSL2(C).Then the restriction and the Lefschetz fixed point theorem follow that

Some results may follow from the two formulae above that 0≤δY≤3,

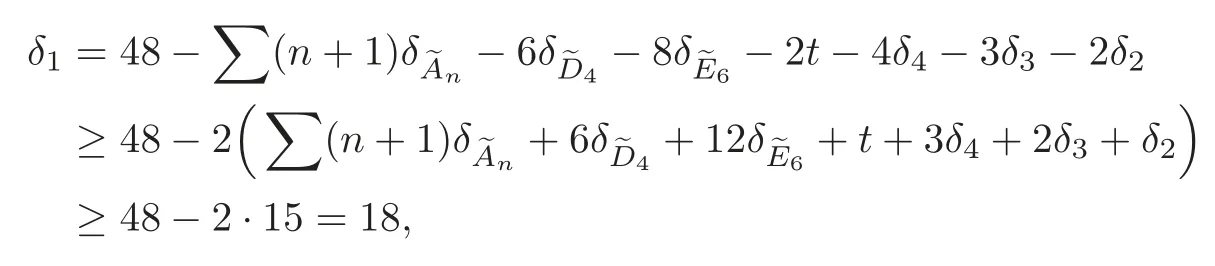
and the number of other isolated points insatisfying

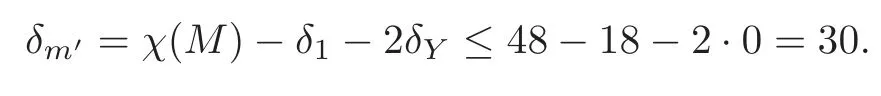
Note that defm′≥min{I5,q|q=1,2,3}=?4.We may easily obtain the inequality

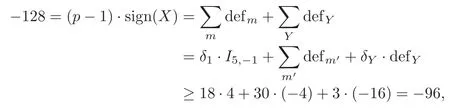
which is a contradiction.

Ifp≥7,there are no types more thanWe may introduce a mean contribution of each type to the defect ofg-signature theorem(see Section 5)to carry through the proof.If we setas the mean contribution for each type of Γα,then we claim that

for each type ofwith fixed 2-dimensional components(for explicit fixed point datum of certain types,one may see[17]).Note that

fork=2,3,4,where def(k)denotes the corresponding defect of the cusp sphere type,type(B)with two spheres intersecting at a point of order 2,and thetype with three spheres intersecting at a single point,respectively.The Lefschetz fixed point theorem and the restrictionc1(K)·ω＜16 follow that

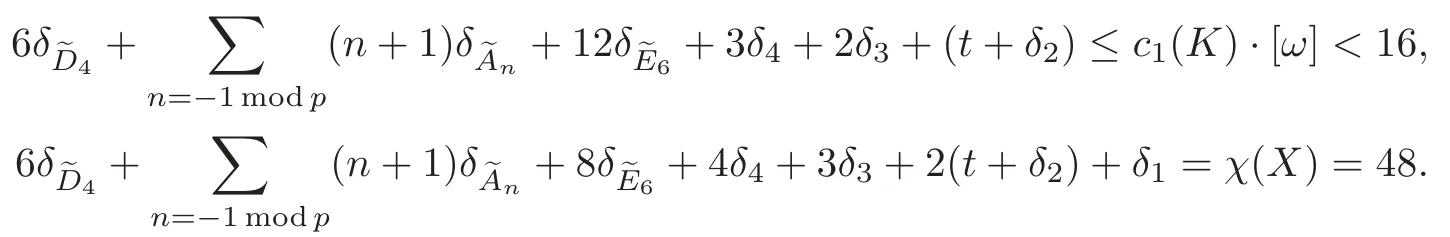
Similar results may follow the two formulae above thatδ1≥18,

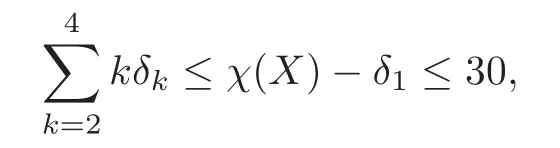
andweighttΓα·δΓα＜16 with Γαtaking over all the types ofSubstituting equations(4.3)–(4.4)into theg-signature theorem,we may reach a contradiction as follows obviously:

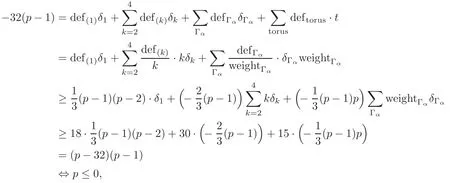
and complete the proof of Theorem 1.2.

For more details,we give the specifications of zooming the mean contribution to thegsignature theorem for each type in Section 5.

Remark 4.1In the pseudofree case in part(i),we may replace the restriction toc1(K)·[ω]＜24,and the rigidity property still remains.In fact,if the minimal symplectic manifold is(E(n),ω)with=0,≥2 andc1(K)·[ω]＜6n,we can maintain that there are no nontrivial homologically trivial pseudofree actions of a finite group onE(n)surface,which preserve the symplectic structureω.

Remark 4.2In fact,for the case thatp=5,we can also reach a contradiction to theg-signature theorem by resizing the mean contributions in Section 5.

5 Appendix

A calculation of signature defect we use in theg-signature theorem along this paper is expressed in this section.We follow the notations above that for an isolated fixed pointm∈F,the local representation atmisfor somek≠0 modpandq≠0 modp,then the signature defect defmof theg-signature theorem is given by

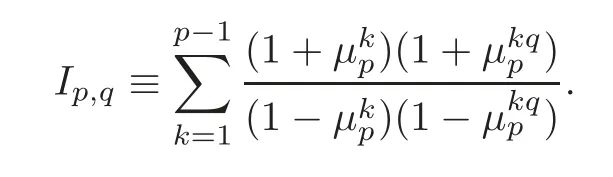
It is obvious thatIp,?q=?Ip,q.

Recall the relationship between the defect and the Dedekind sum(see[11])thatIp,q=?4p·s(q,p).Some results are collected from the direct computation of the equation

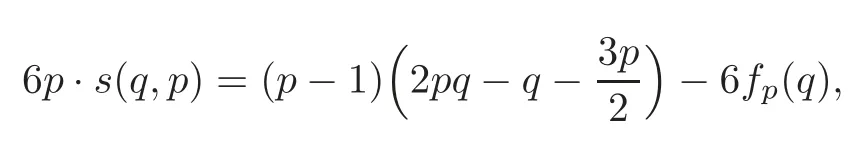
where(see[4]for more details):

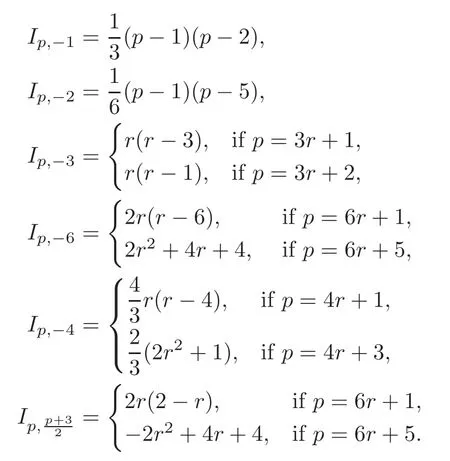
We take the results in a different statement and with the datum above directly evaluate the defects of type,type(B)and the cusp sphere type to theg-signature formula whenp≥5,that obviously summarize(4.4)as follows.

The typecomponent contributes

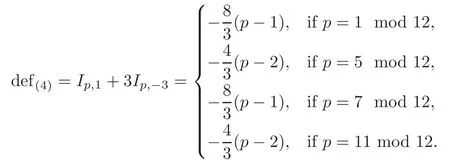
The type(B)component contributes

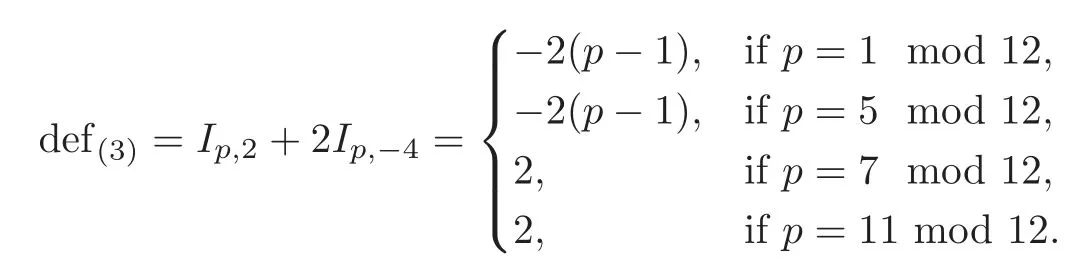
The cusp sphere component contributes

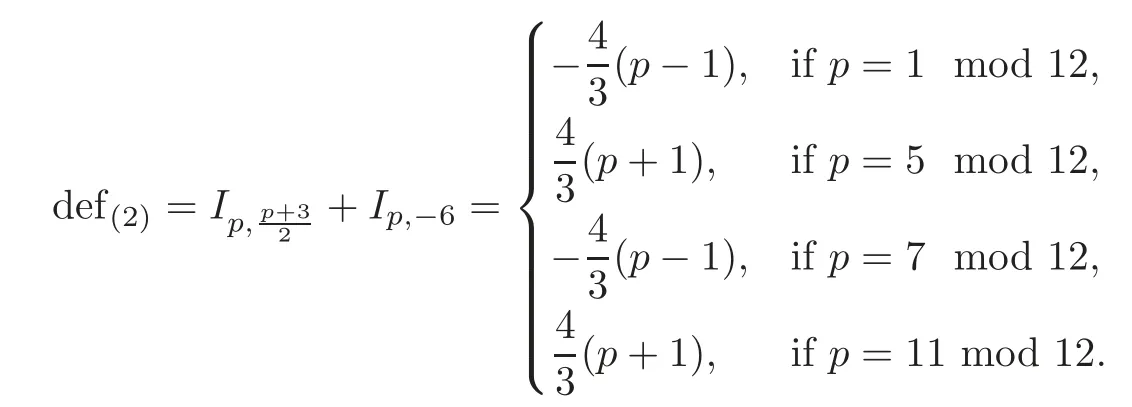
Based on the datum above,we formulate the defects of typeandforp≥5,which obviously support(4.3).

Atype contributes a(?2)-sphere and 4 fixed points with the same type(1,?2)toXG.With weight 6,the mean contribution

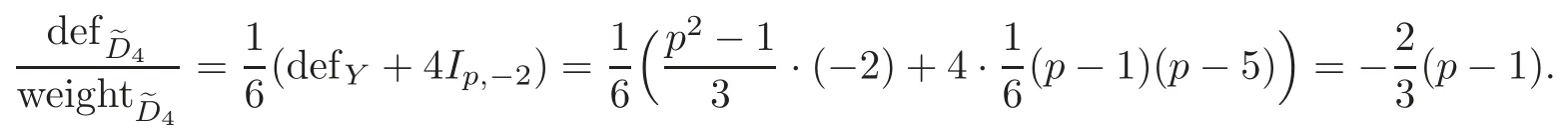
Antype contributes a(?2)-sphere and 6 fixed points toXG,so that the total defects

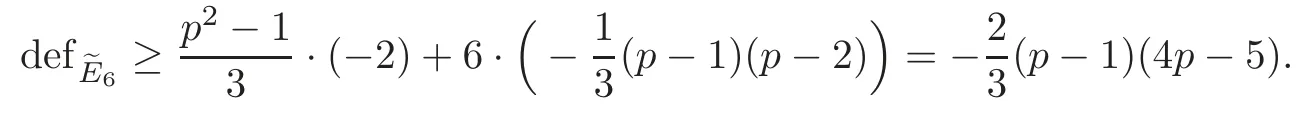
With weight 12,we have

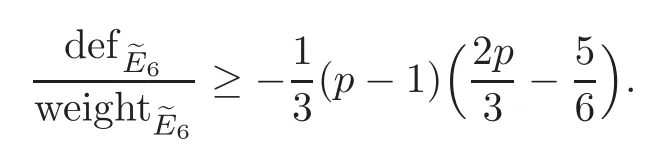
Antype,wheren=?1 modp,contributes a fixed(?2)-sphere andn?1 fixed points.Then

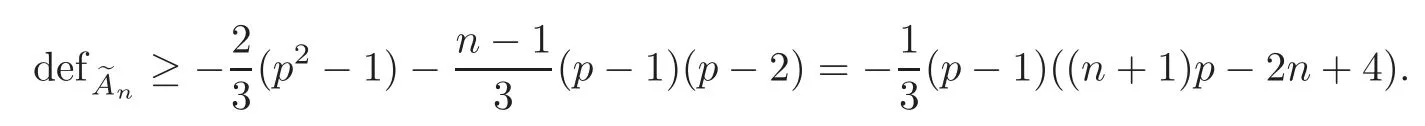
With weightn+1,we resize the mean contribution oftype as

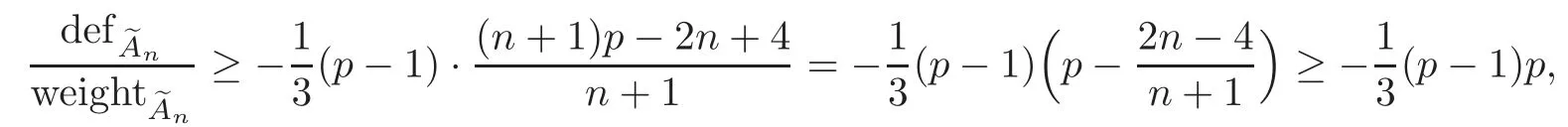
independent ofn.

[1]Atiyah,M.F.and Bott,R.,A Lefschetz fixed point formula for elliptic complexes:II.Application,Ann.of Math.,88,1968,451–491.

[2]Barth,W.,Peter,C.and Van de Ven,A.,Compact Complex Surfaces,Springer-Verlag,Berlin,Heidelberg,New York,Tokyo,1984.

[3]Chen,W.,Group actions on 4-manifolds:Some recent results and open questions,Proceedings of 13thG?kova Geometry-Topology Conference,2009,1–21.

[4]Chen,W.and Kwasik,S.,Symplectic symmetries of 4-manifolds,Topology,46(2),2007,103–128.

[5]Edmonds,A.L.,Construction of group actions on four-manifold,Trans.Amer.Math.Soc.,299,1987,155–170.

[6]Edmonds,A.L.,A survey of group actions on 4-manifolds,arXiv:0907.0454.

[7]Edmonds,A.L.and Ewing,J.H.,Realizing forms and fixed point data in dimension four,Amer.J.Math.,114,1992,1103–1126.

[8]Fintushel,R.and Stern,R.,Knots,links and 4-manifolds,Invent.Math.,134,1998,363–400.

[9]Gompf,R.E.and Stipsicz,A.I.,4-Manifolds and Kirby Calculus,Amer.Math.Soc.,Providence,RI,1999.

[10]Gordon,C.McA.,On theg-signature theorem in dimension four,A la Recherche de la Topologie Perdue,Progress in Math.,62,1986,159–180.

[11]Hirzebruch,F.and Zagier,D.,The Atiyah-Singer Theorem and Elementary Number Theory,Math.Lect.Series 3,Publish or Perish,Inc.,1974.

[12]Kwasik,S.and Schultz,R.,Homological properties of periodic homeomorphisms of 4-manifolds,Duke Math.J.,58,1989,241–250.

[13]Liu,X.and Nakamura,N.,PseudofreeZ3-actions onK3 surfaces,Proc.Amer.Math.Soc.,135(3),2007,903–910.

[14]Liu,X.and Nakamura,N.,Nonsmoothable group actions on elliptic surfaces,Topol.Appl.,155,2008,946–964.

[15]Matumoto,T.,Homologically trivial smooth involutions onK3 surfaces,Aspects of Low-dimensional Manifolds,Matsumoto,Y.and Morita,S.(eds.),Advanced Studies in Pure Mathematics,20,365–376,Kinokuniya,Tokyo,1992.

[16]McCooey,M.,Symmetry groups of four-manifolds,Topology,41(4),2002,835–851.

[17]Orlik,P.,Seifert manifolds,Lect.Notes in Math.,291,Springer-Verlag,Berlin,Heidelberg,New York,1972.

[18]Peters,C.A.M.,On automorphisms of compact K?hler surfaces,Algebraic Geometry,Angers,1979:249–267.

[19]Ruberman,D.,Involutions on spin 4-manifolds,Proc.Aemr.Math.Soc.,123(2),1995,593–596.

[20]Taubes,C.,The Seiberg-Witten invariants and symplectic forms,Math.Res.Lett.,1,1994,809–822.

[21]Taubes,C.,SW?Gr:From the Seiberg-Witten equations to pseudohollomorphic curves,J.Amer.Math.Soc.,9,1996,845–918.