劉玉萍

近幾年, 隨著數(shù)學(xué)教學(xué)中“問題解決”的提出,數(shù)學(xué)教學(xué)的改革在不斷深化,全國各地中?高考試卷逐漸滲透一些格調(diào)清新?別開生面的開放性試題,加大了知識(shí)間的聯(lián)系,突出綜合性,較好地發(fā)揮了選拔功能?這種試題目前被認(rèn)為最富有教育價(jià)值?最能開拓學(xué)生思維的問題?

數(shù)學(xué)開放性問題是相對(duì)傳統(tǒng)封閉題而言,或者條件不完全確定的?或者結(jié)論不唯一 ?甚至沒有標(biāo)準(zhǔn)答案的問題?

1.開放性問題的特點(diǎn):

1.1可接受性

開放性問題起點(diǎn)低?層次多?答案不唯一?解題策略多樣化?如:①邊長為12厘米的正方形可以分割為幾個(gè)邊長為整數(shù)的正方形?②給一個(gè)直角型的樓梯鋪上地毯,需要測(cè)量哪些數(shù)據(jù)?這些問題與生活較接近,學(xué)生較熟悉,容易主動(dòng)接受,易產(chǎn)生一種"試一試"的心理?他們的答案有些易找到,有的較難,每個(gè)學(xué)生都有參與解決問題的機(jī)會(huì),都愿意通過嘗試解決問題去獲得一些知識(shí)或者學(xué)習(xí)方法?這種可接受性,使開放性問題還能引發(fā)多層次學(xué)生的參與?如:用2根相等的長棒,2根相等的短棒,擺成一個(gè)四邊形,你能擺幾種圖形?對(duì)這類問題,基礎(chǔ)差的學(xué)生能得出簡(jiǎn)單的圖形,而基礎(chǔ)好的學(xué)生則能有序地考慮問題,盡量避免答案的重復(fù)與遺漏?而且答案的完整性,更能反映學(xué)生的思唯層次?舉舉手,能摘到果子;跳一跳,能摘到更多?更好的果子?恰當(dāng)?shù)剡\(yùn)用開放性問題,對(duì)培養(yǎng)學(xué)生的數(shù)學(xué)興趣,激發(fā)他們學(xué)習(xí)的動(dòng)機(jī),具有積極的作用?教師可恰當(dāng)?shù)夭贾靡恍╅_放性問題,給學(xué)生充分的思考時(shí)間與活動(dòng)空間去解決,讓他們充分享受收獲的喜悅?并在課堂上讓學(xué)生交流不同的解題方法,展示解題思路,從而發(fā)現(xiàn)學(xué)生的學(xué)習(xí)潛能,進(jìn)一步加以挖掘?培養(yǎng),讓學(xué)生的“果子”越摘越多,越摘越好,讓他們感受到,原來覺得枯燥無味的數(shù)學(xué),學(xué)起來竟是這樣的其樂無窮,越學(xué)越想學(xué),越學(xué)越愛學(xué),越學(xué)越會(huì)學(xué)?這樣,學(xué)生的主動(dòng)性便可充分地發(fā)揮出來?

1.2障礙性

開放性問題由于答案不唯一,題型新穎,題目涉及面較廣,沒有現(xiàn)成的解題模式可套用,其條件可能不完善,需要在解題過程中不斷完善,不斷假設(shè)條件,因此,學(xué)生不能一眼看出答案,學(xué)生必須從實(shí)際問題中抓住本質(zhì),提煉成數(shù)學(xué)問題,用數(shù)學(xué)思想去思考,用數(shù)學(xué)方法去解決?

如:某文具店出售每?jī)?cè)為122元和80元的兩種紀(jì)念冊(cè),兩種紀(jì)念品每?jī)?cè)都有30%的利潤,但每?jī)?cè)122元的不好出售,某人用1095元錢欲買一定數(shù)量的122元的紀(jì)念冊(cè)?店經(jīng)理雖然發(fā)現(xiàn)錢不夠,但認(rèn)為所獲得的利潤比出售同冊(cè)數(shù)的80元的紀(jì)念冊(cè)獲利還多,因此成交了這筆生意?請(qǐng)問:此人欲買多少冊(cè)122元紀(jì)念冊(cè)?

評(píng)析:這是一道關(guān)于商家如何靈活經(jīng)營,以獲取最大利潤的問題?首先,此人欲買幾冊(cè)?條件沒給出?再者,冊(cè)數(shù)是一整數(shù),這一隱含條件,學(xué)生不易想到,而隱含條件在解題過程中,何時(shí)用上,更是解題的難點(diǎn)?學(xué)生只有認(rèn)真分析題意,從實(shí)際問題中抓住本質(zhì):出售x冊(cè)122元的利潤比出售x冊(cè)80元的利潤還多,建立數(shù)學(xué)模型,由 1095-122×(1-30% )X > 80× 30% X (由于客人錢不夠,因此X >1095/122),再利用x的整數(shù)性質(zhì),解得x為9或?yàn)?0?

開放性問題條件的不完備或結(jié)論不唯一等特點(diǎn),雖然常給解題造成一定的障礙,但從另一方面,卻促使學(xué)生在解決問題的過程中,要通過觀察?猜測(cè)?檢驗(yàn)?修正?證明?推廣等各種數(shù)學(xué)方法去揭示問題的關(guān)鍵?這一過程不僅需要豐富的想象力?敏銳的思維能力,去及時(shí)發(fā)現(xiàn)可利用的條件,而且長時(shí)間的鉆研,需要足夠的耐心和細(xì)致,突破難點(diǎn)更需要足夠的意志和毅力?可見,開放性問題障礙性,有利于培養(yǎng)學(xué)生的學(xué)習(xí)能力,還有利于培養(yǎng)他們的學(xué)習(xí)品質(zhì),在促進(jìn)智力因素發(fā)展的同時(shí),也促進(jìn)非智力因素的發(fā)展?

1.3探索性

開放性問題的結(jié)論常是豐富多彩的,非單調(diào)的,而解題模式?解題途徑的多樣性,決定了必須從全方位,多角度去觀察?分析,充分揭示問題的本質(zhì)特征,達(dá)到解決問題的目的?如:一個(gè)因數(shù)是18,另一個(gè)因數(shù)2分別擴(kuò)大5倍?10倍?100倍,積怎樣變化?再如:有一棱長為2厘米的正方體,將它沿某些棱剪開,有幾種展開圖?這個(gè)問題的條件并沒有規(guī)定用何種方式剪,思維的策略不同決定裁剪的方式不同,引發(fā)多種解題方法與結(jié)論?再如:兩個(gè)人輪流報(bào)數(shù)(自然數(shù)),報(bào)出的數(shù)不能超過8,把兩人報(bào)的數(shù)加起來,誰報(bào)數(shù)后加起來的數(shù)是88(或88以上的數(shù)),誰就獲勝?如果讓你先報(bào)數(shù),第一次報(bào)多少就一定獲勝?這個(gè)問題則應(yīng)該通過不斷的探索?找規(guī)律,從而得出這個(gè)數(shù)為7?

開放性問題的探索性,有利于促進(jìn)學(xué)生的創(chuàng)造性思維的發(fā)展?首先,開放性問題情景的創(chuàng)設(shè),使學(xué)生置身于知識(shí)發(fā)展過程中,發(fā)現(xiàn)差異,提出疑問,主動(dòng)帶著懷疑的眼光去發(fā)現(xiàn)問題,造成知識(shí)沖突,教師啟發(fā)誘導(dǎo),讓學(xué)生進(jìn)入更深一層的思維;其次,及時(shí)展示思維過程,讓學(xué)生觀察?類比?總結(jié),從中找出異同點(diǎn);同時(shí),組織適當(dāng)?shù)膯栴}鏈,利用問題鏈所具有的聯(lián)系性和發(fā)散性,引發(fā)學(xué)生通過對(duì)問題追根刨底的探索,達(dá)到創(chuàng)造性思維開發(fā)的目的?如:講授定理:三角形內(nèi)角和等于180°時(shí),教師啟發(fā)學(xué)生思考:三角形的外角和等于多少?進(jìn)一步問:四邊形的外角和呢?n邊形的內(nèi)角和與外角和又為多少?有何規(guī)律?讓學(xué)有余力的學(xué)生去摸索?再如:一個(gè)街區(qū)有3條橫街?3條縱街,如圖①一個(gè)人從左上角A處出發(fā)依最短途徑走到右下角B處,共有多少種不同的走法?若街區(qū)有5條橫街,5條縱街,如圖②又將有幾種走法呢?

評(píng)析:通過觀察,在多數(shù)街道的交叉口,按照最短途徑的要求,行人都只有兩種選擇:向右橫走或向下走縱街,圖(1)較為容易求得6種情況,可圖(2)具體計(jì)算則不勝其繁,但只要類比圖(1),找出規(guī)律:行人從A——B均由4段橫街和4段縱街構(gòu)成,因此,每一種走法都對(duì)應(yīng)一種這4橫4縱的有序排列,反之亦然,因此,所求的不同最短途徑數(shù)就等于 8!/4!4!=70種?

2.開放性問題的類型:

2.1條件開放型

即問題的條件不完備或滿足結(jié)論的條件不唯一?如:姐姐買蘋果花了50元錢,售貨員找給8元錢,你知道姐姐買了幾斤蘋果嗎?題中沒給出蘋果的單價(jià),因此答案不唯一?又如:某校向希望工程捐款活動(dòng)中,甲班的m個(gè)男生和11個(gè)女生的捐款總數(shù)與乙班的9個(gè)男生和n個(gè)女生的捐款總數(shù)相等,都是(mn+9m+11n+145),已知每人的捐款數(shù)相同,且都是整數(shù)元,求每人的捐款數(shù)及m?n的值(96年全國初中聯(lián)賽試題)?此題可設(shè)每人捐款數(shù)為x元,據(jù)每人的捐款數(shù)及每班的捐款數(shù)均為不變量,列不定方程組:mx+11x = 9x+nx = mn+9m+11n+145再利用整數(shù)的性質(zhì)得(1)m=35,n=37,x=47;(2)m=12,n=14,x=25?此題雖然條件不完備,解之有困難,但它提供給興趣愛好者一個(gè)廣闊的思維空間,使每一位解題的人都以自己的數(shù)學(xué)背景和理解角度出發(fā),獲得對(duì)問題的解答.

2.2結(jié)論開放型

即在給定條件下,結(jié)論不唯一或不確定?

如:(統(tǒng)計(jì)開放型)

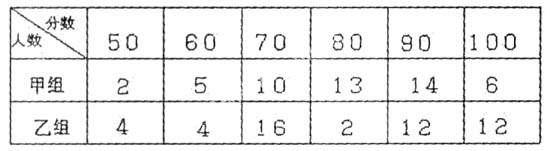
一次科技知識(shí)競(jìng)賽中,兩組學(xué)生成績(jī)統(tǒng)計(jì)如下:

已經(jīng)計(jì)算兩組的人均分都是80分,請(qǐng)你根據(jù)所學(xué)過的統(tǒng)計(jì)知識(shí),進(jìn)一步判斷這兩組競(jìng)賽中成績(jī)誰優(yōu)誰次,并說明理由?

評(píng)析:這道題新穎別致,結(jié)論具有開放性,正確答案必須抓住“根據(jù)所學(xué)過的統(tǒng)計(jì)知識(shí)”,從眾數(shù)?中位數(shù)?方差?高分等幾個(gè)角度去進(jìn)行必要的計(jì)算?評(píng)估,從而判斷說明成績(jī)誰優(yōu)誰次?①從眾數(shù)看,甲90分,乙70分,甲組成績(jī)較好;②從方差看,可求得S²甲 =172 ,S²乙=256 , S²甲2