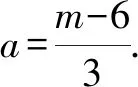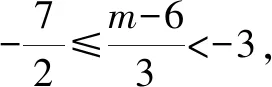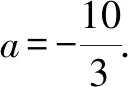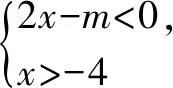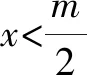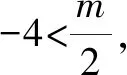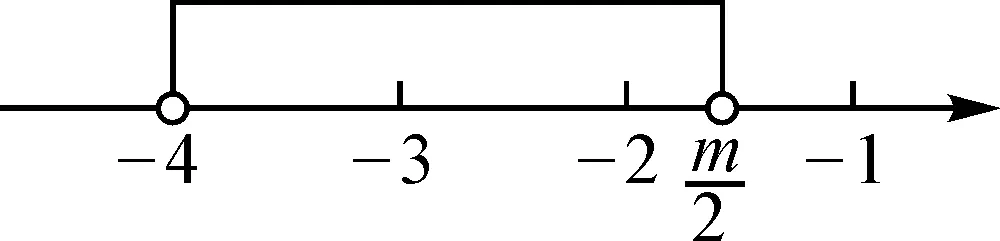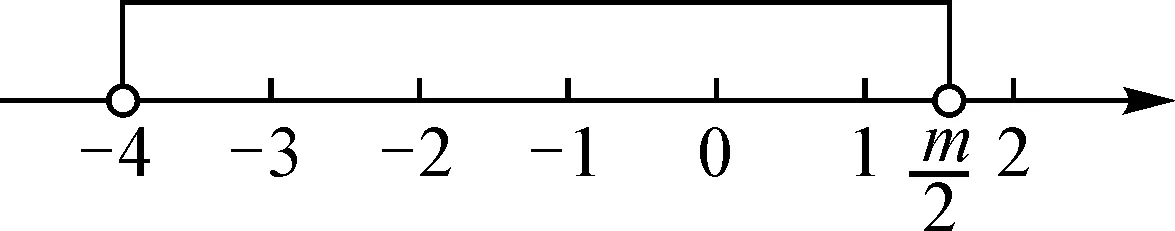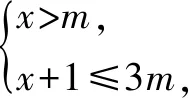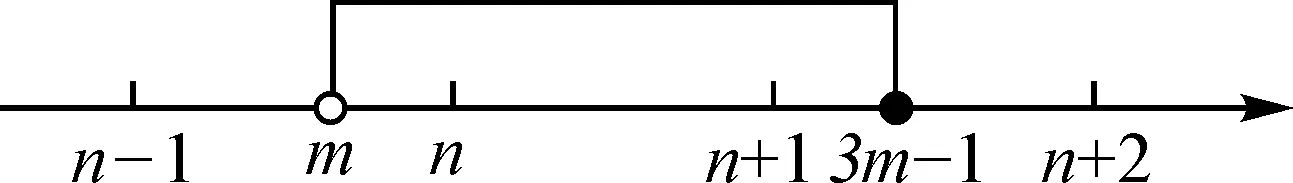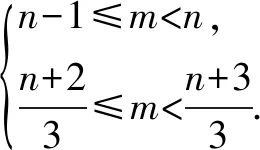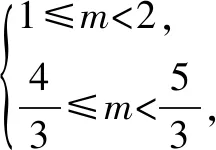巧解含參不等式(組)整數(shù)解問題
邱 雯
? 廣東省惠州市第八中學
對于只有一個不等式含參數(shù)的不等式組,求參數(shù)值(或范圍)問題是中考的一個重要考點,大多數(shù)學生通過多次訓練或許能夠掌握.而對于不等式組中每個不等式都含有參數(shù)的問題,命題涉及較少.這類問題又該如何解答呢?下面結合例題進行剖析.
1 整數(shù)解個數(shù)(或數(shù)值)明確
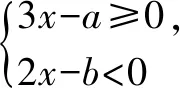
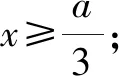
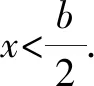
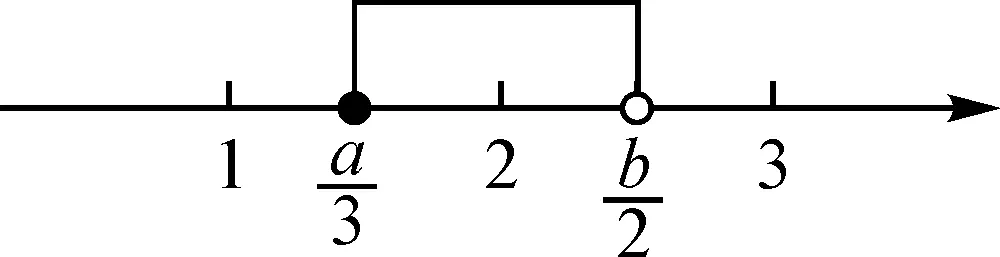
圖1
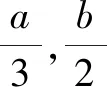
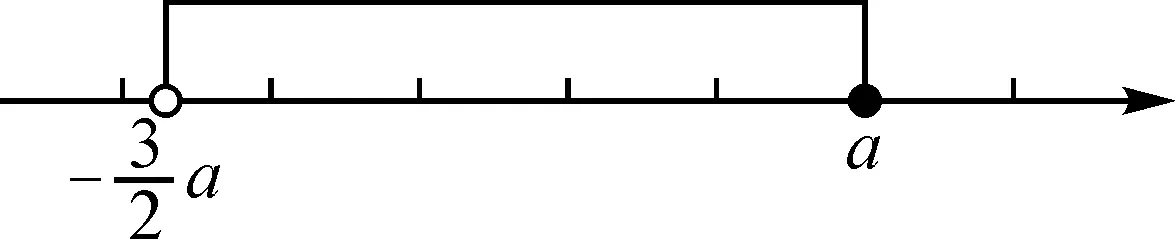
解得3 又a,b均為整數(shù),當a=6,b=6時,2a2+b取得最大值為2×62+6=78. 點評:此題用用含a,b的式子表示不等式組的解集;再根據(jù)解集中“整數(shù)解僅為2”,建立與a,b有關的新的不等式組,從而確定參數(shù)a,b的范圍(或取值). 圖2 解得0≤a<6,15 所以15 圖3 所以整數(shù)a的最小值是2. 點評:根據(jù)條件“解集中至少有5個整數(shù)解”,建立與a有關的不等式是解題的關鍵所在,通過數(shù)軸將“數(shù)”轉化為“形”,再將“形”轉化為“數(shù)”. 例4(2021江漢)已知關于x的不等式x-a<0的最大整數(shù)解為3a+6,則a的值為______. 解:由x-a<0,得x 又不等式的解集中最大整數(shù)解為3a+6,則與a最接近的兩整數(shù)為3a+6與3a+7. 將解集及表示數(shù)3a+b與3a+7的點在數(shù)軸上表示出來,如圖4所示. 圖4 點評:用含a的式子表示解集范圍,再根據(jù)“3a+6為最大整數(shù)解”,建立與a有關的不等式組,求得a的取值范圍,再通過增設變量表示3a+6的值,進而求得a的值. 因為不等式組的整數(shù)解之和是-5,所以不等式組的解整數(shù)解為-3,-2或-3,-2,-1,0,1. 當不等式組的整數(shù)解為-3,-2時,解集在數(shù)軸上的表示如圖5所示. 圖5 當不等式組的整數(shù)解為-3,-2,-1,0,1時,解集在數(shù)軸上的表示如圖6所示. 圖6 綜上,m的取值范圍是-4 點評:由已知條件“所有整數(shù)解的和為-5”得出兩組不同的整數(shù)解,再分類討論建立與m有關的不等式組,問題迎刃而解. 又不等式組有解,則m 設四個相鄰的整數(shù)分別為n-1,n,n+1,n+2. 令不等式組的兩個整數(shù)解為n和n+1,將不等式的解集在數(shù)軸上表示出來,如圖7所示. 圖7 所以n-1≤m 又因為n為整數(shù),所以n=2. 點評:首先解原不等式組得x的解集,再根據(jù)“x僅有2個整數(shù)解”建立關于整數(shù)n的不等式組,并求出整數(shù)n,進而求出m的范圍. 解決含參不等式組的整數(shù)解問題,一般先把參數(shù)看成已知數(shù)求出不等式組的解集,再借助整數(shù)解的條件確定整數(shù)解的個數(shù)(或具體數(shù)值),將解集在數(shù)軸表示出來,關注解集的上下限所表示的點在數(shù)軸上的位置,建立與參數(shù)有關的不等式(組),解新的不等式組即求出所要的結果.Z
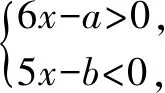
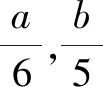

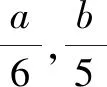
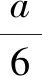
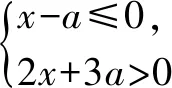
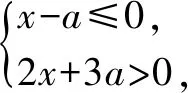
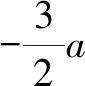
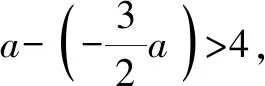
2 整數(shù)解的值不明確