徐 樂(lè)

? 江蘇省靖江市外國(guó)語(yǔ)龍馨園學(xué)校

圓是初中數(shù)學(xué)平面幾何中非常重要的一個(gè)知識(shí)點(diǎn),與初中數(shù)學(xué)中其他幾何問(wèn)題有著緊密的聯(lián)系.所以在解決幾何問(wèn)題時(shí),一些無(wú)法利用常規(guī)思路求解的綜合問(wèn)題可以嘗試通過(guò)構(gòu)造輔助圓的方式來(lái)解決.因此,在初中數(shù)學(xué)幾何問(wèn)題解題教學(xué)中,教會(huì)學(xué)生如何正確使用輔助圓來(lái)巧解幾何問(wèn)題是教師需要重點(diǎn)研究的問(wèn)題.下面將通過(guò)例題對(duì)輔助圓的應(yīng)用進(jìn)行說(shuō)明.

1 角的問(wèn)題

例1在△ABC中,AB=AC,∠ABC的平分線交AC于點(diǎn)D,已知BC=BD+AD,求∠A的度數(shù).

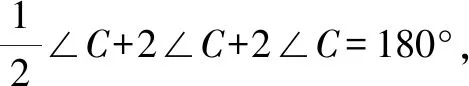
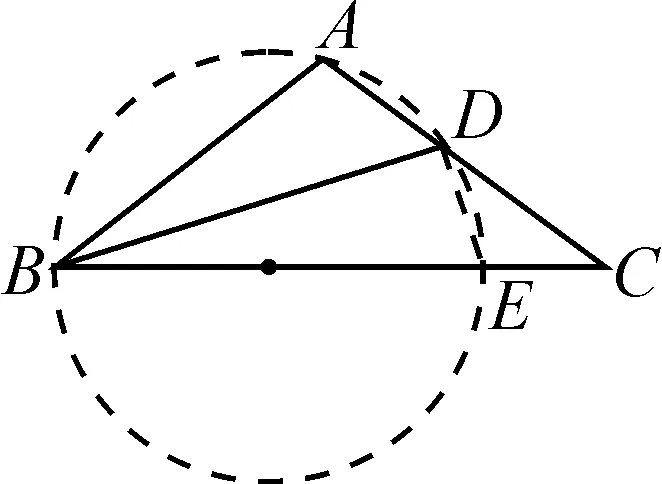
圖1

在初中數(shù)學(xué)幾何問(wèn)題中構(gòu)造輔助線需要充分結(jié)合試題的情況來(lái)進(jìn)行.本題中輔助圓的構(gòu)造就是結(jié)合了本題所給定的角平分線的關(guān)系,根據(jù)相等的圓周角所對(duì)應(yīng)的弧和弦長(zhǎng)相等的性質(zhì)來(lái)實(shí)現(xiàn);然后通過(guò)輔助圓及相關(guān)線段關(guān)系來(lái)與相關(guān)角取得聯(lián)系;最后利用三角形的性質(zhì)求解.教師要對(duì)學(xué)生進(jìn)行相應(yīng)的引導(dǎo),讓學(xué)生掌握通過(guò)角的關(guān)系來(lái)構(gòu)造輔助圓,進(jìn)而借助輔助圓解決問(wèn)題.

2 線段長(zhǎng)度的問(wèn)題

例2如圖2所示,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是Rt△ABC內(nèi)部的一個(gè)動(dòng)點(diǎn),且滿足∠PAB=∠PBC,則線段CP的最小值為( ).

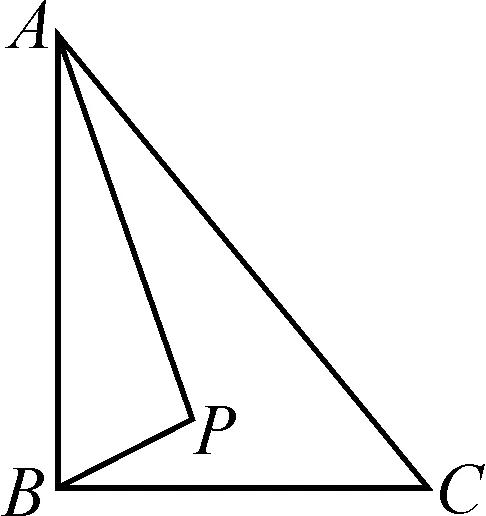
圖2

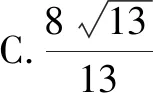
分析：根據(jù)AB⊥BC可以知道∠ABC=90°,結(jié)合∠PAB=∠PBC可得到∠APB=90°,所以△ABP是直角三角形.根據(jù)直角三角形中斜邊的中線等于斜邊的一半以及圓的直徑所對(duì)的圓周角是90°,可知點(diǎn)P在以AB為直徑的圓上.以AB的中點(diǎn)O為圓心,AB為直徑作圓,如圖3所示.這樣就可得到當(dāng)PC的值最小時(shí),點(diǎn)P正好在線段OC上.因?yàn)锳B=6,所以O(shè)B=3.在Rt△OBC中,BC=4,根據(jù)勾股定理得到OC=5,于是可求出PC的最小值為2.所以正確答案是選項(xiàng)B.

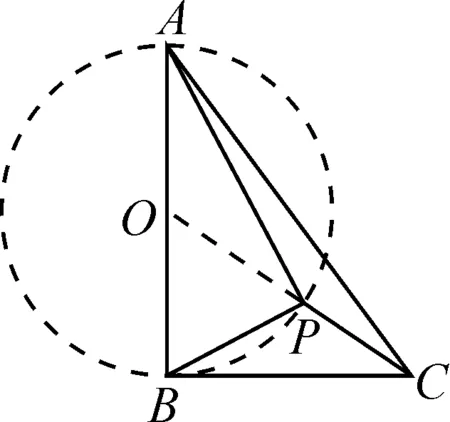
圖3

例2的解題關(guān)鍵是需要判斷點(diǎn)P的軌跡,首先根據(jù)試題中所給定的關(guān)系得到∠APB=90°,結(jié)合直角三角形的性質(zhì)和圓的性質(zhì)很容易判斷出點(diǎn)P在以直線AB為直徑的圓上,然后就能夠求解最小值.因此,在解題的過(guò)程中,只有認(rèn)真分析題目條件,才能順利找到解題思路.教師在進(jìn)行解題教學(xué)時(shí)需要教會(huì)學(xué)生如何根據(jù)題目中所給定的已知條件來(lái)進(jìn)行分析,從而找到解題思路.很多幾何問(wèn)題都是需要在解題的過(guò)程中才能夠找到相應(yīng)的解題思路,并不是通過(guò)對(duì)試題的觀察就能得到解題思路的.因此結(jié)合已知條件來(lái)對(duì)試題中存在的關(guān)系進(jìn)行分析,在解題的過(guò)程中發(fā)現(xiàn)解題思路,是解決問(wèn)題最好的方式.教師需要引導(dǎo)學(xué)生先根據(jù)已知條件嘗試找到解題的思路,進(jìn)而解決問(wèn)題.

3 三角形相似的問(wèn)題

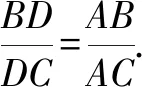
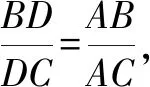
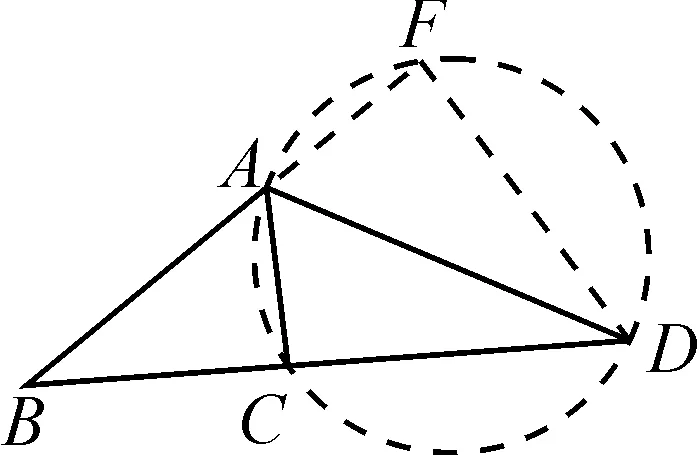
圖4

幾何問(wèn)題中需要求證的結(jié)論存在線段比例關(guān)系或者線段等積關(guān)系時(shí),都會(huì)涉及三角形相似或者全等的證明,通過(guò)構(gòu)造圓為三角形相似或者全等提供條件,實(shí)現(xiàn)對(duì)問(wèn)題的求解.在這個(gè)過(guò)程中,需要充分結(jié)合例題1和例題2中輔助圓構(gòu)造的方式來(lái)找到相應(yīng)的關(guān)系.

4 動(dòng)點(diǎn)的問(wèn)題

例4如圖5所示,邊長(zhǎng)為3的等邊三角形ABC,D,E分別是BC,AC邊上的兩個(gè)動(dòng)點(diǎn),且BD=CE,AD,BE交于點(diǎn)P,求點(diǎn)P的運(yùn)動(dòng)路徑長(zhǎng)和CP的最小值.

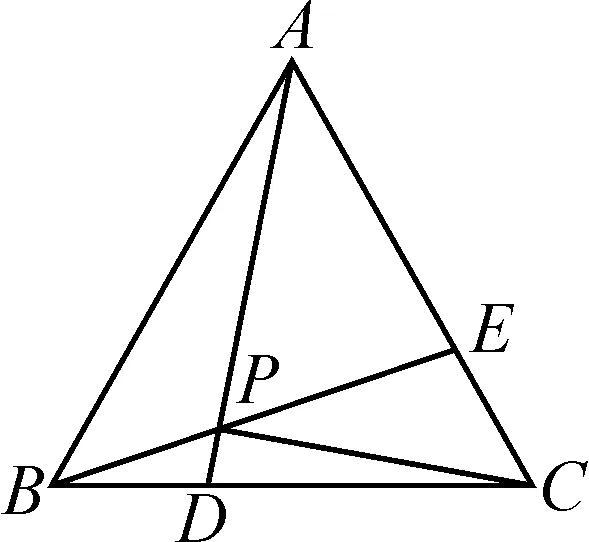
圖5

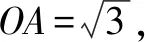
解：由AB=BC,∠ABD=∠BCE,BD=CE得△ABD≌△BCE.

由∠CBE+∠ABP=60°,得∠BAP+∠ABP=∠APE=60°.

所以∠APB=120°.

故點(diǎn)P的運(yùn)動(dòng)軌跡是以AB為弦的圓上的一段弧.

如圖6所示,作△ABP的外接圓,圓心為O,連接OA,OB,OP,OC.

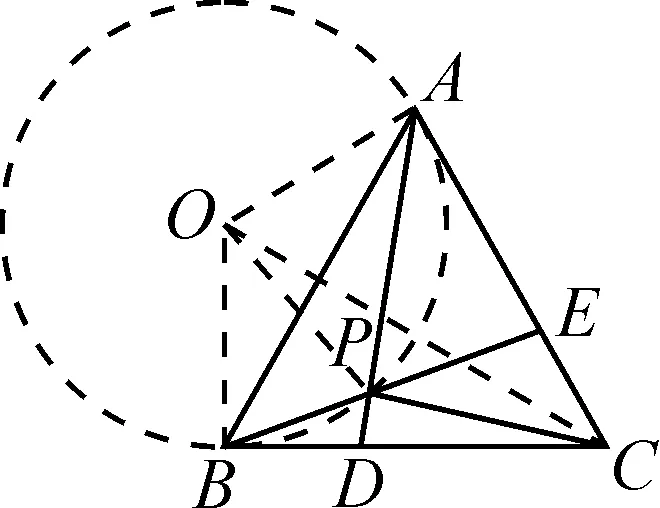
圖6

由OA=OB,AC=BC,得△AOC≌△BOC.

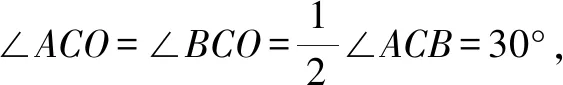
故∠OAC=90°.

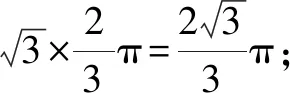
在三角形的動(dòng)點(diǎn)問(wèn)題中,如果動(dòng)點(diǎn)與一條線段所構(gòu)成的角度固定,則說(shuō)明這個(gè)動(dòng)點(diǎn)的軌跡是以這個(gè)線段為弦的圓上的一段弧,通過(guò)這個(gè)關(guān)系可以構(gòu)造輔助圓,然后利用圓的性質(zhì)來(lái)求解問(wèn)題.本題給定的是正三角形,當(dāng)然不同的三角形中所呈現(xiàn)的關(guān)系可能會(huì)存在差別,但是本質(zhì)沒(méi)有變化.例如,在例題2中通過(guò)計(jì)算所得到的角度為90°的特殊角,這個(gè)輔助圓的圓心就在直角三角形的斜邊上.例4中這個(gè)角度為120°,圓心在三角形的外部,通過(guò)輔助圓來(lái)充分利用圓的相關(guān)性質(zhì),能夠更好地對(duì)問(wèn)題進(jìn)行求解,實(shí)現(xiàn)問(wèn)題的解決.

本文中對(duì)輔助圓在初中數(shù)學(xué)平面幾何中的應(yīng)用進(jìn)行了總結(jié),并通過(guò)相關(guān)例題對(duì)其用法進(jìn)行了說(shuō)明.在初中數(shù)學(xué)平面幾何問(wèn)題中巧用輔助圓能夠優(yōu)化試題解法,實(shí)現(xiàn)快速求解.因此,教師在解題教學(xué)的過(guò)程中需要對(duì)學(xué)生進(jìn)行有效地引導(dǎo),讓學(xué)生掌握輔助圓的應(yīng)用,從而提升解題能力;提升數(shù)學(xué)素養(yǎng).Z