巨小鵬 黃龍海

(陜西省漢中市龍崗學校)

解題的目的在于化繁為簡,以此理解數(shù)學的本質(zhì).作者曾對同構(gòu)法在函數(shù)和解析幾何中的應(yīng)用做了歸納分析后,數(shù)列中的同構(gòu)思想解題也在課本中找到了其題根題源,特別是對一階遞推數(shù)列和二階遞推數(shù)列問題做以分析,尋找其規(guī)律,揭示其本質(zhì).

1.平凡見奇生面開——真題呈現(xiàn)

【例1】(2020·全國Ⅲ卷理·17)設(shè)數(shù)列{an}滿足a1=3,an+1=3an-4n.計算a2,a3,猜想{an}的通項公式并加以證明.

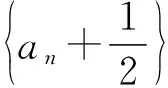
2.源頭活水清如許——課本尋根

陳景潤先生曾談起數(shù)學解題時說:“題有千變,貴在有根”.以題根為源展開探究,旨在找到破題方向,抓住解題思維入口,通過變式拓展理解解題“大道至簡”的解題模式,理解數(shù)學概念和定理(公式)的本質(zhì),找到題根題源,就找到問題的底層邏輯,以此展開思維繼續(xù)探究.

題源1(蘇教版(新版)高中數(shù)學選擇性必修一P163問題探究)若數(shù)列{an}滿足:a1=1,a2=5,對任意的n∈N*,都有an+2=4an+1-4an,求an的表達式.

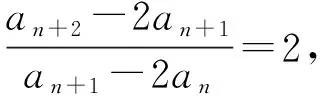
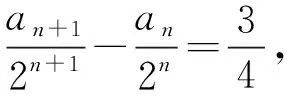
請仿照上面的解法,思考:已知數(shù)列{an}滿足:a1=1,a2=1,對任意的n∈N*,都有an+2=an+1-an,求an的表達式.(解析略)

題源2(蘇教版(新版)高中數(shù)學選擇性必修一P168第16題探究題)已知數(shù)列{an}滿足:a1=1,對任意的n∈N*,都有an+1=2an+1,求an的通項公式.

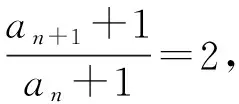
3.鴛鴦繡出教君看——同構(gòu)法問題解答

【例1解析】解法一:由題意可得a2=3a1-4=9-4=5,a3=3a2-8=15-8=7.猜想an=2n+1,證明:由a1=3,a2=5得a2-a1=2.因為an+1=3an-4n,an=3an-1-4(n-1)(n≥2),兩式相減得an+1-an=3(an-an-1)-4,令bn=an+1-an,且b1=2,所以bn=3bn-1-4,兩邊同時減去2,得bn-2=3(bn-1-2),且b1-2=0,所以bn-2=0,即an+1-an=2.又a2-a1=2,所以數(shù)列{an}是首項為3,公差為2的等差數(shù)列,所以an=2n+1.

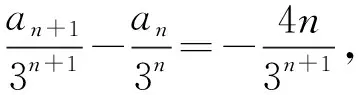
解法三:由題意可得a2=3a1-4=5,a3=3a2-8=7,猜想an=2n+1.證明:由于an+1=3an-4n,所以可設(shè)an+1+λ(n+1)+μ=3(an+λn+μ),其中λ,μ為常數(shù),整理得an+1=3an+2λn+2μ-λ,故2λ=-4,2μ-λ=0,解得λ=-2,μ=-1,所以an+1-2(n+1)-1=3(an-2n-1)=…=3n(a1-2×1-1).又a1-3=0,所以{an-2n-1}是各項均為0的常數(shù)列,故an-2n-1=0,即an=2n+1.

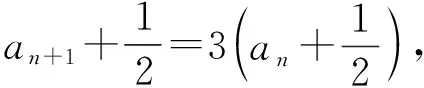
從兩個高考例題和題根中可以看出,解題過程中通過引導和同化,以順應(yīng)學生的思維層次和知識結(jié)構(gòu),讓學生從觀察到變形,將條件進行等價轉(zhuǎn)化,化成結(jié)構(gòu)形式相同的方程,然后構(gòu)造出等差(比)數(shù)列,從而利用熟悉的等差(比)數(shù)列定義或者性質(zhì)解決問題,起到化繁為簡的目的,我們將這種方法稱為“同構(gòu)法”.

4.悉數(shù)金針度與人——數(shù)列中應(yīng)用舉例揭規(guī)律

4.1方程中數(shù)列同構(gòu)問題

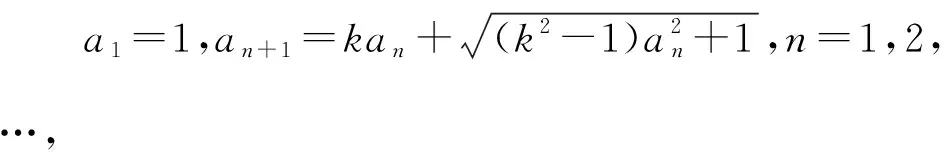
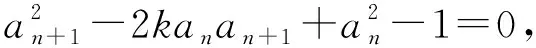
4.2遞推數(shù)列中同構(gòu)問題

類型一an+1=pan+q型

an+1=pan+q構(gòu)造同構(gòu)式an+1+m=p(an+m).例如題源2.

類型二an+1=pan+an+q型

an+1=pan+an+q構(gòu)造同構(gòu)式an+1+A(n+1)+B=p(an+An+B).

【例4】已知數(shù)列{an}中,a1=3,且滿足an+1=an+2n+2,bn=an-n2(n∈N*).證明:數(shù)列{bn}是等差數(shù)列,并求{bn}的通項公式.

【解析】證明:因為an+1=an+2n+2,所以an+1-(n+1)2=an-n2+1,故bn+1-bn=1,所以數(shù)列{bn}是等差數(shù)列,且公差為1.又b1=a1-1=2,故bn=2+(n-1)=n+1.

類型三an+1=pan+rpn+1型

an+1=pan+rpn+1型方法參考題源1.

類型四an+1=pan+rqn+1型

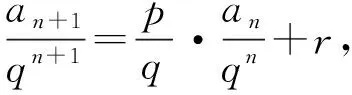
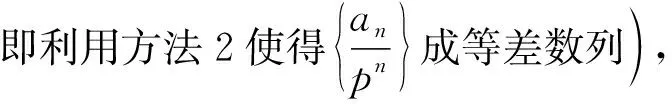
類型五an+1=manr型

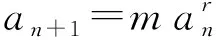
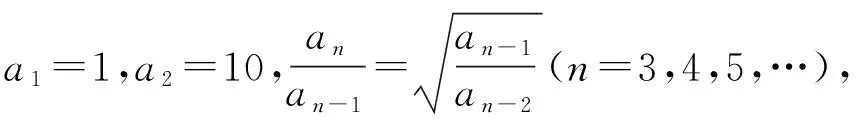
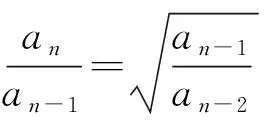
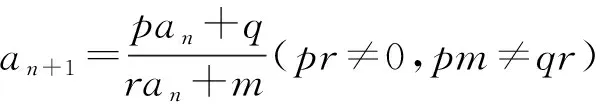
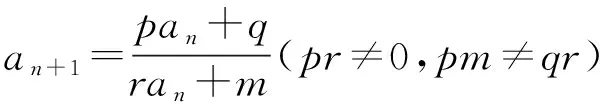
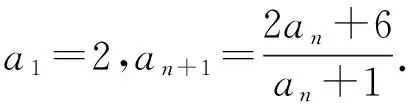
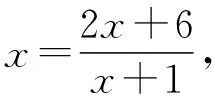
類型七an+2=pan+1+qan型

an+2=pan+1+qan構(gòu)造同構(gòu)式an+2-san+1=t(an+1-san),或者求出特征方程x2-px-q=0,特征根是α,β,若α≠β,則an=Aαn+Bβn,若α=β,則an=(An+B)αn,其中A,B為常數(shù),根據(jù)a1,a2的值,建立方程組求出常數(shù)A,B,即得an.

【例7】已知數(shù)列{an}滿足a1=2,a2=8,an+2=4an+1-3an.求{an}的通項公式.

【解析】解法一:方法如題源1得數(shù)列通項an=3n-1.

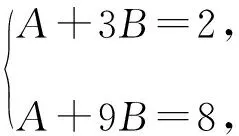
類型八an+2=pan+1+qan+t型

an+2=pan+1+qan+t構(gòu)造等差數(shù)列即可.

【例8】數(shù)列{an}滿足a1=1,a2=2,an+2=2an+1-an+2.設(shè)bn=an+1-an,證明{bn}是等差數(shù)列.

【解析】證明:由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即bn+1=bn+2.

又b1=1,所以數(shù)列{bn}是首項為1,公差為2的等差數(shù)列.

【評注】以上類型通過化歸與轉(zhuǎn)化為已知熟悉的形式解決問題,除了同構(gòu)轉(zhuǎn)化還利用了不動點法和特征根法解決問題,它們也具有同構(gòu)思想.