Dynamicsin a Non-Autonomous Predator-Prey System with Crowley-Martin Functional Response*
Azhar Halik,Ahmadjan Muhammadhaji
(School of Mathematicsand System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: A class of non-autonomous predator-prey system with Crowley-Martin functional response is discussed.Some sufficient conditions on the boundedness,permanence,extinction,existence of periodic solution and global attractivity of the system are established by using the comparison method and Lyapunov function method.
Key words:non-autonomous predator-prey system;crowley-martin functional response;permanence;global attractivity
0 Introduction
In thereal world,therearemany typesof interactionsbetween two species.Predator-prey relationsareamong themost common and primitive ecological interactions.It is worth noting that the whole field of mathematical ecology began with the studiesof population dynamicssubject to the predator-prey interaction,for example,the classical works by Lotka[1]and Volterra[2].Recently,many scholars at home and abroad have studied the population dynamical predator-prey systems[1-8]and many good results have been obtained.So far,most of the studies on the population dynamical predator-prey systems describethepredatorsand their prey dynamical interactionsusing thefunctional responsefunction(ratio dependent function)to describethepredator’spredation rateand conversion rate[3-8].For example,in[5]theauthorsconsidered thefollowing two species autonomous predator-prey system with Crowley-Martin functional response
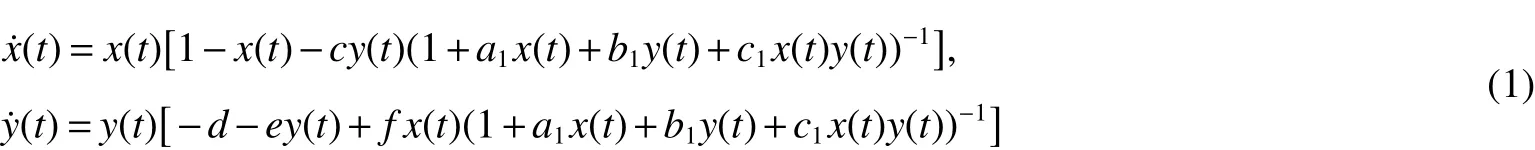
and obtained some sufficient conditions for the permanence,non-permanence,Local and global asymptotic stability of positiveequilibrium of model(1).Where x(t)and y(t)arerepresent the population density of prey species X and predator species Y.cy(t)(1+a1x(t)+b1y(t)+c1x(t)y(t))-1and fx(t)(1+a1x(t)+b1y(t)+c1x(t)y(t))-1arethe Crowley-Martin functional response.In[1]theauthorsuse Crowley-Martin functional responseto describethepredator-prey relations.
It is worth noting that the main difference between the Crowley-Martin functional response and Beddington-DeAngelis functional response is the Crowley-Martin functional response is predator dependent.Research[5]has shown that the predator-dependent functional responses can provide better description of predator feeding over a range of predator-prey abundance.
On the other hand,in nature,the habitat environment of the population will change along with the passage of time,and thisleadsto changesin thegrowth characteristicsof thesepopulations.Thus,weshould introduce non-autonomouscaseinto model foundation,will have more resemblance to the real ecosystem.Therefore,it is valuable and important to study the non-autonomouspopulation predator-prey dynamicsmodel.
Based on theaboveanalysisand reasons,in thispaper,weconsider thefollowing
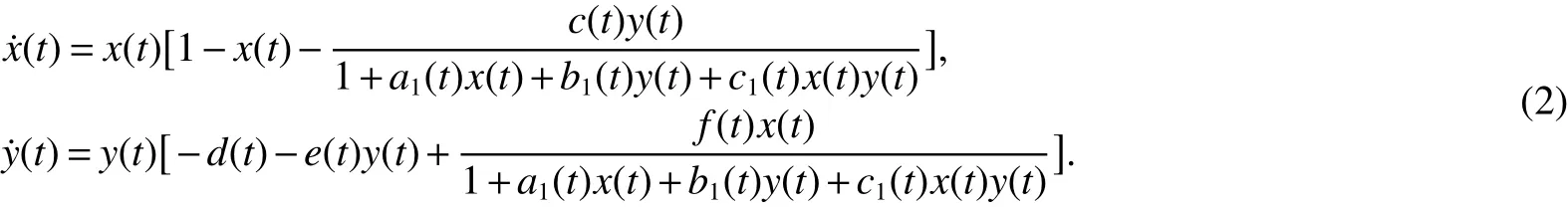
By means of the comparison method and Lyapunov function method we will establish some sufficient conditions on the boundedness,permanence,extinction,the existenceand global attractivity of positiveperiodic solution.
1 Preliminaries
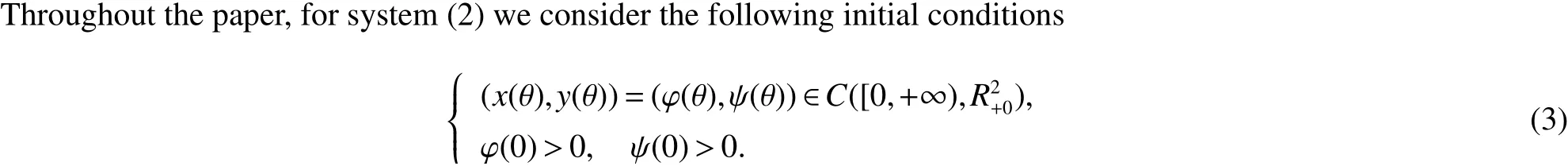
The Banach space C of continuous functions mapping the interval[0,+∞)into
For system(2),we alwaysassume that
(H1) a1(t),b1(t),c1(t),d(t),c(t),f(t)and e(t)are continuous,bounded and strictly positive functions on[0,+∞);
(H2) a1(t),b1(t),c1(t),d(t),c(t),f(t)and e(t)areω-periodic continuouspositivefunctions.
In thispaper,on interval[0,+∞)for any continuousfunction f(t)wedenote
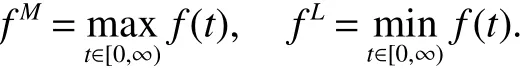
In addition,we will use the following def initionsand lemmas.
Def inition 1[8]System(2)is said to be permanent if there exist positive constants m,M and T0,such that each positive solution(x(t),y(t))of system(2)with any positiveinitial valueφ,fulf ill m1≤x(t)≤M1, m2≤y(t)≤M2for all t≥T0,Where T0may depend onφ.
Def inition 2[9]System(2)is said to be global attractive,if for any two positive solutions(x(t),y(t))and(u(t),v(t))of system(2),one has
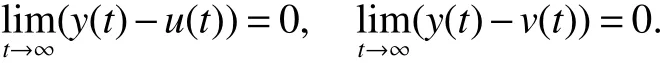
Lemma 1[10]Consider thefollowing equation:
(1)If d1>0,then limt→+∞u(t)=d1/d2;
(2)If d1<0,then limt→+∞u(t)=0.
Lemma 2[10]If there exist positive constants m and M for anysuch that
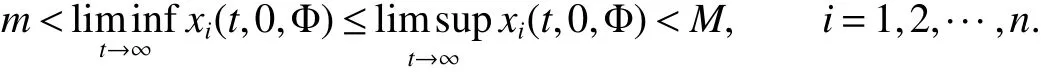
then thefollowing periodic general functional differential equation
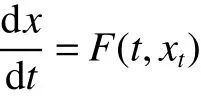
admits at least one positiveω-periodic solution.Where x(t)∈Rnand F(t,xt)is a n-dimensional continuous functional,x(t,0,Φ)=(x1(t,0,Φ),x2(t,0,Φ),···,xn(t,0,Φ))is a solution of the functional differential equation with initial condition x0=Φ.
Lemma 3[11]Let fbe a nonnegative function def ined on[0,∞),such that fis integrable on[0,∞)and uniformly continuous on[0,∞).Then limt→∞f(t)=0.
2 Boundedness,permanence,extinction and existenceof positiveperiodic solution
Theorem 1 Assumethat(H1)holds,then for any positivesolution(x(t),y(t))of system(2)thereexistpositiveconstants M1,M2,such that
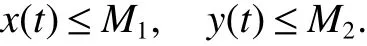
Proof Suppose that(x(t),y(t))be a positive solution of system(2)with initial conditions(3).Firstly,it follows from thef irst equation of system(2)for t>0 that
Consider thefollowing auxiliary equation
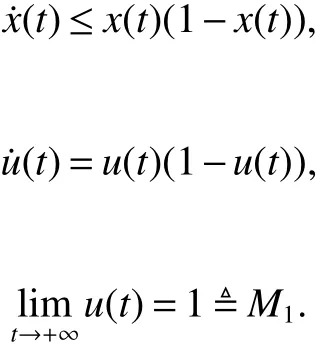
By Lemma1,we derive
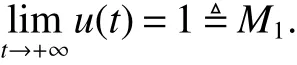
By comparison,there exists a T0>0 such that x(t)≤M1for t≥T0.Next from the f irst equation of system(2)for t>0,we have
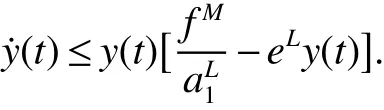
Similar with theaboveway,thereexistsa T1>0 such that y(t)≤M2for t≥T1,
Theorem 2 Assume that(H1)holds and b1M>cL,R>0,then system(5)is permanent.Where
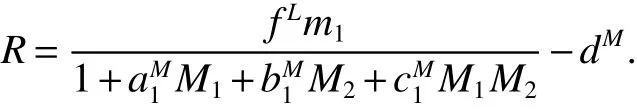
Proof Suppose that(x(t),y(t))be a positive solution of system(2)with initial conditions(3).Firstly,it follows from thef irst equation of system(2)for t>0 that
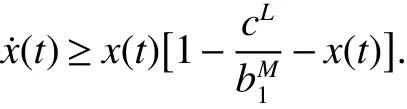
Consider the following auxiliary equation
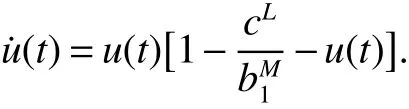
By Lemma1,wederive
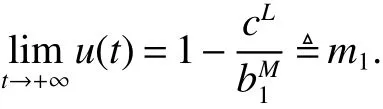
By comparison,there existsa T2>0 such that x(t)≥m1for t≥T2.Next from the f irst equation of system(2)
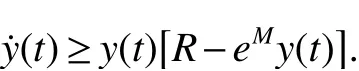
Similar with theaboveway,thereexistsa T3>max{T0,T1,T2},such that y(t)≤m2for t≥T3,
Asasecond result of Lemma1,wehave
Corollary 1 Assume that(H1)holdsandthen predator species Y of system(2)isgo to extinction.
Asa direct result of Lemma 2,from Theorem 2,we have
Corollary 2 Assume that(H2)holds andthen system(2)admits at least one positiveω-periodic solution.
3 Global attractivenessof thesystem
Firstly,for conveniencewedenotethefollowing functionsand notations
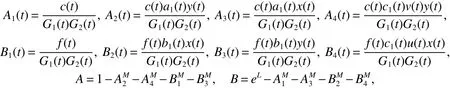
where
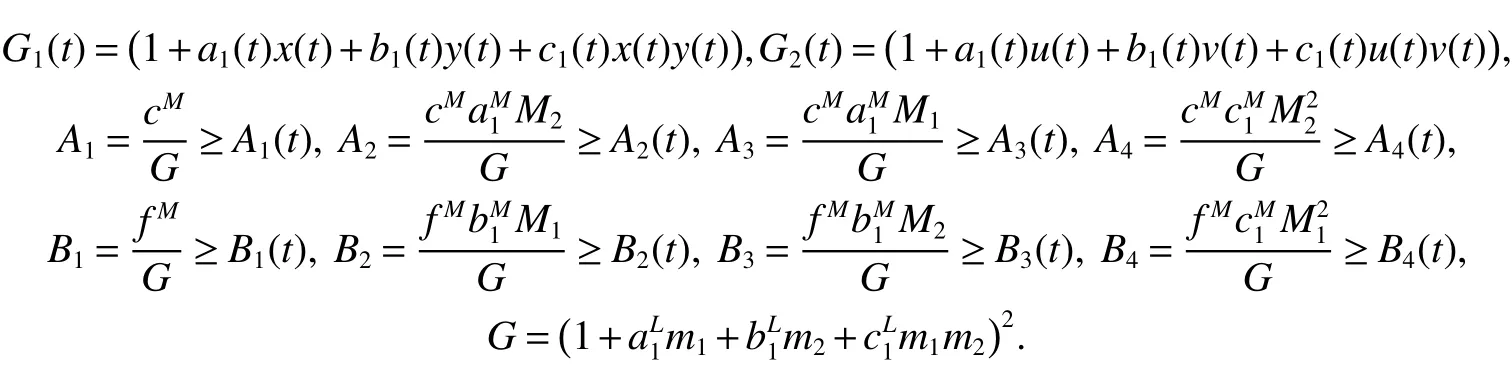
Theorem 3 Suppose that the conditions of Theorem 2 hold and A>0,B>0,then system(2)is globally attractive.
Proof let(x(t),y(t))and(u(t),v(t))beaany two positivesolution of system(2),from thepermanenceof thesolutions,thereexist positiveconstants T>0,mi>0,Mi>0(i=1,2)such that for t≥T
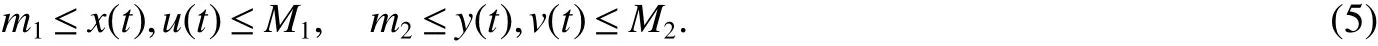
Def ine a Lyapunov function as follows
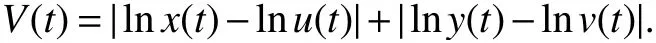
Calculating theupper right derivativeof V(t)along system(2),wehave

Let C=min{A,B},then we have

Integrating from T to t on both sidesof(6)produces
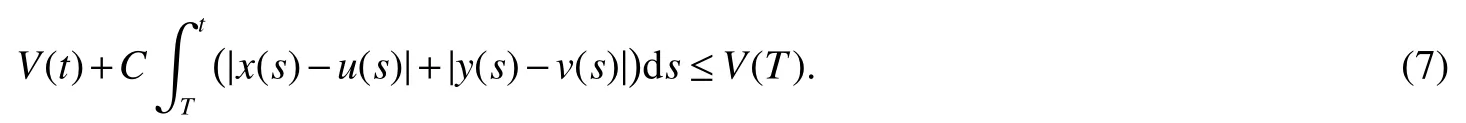
then
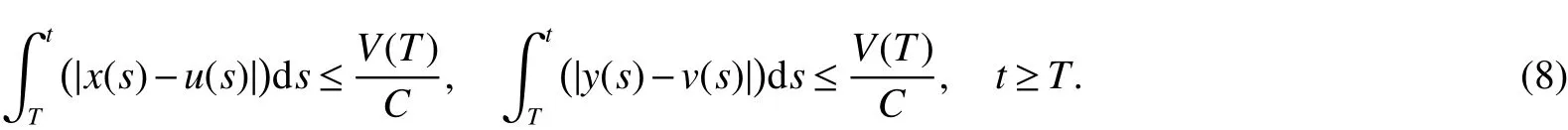
From(5),(7)and(8)we can see that the derivatives˙x(t),˙u(t)and˙y(t),˙v(t)of x(t),u(t)and y(t),v(t)are remain bounded on[T,+∞).Then|x(t)-y(t)|+|u(t)-v(t)|isuniformly continuouson[T,∞).Thusfrom Lemma3,wehave
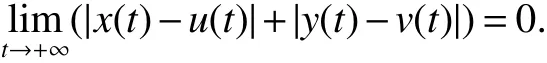
Therefore,
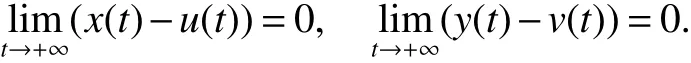
From Corollary 2 and Theorem 3,wehavethefollowing result.
Corollary 3 Supposethat theconditionsof Corollary 2 hold and A>0,B>0,thensystem(2)hasapositiveω-periodic solution which isglobally attractive.
4 Conclusion
In this paper,a class of non-autonomous predator-prey system with Crowley-Martin functional response is discussed.Firstly,by means of the comparison method and inequality estimation method,obtained conditions on the boundedness,permanence,extinction,existence of periodic solution.Secondly,under the condition of permanence and by construction of the Lyapunov functional weobtained some sufficient conditionson theglobal attractivity of thesystems.Themodel and the resultsobtained in this paper can be seen as the extension and supplement of the previously known works[5].
 新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2021年2期
新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2021年2期
- 新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)的其它文章
- Fixed-Time Synchronization of Coupled Memristive Complex-Valued Neural Networks*
- 耦合憶阻復(fù)值神經(jīng)網(wǎng)絡(luò)的固定時(shí)間同步*
- 具有Crowley-M artin功能反應(yīng)函數(shù)的非自治捕食-食餌系統(tǒng)的動力學(xué)行為*
- 二次損失函數(shù)下B-F準(zhǔn)備金的信度估計(jì)*
- 基于納米金/多孔硅基底的熒光標(biāo)記法對生物分子的檢測*
- 某臺循環(huán)水換熱器管束腐蝕分析與防護(hù)*
