Ground-state cooling based on a three-cavity optomechanical system in the unresolved-sideband regime?
Jing Wang(王婧)
College of Physics,Tonghua Normal University,Tonghua 134000,China
Keywords: ground-state cooling,three-cavity optomechanical system,unresolved sideband regime
1. Introduction
As is well known, with the rapid development of microscale integrable devices, cavity optomechanical systems play an important role in quantum information processing.[1–17]A generic optomechanical system consists of a Fabry–P′erot cavity in which one mirror is fixed but the other is free to move around its equilibrium position as a mechanical resonator.[2,3]Using strong pump laser field to drive the cavity field, the effective cavity field length will be changed by the mechanical resonator, resulting in an optical pressure on the mirror which is proportional to the intensity of the trapped cavity field. This mechanism gives the optomechanical coupling between the cavity field and the mechanical resonator.[2,3]In the cavity optomechanical system,researchers can manipulate the cavity field by mechanical resonator to achieve optomechanically induced transparency(OMIT),[2,3]optomechanically induced amplification,[4]coherent perfect absorption or transmission,[5]fast and slow light,[6]optical nonreciprocity,[7,8]etc. The coherent state,[18]superposition state[19]and entangled state[20–22]of mechanical resonator can also be obtained by manipulating a mechanical resonator through cavity field. More recently the sideband scattering engineering has been proposed theoretically and demonstrated theoretically using squeezing, and in particular three different forms of squeezing: (i)injected squeezing,[23](ii)intracavity squeezing,[24](iii)in-loop feedback squeezing.However,the realization of these physical phenomena is based on the premise that the mechanical resonator is cooled to the ground state.
Many different cooling schemes have been proposed to realize the ground-state cooling of mechanical resonators.[25–31]One of the famous cooling methods is sideband cooling.[25]This method requires the condition of the resolved sideband regime,where the mechanical resonator resonance frequency is higher than the cavity field decay rate.[25]In practice, it is a challenging task to satisfy this condition for a typical mechanical resonator whose frequency is in the range of kHz–MHz. Therefore, it is particularly important to realize ground-state cooling of mechanical resonator in the unresolved sideband regime, in which the cavity field decay rate would be larger than the resonance frequency of the mechanical resonator. In recent years, researchers have made some achievements in the unresolved sideband regime. For example,the electromagnetically induced transparency(EIT)-like cooling mechanism. It is based on quantum interference cooling mechanical resonator to its the ground state.[26]Guo and Li[26]propose to cool a mechanical resonator close to its ground state via an EIT-like cooling mechanism.With the help of the auxiliary cavity field whose decay rate is less than the frequency of the mechanical resonator,the cooling process of the double-cavity optomechanical system corresponds to the maximum value of the optical fluctuation spectrum and the heating process corresponds to the minimum value of the optical fluctuation spectrum by selecting the optimal parameters.Results show that the cooling effect of the double-cavity optomechanical system is better than that of the standard cavity optomechanical system, even it can be cooled to the groundstate cooling. Inspired by Ref. [26] we naturally ask a question: Can ground-state cooling of a mechanical resonator be achieved in a multi-cavity optomechanical system? Can the multi-cavity optical mechanical system bring new insights into the ground-state cooling of a mechanical resonator?
In this paper, under the unresolved sideband condition,we address the above questions by investigating the groundstate cooling of a mechanical resonator via an EIT-like cooling mechanism in a three-cavity optomechanical system. The three-cavity optomechanical system under consideration is schematically shown in Fig.1. The system includes 3 cavity fields labeled by c1,c2,and c3. We let only c1interact with the mechanical resonator by radiation pressure. Thus c1forms a standard optomechanical subsystem. Two adjacent cavities are coupled to each other. In addition,c1is driven by a pump laser field. In the system we consider, there are two different quantum interference effect channels. One is from c1–c2coupling and the other is from c1–c3coupling. Two different quantum interference effect channels satisfy the condition of two-photon resonance, respectively. By modifying the quantum interference, the cooling process can be enhanced while the heating process can be suppressed,so that the ground-state cooling of mechanical resonator can be realized. It should be noted that the results obtained are similar to Refs. [26–28].However, this study is different from Ref.[26–28]. First, the physical model is different. The physical model of Ref.[26]is a double-cavity optomechanical system,the physical model of Ref.[27]is a double-Lagureer–Gaussian-cavity optomechanical system,while the physical model of Ref.[28]is a doublecavity optomechanical system containing an atomic ensemble.Our scheme is to realize the ground-state cooling of the mechanical resonator in the multi-cavity optomechanical system.Second,in Ref.[26],the auxiliary cavity field must be a good cavity field, while in our scheme, the auxiliary cavity fields can be bad cavity fields. Third,the additional auxiliary cavity fields not only change the quantum interference effect channels,but also have more adjustable parameters,which can better adjust the cooling effect. Here instead of only illustrating the ground-state cooling of mechanical resonator in such a system,we are especially interested in what roles the c1,c2,c3could play. It is also helpful for realizing the physics of the three-cavity optomechanical system. Fourth, our scheme can make the mean phonon number close to zero in a larger range of parameters.

Fig.1. The schematic of a three-cavity optomechanical system. Three cavities connected through tunneling parameters J12 (J13). A strong pump light field is injected into cavity c1 while cavity c1 is coupled with mechanical resonator b.
The paper is organized as follows. Firstly, we introduce the theoretical model, the detailed analytical expressions of the system, obtain the steady-state mean values, and discuss the final mean phonon number. Secondly, we study in detail the ground-state cooling of mechanical resonators by tuning the system parameters and provide the corresponding physics explanation. Lastly,we summarize our work.
2. Model and equations
We consider a hybrid system,composed of three cavities cj(j=1,2,3), a mechanical resonator b, as shown in Fig.1.The c1is coupled to the mechanical resonator via the radiation pressure force. Furthermore, c1is directly coupled to c2(c3). The c1is simultaneously driven by a single-frequency continuous-wave classical input field, which is called the pump laser field. Firstly, by setting ˉh=1, the total Hamiltonian of this hybrid system in the presence of a pump laser field can be written as an added mechanical resonator free term and optomechanical interaction on the basis of ordinary cavity Hamiltonian,i.e.,[32–36]

where ?11=ω1?ωL, ?2=ω2?ωL, and ?3=ω3?ωLare the detuning of the j-th(j=1,2,3)cavity field frequency with pump laser field frequency. Note that the same cavity resonance frequencies ω1=ω2=ω3lead to the same detuning?11=?2=?3.
According to the Heisenberg equation and the commutation relation,the temporal evolution of the operators c1,c2,c3and b can be obtained. Taking the decay terms into consideration,we can obtain the Heisenberg equations as follows:


Defining the steady solution of the cavity field and mechanical resonator as Cj(j=1,2,3) and B, respectively, by solving Eq.(3),we can obtain the steady solutions as follows:

where ?1=?11?g0(B?+B)is the effective detuning between the c1and the the pump field, including the frequency shift caused by the mechanical resonator motion.
Generally, in the case of strong pump laser field, linearizing the operators around the steady state values as cj=Cj+δcj(j =1,2,3), b=B+δb. Neglecting the constant and higher-order terms with|C1|?1,Eq.(3)then becomes
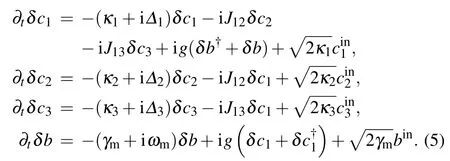
The g=g0C1is the enhanced effective optomechanical coupling coefficient.
We can make an inversion based on Eq.(5)and obtain the following Hamiltonian:

In the regime g ?ωm, we can ignore the back actions of the mechanical resonator. Therefore, in Eq. (6), the effective Hamiltonian for cooling reads

The Heisenberg equations of Hamiltonian(7)are presented as follows:

We define the radiation force as[26–28]

The optical force fluctuation spectrum for this force is[26–28]

By introducing the Fourier transform of the operators

we can obtain the following two important properties of Fourier transform:


We can reach
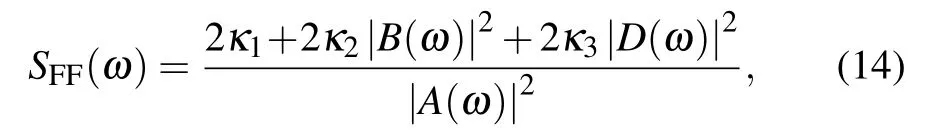
where

If we further simplify SFF(ω),we can obtain

The rate equation for the phonon on the mechanical resonator is given by [26–28,38]



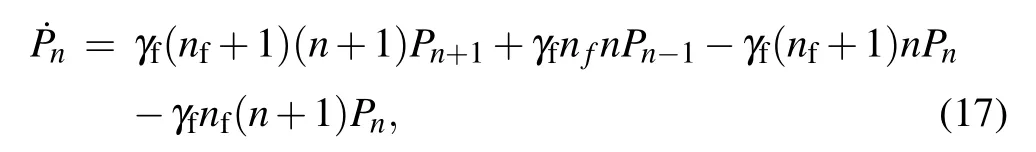
where γfis the rate at which the average phonon number tends to the steady value B?B,which satisfies

nfis the final mean phonon number of the mechanical resonator. If nf<1,it should be considered that the mechanical resonator is cooled to the ground state. Solving Eq.(18), the nfcan be obtained as

where

The nfis mainly determined by the γm,nm,γcand nc;γcis the cooling rate and ncis the quantum limit of cooling. If γm→0,then nf→nc. This means that the nfwill have a non-zero lower limit nceven if there is no heat reservoir. In order to obtain very small nf, a large cooling rate γcand a small cooling limit ncmust be satisfied. The γcand ncare determined by the positive-frequency and negative-frequency parts of the optical fluctuation spectrum, i.e., SFF(±ωm). We also note that the negative frequency part of the SFF(?ωm)associated with transition rate Γn+1←ndetermines the heating process, while the positive frequency part of the SFF(ωm) associated with transition rate Γn←n+1determines the cooling process. Therefore,in order to make the mechanical resonator cooling close to its ground state, it is necessary to suppress the heating process and to strengthen the cooling process.
3. Ground-state cooling of mechanical resonator
We hope that the ground-state cooling of the mechanical resonator can be achieved in the unresolved sideband regime by introducing the auxiliary cavities(the second and third cavity field), although the auxiliary cavities and the mechanical resonator are indirectly related. Thus in this section, we describe in detail how the auxiliary cavities impact the optical fluctuation spectrum.
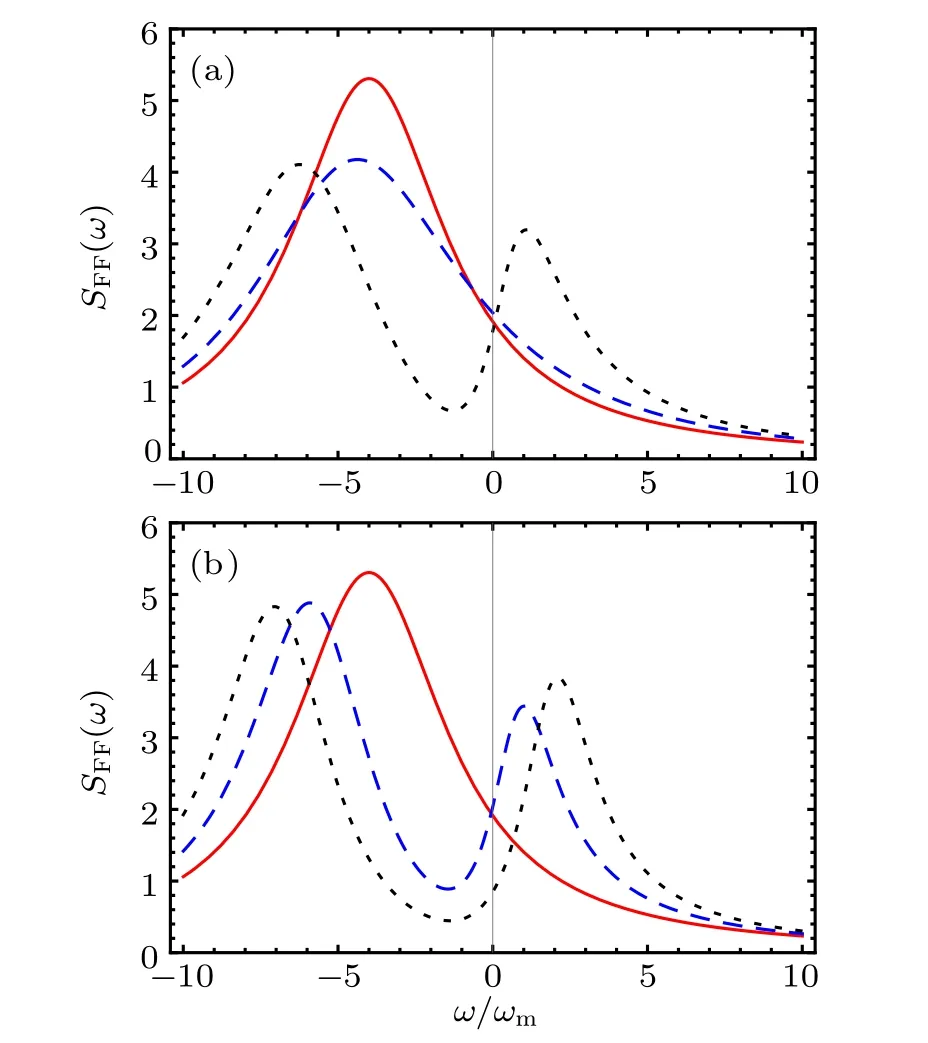
Fig.2. The optical fluctuation spectrum SFF(ω)(in arbitrary units)versus the frequency ω: (a) κ2 =10ωm, (b) κ2 =0.7ωm. Three cases are shown with different colors: (i) the red solid curve shows the J12=J13=0,(ii)the blue dashed curve shows the J12=3ωm,J13=0,(iii)the black dotted curve shows the J12 =3ωm,J13 =3ωm. The values of the other parameters are set as ?1 =?4ωm, ?2 =?3 =?ωm,κ1=3ωm,κ3=0.5ωm.
We first analyze and discuss the influence of decay rate of cavity field c2on the ground-state cooling of mechanical resonator. In Fig.2, from top to bottom, we draw the optical fluctuation spectrum SFF(ω)versus the frequency ω when c2is bad cavity field and c2is good cavity field. It is well known that the decay rate determines the quality factor of the cavity field. For c2in the bad cavity field case, we adopt the decay rate κ2=10ωmin Fig.2(a). For c2in the good cavity field case plotted in Fig.2(b), we have adjusted c2to the decay rate of κ2=0.7ωm. For comparison, three cases are plotted for each the optical fluctuation spectrum SFF(ω):(i) the red solid curve show the J12=J13=0, (ii) the blue dashed curve show the J12=3ωm, J13=0, (iii) black dotted curve show the J12=3ωm, J13=3ωm. It should be emphasized that under any circumstances, c1works in the unresolved sideband regime, i.e., the decay rate of c1is much larger than the frequency of b(κ1>ωm). Let us first see the red solid line of Figs. 2(a) and 2(b). When c2(c3) is decoupled from c1(J12=J13=0 ), no matter whether c2is good or bad, the profile of the SFF(ω)has a Lorentzian shape with a single peak located at ω =?1=?4ωmand the half width of the peak being κ1. The values of SFF(?ωm) and SFF(ωm)are very close. According to the second part of the paper,we know that the optical fluctuation spectrum SFF(?ωm) represents the heating process and the optical fluctuation spectrum SFF(ωm)represents the cooling process,and nf>1,so it is impossible to cool the mechanical resonator in the ground state only when c1exists. Next, let us see the blue dashed curve(J12=3ωm,J13=0). When c3and c1are decoupled,if c2is a bad cavity,the optical fluctuation spectrum SFF(ω)will still be a Lorentzian shape [see Fig.2(a)]. On the contrary, when c2is a good cavity, we must point out that the system at this time is consistent with Ref.[26],the optical fluctuation spectrum SFF(ω) becomes distorted, the single Lorentzian peak splits into two asymmetric narrow peaks and a dip emerges between them[see Fig.2(b)]. The peak on the right hand is in the positive-frequency part of the optical fluctuation spectrum,and the dip is in the negative-frequency part of the optical fluctuation spectrum. The values of SFF(?ωm) and SFF(ωm)are very different, and nf<1, that is to say, the asymmetric heating and cooling rates make it possible to realize groundstate cooling of mechanical resonator. It is noteworthy that the dip is caused by EIT.[26–28]Finally,let us see the black dotted curve. When c2and c3are present (J12=3ωm, J13=3ωm),no matter whether c2is bad (Fig.2(a) κ2=10ωm) or good(Fig.2(b) κ2=0.7ωm), the ground-state cooling of the mechanical resonator can be achieved. By comparing Figs. 2(a)and 2(b), the following results can be obtained: due to the introduction of the two auxiliary cavities (both cavities are good or only one of them is good), the mechanical resonator can be successfully cooled to the ground state beyond the resolved sideband condition. At the same time, we also find that participation of the third cavity field can make the cooling mechanism become more efficient in the unresolved sideband regime. Therefore, we can use the method of increasing the number of cavity field to enhance the cooling effect,while to overcome the heating effect.
In the following, we focus on optimal cooling regime when κ2>ωm. From Heisenberg Eq.(8),we have


In Fig.3 we plot the optical fluctuation spectrum SFF(ω)as a function of the frequency ω for different tunnel decay rate κ3: κ3=2ωm(red solid curve),κ3=ωm(blue dashed curve),κ3= 0.5ωm(green dot-dashed curve), κ3= 0.05ωm(black dotted curve). Here we choose J13=3ωmand ?1=?4ωm,which means that the optimal coupling strength between the c1and c2is J12= ωm. Under the optimal condition, from Fig.3,we can see that the dip of the optical fluctuation spectrum SFF(ω) is at ω =?ωmand the peak on the right hand is at ω =ωmeven if κ3=2ωm. With the decrease of decay rate κ3,SFF(ωm)is further enlarged,and SFF(?ωm)is further suppressed. This is due to the fact that the quantum interference of c1-c3coupling inhibits the heating process. According to Eq.(21),the larger the SFF(ωm),the smaller the SFF(?ωm),and the better the effect of the ground-state cooling. With decreasing values of decay rate κ3to 0.05ωm, the optical fluctuation spectrum value for the heating process can reach zero completely(SFF(?ωm)?0),the cooling process can reach its maximal value (SFF(ωm)=5). This means that in the threecavity system, the smaller decay rate κ3is more suitable for ground-state cooling the mechanical resonator.

Fig.3. The optical fluctuation spectrum SFF(ω) (in arbitrary units)versus ω, for κ3 = 2ωm (red solid curve), κ3 = ωm (blue dashed curve),κ3=0.5ωm (green dot-dashed curve),κ3=0.05ωm (black dotted curve).Here,κ2=10ωm,J13=3ωm,J12=.For the other parameters see Fig.2.
Figures 2 and 3 highlight the key role of the decay rate κ2,3in observing the ground-state cooling phenomena. In order to accurately explain the effect of decay rate κ3on the ground-state cooling of the mechanical resonator,we plot the optical fluctuation spectrum SFF(ω) as a function of decay rate κ3at ω = ?ωm(red curve) and ω = ωm(blue dashed curve) in Fig.4. It is found that the heating effect monotonously increases with the decay rate κ3,the cooling effect is just the opposite. In the regime 0 <κ3<3ωm,we have SFF(?ωm)<SFF(ωm), whereas SFF(ωm)<SFF(?ωm) when 3ωm<κ3<4ωm. Therefore,in order for the ground state of the mechanical oscillator to be good, the decay rate κ3must be small enough. This is consistent with Fig.3.
Figure 5 shows the variations of the cooling rate γcas a function of J13.The red curve κ3=0.01ωm,blue dashed curve κ3=0.5ωm, green dot-dashed curve κ3=2ωm. As you can see from Fig.5,if you want to cooling rate faster,the value of κ3will be smaller.
Figure 6 shows the variation of the steady-state final mean phonon number nfof the mechanical resonator as a function of J13. One can clearly see that the nfcan be less than 1. This means that mechanical resonator can be cooled nearly to its ground state, even in the usual unresolved sidebands, due to the presence of the auxiliary cavities.

Fig.4. The optical fluctuation spectrum SFF(ω) (in arbitrary units)versus κ3 with ω =?ωm (red solid curve) and ω =ωm (blue dashed curve). For the other parameters see Fig.2.

Fig.5. The cooling rate γc as a function of J13 in the case of ?1 =ωm ?for three different κ3 with κ3 =2ωm (green dotdashed curve),κ3=0.5ωm(blue dashed curve),κ3=0.01ωm(red solid curve).Here ωm=4π×10×106 Hz,g=0.2ωm. For the other parameters see Fig.2.

Fig.6. The mean phonon number nf as a function of the J13 in the case of ?1 = ωm ?for J12 = γm. Here γm = 5π×102 Hz,g0=1.6×10?4ωm,EL=6000ωm. For the other parameters see Fig.2.
4. Conclusions
We have studied the ground-state cooling of the mechanical resonators in a coupled cavity optomechanical system.The optical fluctuation spectrum can be modified by quantum interference effects induced by the c1–c2and c1–c3couplings. Because of the combination of two quantum interference effects,by selecting the optimal parameters, the cooling process of the mechanical resonator corresponds to the maximum value of the optical fluctuation spectrum, and the heating process corresponds to the minimum value of the optical fluctuation spectrum,which finally cools the mechanical resonator.
- Chinese Physics B的其它文章
- Statistical potentials for 3D structure evaluation:From proteins to RNAs?
- Identification of denatured and normal biological tissues based on compressed sensing and refined composite multi-scale fuzzy entropy during high intensity focused ultrasound treatment?
- Folding nucleus and unfolding dynamics of protein 2GB1?
- Quantitative coherence analysis of dual phase grating x-ray interferometry with source grating?
- An electromagnetic view of relay time in propagation of neural signals?
- Negative photoconductivity in low-dimensional materials?

