An electromagnetic view of relay time in propagation of neural signals?
Jing-Jing Xu(徐晶晶), San-Jin Xu(徐三津), Fan Wang(王帆), and Sheng-Yong Xu(許勝勇)
1School of Microelectronics,Shandong University,Ji’nan 250100,China
2Department of Electronics,School of Electronics Engineering and Computer Science,Peking University,Beijing 100871,China
Keywords: neural signal relay,propagation velocity,electromagnetic field model,ion channels
1. Introduction
Myelinated axons have much longer distances(~1 mm)between neighboring nodes of Ranvier than unmyelinated axons. Individual neural signals, known as “action potentials”(APs),can be measured locally at these nodes along the myelinated axons, which appear as voltage peaks, using sophisticated instruments with manmade circuits and amplifiers. In a living biosystem, however, it is unclear exactly what exact physical information is transmitted when an AP propagates along an axon. And to physicists in particular, how such an electric signal can be transmitted in a complicated matrix of water and bio-materials. These fundamental questions have attracted increasing attention in recent years. New models and hypotheses,such as the quantum information model based on neural microtubule structures,[1,2]the electromechanical soliton model,[3,4]and the electromagnetic field model,[5–7]have been presented. These new models not only represent the development of the widely accepted Hodgkin–Huxley (HH)equations,[8,9]which faces difficulties in explaining the phenomena of saltatory conduction, but also offer alternative approaches to better understanding the brain functions and even create novel artificial intelligence.
When a neural signal propagates along a myelinated axon, the total time spent can be divided into two parts: the delay time on the transmission path,and the delay time in the signal relay process,which is usually referred to as relay time.There are two perspectives for explaining the relay: saltation with respect to space,and saltation with respect to time. With respect to space, the transmission time of neural signals is mainly spent along the path of internodal segments.[10]This point has been further developed to support the electromechanical soliton model, in which neural mechanical dense waves propagate via the density change of axonal membrane.[4,11,12]However,other models like the classical cable model and electromagnetic field model support the electrical nature of nerve signals,[6,9]which transmit at a fraction of the speed of light(c)according to Maxwell equations. Therefore,the delay time on the transmission path is negligible as compared with the relay time.
The cable model emphasizes the low-frequency property of neural signals,which propagate via the local transverse current field along the inner surface of cable-like axons.[9]For myelinated axons, the distance between two neighboring signal sources,i.e.,Ranvier nodes,can be as long as several millimeters. This distance is much longer than the extent of the local transverse electric field resulting from sodium ions(positive ions),which is calculated to be on the order of only 10μm due to the screen effect in an electrolyte solution.[13,14]New experimental evidence recently published does not support this model,either.[3]
The electromagnetic field model[7,15,16]states that neural signals are electromagnetic wave-like pulses, propagating via the naturally formed dielectric waveguides in biosystem.These neural waveguides follow the structure of “intracellular fluid – lipid membrane (e.g., myelin sheath in myelinated axons) – extracellular fluid”.[7]Compared with conventional metal waveguides,these neural softmaterial waveguides have limited transmission efficiency for electromagnetic fields, resulting in an attenuated electric field strength over distance.[5,6]This model could explain the conduction of neural signals in both unmyelinated and myelinated axons, and even non-neural biological structures, such as endoplasmic reticulum,[17]vascular bundle in plants,[18,19]and singlecell organisms,such as the paramecium.[20]
The up-to-date unclear relay process in neural conduction is important for better understanding the transmission mechanism of neural signals. In this study, previously published experimental data on neural signal conduction speed in myelinated axons are reanalyzed, and show that a very short relay time occupies only a small portion of the whole peak duration,indicating that neural signals along a myelinated axon overlap temporally. Accordingly,we schematically develop the physical process of neural electromagnetic signals’relay on nodes,and explain the relationship between neural signals and APs,and that between relay time and superficial propagation speed by using the electromagnetic filed model. Furthermore,neural signals’transmission on unmyelinated axons can be explained well with this mode,and the distribution of Na+ion channels is guessed, too. We conclude that the electromagnetic field model is useful.
2. Materials and methods
2.1. Calculation method
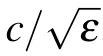

where ?L is the distance and ?T is the total relay time between two testing points. The ?L can be rewritten as

where Linis the average internode length in a myelinated axon,and N is the number of Ranvier nodes between the two testing points. Similarly,?T can be rewritten as

where τ is the average relay time spent at each node. Thus,τ can be expressed as

2.2. Data sources
All data used in the present study were obtained from the papers published between 1966 and 2018 to minimize the data bias. Studies were performed on myelinated axons in different animals, namely the vagus and aortic nerves in cats, sciaticgastrocnemius in frogs, tibial nerves in white rabbits, the L5 motor,and sensory roots in mice.These experiments were performed in Delhi, Maryland, Edinburgh, California, and Missouri University,respectively.[22–27]In one of the papers,two sets of data seemed to be confused and the original authors’clarification supported their validity.
3. Results
3.1. Relay time of neural signals in myelinated axons
Using Eq. (4), the general values of τ from reported experimental data[22–27]were calculated, and the results are listed in Table 1.The calculated values of τ range from 16.3μs to 87.0 μs. These values are consistent with experimental and/or computational results, where a relay time in a range of 1 μs–100 μs was termed interval time,[28]internodal conduction time,[29,30]elapsed time,[31]or latency.[32]
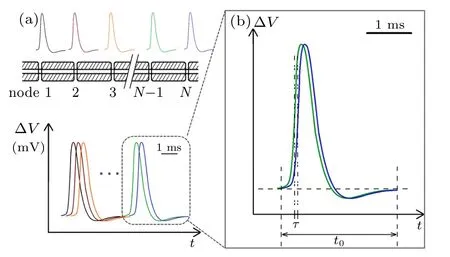
Fig.1. (a)Schematic diagram of myelinated fibers and their action potentials in the same timeline,and(b)time shift of two neighboring action potentials.
Two experimental observations are recorded. One is that the APs recorded at different nodes are almost identical along the same axon, with a duration of about 2 ms;[33]the other is that the relay time is less than 100 μs per node as shown in Table 1. These two observations unambiguously indicate that the APs measured at neighboring nodes were temporally overlapping as shown schematically in Fig.1. The enlarged box (Fig.1(b)) provides a close look at two peaks from two neighboring nodes,where the shift from the blue curve to the previous green curve represents the relay time τ. The calculated τ shown in Table 1 is only ~0.8%–4.4%of the measured average duration t of APs(≈2 ms).

Table 1. Calculation results of average signal relay time τ per node.
The overlap of two successive APs indicates that at the rising edge of the initial period of one AP, the voltage-gated ion channels of the neighboring node are already activated and open to generate a new AP.It is determined that the fastchanging electric fields are responsible for transmitting the signals to the next node to activate the gated ion channels.
3.2. Signal relay process at Ranvier nodes
The electromagnetic field model emphasizes the transient,pulsed characteristics of neural signals,and supports the concept of softmaterial waveguides as the transmission pathway. Based on the above calculations,the relay of neural signals along the myelinated axons can be described schematically by the electromagnetic field model.
Figure 2 illustrates the origin of signal relay time τ between two neighboring nodes, named node 1 and node 2. A typical ?V–t curve measured at node 1 is plotted in Fig.2(a).As is well known, there exists a threshold point Vthresholdat t =t0, beneath which the local ion channels at node 1 are closed.[33]At this time, the ion channels at node 2 are also closed, but it is worth noting that the ion channels at node 2 have sensed an attenuated electric field from node 1. Due to the limited transmission efficiency of neural softmaterial waveguides, the electric field rising at node 1 attenuates a lot by the time it reaches node 2.
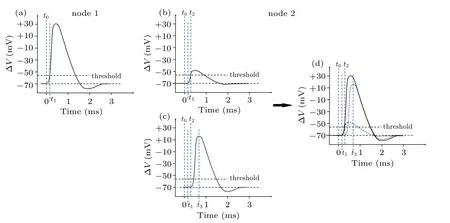
Fig.2. Schematic diagram of the origin of delay time per node,showing(a)measured transmembrane potential change at node 1,(b)attenuated potential change at node 2, which is transmitted from node 1, (c) transmembrane potential change due to opening of ion channels at node 2, (d) shape of action potential at node 2, a small portion of which is caused by pulse generated by ion channels at node 1(b), a large portion of which is caused by pulse from local ion channels(c)once attenuated pulse reaches the threshold.
Figure 2(b)illustrates this attenuated signal at node 2. As the transmembrane ion current increases its strength at node 1,resulting in an abrupt increase of the local electric field,the signal amplitude sensed at node 2 increases rapidly at the same time.When it reaches the threshold,the ion channels at node 2 open(t=t2)and subsequently generate their own local pulsed signal as shown in Fig.2(c). Note that the curve in Fig.2(b)starts from time t,while the curve in Fig.2(c)starts from time t2. Therefore,the whole ?V–t curve in Fig.2(d),recorded as action potential at node 2,is actually an overlap of two curves:one is from the attenuated signal transmitted from node 1,and the other is generated by local ion channels at node 2,which is almost identical to that at node 1. In short,τ =t2?t1,where t1and t2are the opening times for node 1 and node 2,respectively.
Figure 2 illustrates the differences among three temporal terms: the relay time per node, the opening time of the ion channels,and the duration of the AP.This is helpful in understanding the propagation process of neural signals. The relay time per node, τ, includes two parts: a negligible transmission time along the internodal segment, and the waiting time prior to node 2 sensing an attenuated field higher than its activation threshold. Note that the calculated range of 16.3μs–87.0μs for τ is close to the reported activation time constant of voltage-gated sodium channels at 100 kHz, 64±6 μs.[34]This indicates the correlation between the relay process and the activation of ion channels.
The opening time of ion channels,i.e.,t3–t2in Fig.2,referring to the duration that the channels remain open, is estimated at 0.4 ms–1.0 ms.[33]A full AP peak includes the below-threshold period,the depolarization period(i.e.,activation of sodium channels and the following inwards ion flux),the repolarization period(i.e.,inactivation of sodium channels and activation of potassium channels),and the recovery period(i.e., returning to normal permeability via sodium-potassium ATPase pumps).
4. Discussion
Our data indicate that the“signal”that transmits along an axon is not a full peak of “action potential”, but an electric field perpendicular to the membrane surface variable in space.This scenario of neural signal propagation was occasionally illustrated by data in early reports,but seems to have been overlooked for a long time. It is possible that protein ion channels respond to this field like a dipole in a shock wave,twisting or shifting their chain of peptides,resulting in an open conformation of the central nano-channel, but this is beyond the scope of this study. We discuss below how the relay process affects the speed of the propagation of neural signals,how this speed differs in different axons,and whether this model is applicable to unmyelinated axons.
4.1. Relay time and superficial propagation speed on myelinated axons
The measured propagation speeds of the neural signals,e.g.,30 m/s–100 m/s in myelinated axons,are actually nominal speeds,rather than the true transmission speeds of electromagnetic fields that are the real physical form of neural signals. It is well clarified that the measured propagation speed of APs on a myelinated axon is determined by the number of Ranvier nodes per unit length. For an axon with fixed length,a longer internode length Linresults in a smaller number of nodes,thus a smaller total signal delay.[24,25,35,36]
However, when Linis too large, the electric field attenuates too much to reach the threshold for triggering the ion channels at neighboring nodes. Therefore, in a live biosystem, these elements must be in balance. As a result, longer Linvalues are usually observed in systems with thicker myelin sheaths,which increases the transmission efficiency of signal,[5]or larger number/density of ion channels(~1000/μm2) at Ranvier nodes,[37]which leads to stronger signals, or both. The lengthening of the internode length is primarily achieved by thickening the myelin sheath. According to the electromagnetic field model,the myelin sheath serves as the guide layer in the pathway of softmaterial dielectric waveguides; thicker dielectric layers have been experimentally proven to lead to lower attenuation, and thus longer effective transmission length(the distance of propagation when the signal’s intensity attenuates to 1/e of its original value),for the electromagnetic signals.[5]In practice,the positive correlation between internode length and fiber diameter,in which the myelin sheath plays a decisive role,is also widely reported.[38,39]
As a result, myelinated nerves usually adjust the thickness of the myelin sheath to change the internode length for determining the speed of neural signal transmission,from the perspective of electromagnetic field model.
4.2. Is electromagnetic field model valid in describing transmission of neural signals along unmyelinated axons
In the evolution of living organisms, myelinated axons develop from unmyelinated axons. Therefore, it is reasonable to hypothesize that the propagation of neural signals in both unmyelinated and myelinated fibers share some common mechanisms.
The model of signal relay in myelinated axons may be applied to the propagation of neural signals in unmyelinated axons.According to the typical velocity(1 m/s)of neural signals in unmyelinated axons, the conduction time is 1 second for a one-meterlong fiber. If the relay time is 10 μs, there would need to be 105nerve signal relay sites, i.e., 105ion channels or channel clusters distributed along this one-meterlong axon.Therefore, the distance between two adjacent sites, l, can be calculated to be 10μm,consistent with the reported values of 5μm–15μm.[40,41]
Three distribution patterns are suggested for voltagegated ion channels along unmyelinated axons as shown in Fig.3. The first pattern is a uniform distribution, where the ion channels are separated approximately even spaced as reported by Black et al.[42]This spacing should be as long as possible, thereby increasing the propagation speed of neural signals,yet not be so long that the next channel cannot receive a strong enough activation signal. Obviously,when the original signal’s strength increases, a longer spacing between two channels is favored. As a result, the clusters of ion channels at the signal source very likely represent a better distribution along the axons, such as point clusters or ring-like clusters.More and more evidence has indicated a cluster distribution of ion channels;[43,44]for example,Johnston et al. found that Na+ion channels are localized in clusters, and the distance between them is about 5 μm–15 μm in the aplysia axonal membrane.[45]
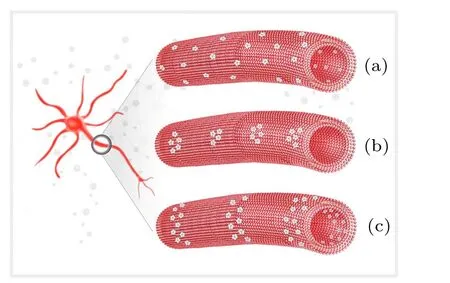
Fig.3. Three possible distribution patterns of voltage-gated ion channels along unmyelinated axons, showing(a)uniform distribution, (b)point cluster pattern,and(c)ring-like pattern.
Due to the uniform attenuation of neural electromagnetic signals in unmyelinated axons where the dielectric layer is only one single lipid bilayer,the average spacing l could only be determined by the number,M,of ion channels at one signal source. One feasible way to increase M is to enlarge the diameter of the axon;previous experiments demonstrated that there are usually more ion channels on thicker axons.[46]Other studies have also reported that thicker axons usually have larger clusters,[47]and thus more sodium ion channels occur at signal sources. This may explain why thicker axons usually demonstrate higher conduction speed of neural signal.
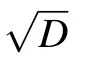
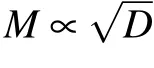
5. Conclusions
In this study,addressed is the exact physical information that is transmitted when action potentials propagate along an axon in a live biosystem. By revisiting the data obtained from experiments on myelinated axons over the past five decades,we conclude that the action potential peaks generated at neighboring Ranvier nodes are highly overlap temporally for transmission events in a myelinated axon,with a shift of only tens of microseconds,a few percents of the average duration of an action potential peak. The overlap of neural peaks directly indicates that the exact physical information transmitting along an axon is not a whole peak,but only the rising electric field,E,caused by the transient transmembrane ion current. Before this electric field reaches its maximum value,the neighboring ion channel has already been opened and begun to generate its own local peak of the electric field. The shift,defined as relay time τ in this work, is attributed to the waiting time for ion channels of rising electric field to reach the threshold.
This mechanism can be used to explain the propagation process of neural signals in unmyelinated axons. It also strongly argues for the modification of our models of the triggering mechanism of so-called voltage-gated ion channels.Furthermore,the whole picture may help to better understand the working mechanisms of synapse connection among neurons as well as various brain functions.
- Chinese Physics B的其它文章
- Statistical potentials for 3D structure evaluation:From proteins to RNAs?
- Identification of denatured and normal biological tissues based on compressed sensing and refined composite multi-scale fuzzy entropy during high intensity focused ultrasound treatment?
- Folding nucleus and unfolding dynamics of protein 2GB1?
- Quantitative coherence analysis of dual phase grating x-ray interferometry with source grating?
- Negative photoconductivity in low-dimensional materials?
- RF magnetron sputtering induced the perpendicular magnetic anisotropy modification in Pt/Co based multilayers?

