Xuefeng Wei(韋學(xué)鋒) and Yanting Wang(王延颋),?

1CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: protein folding,2GB1,two-state model,folding nucleus

1. Introduction

Protein folding is a molecular process in which a polypeptide chain with a designated sequence of amino acid residues forms a compact and well-defined three-dimensional structure via self-assembly, which is an important and challenging problem in biophysics, statistical mechanics, and computer simulation.[1]With the development of computational techniques,computer simulation of the protein folding process can reach a temporal scale as long as milliseconds for small proteins.[2]Because protein is a complex asymmetric molecular system with complex interactions among different components, the folding process is determined not only by local interactions between neighboring amino acid residues along the chain, but also by global non-native contacts.[3,4]Hundreds of experimental and computer simulation methods have been proposed to understand details of the underlying folding mechanism. However,it has been shown that the complete folding pathway of a single protein is extremely difficult to be experimentally determined,[2]while conventional all-atom molecular dynamics(MD)simulation methods cost a huge amount of computing resource to simulate the folding process of even a very small protein with less than 100 amino acid residues,[5–7]and it is currently impossible to directly simulate a little larger ones. Therefore, many accelerated simulation methods, such as the replica-exchange MD simulation method,[8]have been applied to simulating protein folding processes.

On the other hand, many theoretical models, such as the Go model,[9]have been proposed to describe and predict protein folding dynamics, but none of them can serve as a general theory explaining all aspects of protein folding phenomena.[10–12]Nevertheless,most of these models rely on the concept of a funnel-shape multidimensional free-energy landscape,[4,13,14]which conceptually describes the way proteins reliably fold into their energetically most favorable conformations.However,it is always difficult to depict the funnelshape free energy landscape quantitatively, partially because the reaction coordinates of this funnel are unknown. The funnel-shape free energy landscape is rugged, so the protein has to overcome multiple barriers as well as to cross the intermediate state before reaching the thermodynamically stable native state. For some small proteins with a simple folding process,there is only one major energy barrier between the native and non-native states, and folding/unfolding roughly exhibits a two-state process. The sub-structure responsible for the transition of the whole protein on top of the free energy barrier is called “folding nucleus”. For such small proteins,we may regard unfolding as the reverse process of folding,so high-temperature unfolding MD simulation,which requires much shorter simulation time,can be used to study their folding pathway and folding nucleus.[15–17]

Besides MD simulation techniques,Brooks et al.[18]and Go et al.[19]developed the normal mode analysis (NMA)method and successfully applied it to the protein-related research. The basic idea of the NMA method is first optimizing the protein structure based on an all-atom force field to obtain the equilibrium configuration of the system,then in the vicinity of the equilibrium configuration, the complex interactions between protein atoms are simplified to be harmonic potentials by ignoring higher-order terms, and finally the motion of the protein is decomposed into the superposition of normal motion modes. The NMA method does not require a longtime dynamic simulation to obtain the conformational properties of the system,which greatly reduces the computational cost. However,its accuracy is limited by the utilized classical all-atom force field and the result will be biased if the energy optimization is insufficient. On top of the NMA method,Bahar et al.[20,21]proposed the Gaussian network model(GNM),which reduces each amino acid residue to be a bead, the interaction between residues is represented by springs, and all springs have the same strength. The vibration of the residue around the equilibrium position is regarded as an isotropic Gaussian motion.[19,21]The GNM method focuses on global motions determined by slow modes because of their dominant role in controlling the collective dynamics of the protein,consistent with the experimentally measured hydrogen–deuterium exchange(HX)protection factor.[22]In addition,the GNM can be used to identify the so-called kinetically hot residues resulting in the peaks in the high frequency modes,which are linked to protein folding nuclei.[23]

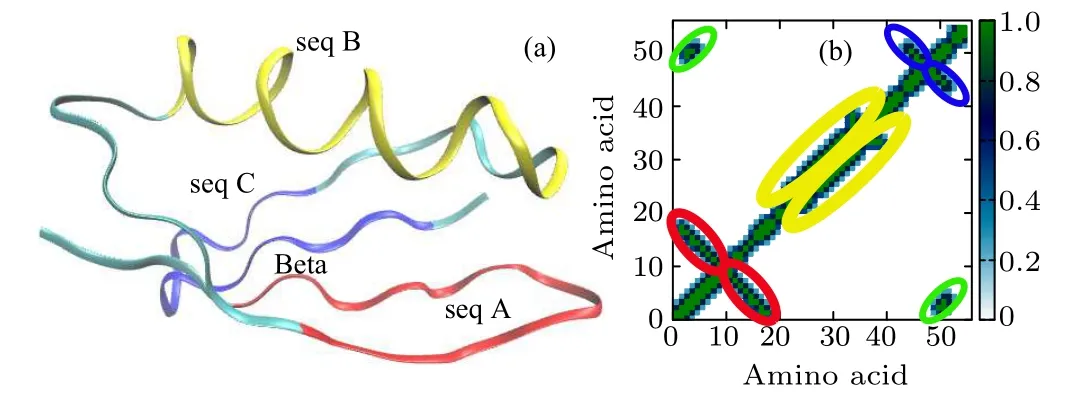
Fig.1. (a)Molecular structure of protein 2GB1 composed of four domains: seq A and seq C are hairpins,seq B is an α-helix,and Beta is a global β-sheet structure. (b) Contact map of the native structure. The red,orange,green,and blue ellipses highlight the regions corresponding to seq A,seq B,seq C,and Beta,respectively.

The small protein 2GB1(one of the GB1 family,PDB ID:2GB1)studied in this work has a thermodynamically very stable structure consisted of four domains: two β-hairpin structures denoted as seq A and seq C, respectively, an α-helix structure denoted as seq B, and a β-sheet structure denoted as Beta, as shown in Fig.1(a). There are plenty of hydrogen bonds in each domain, and hydrophobic amino acid residues are buried inside both the α-helix and the β-sheet domain to form a hydrophobic core. The contact map is used to clearly describe each secondary structure in its native state. Two Cαatoms are identified as “connected” if their distance is less than 7.0 ?A.In Fig.1(b),different domains in the contact map circled by red, orange, green, and blue ellipses correspond to seq A, seq B, seq C, and Beta sheet, respectively. The GNM method is used to identify the folding nucleus and pathway of 2GB1, and compared with the results of high-temperature unfolding MD.Both GNM and high-temperature MD indicate that the folding/unfolding of the protein is a two-state process,and the folding nucleus is located in the β-sheet region.

2. Methods

2.1. Gaussian network model

The GNM can be used to predict the protein folding nucleus, and the obtained results have a relatively high degree of agreement with experiments.[22]The GNM method identifies the kinetically hot residues serving as the protein folding nucleus by finding the peak of the fast motion mode.[23]The motion modes of a protein described by the GNM are entirely determined by the contact topology of the native configuration.Each amino acid residue is coarse-grained into a single bead whose position is set to be the coordinate of the Cαatom. It is assumed that a pair of beads are linked by an elastic spring if their distance is less than a certain cutoff rc.

The GNM mathematically describes the dynamics of the protein structure by the Kirchhoff matrix,whose elements are defined as

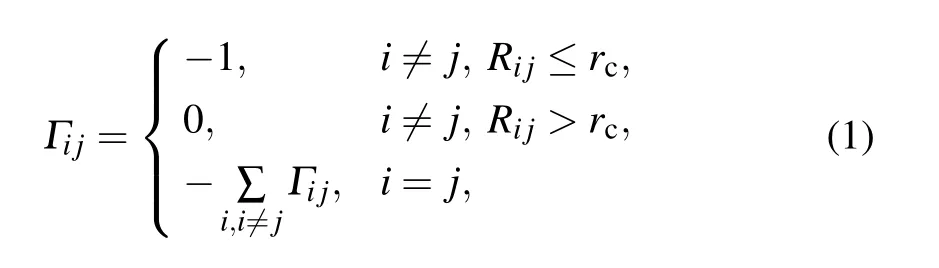
where Rijis the distance between the two points i and j, and rc=7 ?A in this work.The eigenvalues of the matrix reflect different motion modes. The low-frequency slow motion mode with a small eigenvalue corresponds to a large-scale collective motion, and quite often represents the functional motion of the system. By contrast,the high-frequency fast-motion mode with a large eigenvalue generally indicates the irregularity of the local structure of the system,quite often corresponding to the hot residues of the system.

2.2. Unfolding MD simulation

Due to the limitations of simulation time and computing resources, it is almost impossible to reproduce the folding process of proteins by conventional all-atom MD simulation, even for small proteins with less than 100 amino acid residues. Therefore, in this work, we investigate the folding nucleus and pathway of 2GB1 by performing the unfolding process at a high temperature. The native structure was used as the initial configuration for the unfolding MD simulation by using the GROMACS software package[24]with a simulation timestep of 2 fs. The OPLS-AA force field[25,26]was used to model the protein and the TIP4P[27]was used to model water molecules. The electrostatic interactions were treated with the particle-mesh-Ewald method,[28,29]and both the cutoff distances of the van der Waals (VDW) interaction and the real part of the electrostatic interaction were set to be 1.2 nm. The periodic boundary condition was applied to all three dimensions and the unfolding simulation was conducted in a constant NVT ensemble at the temperature T =480 K,which was kept a constant by the Nos′e–Hoover thermostat[30,31]with a coupling time of 0.2 ps.

2.3. Constrained MD

The complex potential energy surface of a protein has many energy barriers between the completely unfolded state and the native state. A conventional MD simulation cannot achieve the complete process of a fully stretched protein folding into its native structure.Therefore,we alternatively use the constrained MD to investigate the influence of the destruction of some local structures on the stability of the entire protein by constraining some parts of the protein in their native structures while the rest parts are free to become non-native. In the initial configuration,the whole protein retains its native structure except that a certain number of secondary structures deform,which is obtained by the following steps. First, each atom in its native position is fixed by a spring potential except those atoms in the domain to be destroyed. Then a regular MD simulation is performed in the NVT ensemble at 600 K for 10 ns to allow the unfixed domain lost its original secondary structure while the fixed domains kept their native structures. For instance, seq B is destroyed while other structures keep unchanged. The configuration with a certain secondary structure destroyed is then used as the initial configuration to further investigate the influence of different secondary structures on the stability of the entire protein. The system pressure is kept a constant of 1 atm by the Parrinello–Rahman barostat[32]with a coupling time of 0.5 ps.

3. Results and discussion

The GNM method was first used to determine the folding nucleus of protein 2GB1. Because the GNM method claims that the folding nucleus is composed of the amino acid residues with large fluctuations,the normalized mean-squared fluctuations of different Cαatoms of 2GB1 have been calculated and are shown in Fig.2(a),in which the initial five highfrequency normal modes were used. It can be seen that Y3,K4, L5, I6, A34, V39, T51, F52, and F53 atoms have large mean-squared fluctuations, indicating that they compose the folding nucleus. These atoms,all located in the Beta domain,are presented as color beads in the native structure shown in Fig.2(b)to clearly demonstrate their atomic positions.

In order to further understand the unfolding process of the protein and verify the conclusion drawn by the GNM method,a high-temperature MD simulation was then performed to investigate the unfolding process and the folding nucleus of 2GB1. The RMSDs with respect to the native structure and the connectivity of Cαatoms were calculated for the simulated configurations. As shown in Fig.3, the configurations generated by the unfolding simulation are projected on the space spanned by RMSD and contact number,whose plot is denoted as the RC map. The configurations are grouped into two parts in the RC map with the blank area in between, indicating a high energy barrier between the two parts, which manifests that the folding of 2GB1 is a two-state process,and there is a free energy barrier between the native state and the non-native state.

Fig.2. (a)Normalized mean-squared fluctuations of Cα atoms. (b)Color beads representing atoms with large mean-squared fluctuations in(a).

The average contact maps of the two states separated by the energy barrier are drawn in Figs. 4(a) and 4(b) to clearly show the conformational change after unfolding.It can be seen that all contact patterns remain the same except the Beta domain, in which the contact number is significantly reduced,indicating that the transformation from the native state to the non-native state occurs via the destruction of the Beta domain.The folding/unfolding pathway of protein 2GB1 can be deducted from the unfolding simulation trajectories as follows.The protein structure maintains its native conformation before the Beta domain is destroyed, after which the hydrophobic core formed by the Beta domain and seq B is also simultaneously destroyed, as shown in Fig.4(c). Seq B becomes unstable, begins to swing, and finally loses the spiral structure.After that,seq A and seq C lose the hairpin structure,and eventually the entire protein structure is destroyed and behaves randomly,as shown in Fig.4(d).

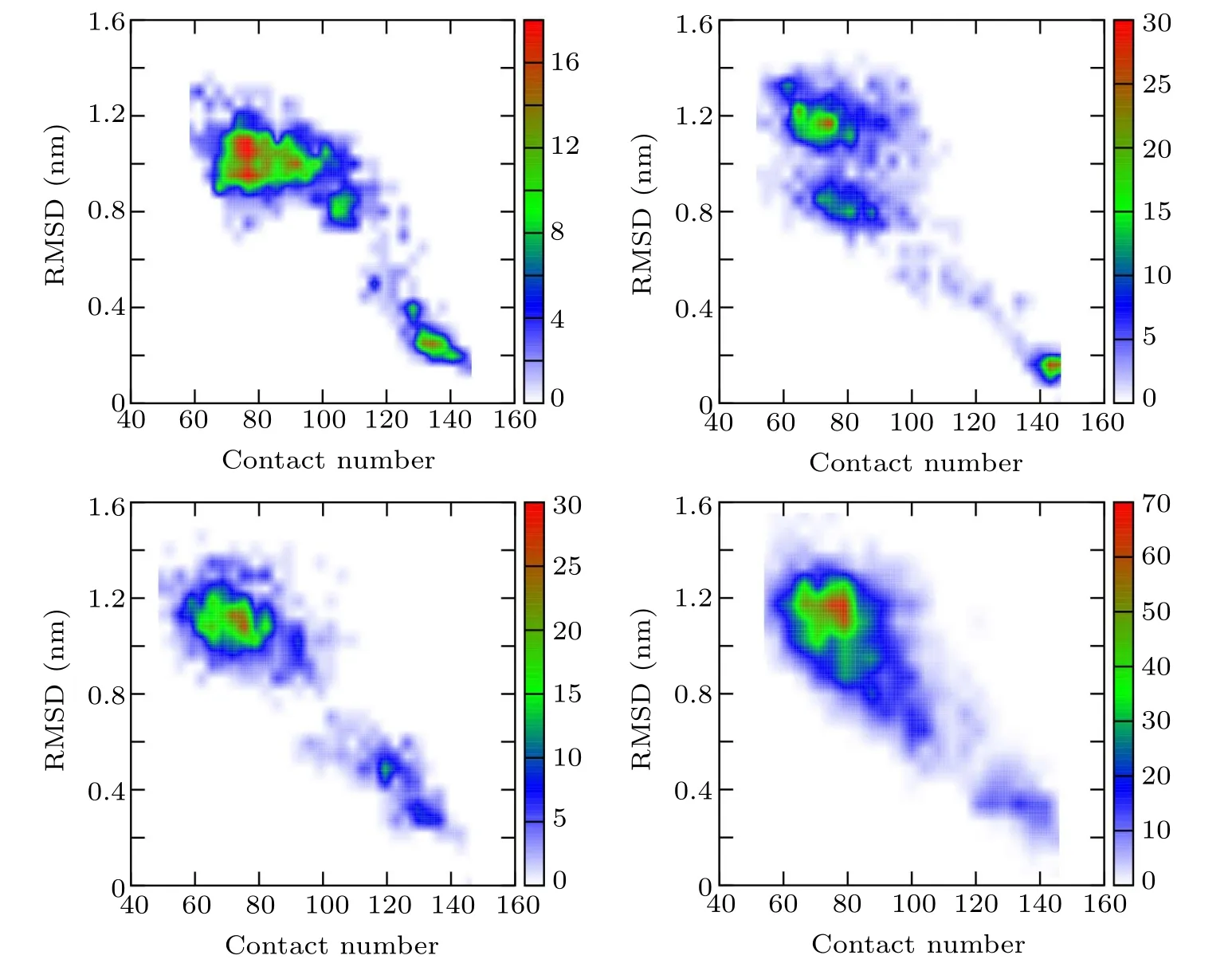
Fig.3. RC maps spanned by RMSD and contact number of four independent high-temperature unfolding simulations, indicating that the unfolding process of protein 2GB1 is a two-state process.

Fig.4. (a) and (b) Contact patterns before and after the energy barrier, respectively. (c) A random configuration illustrating that all parts keep unchanged except the folding nucleus,which is destroyed. (d)A random configuration illustrating that the hydrophobic core formed by seq B and Beta is destroyed.

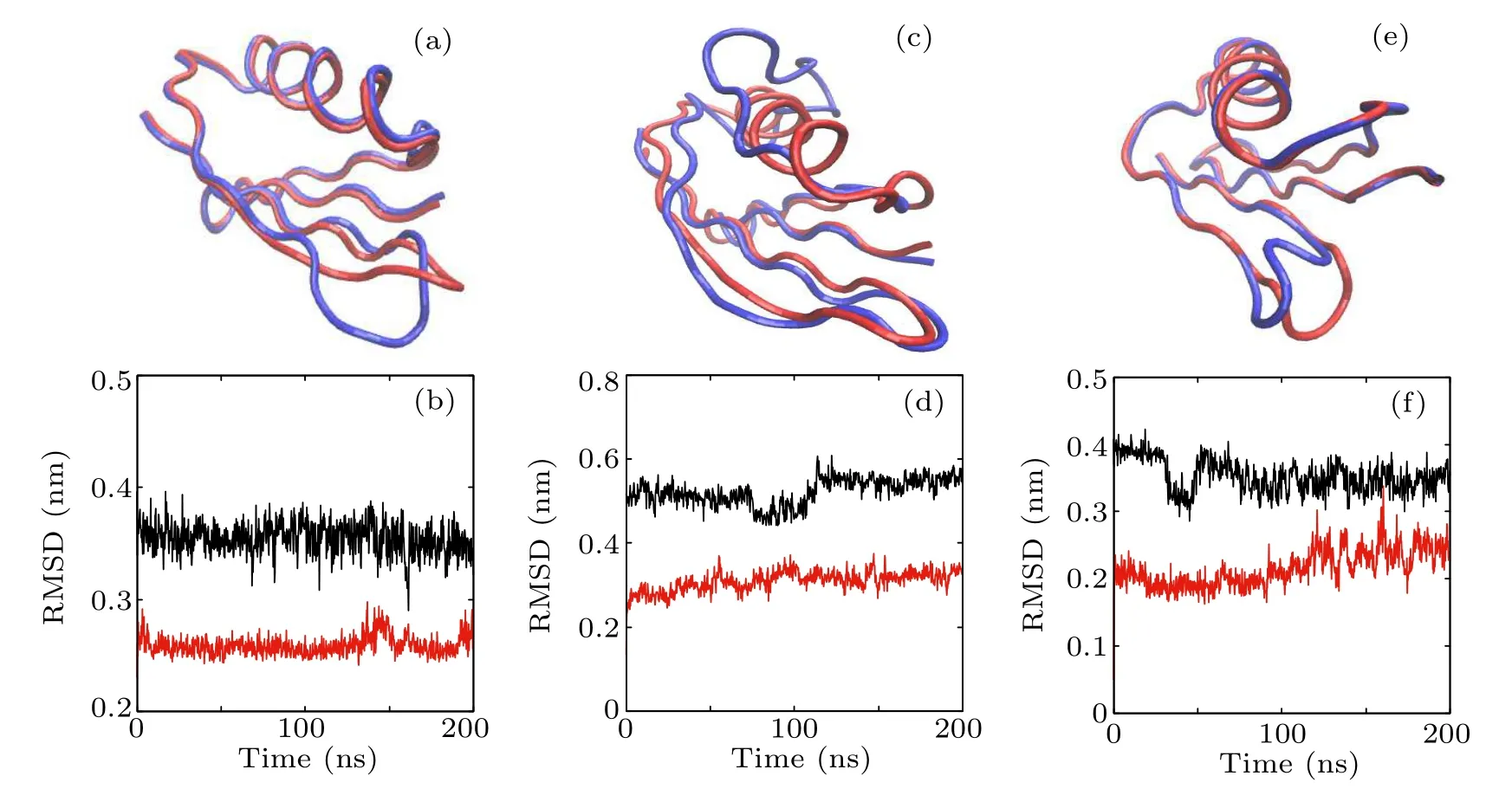
Fig.5. The initial structure with one secondary structure destroyed compared with the native state and the corresponding RMSD vs. simulation time of(a),(b)seq A;(c),(d)seq B;and(e),(f)seq C.The red and blue tubes in(a),(c),and(e)represent the backbones of the native and destroyed structures,respectively,and atoms in the destroyed domain are illustrated by ball and stick. The upper black lines in(b),(d),and(f)are the RMSD of the destroyed part with respect to the native structure and the lower red lines are the RMSD of all other parts of the protein with respect to the native structure.

Since Beta and seq B composing the hydrophobic core are destroyed simultaneously during the high temperature unfolding MD simulation,the constrained MD simulations were further performed to verify whether seq B is a part of the folding nucleus or not.We have destroyed one secondary structure at each time to serve as the initial configuration of a 200-ns MD simulation and the simulation results are shown in Fig.5.In Figs.5(a),5(c),and 5(e),the red tube represents the native structure and the blue tube represents the initial configuration that has one secondary structure destroyed. The black lines in Figs.5(b), 5(d), and 5(f)depict the RMSDs of the secondary structures after being destroyed with respect to the native secondary structure, and the red lines represent the RMSDs of the entire configurations except the destroyed structure with respect to its native structure. From these simulation results,it can be seen that,after the destruction of one secondary structure of seq A,seq B,or seq C,the rest of the protein structure remains almost unchanged. Figures 5(c) and 5(d) show that the destruction of seq B does not affect the structure of the Beta domain. During the 200-ns simulation time, the rest of the structure remains unchanged,indicating that seq B is not a part of the folding nucleus,and it is the hydrogen bonds in the Beta domain that stabilize the whole protein topology.

4. Conclusion

2GB1 is a small protein with a short sequence and good stability, which includes all typical secondary structures of a protein: two β-turn structures,one α-helix structure,and one β-sheet domain. It is a good model system for understanding some details of the protein folding dynamics. Because it is extremely difficult to study the folding nucleus and folding pathway using conventional MD simulation techniques even for such a small protein,accelerated simulation and advanced analysis methods are necessary. The GNM method indicates that the Beta domain of protein 2GB1 serves as the folding nucleus under the two-state folding theoretical framework, and multiple hydrogen bonds in the Beta domain stabilize the βsheet structure. The high-temperature unfolding MD simulation results are exhibited on the RC map spanned by RMSD and contact number as reaction coordinates, which confirms that the protein unfolding process is indeed a two-state process. Dynamically, the top of the barrier corresponds to the formation of the folding nucleus structure. By comparing the conformations at the two sides of the barrier, we have found that the biggest change in the structure occurs in the Beta region, which is the folding nucleus of the protein. During the unfolding process, the hydrogen bonds in the Beta region are first opened, and the seq B structure then starts to swing and loses its spiral structure. After the hydrogen bonds in the hairpin structures of seq A and seq C are opened,the entire protein structure finally collapses into a random coil.

This work utilizes multiple methods to find the folding nucleus and folding pathway of protein 2GB1,which are helpful for understanding the mechanism of protein folding. For similar small protein systems, it may be possible to quickly identify folding nucleus and pathway using the methods applied in this work as well as the RC map developed by us.

Acknowledgement

The computations of this work were conducted on the HPC cluster of ITP-CAS and the Tianhe-2 supercomputer.