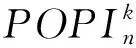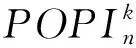半群的主因子的秩
呂 會 羅永貴
( 貴州師范大學數(shù)學科學學院,550025,貴陽 )
1 預備知識
設[n]={1,2,…,n-1,n}(n≥3)并賦予自然數(shù)的大小序.In表示[n]上的一一變換半群,SIn=InSn是[n]上的部分一一變換半群.設α∈SIn,若對任意的x,y∈dom(α),x≤y可推出xα≤yα,則稱α是保序的;若(1α,2α,…,nα)是一個圈,即最多存在一個自然數(shù)i, 使得iα>(i+1)α,則稱α是方向保序的.記OIn為InSn中所有保序變換之集,稱OIn為保序嚴格部分一一變換半群.記POPIn為InSn中所有方向保序變換之集,稱POPIn為方向保序嚴格部分一一變換半群.
設k是[n]上的一個固定點,令
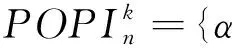
(1)
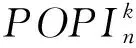
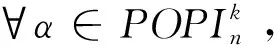
其中a1 αR◇β當且僅當ker(α)=ker(β), αL◇β當且僅當im(α)=im(β), αD◇β當且僅當|im(α)|=|im(β)|. (2) 易見,Pr關于運算· 是完全0 - 單半群. 定義2設 易知若θ1=σ1⊕δ1,θ2=σ2⊕δ2,則有θ1θ2=σ1σ2⊕δ1δ2. 定理1設n≥3,1≤r≤n-1,則 (3) 本文未定義的術語及符號參見文獻[7-9]. 為完成定理1的證明先給出如下兩個引理與一個推論. 證若(α,β),(α,αβ)∈D◇,則|im(α)|=|im(β)|=|im(αβ)|. 再由im(αβ)? im(β),ker(α)?ker(αβ)與[n]的有限性可知,im(αβ)=im(β),ker(α)=ker(αβ),即(α,αβ)∈R◇,(αβ,β)∈L◇. 推論1設n≥3,1≤r≤n-1,則 (4) 證分以下幾種情況討論: 設A1={p1 將αm換成 易知 是一個群. 對其余D-類也用類似方式進行構造,可得集合 當i 當i=j時,有α=αiαi+1…αm-1αmα1α2…αi-2αi-1. 當i>j時,有α=αiαi+1…αm-1αmα1α2α3…αj-2αj-1. 因此,結合推論1可得M是Pr的極小生成集, 且 綜上可知定理1得證.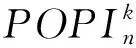
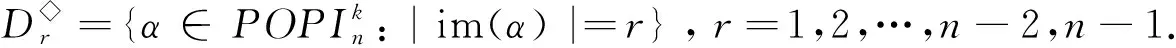
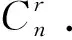
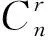
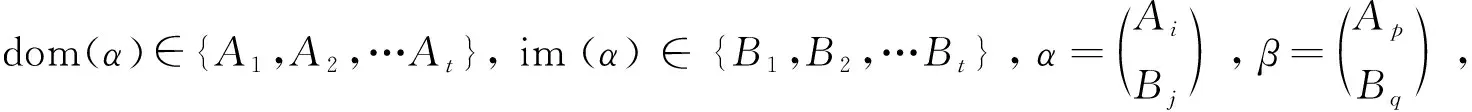
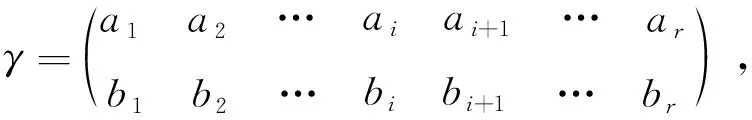
2 定理1的證明
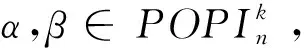
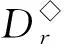
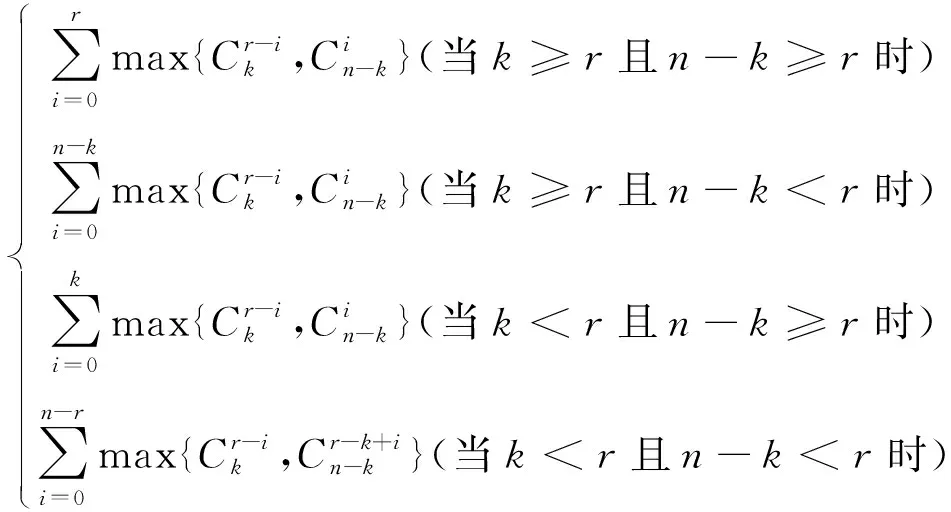
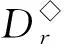
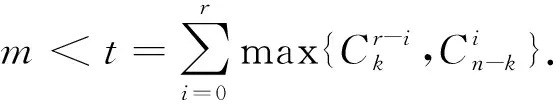
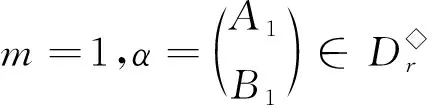
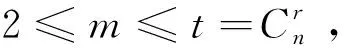
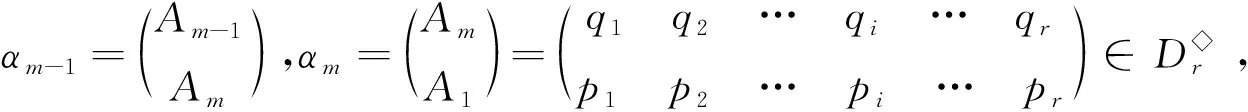
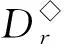
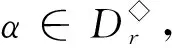
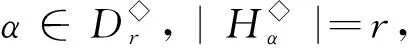
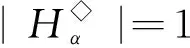
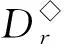
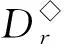
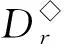
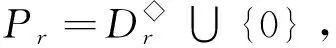
3 可進一步研究的問題