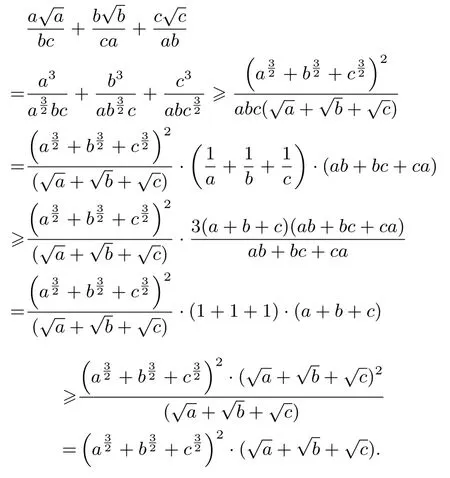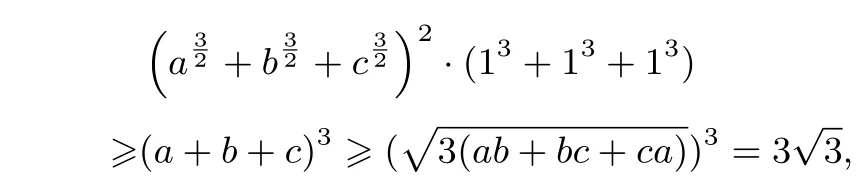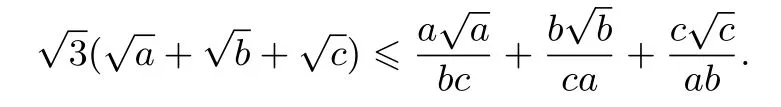河南省南陽師范學院軟件學院(473061) 李居之 孫文雪

河南省南陽理工學院軟件學院(473004) 陳 曦

設(shè)a,b,c為正實數(shù).由熟知的二元均值不等式a+b≥可以推導出一個常用的三元不等式(a+b+c)2≥3(ab+bc+ca).將其變形可得再將前面的三元不等式作代換a→ab,b→bc,c→ca,即得到另一個常用的三元不等式(ab+bc+ca)2≥3abc(a+b+c).將其變形可得結(jié)合前面就可以得到一個不等式鏈本文主要介紹利用這一左側(cè)不等式來解決一類三元分式不等式,下面舉例加以說明：

例1已知正數(shù)a,b,c滿足求證：ab+bc+ca≥3.

證明因為所以ab+bc+ca≥3.

類似地,還可以證明：

已知正數(shù)a,b,c滿足求證：a3+b3+c3+6abc≥9.

例2(2004年羅馬尼亞布加勒斯特數(shù)學競賽題)已知正數(shù)a,b,c滿足,ab+bc+ca=1,求證：

證明

類似地,還可以證明：

設(shè)a,b,c＞0,求證：

此即為1963年莫斯科數(shù)學競賽題,也即為著名的Nesbitt不等式.

例3 (《數(shù)學教學》問題869)a,b,c＞0,求證：

證明

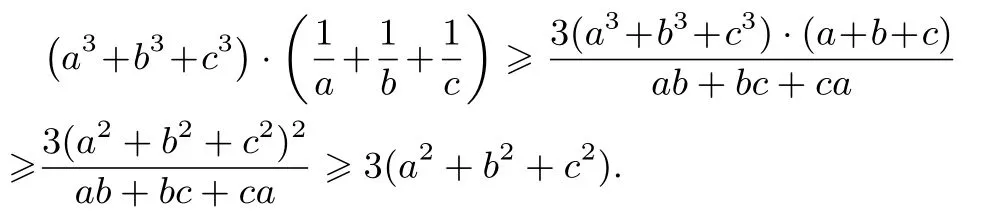
兩邊同時除以ab+bc+ca,即得

評注問題的原證明通過構(gòu)造函數(shù),利用函數(shù)的單調(diào)性證明了其技巧性較高且不易想到,而這一證法只用了三次局部放縮,便完成了證明,避免了原證明中較為復(fù)雜的技巧.

類似地,還可以證明《數(shù)學通報》問題2251：

設(shè)a,b,c＞0,求證：

例4設(shè)a,b,c＞0,求證：

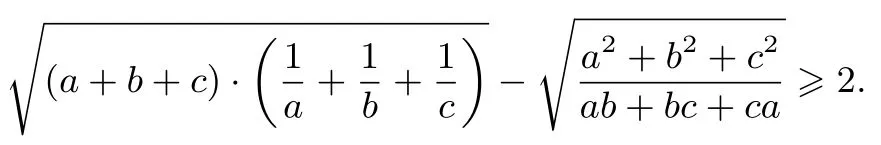
證明

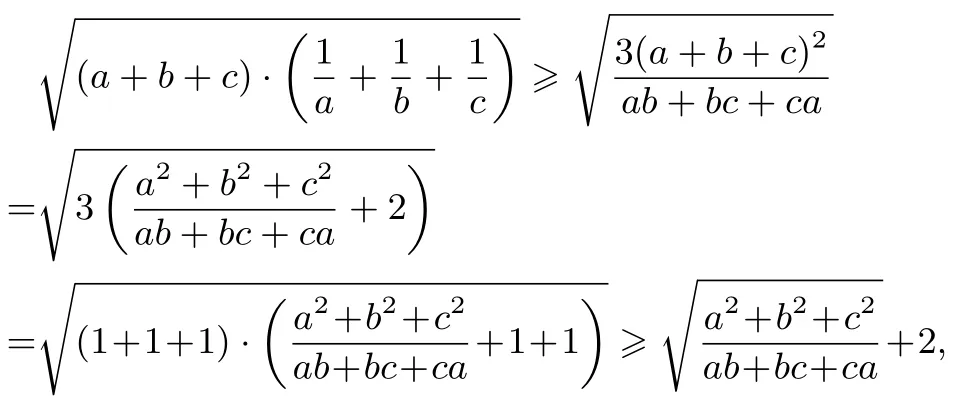
評注此題是安振平老師在新浪博客中提出的4853號問題,可能改編自《數(shù)學教學》問題1032：設(shè)a,b,c＞0,求證：

例5 已知正數(shù)a,b,c滿足ab+bc+ca=3,求證：

證明

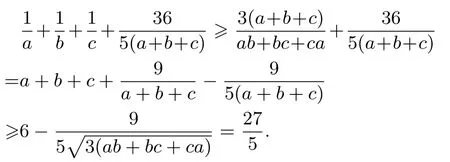
評注此問題改編自《數(shù)學通訊》問題304題.

類似地,還可以證明：已知正數(shù)a,b,c滿足a+b+c=3,求證：

例6 (2012年伊朗競賽題)已知正數(shù)a,b,c滿足ab+bc+ca=1,求證：

證明