熊琴

(廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣西 南寧 530004)

線性模型中廣義最小二乘參數(shù)估計誤差分布的穩(wěn)健性研究

熊琴

(廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣西 南寧 530004)

研究了線性模型中廣義最小二乘參數(shù)估計的誤差分布穩(wěn)健性問題.首先討論了在線性統(tǒng)計模型里,設(shè)計矩陣為列降秩矩陣時,模型中給出了誤差最大分布類,當(dāng)誤差向量的分布在此范圍內(nèi)變動時,LS估計和GLS估計在均方誤差矩陣準(zhǔn)則下是最優(yōu)估計.然后進一步探討廣義最小二乘估計GLSE關(guān)于誤差分布的穩(wěn)健性,求出誤差項所對應(yīng)的最大分布族,進而證明了在該區(qū)間波動情況下,誤差向量對應(yīng)的始終為一致最優(yōu)解.

線性模型;廣義均方誤差;穩(wěn)健性;廣義最小二乘估計;最佳線性無偏估計

1 引言

考慮線性模型Σ=y:

上式中y表示n×1階觀測向量,β表示p×1階未知參數(shù)向量的具體數(shù)值,X 表示n×p階矩陣情形,ε在上式中表示n×1隨機誤差向量,并且有rankX=r≤p.

在這里 φ(n)表示 n階正定陣集合,n階非負定陣集合用 φ(n)加以表示;A′表示 A的轉(zhuǎn)置所生成向量空間,而R(A)則表示A的列向量生成的向量;N(A)w=為R(A)的正交補空間;Z在這里代表一個符合X′Z=0條件下的n×(n?r)階列滿秩矩陣.A+表示A的Moore-penrose逆,誤差項ε的分布記為 P=h(ε),γ(u,V)表示期望u、協(xié)方差陣為δ2V 的分布族.其中

模型(1.1)中,當(dāng)前已經(jīng)有很多專家學(xué)者討論了函數(shù)c′β的LS估計誤差分布穩(wěn)健性問題以及GLS估計誤差分布穩(wěn)健性問題[1-2].目前已經(jīng)很多研究,在X 符合列滿秩定義的情況下,文獻[3-4]重點討論了β最小二乘估計在實際應(yīng)用中所具有積極意義,并對Gauss-Markov定理加以發(fā)展[5-7],從誤差分布最大類角度對其進行創(chuàng)新.

隨后,研究了當(dāng)rank(X)=r≤p時,在均方誤差矩陣準(zhǔn)則下Xβ的LS估計

定義 1.1給定Xβ的估計類χ及誤差項ε的一類分布γ(u,V),若δ?∈χ,并且

對所有 δ?∈ χ 及 P ∈ γ(u,V)都成立,則稱 Xβ 的估計 δ?是 [χ,γ(u,V)]最優(yōu).其中(δ,Xβ)為Xβ在γ上估計的廣義均方誤差數(shù)值,即:

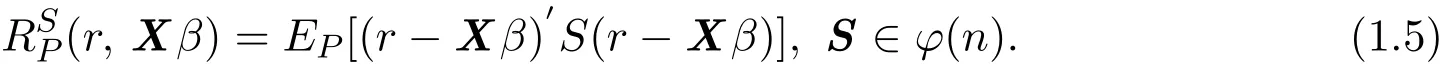
2 廣義最小二乘估計的穩(wěn)健性

本文中,對所構(gòu)建模型 (1.1),在廣義均方誤差準(zhǔn)則下研究函數(shù) Xβ的廣義最小二乘估計X(Σ)=X(X′Σ?1X)′X′Σ?1y的優(yōu)良性.

給定的估計類:

當(dāng) P=h(ε)∈γ(0,Σ)時,χ為可估函數(shù) Xβ的無偏估計類.在 P=h(ε)∈γ(u,Σ)條件滿足情況下,可估函數(shù)Xβ的更廣泛估計類這里我們用χ表示,其中涵蓋有偏估計和無偏估計兩大部分的內(nèi)容.研究明確了誤差項ε所對應(yīng)的最大分布族γ(Σ),從而保證了在γ(Σ)區(qū)間波動情況下,ε對應(yīng)的X(Σ)始終為[χ,γ(Σ)]最優(yōu).

引理 2.1設(shè)X 為n×p階矩陣,Z滿足X′Z=0且具有最大秩的矩陣,Σ∈φ(n),則有

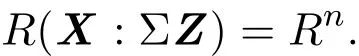
證明設(shè)任意 t∈R(X)∩R(ΣZ),存在 t1,t2,使得 t=Xt1= ΣZt2,利用 Z′X=0,Xt1=ΣZt2兩邊同時左乘Z′,得

由t的任意性,即得所要結(jié)論.

引理 2.3設(shè) Eε=u,Cov(ε)=V,A 為 n 階方陣,則有 E(ε′Aε)=u′Au+tr(AV).

3 主要結(jié)果

定理3.1若有P=h(ε)∈γ(u,V),那么常數(shù)Σ∈φ(n),X(Σ)對[χ,γ(Σ)]最優(yōu),其充分必要條件應(yīng)有:

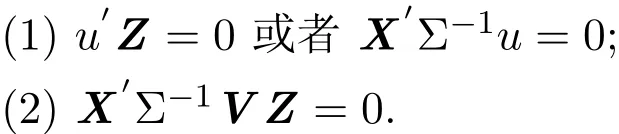
證明充分性.對任意P=h(ε)∈γ(u,V),當(dāng)條件(1),(2)成立時,有Gu=0或Hu=0且 HVG′,其中

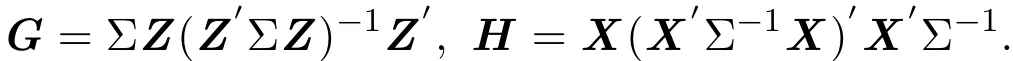
對任意 Ay∈χ,有AX=X,利用引理2.2,得

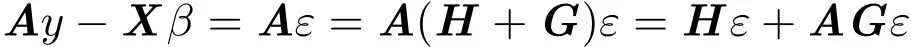
于是δ=Ay的廣義均方誤差:

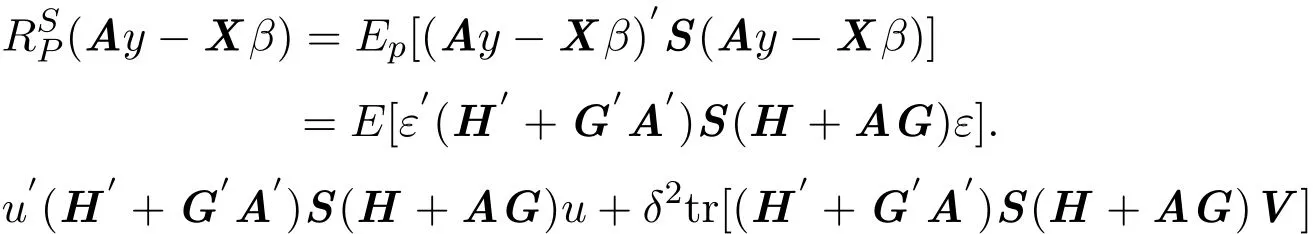
由

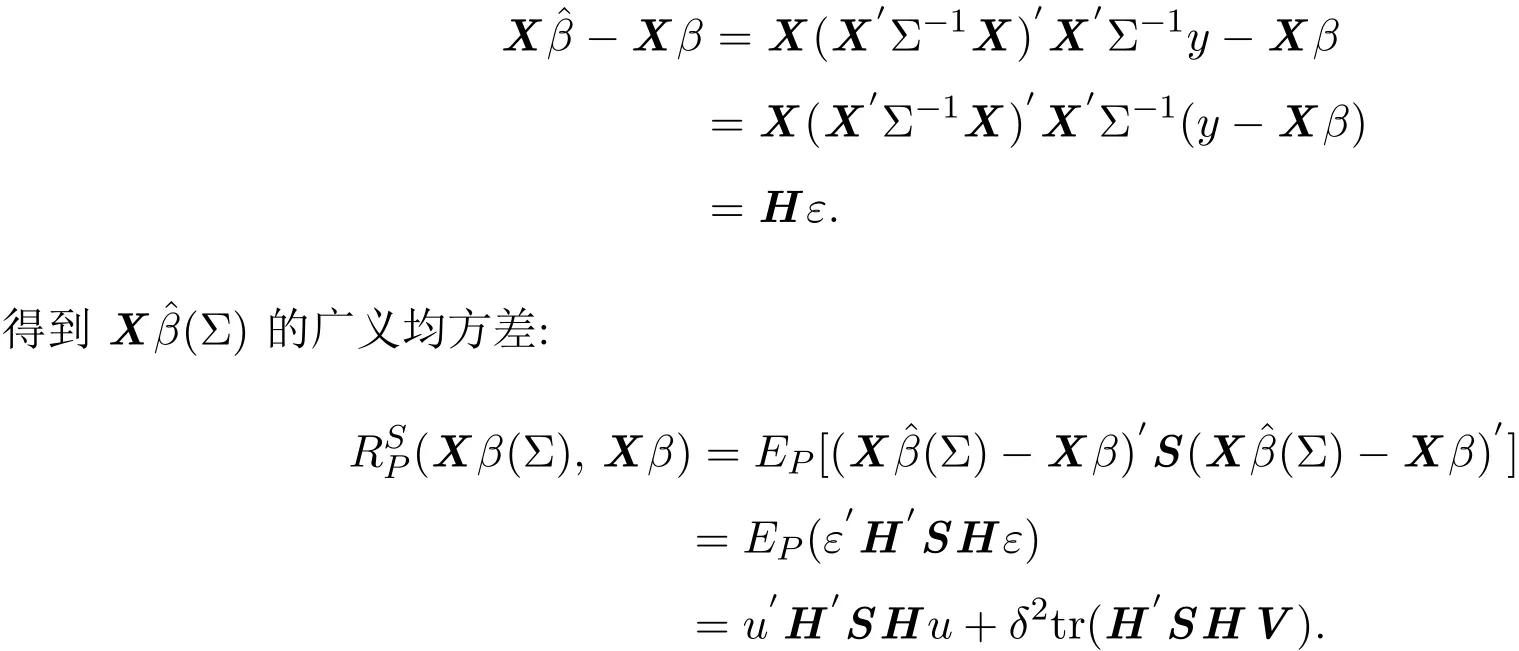
從而

任意的δ2>0等價于

(3.2)式成立,當(dāng)且僅當(dāng)任意的a,U 有

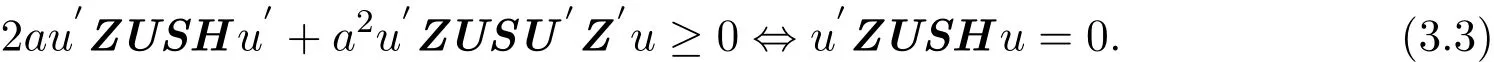
取 U=Z′uu′H′S?1,代入 (3.3)式,得:

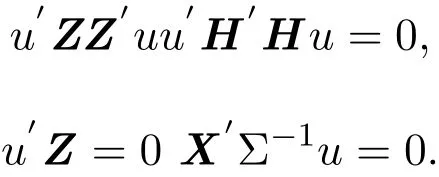
定理 3.2給定估計類χ,令

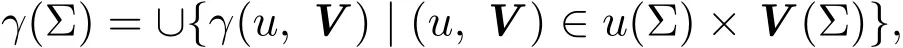
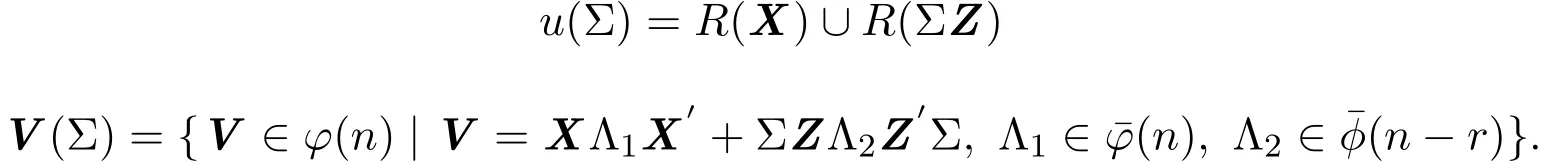
證明給定估計類χ,設(shè)X(Σ)是[χ,γ(Σ)]最優(yōu),則由定理3.1,有

而 u′Z=0等價于 u∈R(X),X′Σ?1u等價于 u∈R(ΣZ),從而

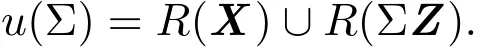
因 V ∈φ(n),則存在 n階可逆矩陣Q,使得V=QQ′,不妨設(shè)Q=(X:ΣZ)M,記

其中U1為p×n階矩陣,U2為(n?r)×n階矩陣,則

注意到 X′Z=0,有

則γ(I)是使得Xβ的最小二乘估計

為χ,γ(I)最優(yōu)的誤差項ε的最大分布類,其中

參考文獻

[1]邱紅兵,羅季,孫旭.奇異線性模型下最小范數(shù)二次無偏估計關(guān)于誤差分布的穩(wěn)健性[J].華僑大學(xué)學(xué)報:自然版,2012,33(1):112-116.

[2]邱紅兵.Bayes線性無偏估計關(guān)于誤差協(xié)方差及先驗分布的穩(wěn)健性[J].廣東工業(yè)大學(xué)學(xué)報,2016,33(5):5-8.

[3]Werner H J,Yapar C.A BLUE decomposition in the general linear regression model[J].Linear Algebra&Its Applications,1995,237-238:395-404.

[4]Kariya T,Kurata H.A Maximal Extension of the Gauss–Markov Theorem and Its Nonlinear Versions[M]//Generalized Least Squares.New York:John Wiley,2004:37-55.

[5]Jansen B J,Mullen T.Sponsored search:an overview of the concept,history,and technology[J].International Journal of Electronic Business,2008,6(2):114-131.

[6]邱紅兵,羅季.Gauss-Markov估計關(guān)于誤差分布的穩(wěn)健性[J].應(yīng)用概率統(tǒng)計,2010,26(6):615-622.

[7]胡桂開,彭萍.平衡損失下一般Gauss-Markov模型中回歸系數(shù)的最優(yōu)估計[J].應(yīng)用概率統(tǒng)計,2015,31(2):113-124.

[8]朱萬闖,林俊岐.基于格點搜索的隨機效應(yīng)的GLS估計[J].統(tǒng)計與信息論壇,2011,26(5):21-25.

[9]王松桂.線性模型的理論及其應(yīng)用[M].合肥:安徽教育出版社,1987.

On robustness of GLSE in terms of error distributions in linear model

Xiong Qin
(Guangxi University,Academy of Mathematics and Information Sciences,Nanning 530004,China)

In this paper,we study the problem of robustness error distribution of generalized least squares estimation in linear model.First of all,we discuss LS estimation and GLS estimation in the mean square error matrix criterion is the optimal estimation.When the designed matrix is for the column rank matrix,the model gives the maximum error distribution,and the error vector distribution changes in the range.Then we conclude robustness of generalized estimation in term of error distribution in linear model.Calculate the error item corresponding to the maximum distribution,which proves that in the interval fl uctuations,the error vector corresponding to the optimal solution is always consistent.

linear model,the generalized mean square error,robustness,generalized linear estimation,the best linear unbiased estimation

O212.1

A

1008-5513(2017)03-0307-07

10.3969/j.issn.1008-5513.2017.03.0010

2017-03-27.

國家自然科學(xué)基金(71462002);廣西自然科學(xué)基金(2013GXNSFAA019340).

熊琴(1982-),碩士生,研究方向:統(tǒng)計學(xué).

2010 MSC:05A17