涉及極點(diǎn)重級(jí)與分擔(dān)值的亞純函數(shù)正規(guī)定則
林瓊,葉亞盛,俞偉鵬
(上海理工大學(xué)理學(xué)院,上海 200093)
涉及極點(diǎn)重級(jí)與分擔(dān)值的亞純函數(shù)正規(guī)定則
林瓊,葉亞盛,俞偉鵬
(上海理工大學(xué)理學(xué)院,上海 200093)
運(yùn)用分擔(dān)值的思想證明了涉及極點(diǎn)重?cái)?shù)的亞純函數(shù)族的正規(guī)定則,所得結(jié)論推廣了相關(guān)文獻(xiàn)的主要結(jié)果.
極點(diǎn)重?cái)?shù);分擔(dān)值;正規(guī)族
1 引言
文獻(xiàn)[1]證明了如下著名的定理.
定理 A設(shè) f是復(fù)平面C上的亞純函數(shù),n(≥5)是正整數(shù),a(≠0),b是兩個(gè)有窮復(fù)數(shù).如果 f′+afn≠b,則 f 恒為常數(shù).
文獻(xiàn)[2]提出了相應(yīng)的正規(guī)定則,被許多學(xué)者相繼研究,得到如下結(jié)論,見文獻(xiàn)[3-8].
定理 B設(shè)F是區(qū)域D內(nèi)的一族亞純(全純)函數(shù),n,k是正整數(shù),a(≠0),b是兩個(gè)有窮復(fù)數(shù),如果 n≥k+3(n≥2),并且 ?f∈F,有 f(k)+afn≠b,則 F 在 D 內(nèi)正規(guī).
文獻(xiàn)[9]利用分擔(dān)值的思想證明了如果函數(shù)族中的任意一個(gè)函數(shù)和它的一階導(dǎo)數(shù)分擔(dān)三個(gè)有窮復(fù)數(shù),則該函數(shù)族在區(qū)域D內(nèi)是正規(guī)的.文獻(xiàn)[10]在定理B的基礎(chǔ)上考慮極點(diǎn)重?cái)?shù),證明了如下結(jié)論.
定理 C設(shè)k是正整數(shù),a(≠0),b是兩個(gè)有窮復(fù)數(shù),F是區(qū)域D內(nèi)的一族亞純函數(shù),族中每個(gè)函數(shù)的極點(diǎn)重?cái)?shù)至少為k+2.如果?f∈F,有f(k)+af3≠b,則F 在 D 內(nèi)正規(guī).
2012年文獻(xiàn)[11]用分擔(dān)值的思想推廣了定理B.
定理 D設(shè)n,k(n≥k+3)是兩個(gè)正整數(shù),a(≠0),b是兩個(gè)有窮復(fù)數(shù),F是區(qū)域D 內(nèi)的一族亞純函數(shù),族中每個(gè)函數(shù)的零點(diǎn)重?cái)?shù)至少為 k.如果?f,g∈F,有

在 D 內(nèi)分擔(dān) b,則F在D內(nèi)正規(guī).
本文將定理C與定理D推廣到了更一般的情形
定理 1.1設(shè) n(≥ 3),k是正整數(shù),a(≠0),b是有窮復(fù)數(shù),F 是區(qū)域 D 內(nèi)的一族亞純函數(shù),族中每個(gè)函數(shù)的零點(diǎn)重?cái)?shù)至少為 k,極點(diǎn)重?cái)?shù)至少為 k+1.如果 ?f,h∈F,有L(f)+afn與L(h)+ahn在D內(nèi)分擔(dān)b,其中

則F在區(qū)域D內(nèi)正規(guī).
例 1.1設(shè)是k≥2正整數(shù),

則對于F中任意兩個(gè)函數(shù)f,h,f(k)+afn與h(k)+ahn在D內(nèi)分擔(dān)0,但是F在D內(nèi)不正規(guī).
這說明定理1.1中的條件”族中每個(gè)函數(shù)的零點(diǎn)重?cái)?shù)至少為k”是必要的.
例1.2設(shè)

即 f′+af3與 h′+ah3在D 內(nèi)分擔(dān)0,但是F 在D 內(nèi)不正規(guī).
這說明定理1中的條件”族中每個(gè)函數(shù)的極點(diǎn)重?cái)?shù)至少為k+1”是必要的.
2 主要引理
為了完成定理1.1的證明,需要以下引理
引理 2.1[12-13]設(shè)F是單位圓盤△上的一族亞純函數(shù),且族中任意函數(shù)的所有零點(diǎn)重級(jí)均至少為p,所有極點(diǎn)重級(jí)均至少為q.設(shè)α是一個(gè)滿足?p<α (a)點(diǎn)列zn∈△,zn→z0; (b)函數(shù)列fn∈F; (c)數(shù)列 ρn→0+, 引理 2.2[14]設(shè)f是復(fù)平面C上的超越亞純函數(shù),n是非負(fù)整數(shù).如果fnP(f)=Q(f),且 deg Q≤n,其中 P,Q是 f 的微分多項(xiàng)式,它們的系數(shù) a(z)滿足 m(r,a)=S(r,f),則m(r,P(f))=S(r,f). 引理 2.3[15]設(shè)f是復(fù)平面C上的超越亞純函數(shù),滿足m(r,f)=S(r,f).若 其中A0(z),A1(z),A2(z)為f的小函數(shù). 引理 2.4設(shè) n(≥3),k是正整數(shù),a是非零常數(shù),f是復(fù)平面 C上的亞純函數(shù),如果 f(k)+afn≠0,且f的極點(diǎn)重級(jí)至少為k+1,則f退化為常數(shù). 由引理2.2知,m(r,H)=S(r,f). 由 f的極點(diǎn)重級(jí) p≥k+1,得 2p≥p+k+1,再根據(jù) (1)式中 f2的極點(diǎn)重級(jí)為 2p,φf(k)?f(k+1)的極點(diǎn)重級(jí)為p+k+1,可知f的極點(diǎn)不可能是H 的極點(diǎn).因此H 的極點(diǎn)只能由g的零點(diǎn)產(chǎn)生,故N(r,H)=N(r,1/g)=0,于是就有T(r,H)=S(r,f). 將 (3),(4),(5)式代入(1)式,則有 比較左右兩邊,從而有 其中 Pi(φ),Qi(φ)是 φ 的 i次多項(xiàng)式,其系數(shù) a(z)是 H,A1,A2的微分多項(xiàng)式,因而a(z)是f的小函數(shù). 下面將f(k)及f(k+1)代入(1)式并整理,得 則 fh1=h2,易見 f的 k+1級(jí)極點(diǎn)不可能是h1的極點(diǎn),由(2)式知,N(r,h1)=S(r,f),再由引理2.2知m(r,h1)=S(r,f),所以T(r,h1)=S(r,f),即h1是f的小函數(shù). 現(xiàn)在分兩種情形討論. 情形 1h1≡0,則 h2≡0,所以 H ≡0,即有兩邊積分得f3=c(f(k)+f3),即cf(k)≡(1?c)f3. 若 c=1,則 f(k)≡0,f是次數(shù)至多為 k?1的多項(xiàng)式,這與條件 f(k)+af3≠0矛盾;若 c≠1,由于 f的極點(diǎn)重?cái)?shù) p≥k+1,則 p+k=3p,即 k=2p≥2k+2,即 k+2≤0,矛盾. 情形 2h1?≡ 0,則于是有 于是就有T(r,f)=S(r,f),這對于非常數(shù)的f是不可能的,因此f是常數(shù). 引理2.5[16-17]設(shè)n是正整數(shù),b是非零常數(shù),f是復(fù)平面C上的亞純函數(shù),如果fnf′≠b,那么f 是常數(shù);進(jìn)一步,如果f是超越的,那么fnf′取每個(gè)非零有限值無窮多次. 引理 2.6設(shè)n(≥3),k是正整數(shù),a(≠0),b是兩個(gè)有窮復(fù)數(shù),F是區(qū)域D 內(nèi)的一族亞純函數(shù),族中每個(gè)函數(shù)的極點(diǎn)重?cái)?shù)至少為k+1.如果?f∈F,有L(f)+afn≠b,則F 在區(qū)域D 內(nèi)正規(guī). 證明過程完全類似于參考文獻(xiàn)[8]. 引理 2.7設(shè)(n≥3),k是正整數(shù),a是非零有窮復(fù)數(shù),f是復(fù)平面C上的非常數(shù)亞純函數(shù),若f的所有零點(diǎn)重級(jí)至少為k,極點(diǎn)重級(jí)至少為k+1,則f(k)(z)+afn(z)至少有兩個(gè)判別零點(diǎn). 證明假設(shè)f(k)(z)+afn(z)只有一個(gè)零點(diǎn),以下分兩種情形討論. 情形 1當(dāng)k≥2時(shí),令 由 f的零點(diǎn)重級(jí)至少為 k知 f(k)?≡0,所以 ψ(z)?≡0.由 (8)式 ,得 由f的極點(diǎn)重級(jí)p≥k+1知,p+k=np,k=(n?1)p≥(n?1)(k+1),這是不可能的.所以f是整函數(shù).于是 情形 2k=1時(shí),令于是φ的零點(diǎn)重級(jí)≥2. 因?yàn)?/p> 只有一個(gè)零點(diǎn),記為 ξ0,于是ξ0是φ的重級(jí)極點(diǎn)或者是φn?2φ′?a的零點(diǎn). 若 φ 是非常數(shù)多項(xiàng)式,則 φn?2φ′?a=B(z? ξ0)l,其中 B 是非零常數(shù),l是正整數(shù),且l≥3. 由于 ψ 的零點(diǎn)重級(jí) ≥ 4,ψ′的唯一零點(diǎn) ξ0也是 ψ′的零點(diǎn),故 ψ′(ξ0)=0,于是 a=0,這與a≠0矛盾.因此φ和ψ只能是非多項(xiàng)式的有理函數(shù).設(shè) 其中 其中B是非常數(shù),因此 其中h3也是多項(xiàng)式. 從 (15)-(17)式,可知 類似地,由(19),(20)式得 因此 m+t?i=3t,m=2t+i≠2t,從 (15)式可知,deg(h1)=s+t?1,則 deg(p1)=m+t?1,于是m+t?1=3t,即2t+1=m≤2t,矛盾. 證明不失一般性,設(shè)D=△={z:|z|≤1},任取z0∈D,下面證明F在z0處正規(guī).?f∈F分兩種情況討論. 情形 1L(f(z0))+afn(z0) ≠b 則 ? δ>0,使得 ?z∈Dδ={z:|z?z0|< δ}有 L(f(z))+afn(z)≠b.于是 ?h∈F,在 Dδ內(nèi)有L(h(z))+ahn(z)≠b,則由引理2.6知,F 在Dδ內(nèi)正規(guī),于是 F 在 z0處正規(guī). 情形 2L(f(z0))+afn(z0)=b.再分兩種情形討論. 情形 2.1L(f)+afn= b. 下證F在z0處正規(guī). 假設(shè)F 在z0處不正規(guī).由引理2.1知,?{fj}?F,zj∈△,zj→z0,ρj→0+,使得 在復(fù)平面C 上按球距內(nèi)閉一致收斂于g(ξ),其中g(shù)(ξ)是復(fù)平面C 上的非常數(shù)亞純函數(shù).因此 gj(ξ)在 C 上去掉 g的極點(diǎn)后的區(qū)域內(nèi)內(nèi)閉一致收斂于 g(ξ).顯然g(ξ)的所有極點(diǎn)重級(jí)也至少是k+1,所以 在復(fù)平面C 去掉g的極點(diǎn)后的區(qū)域內(nèi)內(nèi)閉一致收斂于akg(k)(ξ)+agn(ξ). 若 akg(k)(ξ)+agn(ξ)≡ 0,設(shè) ξ0是 g(ξ)的重級(jí)為 p的極點(diǎn),p≥ k+1,則有 p+k=np,即k=(n?1)p.由p≥k+1知,k≥(n?1)(k+1),這是不可能的.所以g是整函數(shù).于是有 即T(r,g)=S(r,g),這與g是非常數(shù)亞純函數(shù)矛盾. 由條件?f,h∈F,L(f)+afn與L(h)+ahn在區(qū)域D內(nèi)分擔(dān)b,知對于任意的正整數(shù)m,有 情形 2.2L(f)+afn≡b. 證明過程完全類似于情形2.1中akg(k)(ξ)+agn(ξ)≡0的情況. 綜上所述,F在z0處正規(guī),由z0的任意性可知,F在D內(nèi)正規(guī). [1]Hayman W K.Picard values of meromorphic functions and their derivatives[J].Annals of Mathematics,1959,5(3):28-32. [2]Hayman W K.Research Problems in Function Theory[M].London:Athione Press,1967. [3]龐學(xué)誠.微分多項(xiàng)式的正規(guī)定則[J].科學(xué)通報(bào),1988,33:1690-1693. [4]Schwick W.Normality criteria for families of meromorphic functions[J].J.Analyse Mat.,1989,52:241-289. [5]Ye Y S,Pang X C.On the zeros of a di ff erential polynomial and normal families[J].J.Math.Anal.Appl.,1997,205(1):32-42. [6]Xu Y.Normal families of meromorphic functions[J].J.Math.Wuhan,2001,21:381-386. [7]雷春林,方明亮,楊德貴,等.關(guān)于Hayman問題與分擔(dān)值[J].數(shù)學(xué)物理學(xué)報(bào),2008(5):802-807. [8]葉亞盛.一個(gè)涉及極點(diǎn)重?cái)?shù)的亞純函數(shù)正規(guī)定則[J].上海理工大學(xué)學(xué)報(bào),2007(3):265-267. [9]Schwick W.Sharing values and normality[J].Archiv der Mathematics,1992,59(1):50-54. [10]陳懷惠,顧永興.Marty定則的改進(jìn)及其應(yīng)用[J].中國科學(xué):A輯,1993,23(2):123-129. [11]仇惠玲,劉丹,方明亮.涉及正規(guī)族與分擔(dān)值的Hayman問題[J].中國科學(xué):數(shù)學(xué),2012,42(6):603-610. [12]Pang X C,Zalcman L.Normal families and shared values[J].Bull London Math.Soc.,2000,32(3):325-331. [13]Zalcman L.Normal families:New perspectives[J].Bull Amer.Math.Soc.,1998,35:215-230. [14]Clunie J.On integral and meromorphic functions[J].J.London Math.Soc.,1962,37(1):17-27. [15]Steinmetz N.¨Uber die nullstellen von di ff erential polynomial[J].Math.Z.,1981,176(2):255-264. [16]Bergweiler W,Eremenko A.On the singularities of the inverse to a meromorphic function of fi nite order[J].Rev.Math.Iberoamericana.,1995,11(2):355-259. [17]陳懷惠,方明亮.關(guān)于fnf′的值分布[J].中國科學(xué):A輯,1995(7):38-39. Normal criterion of meromorphic functions with multiple poles and shared values Lin Qiong,Ye Yasheng,Yu Weipeng This paper considers normality criteria for a family of meromorphic functions concerning multiple poles by the thought of sharing value,our results generalize the theorems of related papers and references. multiple poles,shared values,normal family O174.52 A 1008-5513(2017)03-0286-12 10.3969/j.issn.1008-5513.2017.03.008 2017-03-22. 國家自然科學(xué)基金(11371139). 林瓊(1990-),碩士生,研究方向:基礎(chǔ)數(shù)學(xué). 2010 MSC:30D45







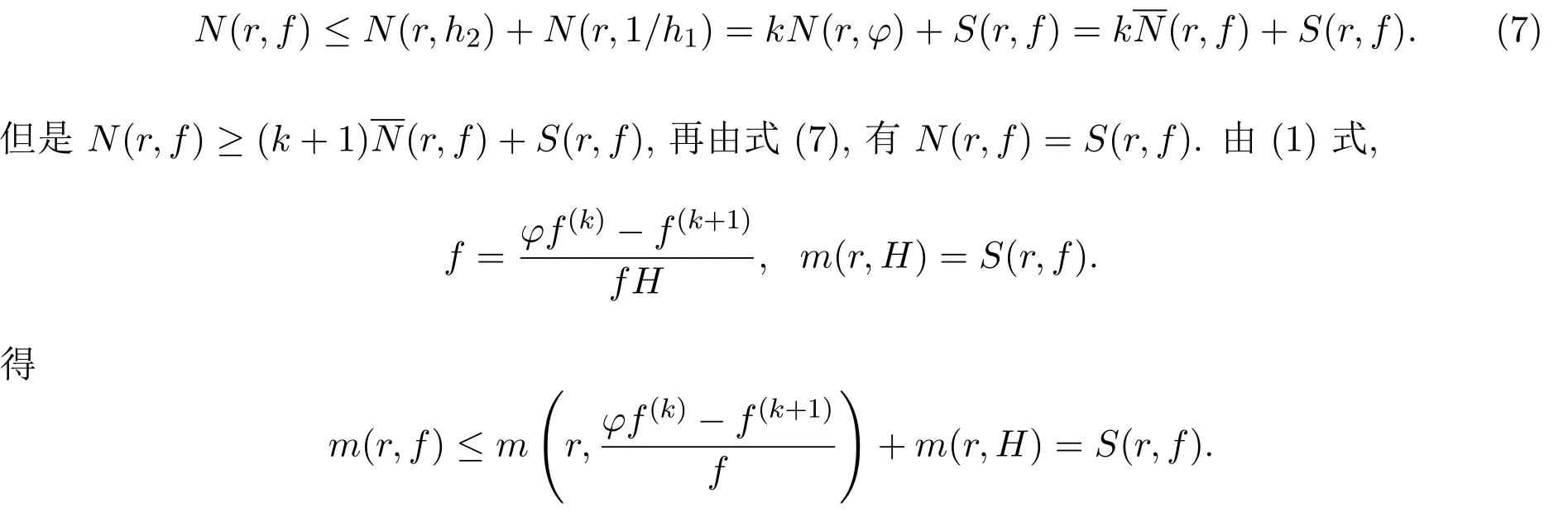



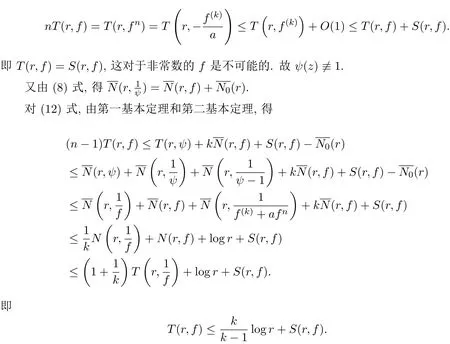





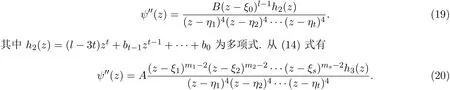


3 定理的證明


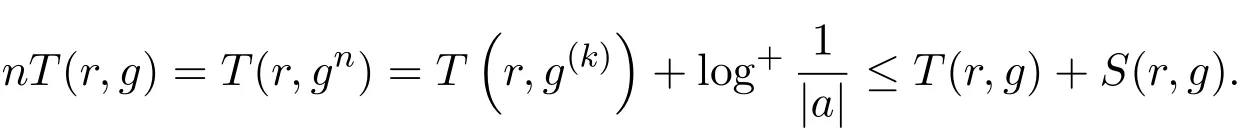


(College of Science,University of Shanghai for Science and Technology,Shanghai200093,China)

