泊松分布與負二項分布在模擬索賠次數(shù)中的應(yīng)用
王丙參,魏艷華,石春燕
(天水師范學院數(shù)學與統(tǒng)計學院,甘肅天水741001)
泊松分布與負二項分布在模擬索賠次數(shù)中的應(yīng)用
王丙參,魏艷華,石春燕
(天水師范學院數(shù)學與統(tǒng)計學院,甘肅天水741001)
為了在模擬索賠次數(shù)時更好的運用泊松分布與負二項分布,研究了二者的優(yōu)良特性及相互關(guān)系,最后結(jié)合Sas軟件進行實例分析,得到了負二項分布是伽瑪分布對泊松分布的混合分布且是賠頻率強度存在正傳染性的索賠分布,由于方差大于均值,因而更好的描述非同質(zhì)風險.
泊松分布;負二項分布;索賠次數(shù);估計值
在實際中,不會有大量數(shù)據(jù)可以確定理賠次數(shù)的分布,因此必須為理賠次數(shù)選擇一個合適的模型來擬和.泊松分布與負二項分布都能比較滿意地用來擬和風險集體的理賠次數(shù),還具有其它分布不能企及的優(yōu)良特性[1-4].鑒于此,本文研究了泊松分布與負二項分布的優(yōu)良特性及相互關(guān)系,以便在模擬索賠次數(shù)時更好的運用它們,并結(jié)合Sas軟件進行實例分析.
1 基本模型
為了描述稀有事件,只含有一個參數(shù)的泊松分布往往是第一選擇,當風險集體同質(zhì)時,理賠次數(shù)服從Poisson分布,均值等于方差[5].
負二項分布有兩個基本模型:
(1)若在伯努利試驗序列中,每次試驗成功的概率為p,則恰好出現(xiàn)n次成功所需試驗次數(shù)X服從
泊松分布X以全體自然數(shù)為一切可能值,其分布律為參數(shù)為(n,p)的第一類負二項分布,記為0 可見,在長度為h的時間區(qū)間內(nèi)發(fā)生k次索賠的概率服從參數(shù)為(αn,p(h))的第二類型負二項分布.幾乎所有的汽車保險人都采用了無賠款優(yōu)待系統(tǒng)(BM S),根據(jù)投保人以往年份的索賠情況調(diào)整其續(xù)期保費.通常的原則是,上一保險年度發(fā)生的索賠次數(shù)越多,次年的續(xù)期保費將越高,反之則否.保險公司調(diào)整投保人續(xù)期保費的主要目的之一就是為了公平投保人的保費負擔,使高風險的投保人繳納相對較高的保險費,并且有人設(shè)計出了最優(yōu)BM S,可以根據(jù)投保人的索賠經(jīng)驗對投保人的續(xù)期保費進行調(diào)整,但該模型假定單個投保人的索賠次數(shù)服從泊松分布,這意味著投保人以前是否發(fā)生過保險事故對今后是沒有影響的,但實際上投保人的索賠經(jīng)歷往往具有傳染性.由于負二項分布是一種正向傳染模型,在這種情況下單個投保人的索賠次數(shù)可能更加接近于服從負二項分布,因此風險理論中在擬合索賠次數(shù)時常用第二種類型的負二項分布.容易看出,負二項分布有一個很簡單的性質(zhì),方差大于均值.負二項分布的方差越大于其均值,表明投保集體存在的非同質(zhì)性越嚴重[5]. 利用表1數(shù)據(jù)擬合泊松分布與負二項分布: 表1 某車險的理賠數(shù)據(jù)[7] 模擬結(jié)果為表2: 表2 估計的發(fā)生賠案的保單數(shù)目 顯然數(shù)據(jù)的期望估計值0.101 080 636 42小于方差的估計值0.107 447 814 67,所以運用負二項分布進行估計更加精確,事實上模擬結(jié)果確實如此. [1]王丙參,魏艷華.保費收取次數(shù)為負二項隨機過程的風險模型[J].江西師范大學學報,2010,34(06):604-608 [2]王丙參,徐長偉,宋立新.概率分布中的遞推問題與Panjer遞推公式[J].河北北方學院學報:自然科學版,2010, 26(02):13-15 [3]吳建祥,楊海忠.同質(zhì)性保單索賠次數(shù)的一種分布類討論[J].統(tǒng)計與決策,2009,(18):154-156 [4]孟生旺.負二項分布的優(yōu)良特性及其在風險管理中的應(yīng)用[J].數(shù)理統(tǒng)計與管理,1998,17(02):9-12 [5]Klugman SA,Panjer HH著,吳嵐譯.損失模型從數(shù)據(jù)到?jīng)Q策[M].北京:人民郵電出版社,2009:350-370 [6]Biihlmann H.Mathematical Methods in Risk Theo ry[M].Berlin:Sp ringer-Verlag,1996:100-120 [7]楊靜平.非壽險精算學[M].北京:北京大學出版社,2006:75-91 [責任編輯:劉守義] Applications of Poisson Distribution and Negative Binom ial Distribution in Stochastic Simulation of Number of Claims WANGBing-can,WEIYan-hua,SHIChun-yan (School of Mathematics and Statistics,Tianshui No rmal University,Tianshui 741001,Gansu,China) This paper discusses the p roperties and relationship betw een the negative binomial distribution and Poisson distribution in o rder to use them in the stochastic sim ulation of num ber of claim s.Finally,it analyzes an examp le by using Sas software.Negative binomial distribution is a gamma mixture of Poisson distribution.When claim frequency in tensities has positive contagion,the claim num ber distribution is negative binomial distribution.Since the variance is bigger than themean,it is a better descrip tion of the non-homogeneous risk. Poisson distribution;negative binomial distribution;number of claim s;estimate O 211.3 A 1673-1492(2011)02-0013-04 來稿日期:2011-03-17 甘肅省自然科學研究基金計劃(096RJZE106);天水師范學院科研基金(TSA0931) 王丙參(1983-),男,河南南陽人,天水師范學院數(shù)學與統(tǒng)計學院講師,碩士.
2 第二類負二項分布與泊松分布的關(guān)系及性質(zhì)


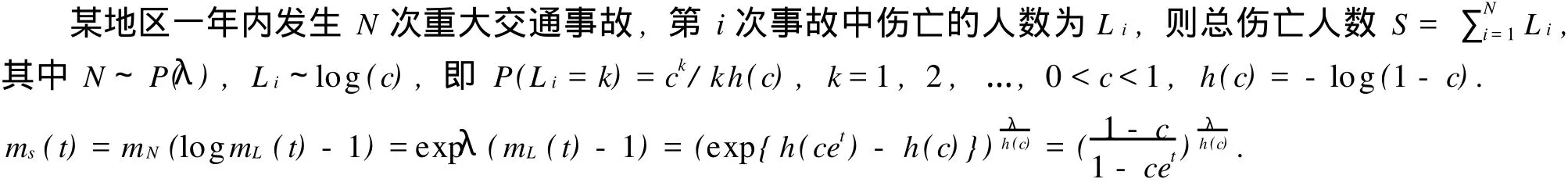
3 結(jié)合Sas軟件進行實例分析




