? 陜西省西安市第七十一中學(xué) 尚 萍

1 一個(gè)實(shí)例及解法

例1已知數(shù)列{an}滿(mǎn)足a1=1,a2=2,且an+1=2an+3an-1(n≥2,n∈N+)．求數(shù)列{an}的通項(xiàng)公式.

解法1：常規(guī)解法.

因?yàn)閍n+1=2an+3an-1(n≥2,n∈N+),所以an+1+an=3(an+an-1)(n≥2).

又因?yàn)閍2+a1=3,所以{an+1+an}是以3為首項(xiàng),3為公比的等比數(shù)列．

所以an+1+an=3×3n-1=3n,從而

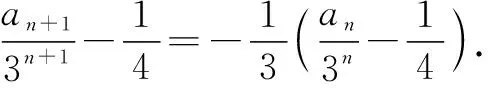
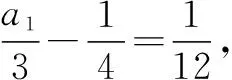
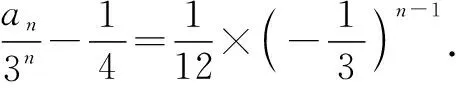
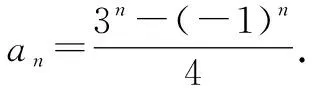
解法2：特征方程法.

設(shè)an+1-x1an=x2(an-x1an-1),與an+1=2an+3an-1比較系數(shù),得

由韋達(dá)定理可知,x1,x2是方程x2-2x-3=0的兩根-1和3.

取x1=-1,x2=3,有an+1+an=3(an+an-1).又因?yàn)閍2+a1=3,所以{an+1+an}是以3為首項(xiàng),3為公比的等比數(shù)列,所以an+1+an=3×3n-1=3n.

取x1=3,x2=-1,有an+1-3an=-(an-3an-1).又因?yàn)閍2-3a1=-1,所以{an+1-3an}是以-1為首項(xiàng),-1為公比的等比數(shù)列,則an+1-3an=(-1)×(-1)n-1=(-1)n.

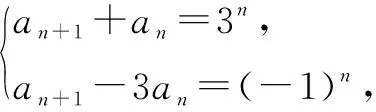
因此,設(shè)an=c1·(-1)n+c2·3n.

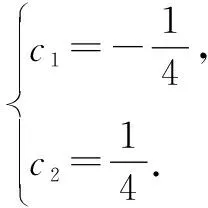
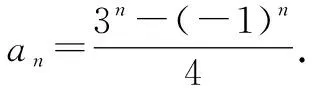
2 利用特征方程法解題的步驟

由例1解法2的解析可以看出,特征方程法是將相鄰兩項(xiàng)的線(xiàn)性組合構(gòu)造成等比數(shù)列[1],而對(duì)應(yīng)的系數(shù)剛好是題目中相鄰三項(xiàng)線(xiàn)性遞推關(guān)系數(shù)列的特征方程的根,通過(guò)解特征方程可以直接寫(xiě)出最終an的表達(dá)形式,再根據(jù)數(shù)列中的任意兩項(xiàng),求出線(xiàn)性組合的系數(shù),最終得到數(shù)列{an}的通項(xiàng)公式[2].因此可以將解題過(guò)程簡(jiǎn)化為以下三個(gè)步驟：

(1)寫(xiě)出特征方程并求出兩根x1,x2;

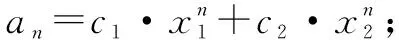
(3)將a1,a2的值代入求出系數(shù)c1,c2,進(jìn)而寫(xiě)出數(shù)列{an}的通項(xiàng)公式.

例2已知數(shù)列{an}滿(mǎn)足a1=a2=2,且an+1=3an+4an-1(n≥2,n∈N+)．求數(shù)列{an}的通項(xiàng)公式.

解析：特征方程法.

由題可知,數(shù)列的特征方程為x2-3x-4=0,解方程得x1=4,x2=-1.

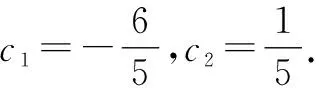
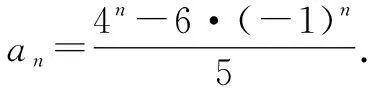
由例2的解析[3]可以看出,利用特征方程法解決此類(lèi)問(wèn)題具有簡(jiǎn)潔快速的明顯優(yōu)勢(shì),同時(shí)在解題過(guò)程中不容易出現(xiàn)錯(cuò)誤,非常適合高中階段的學(xué)生學(xué)習(xí)和理解.

3 特征方程法應(yīng)用中的問(wèn)題及對(duì)策

利用特征方程法求解這類(lèi)問(wèn)題,關(guān)鍵是構(gòu)造特征方程.對(duì)于形如an+2=aan+1+ban(a,b為常數(shù))的遞推數(shù)列,它的特征方程是x2=ax+b,即x2-ax-b=0.

另外,既然是二次方程就可能存在兩個(gè)相等的根和無(wú)實(shí)根的情形,下面對(duì)這兩種情形進(jìn)行探究.

例3已知數(shù)列{an}滿(mǎn)足a1=1,a2=2,且an+1=6an-9an-1(n≥2,n∈N+)．求數(shù)列{an}的通項(xiàng)公式.

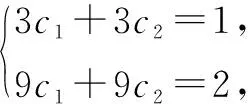
因此 ,例3無(wú)法用特征方程法快速求出通項(xiàng)公式.下面繼續(xù)用構(gòu)造等差數(shù)列的方法重新求解,探求新思路[2].

解析：常規(guī)解法.

因?yàn)閍n+1=6an-9an-1(n≥2,n∈N+),所以an+1-3an=3(an-3an-1)(n≥2).又因?yàn)閍2-3a1=-1,所以{an+1-3an}是首項(xiàng)為-1,公比為3的等比數(shù)列．

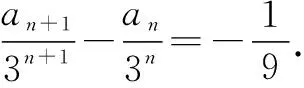
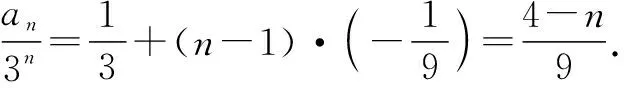
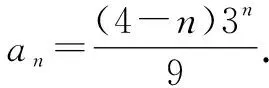
由例3可以看出,當(dāng)特征方程有兩個(gè)相等的根時(shí),無(wú)法用特征方程法求出數(shù)列的通項(xiàng)公式,此時(shí)需要構(gòu)造一個(gè)新的等差數(shù)列,求出這個(gè)等差數(shù)列的通項(xiàng)公式是An+B的形式,進(jìn)而求出數(shù)列{an}的通項(xiàng)公式an=(An+B)·xn.

例4已知數(shù)列{an}滿(mǎn)足a1=1,a2=2,且an+1=an-an-1(n≥2,n∈N+)．求a2 024.

解析：由題可知,數(shù)列的特征方程為x2-x+1=0,此方程無(wú)實(shí)數(shù)根.

由a1=1,a2=2,an+1=an-an-1分別計(jì)算可得

a3=1,a4=-1,a5=-2,a6=-1,a7=1,a8=2,……

所以{an}是周期為6的周期數(shù)列,又

2 024÷6=337……2,

所以a2 024=a2=2.

由例4可以看出,當(dāng)特征方程無(wú)實(shí)數(shù)根時(shí),數(shù)列{an}是一個(gè)周期數(shù)列[2].這一結(jié)論具有普遍性,在這里省略證明.

4 特征方程法的解法總結(jié)

根據(jù)例2～例4的解答過(guò)程可以將相鄰三項(xiàng)線(xiàn)性遞推關(guān)系數(shù)列通項(xiàng)公式的求解歸納如下：

(Ⅰ)當(dāng)特征方程有兩個(gè)不相等的實(shí)根時(shí)

(1)寫(xiě)出特征方程并求出兩根x1,x2;

(2)設(shè)an=c1·(x1)n+c2·(x2)n;

(3)將a1,a2的值代入,求出系數(shù)c1,c2,進(jìn)而寫(xiě)出數(shù)列{an}的通項(xiàng)公式.

(Ⅱ)當(dāng)特征方程有兩個(gè)相等的實(shí)根時(shí)

(1)寫(xiě)出特征方程并求出根x;

(2)設(shè)an=(An+B)·xn;

(3)將a1,a2的值代入,求出系數(shù)A,B,進(jìn)而寫(xiě)出數(shù)列{an}的通項(xiàng)公式.

(Ⅲ)當(dāng)特征方程無(wú)實(shí)數(shù)根時(shí)

分別計(jì)算前幾項(xiàng)的值,判斷數(shù)列{an}的周期性,進(jìn)而求出{an}的通項(xiàng)公式.