王照良,張旭陽

(河南理工大學(xué) 數(shù)學(xué)與信息科學(xué)學(xué)院,河南 焦作 454000)

在數(shù)據(jù)分析中,有些變量可能無法準(zhǔn)確收集,如血壓,智力,肥胖等,在測量過程中會受到一定程度的影響,就會產(chǎn)生測量誤差.這導(dǎo)致了一類測量誤差(errors-in-variables)模型.記X∈p為真實模型中的解釋變量,Y∈p為響應(yīng)變量,那么線性回歸模型有如下形式

Y=XTβ+ε,

(1)

其中β∈p為未知參數(shù)向量,ε是隨機誤差.在測量誤差模型中,解釋變量X是潛在變量,常常不能被直接觀測.本文考慮線性測量誤差或加性誤差模型,即

W=X+U,

(2)

其中變量W是可以直接觀測的,而U為零均值的測量誤差.假設(shè)測量誤差U與(Y,X)不相關(guān),Cov(U)=∑u.為了模型的可識別性,進一步假設(shè)∑u已知.如果∑u未知,我們可以利用文獻 [1]中提出的重復(fù)測量技術(shù),估計β是我們感興趣的事情.

正如文獻[2]中指出,如果忽略測量誤差而直接用W代替X,所得到的估計量和推斷可能有偏差和不一致.因此,調(diào)整測量誤差的存在對于準(zhǔn)確描述真實解釋變量和感興趣的響應(yīng)變量之間的關(guān)系很重要.測量誤差模型的研究可以追溯到文獻[3],文獻中提出了測量誤差線性模型參數(shù)的有效估計量.文獻[4]和[5]系統(tǒng)研究了測量誤差模型和數(shù)據(jù)分析,概述了存在測量誤差的情況下更現(xiàn)代的估計方法.當(dāng)X,U,ε的分布已知時,可以使用似然方法估計參數(shù),具體可以參見文獻 [6].實現(xiàn)這些似然方法通常需要使用數(shù)值方法近似計算,如高斯積分或蒙特卡羅積分.文獻[7]使用矩方法來估計線性測量誤差模型,考慮了基于三階矩和四階矩的參數(shù)估計,并發(fā)現(xiàn)這些估計量有很大的方差.關(guān)于測量誤差模型的其他研究成果可參見文獻 [8-11].

在某些情況下,一些關(guān)于回歸系數(shù)的先驗信息可以從外部樣本獲得.這些信息可能有不同的來源,如過去的經(jīng)驗或?qū)嶒炚吲c實驗的長期聯(lián)系,過去進行的類似實驗等.使用這些信息可以提高估算器的效率.在線性回歸分析的背景下,當(dāng)這些信息以精確的線性約束的形式使用時,受約束的最小二乘估計量比普通最小二乘估計量更有效,如 [12].在許多重要的統(tǒng)計應(yīng)用中,由于大量數(shù)據(jù)驅(qū)動的原因,模型(1)的參數(shù)分量可能會受到一些附加約束條件的約束.例如,[13]和 [14]中引入了對參數(shù)向量β的精確線性約束,構(gòu)造了附加約束性條件下的修正拉格朗日乘子檢驗統(tǒng)計量.在本文中,我們假設(shè)參數(shù)向量β滿足以下線性約束:

Hβ=d,

(3)

其中H是一個k×p階的已知矩陣,rank(H)=k,d是一個k×1階的已知向量.[15]研究了基于約束條件(3)的模型(1)的估計.文獻中沒有考慮存在測量誤差的情況以及估計的有效性.當(dāng)解釋變量X存在加性誤差時,[15]提出的方法會導(dǎo)致參數(shù)分量的估計是一個有偏估計量.為此,我們考慮基于約束條件(3)的模型(1) 和(2),并研究估計和檢驗問題.當(dāng)H取到不同的矩陣時,我們可以得到不同的約束估計.實際上,參數(shù)的受約束估計起到了降維的作用.

本文在線性約束(3)的基礎(chǔ)上,研究了參數(shù)分量中有測量誤差(2) 存在的線性模型(1)的估計問題.我們提出了受約束的糾偏最小二乘估計量,并在一定的正則條件下建立了得到的估計量的漸近性質(zhì).最后通過模擬對所提出的方法進行了說明.

本文用M表示矩陣,A表示向量,記A?2=AAT,其中AT表示向量的轉(zhuǎn)置,矩陣類似.這一節(jié)提出了研究問題,第2節(jié)將闡述主要估計方法和提出估計量的漸近性質(zhì).第3節(jié)通過數(shù)值模擬研究了所提方法的有限樣本性質(zhì).第4節(jié)給出簡要結(jié)論.第5節(jié)給出相關(guān)理論證明.

1 估計方法和漸近性質(zhì)

1.1 受約束的糾偏最小二乘法

假設(shè)(Y1;X1,W1),...,(Yn;Xn,Wn)是來自測量誤差線性模型

(4)

的一個獨立同分布的隨機樣本.在模型(4)中,X是潛在的不可觀測的p維解釋變量,W是p維可觀測變量,Y為響應(yīng)變量,ε為模型誤差且期望為0,方差為σ2,U為測量誤差.本文假定E(U)=0和Cov(U)=∑u,且∑u已知.矩陣∑u可奇異,這意味著允許某些分量不存在測量誤差,未被污染觀測.

假設(shè)X可以被直接觀測到,即不存在測量誤差,則理論上β可通過最小化E‖Y-XTβ‖2得到,通過求導(dǎo)可得最優(yōu)的估計方程為

E[X(Y-XTβ)]=0.

然而,測量誤差模型(4)中的X是不可觀測的,如果直接用W來替換X,最小化E‖Y-WTβ‖2,則有

E[W(Y-WTβ)]=-∑uβ≠0.

因此,直接用觀測變量W來替換潛在變量X,所得估計是有偏的,甚至是不相合的.注意到,

E[W(Y-WTβ)+∑uβ]=0,

于是,可通過最小化如下的偏差校正的目標(biāo)函數(shù)

Qn(β)=‖Y-WTβ‖2-nβT∑uβ.

(5)

來估計未知參數(shù)β.式(5)右端的第二項-βT∑uβ是一個負的懲罰運算,其作用是削減由測量誤差帶來的影響.也就是說,當(dāng)它是一個標(biāo)量時,為了在絕對值中低估β,必須取更大的β來校正衰減,而不是進一步皺縮它接近于0.因此,它起一個校正的作用.

通過簡單計算,最小化(5)可以得到β的偏差校正估計量為

(6)

其中Y=(Y1,Y2,...,Yn)T,W=(W1,W2,...,Wn)T.

如果能夠獲得感興趣的回歸系數(shù)的先驗信息,則利用這些先驗信息可以提供更好的估計,如果我們忽略了先驗信息,可能會增加對數(shù)據(jù)誤讀的可能性.對模型(1)和(2),如果感興趣的參數(shù)β滿足精確的線性約束條件(3),本文提出通過最小化如下偏差校正的拉格朗日函數(shù)

F(β,λ)=(Y-Wβ)T(Y-Wβ)-nβT∑uβ+2λT(Hβ-d)

作為β的估計量.

利用函數(shù)極值的一階條件,對函數(shù)F(β,λ)分別關(guān)于β和λ計算偏導(dǎo)數(shù),并且將結(jié)果分別設(shè)為零,即得到如下的估計方程

(7)

通過計算,可以得到方程(7)的解為

(8)

其中S=WTW-n∑u.

求未知參數(shù)β滿足約束條件(3)的一致估計量,還可以通過如下帶約束的極值問題

s.t.Hβ=d

1.2 漸近性質(zhì)

為了得到估計量的漸近性質(zhì),我們首先給出下列正則條件.

C1.矩陣∑x=E(XXT)非奇異.

C2.隨機樣本(Y1;X1,W1),…,(Yn;Xn,Wn)獨立同分布.

C3.假定E(ε)=0,D(ε)=σ2且ε與X不相關(guān).

C4.假定E(U)=0,且U與(X,Y,ε)不相關(guān).

引理1假設(shè)條件C1-C4成立,當(dāng)n→∞時,則

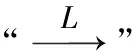
∑1=E{ε-UTβ}?2∑x+E{(UUT-n∑u)β}?2+σ2∑u

定理1假設(shè)條件C1-C4成立,當(dāng)n→∞時,則

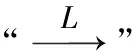
定理2假設(shè)條件C1-C4成立,當(dāng)n→∞時,則

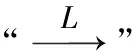
∑3=HT[HHT]-1H.

2 數(shù)值模擬

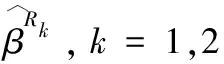
為實施模擬,利用模型(1)和(2)產(chǎn)生模擬數(shù)據(jù).考慮p=4的情形,其中β=(1.5,2,1,1.5)T.顯然參數(shù)β滿足線性約束Hβ=0,其中矩陣H為

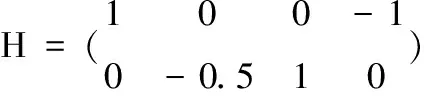
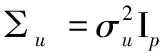
為了評估估計量的有限樣本性能,分別在樣本容量n=50,100,200下通過1000次重復(fù)模擬計算偏差(Bias),標(biāo)準(zhǔn)差(SD) 和均方誤差(MSE).模擬旨在研究不同樣本容量n,不同測量誤差水平∑u和X各分量之間不同相關(guān)性設(shè)置下的5種估計方法的表現(xiàn).表1和表2分別展示了當(dāng)∑x=Ip和∑x=(0.5|i-j|)1≤i,j≤p時的模擬結(jié)果.

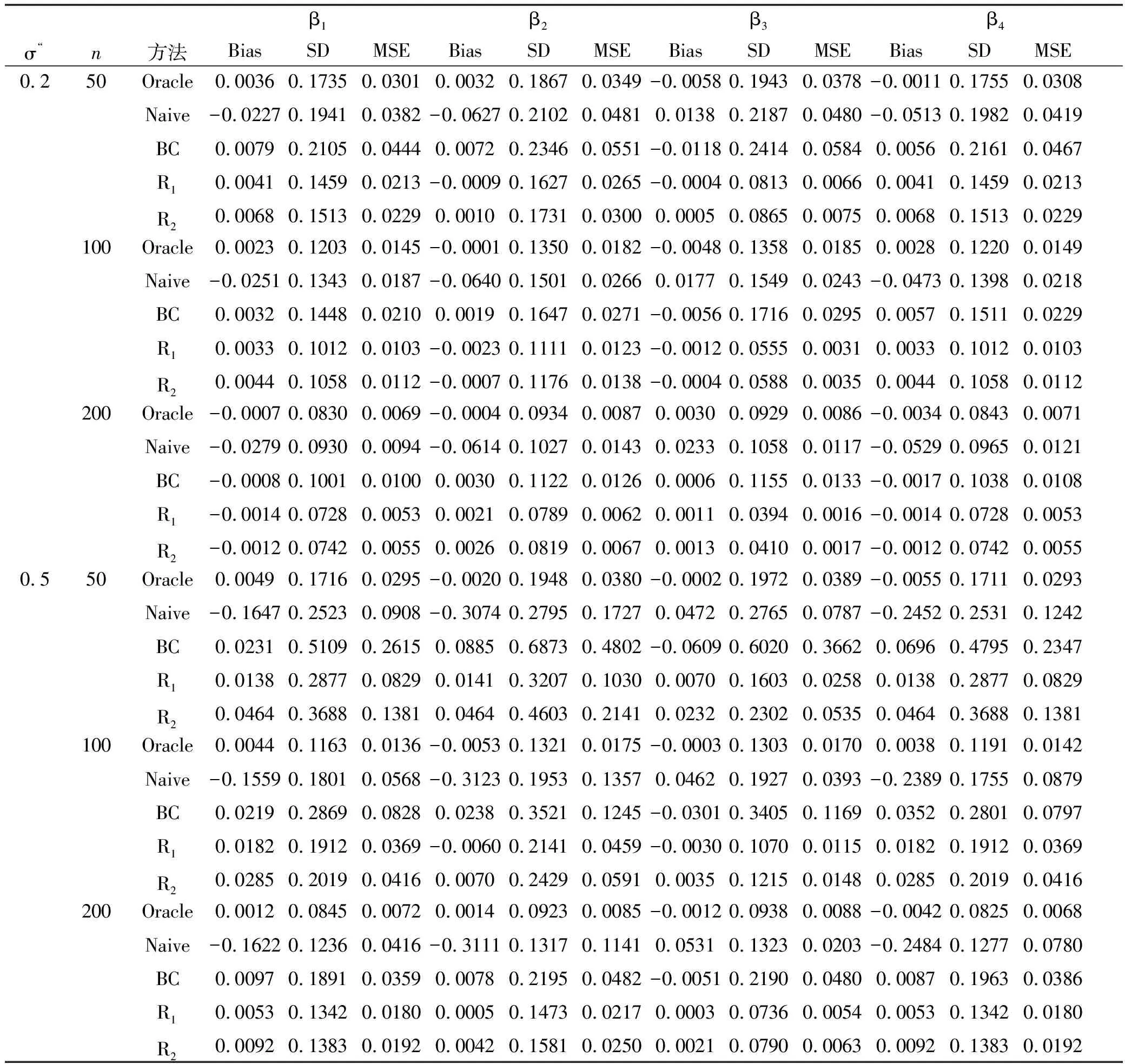
表2 當(dāng)∑x=(0.5|i-j|)1≤i,j≤p時,5種估計方法的模擬結(jié)果

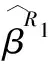
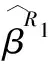
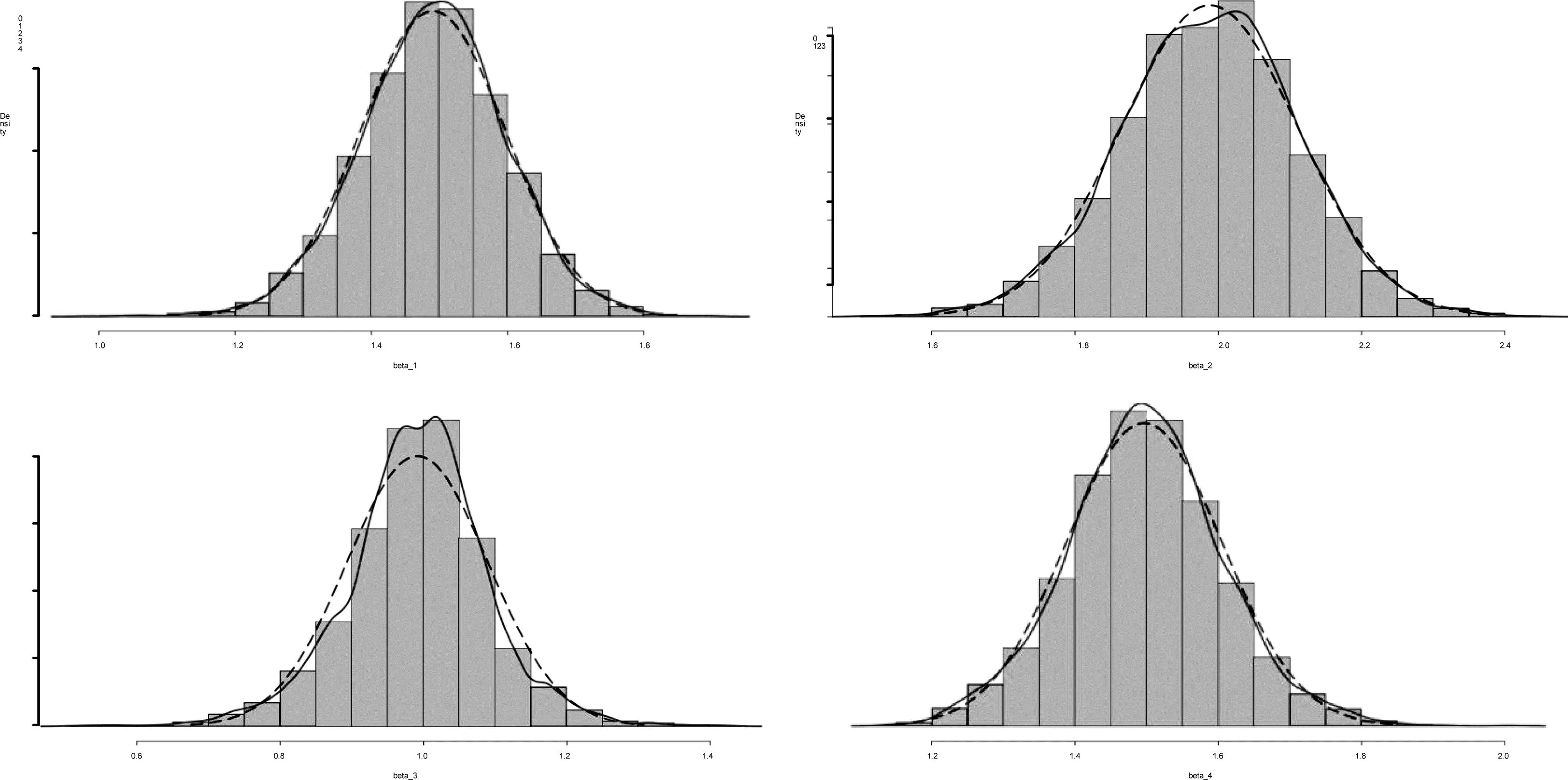
圖1 當(dāng)∑x=Ip,σu=0.2,n=100時,基于1000次模擬計算估計量的直方圖及密度估計曲線

3 結(jié) 論

本文考慮了精確線性約束條件(3) 下測量誤差線性回歸模型的統(tǒng)計推斷問題.結(jié)合偏差校正最小二乘法和拉格朗日乘子法,對模型中的參數(shù)向量β提出了受約束的糾偏最小二乘估計方法.在一定的正則性條件下,證明了所提出的參估計量的漸近正態(tài)性.此外,通過MonteCarlo模擬研究了所提出方法的有限樣本性能.理論結(jié)果和模擬結(jié)果均表明所提出的估計量優(yōu)于其他類型的估計量.

4 定理證明

4.1 引理1的證明

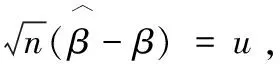
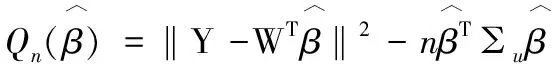
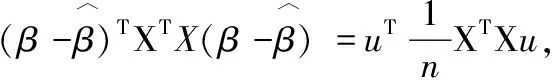
其中R是與u無關(guān)的項.

由ε,U和X的獨立性,以及中心極限定理,可知

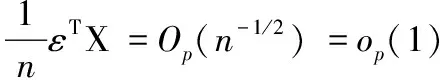
由條件C1和大數(shù)定律可得,

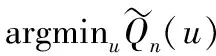
其中

由所給條件和大數(shù)定律可得,

此外,容易計算

E{XT(ε-Uβ)+UTε-(UTU-n∑u)β}=0.

根據(jù)中心極限定理,可得

∑1=E{XT(ε-UTβ)+UTε-(UUT-n∑u)β}?2=E{ε-UTβ}?2∑x+E{(UUT-n∑u)β}?2+σ2∑u

最后,根據(jù)Slutsky定理可知

引理1得證.

4.2 定理1的證明

證明 首先定義J=I-S-1HT[HS-1HT]-1H,其中

S=WTW-n∑u.

(9)

根據(jù)(8),簡單計算可知

其中J0=I-∑x-1HT[H∑x-1HT]-1H.

由Slutsky定理和引理1,可得

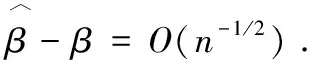
綜上,

定理1得證.

4.3 定理2的證明

類似于定理1的論證,可以完成定理2的證明.因此,我們省略了證明的細節(jié).