PROPORTION OF DISTINCT ZEROS OF A DIRICHLET L-SERIES?
Xinhua QIN()Xiaosheng WU()
School of Mathematics,Hefei University of Technology,Hefei 230009,China
E-mail:qxh0916@mail.hfut.edu.cn;xswu@amss.ac.cn
Abstract By studying the distribution of zeros of combinations of a Dirichlet L-function and its first-order derivative,we prove that every Dirichlet L-function has more than 66.7934%distinct zeros.
Key words simple zeros;distinct zeros;Dirichlet L-function
Dedicated to Professor Banghe LI on the occasion of his 80th birthday
1 Introduction
Letχ(modq)be a Dirichlet character.For Re(s)>1,a DirichletL-function is defined as

It is known that all non-trivial zeros ofL(s,χ)lie in the critical area {s=σ+it:0<σ<1}.We writeN(T,χ)as the total number of zerosρ=β+iγofL(s,χ)with 0<β<1 and|γ|≤T.For a primitive character,it is well-known that

and the non-primitive character case shares the same zeros with the corresponding primitive character case.It is generally believed that all of these zeros are simple;this is known as the Simple Zeros Conjecture.For the Riemann zeta-function,there is a long history on the issue;see [1,4,5,10]for examples.The best result known so far is that more than 40.74%of zeros are simple;this was proven by Wu [17],and also independently by Pratt,Robles,Zaharescu,and Zeindler [13],based on Levinson’s method(see [5,11]for the Levinson’s method).
The number of distinct zeros means counting each zero precisely once without regard to the multiplicity.The Simple Zeros Conjecture is equivalent to all zeros being distinct.For the Riemann zeta-function,Farmer [8]proved that at least 63.952%of zeros are distinct,which results from the proportions of the simple zeros of derivatives of the Riemannξ-function.By studying the distribution of zeros of combinations of the Riemann zeta-function and its firstorder derivative,Wu [15]proved a larger proportion:66.03%.
Estimating the error term with the large sieve,Bauer [2]deduced an asymptotic formula for a twisted mean value of a DirichletL-function.Then he obtained that more than 35.62%of zeros are simple and that more than 61.347%of zeros are distinct.Results in [2]are weaker than the Riemann zeta-function case in the same period,since the largesieve only works with a short mollifier.Wu [17]proved that a more general mollifier(Feng’s mollifier [9]),not only for the Riemann zeta-function but also for a DirichletL-function,can be taken as long asθ <4/7,and this provides that more than 40.74%of zeros are simple.
For the family of all DirichletL-functions,there are much better results.In 2013,Conrey,Iwaniec,and Soundararajan [6]deduced the Asymptotic Large Sieve and then successfully used it in the study of zeros.In asymptotic terms,they proved in [7]that more than 58.65%of zeros of the family of DirichletL-functions are simple and on the critical line.Wu [16]proved that the simple zeros are more than 60.26%,and that the distinct zeros are more than 80.13%,but these zeros are not necessarily on the critical line.
In this work,we use the method of [15],in combination with the mollifier of [17],to study the number of distinct zeros for a DirichletL-function.We obtain that more than 66.793%of zeros are distinct,which is an improvement upon Bauer’s 61.347%in [2],and also upon the proportion 66.03%in [15]for the Riemann zeta-function.Letting

we present our result in the following theorem:
Theorem 1.1Letχbe a Dirichlet character moduloq.For largeTwith logq=o(logT),we have that
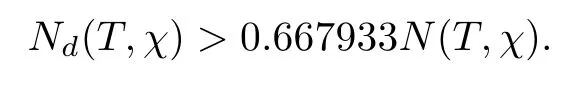
LetG(s,χ)be a complex-valued function of form
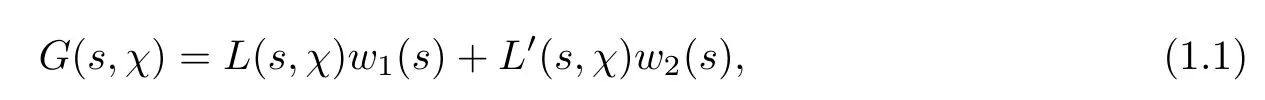
wherew1(s)andw2(s)are any two functions that are analytic in the critical area.As noted in [15],L(s,χ)should have less multiple zeros in an area ifG(s,χ)has less zeros in the same area.Thus,Theorem 1.1 should be proven with several appropriateG(s,χ),whose areas with less zeros can cover the whole critical area.
We split the critical area into the right-hand side and the left-hand side according to the critical line.To the right-hand side,let D be a closed rectangle with vertices?iT,3?iT,+iT,3+iT.Denote byNG(D,χ)the number of zeros ofG(s,χ)in D,including the zeros on the left boundary.We are interested inG(s,χ)with less zeros in D.
Theorem 1.2Letχbe a primitive character moduloq.For largeTwith logq=o(logT),there is someG(s,χ)of the form(1.1),which gives that
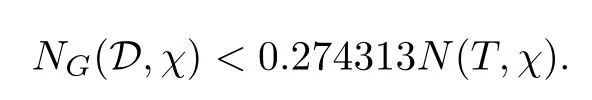
Let
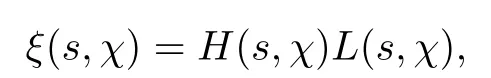
with
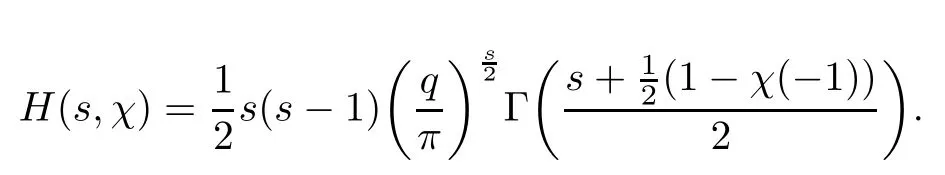
To the left-hand side,we appeal to the first-order derivative ofξ(s,χ),which is of course a specialG(s,χ)of the form(1.1).Denote byNξ′(T,χ)the number of zeros ofξ′(s,χ)in the critical area with|t| see also [16,Lemma 1.7].The symmetry of zeros ofξ′(s,χ)implies that the more zeroswe have on the critical line,the better result we will get.Denote byNξ′,c(T,χ)the number of zeros ofξ′(s,χ)on the critical line. Theorem 1.3Letχbe a primitive character moduloq.For largeTwith logq=o(logT),we have that This improves on the proportion 0.847212 in [2]forξ′(s,χ),and also improves on the proportion 0.86957 in [15]forξ′(s). NotationSince a DirichletL-function to a non-primitive character shares the same nontrivial zeros as the DirichletL-function to the corresponding primitive character,it is enough to prove the theorem for primitive characters.Thus,we will always assume thatχis a primitive character moduloqin what follows.We will use theε-convention to denote a small positive real number,whose value may vary from line to line.We should keep in mind thatTis large enough with logq=o(logT).The Euler function?(q)denotes the number of positive integers less than and prime toq. In this section,we prove Theorem 1.1 with Theorems 1.2 and 1.3.For a complex-valued functionf,we count the zeros offwith multiplicity minus one,and say it is the number of additional zeros caused by multiplicity.This classes the total zeros as distinct zeros and additional zeros caused by multiplicity.Since every zero ofL(s,χ)with multiplicitym≥2 is also a zero ofG(s,χ)with multiplicity≥m?1,the additional zeros ofL(s,χ)are not more than the zeros ofG(s,χ)in any region.With several appropriateG(s,χ),whose areas with less zeros cover the whole critical area,we can prove Theorem 1.1 by counting the zeros in their respective areas. We partition the critical area ofL(s,χ)into the left-hand side(Re(s)<1/2)and the right-hand side(Re(s)≥1/2),and then for each side we choose an appropriateG(s,χ).To the left-hand side,we takeG(s,χ)=ξ′(s,χ).The functional equation forL(s,χ)says that where To the right-hand side,we takeG(s,χ)as in Theorem 1.2.With estimates in Theorem 1.2 and Theorem 1.3,we have that and thereby accomplish the proof. LetR>0 be a constant and let Forj=1,2,we write that withy=Tθ,0< θ <4/7 and wherePji(x)are some polynomials satisfying thatPji(0)=0 andPj1(1)=1,to be specified later. To prove Theorem 1.2 and Theorem 1.3,we need the asymptotic mean value result forL(s,χ)proved in [17,Proposition 3.1].The original mollifier in [17]owns a restrictionp≤y3/4on the volume ofpinaj(n).This can be removed for the special mollifier of form(2.1)with the help of the technique in [13];see also the Remark in the end of [17,Section 1]. Lemma 2.1Letχbe a primitive character(modq)with logq=o(logT)andα=a/L,β=b/L witha,b?1.Suppose that?=T1? ηwithη >0,y=Tθwith 0< θ <4/7,ands0=1/2+iwwithT≤w≤2T.Forj1,j2=1,2,let Then we have,uniformly ina,b,andw,that We writegj1j2(a,b)in another form for easy of application.Since and ass→0,there is with We take withB1(s,χ)andB2(s,χ)being defined as in(2.1).To counter the zeros ofG(s,χ)in D,we appeal to Little wood’s formula.The treatment will be processed in a standard way,so we only sketch it here.We introduce another closed rectangle D1which is a little larger than D to the left side;it has vertices atσ0?iT,3?iT,σ0+iT,3+iTwith A direct calculation shows that and and thusG(3+it,χ)0.After using a standard technique,we can avoid zeros on the edge and then apply Littlewood’s formula(to see [12])to get that where dist(ρ)is the distance ofρto the left edge of D1. To the left-hand side of(3.4),all terms except the first one will be bounded by an error termO(T/L).We consider the last two terms first.Asq?Tεandσ0>?ε,it is obvious thatψi(s,χ)?T,L(s,χ)?T,L′(s,χ)?T,and thusG(s,χ)?T2.In virtue of this bound and Jensen’s theorem,a familiar method as to [14,Section 9.4]shows that For the second term,we note from(3.2)and(3.3)that Also,the logarithm ofψ1(s)is well bounded fora1(1)=1;more precisely, and thus logψ1(s)is analytic forσ≥3.By the Cauchy theorem, Taking the real part in both sides above,we have that Applying this with(3.6)in(3.5)gives that In conclusion,(3.4)evolves into Then,by(3.8), The concavity of the logarithm function gives that To apply Lemma 2.1,weconvert the integral to the required form with the following lemma,which follows exactly as in Balasubramanian,Conrey,and Heath-Brown [3,Section 3]: Lemma 3.1For?=T1? η,η >0,we have,uniformly inwwithT≤w≤2T,that Applying the lemma with the definition ofG(s,χ),we have that By Lemma 2.1, An asymptotic formula for Σ(α,β)has been provided in [17,Section 6].With with Σi1i2(a,b)being some integrals,as follows: Here we have used the simple integral equality to simplify the original expressions in [17,Section 6].Applying these in(3.11)and then(3.10)and(3.9),successively,we can get an upper bound forNG(D,χ)with appropriate polynomialsPji(x),as well as a constantR.Takingθ=4/7?ε,R=1.021, Hence,we obtain Theorem 1.2. For convenience,we have limited the degree of polynomials to at most 3.Then,optimizing the function by Mathematica gets the coefficients. Similarly to(2.1),we write that withy=Tθ,0< θ <4/7 and wherePi(x)are some polynomials withPi(0)=0 andP1(1)=1,to be specified later. For a real constantcand a real polynomialQ(x)satisfying letV(s)be a differential polynomial ofL(s,χ);that is to say, In virtue of the well-known Levinsion method and an argument with the Little wood formula as above,one may deduce in a standard way the estimate For details of this,one may see [15],which was prepared for the Riemann zeta-function,but which also works here. Thus,after applying Lemma 3.1 and then Lemma 2.1,we have that with Σ(α,β)being defined as in(2.2). Also,an asymptotic formula for Σ(α,β)can be deduced from [17,Section 6].We write that withi=1,2 and Then,

1.1 Proof of Theorem 1.1

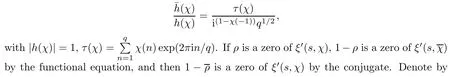

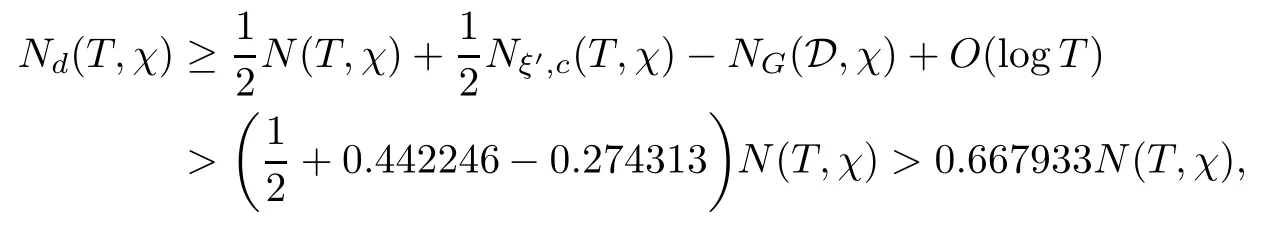
2 Twisted Mean Value of L(s,χ)


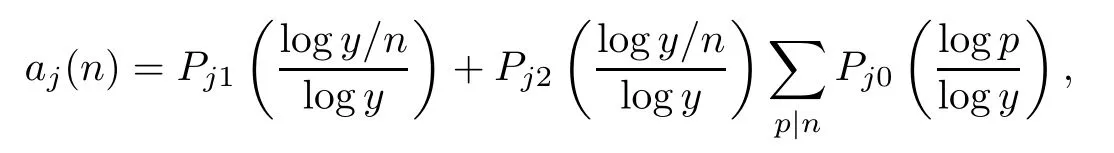


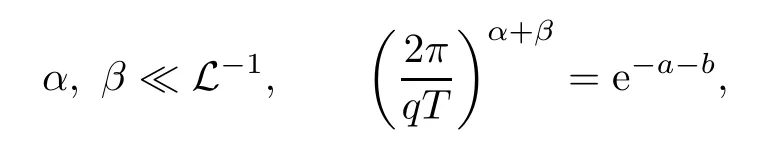

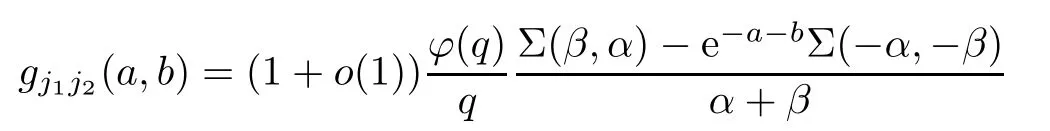

3 Proof of Theorem 1.2
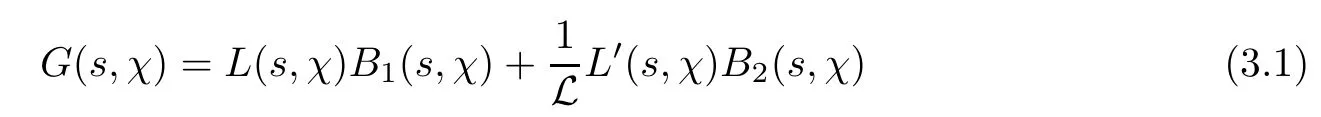



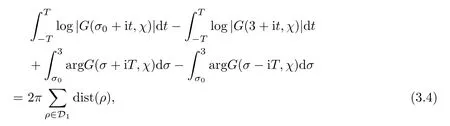


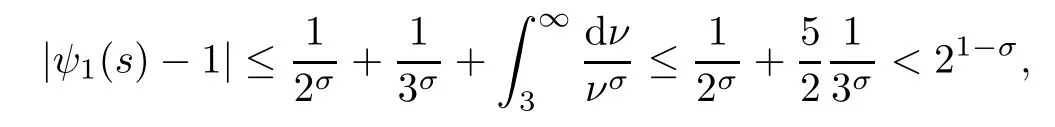
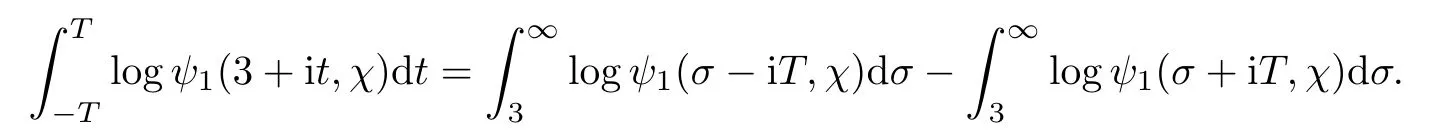
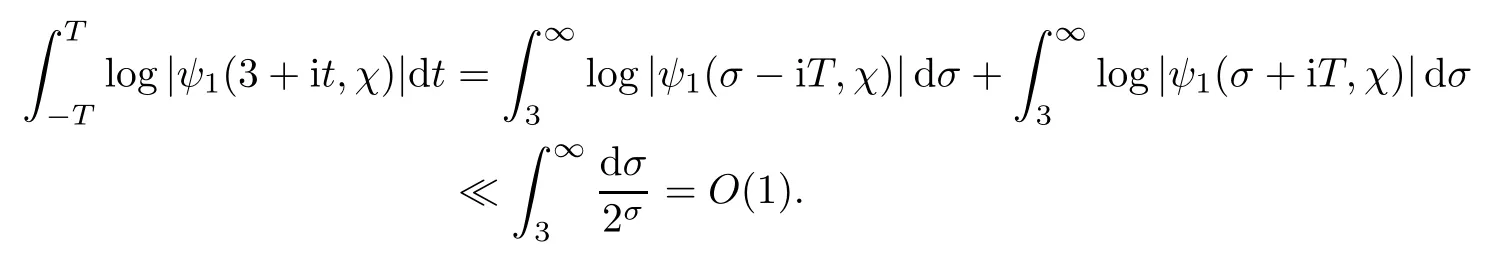



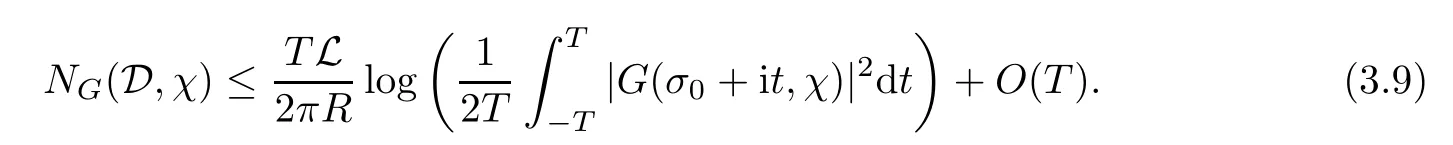
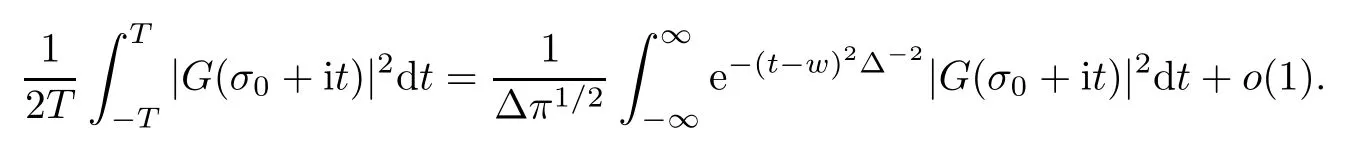
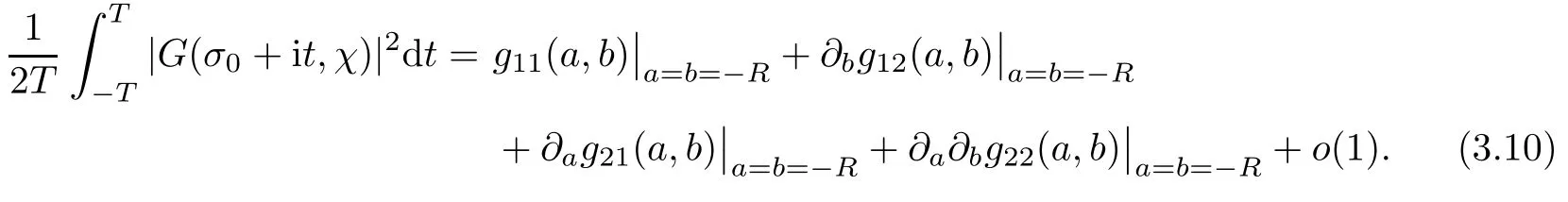

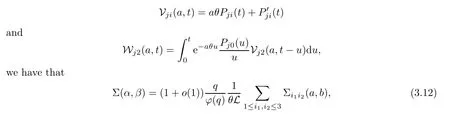

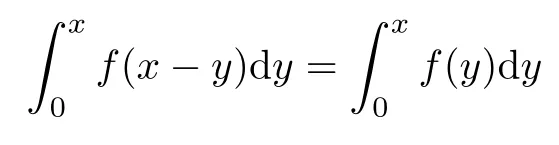

4 Proof of Theorem 1.3


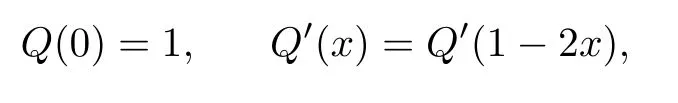
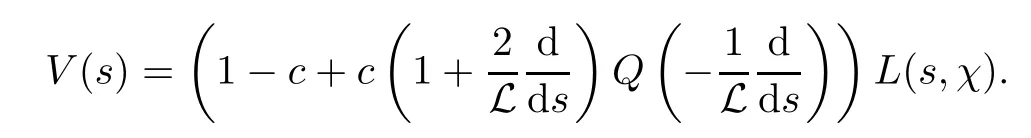
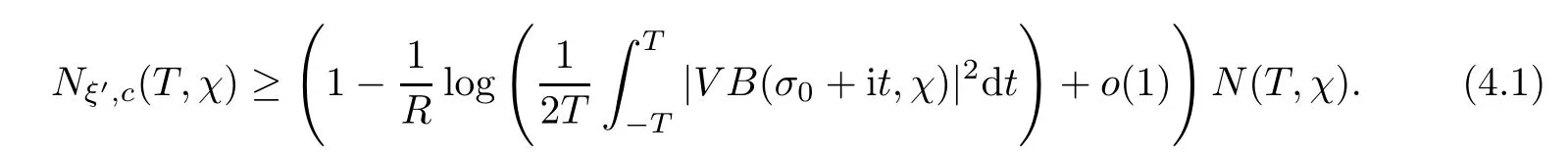
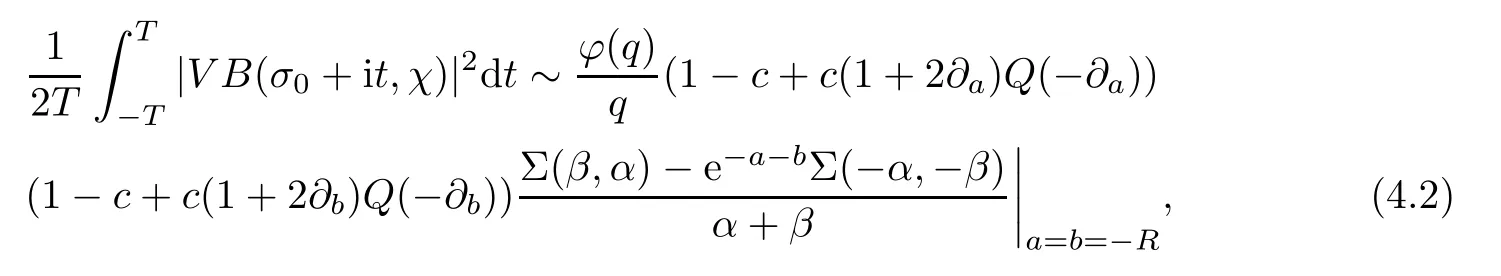

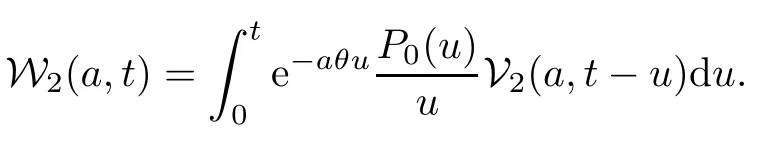

 Acta Mathematica Scientia(English Series)2022年6期
Acta Mathematica Scientia(English Series)2022年6期
- Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL WELL-POSEDNESS OF A PRANDTL MODEL FROMMHD IN GEVREY FUNCTION SPACES?
- L 2-CONVERGENCE TO NONLINEAR DIFFUSION WAVES FOR EULER EQUATIONS WITH TIME-DEPENDENT DAMPING?
- SYMBOLIC COMPUTATION FOR THE QUALITATIVE THEORY OF DIFFERENTIAL EQUATIONS?
- OPINION DYNAMICS ON SOCIAL NETWORKS?
- ON ACTION-MINIMIZING SOLUTIONS OF THE TWO-CENTER PROBLEM?
- SOME RESULTS ON HEEGAARD SPLITTING?
