OPINION DYNAMICS ON SOCIAL NETWORKS?
Xing WANG() Bingjue JIANG() Bo LI()
1.KLMM,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China
2.School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
E-mail:wangxing17@amss.ac.cn;jiangbingjue18@mails.ucas.ac.cn;libo@amss.ac.cn
Abstract Opinion dynamics has recently attracted much attention,and there have been a lot of achievements in this area.This paper first gives an overview of the development of opinion dynamics on social networks.We introduce some classical models of opinion dynamics in detail,including the DeGroot model,the Krause model,0?1 models,sign networks and models related to Gossip algorithms.Inspired by some real life cases,we choose the unit circle as the range of the individuals’opinion values.We prove that the individuals’opinions of the randomized gossip algorithm in which the individuals’opinion values are on the unit circle reaches consensus almost surely.
Key words opinion dynamics;social networks;graph theory
Dedicated to Professor Banghe LI on the occasion of his 80th birthday
1 Introduction
As a part of a community,we interact with other people and exchange opinions with others everyday.We have our own opinions about hot topics in the world,and we also influence and are influenced by other people.Some people are easily influenced by others,while some are stubborn.Some people are eager to find someone with the same opinions,while some people are more likely to interact with those who have different opinions [1].There are people who are submissive to social norms,but there are also people who are rebellious [2].We can see that all different kinds of opinions spread among people throughout society,and these opinions interact with each other in some way.Opinion dynamics is a field for analyzing the above phenomena.Over the past several decades,there has been growing interest in opinion dynamics as an interdisciplinary study in fields such as control theory,sociology,economics,and biology [3–8].
As networks grow more and more complex,distributive algorithms have become more and more important.Gossip protocol,in which information exchange is only carried out in pairs between two nodes,has been widely used to aggregate and spread information distributively,and has been used in distributed computation,optimization,and social networks [9–11].Gossip algorithms usually consist of two parts:the rules for the selection of pairs of nodes,and updates on the values of the pair of nodes.The name for this algorithm comes from the office gossip.Now,gossip protocol has been used to provide distributive computation in fields like optimization,control theory,signal processing,and artificial intelligence [12–14].
Here,we give a review of the basic models in opinion dynamics.The aim of this paper is to introduce the basic models in opinion dynamics and give some new insights or even extend upon some of these.In Section 2,we introduce some classical models in opinion dynamics,including the DeGroot model,the Krause model,signed networks,and fashion games.Models relevant to gossip algorithmsarediscussed in Section 3.In the last part of Section 3,weprovide a new model in which opinion values are defined on the unit circle instead of by real numbers.We categorize these models in Section 4.
2 Models of Opinion Dynamics
In this section,we introduce some classical models in opinion dynamics.
2.1 DeGroot Mod el
The DeGroot model,the basic model of opinion dynamics,was proposed by DeGroot as early as 1974[15].The DeGroot model describes the process in which agents in a social network change their own opinions by informing each other of their opinions,collecting all of opinions they received,and finally forming a common opinion.Consider a social network described by a graphG=(V,E)consisting ofnagents.The edge of the graph is used to indicate the interactive relationship between the nodes.If agentsiandjcan interact with each other,or in other words,can exchange information,then {i,j}∈E.In graph theory,we also say that agentiand agentjare neighbors.At timet,each agent has a specific opinion,xi(t)∈R,t=0,1,···.Since each agent has different background,their opinions are also different,and they usually reflect their own information.If an agentiis informed of the opinionsxj(t),j=1,···,n,j/iof all their neighbors in the social network,then agentiwill naturally change their opinions to suit the opinions and judgments of other members.Letwijdenote the weight that an agentiassignsto an agentjwhen they changestheir opinion;this is chosen by the individual according to the relative importance of the opinion to all members in the network(including themselves).Then at the timet+1,agenti’s opinions will be updated to
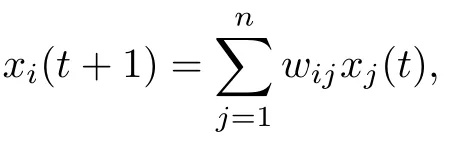
wherewij≥0 and=1.Letx(t)=(x1(t),···,xn(t))Tand letWbe the matrix where the(i,j)-entry iswij,i=1,···,n,j=1,···,n.Then the above opinion update rule can be expressed in the following form:

Obviously,Wis a random matrix,i.e.,the sum of each row is 1.The DeGroot model depicts the interaction between individuals in the social networkG=(V,E),and the opinion of an agentiat each update moment is the weighted average of its own opinion and the opinions of all its neighbors at the previous moment.Since it is assumed that the network topology does not change with time in the process of opinion updating,the DeGroot model is called a time-invariant social network model.Furthermore,given an initial opinionx(0),the opinion dynamics of the social network can be expressed as

which is only related to the weight that each agent in this network gives to all members of the entire social network.
The model is convergent if and only if for any initial opinionx(0),there is an opinion vectorx?∈Rnsuch that

The model can reach consensus if and only if,for any initial opinionx(0),there is a real valueasuch that
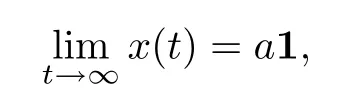
where1is the vector with all entries being 1.It can be seen that consensus is a special case of convergence;i.e.,consensus can only be reached when thencomponents ofx?all converge to the same valuea.
According to(2.1)and(2.2),the opinion evolution process on the social networkGis a discrete time Markov chain,and the random matrixWis its state transition matrix.DeGroot [15]gives two sufficient conditions for consensus.First,if there is a positive integerksuch that at least one column of the matrixWkis positive,then each agent’s opinion in the social networkGcan reach consensus.Second,if all the states of the Markov chain are positive recurrent,irreducible,and aperiodic,then agents in the social networkGcan reach consensus.Furthermore,when consensus is reached,the common opinion of the social network can be precisely calculated.
2.2 Krause Model
In the DeGroot model,the topology of the social network is fixed;that is to say,the influence of the social network remains constant.In real life,however,the influence between people is always changing.The Krause model [16,17]and its extensions [18]are time-variant models in social networks.
Just as in the DeGroot model,we use the real valuexi(t)to represent the opinions of agenti.However,each agent in the Krause model only interacts with those agents it regards as necessary in order to communicate.Specifically,each agentihas a confidence bound,denoted byεi.The opinions of agentiare only influenced by those agents whose opinions differ from agenti’s opinion by no more thanεi.Therefore,for agenti,the agents that will have an influence on its opinion at timetcan be represented by the setI(i,t),that is

where|·|represents the absolute value of a real number.Having these notations,the opinion formation of agentican be described as
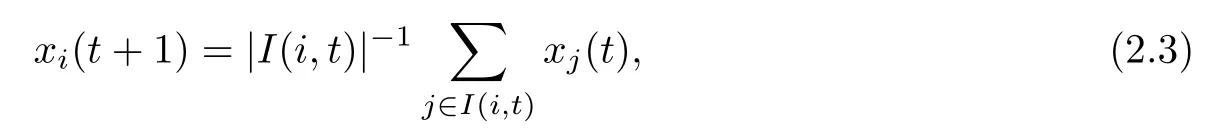
where|I(i,t)|is the number of elements in the finite setI(i,t);that is,agentiadjusts their opinion in periodt+1 by taking a weighted average with weight|I(i,t)|?1for the opinion of agentj∈I(i,t)at timet.
Note that,in the Krause model,the agents interacting with agentiat different times are not exactly the same.If a graph is used to represent the interaction between individuals,the graph is constantly changing.This is to say the network topology of the Krause model is not fixed,but that it changes over time.
To simplify,we can assume that the confi dence bound of all agents are equal,i.e.,εi=ε ,i=1,···,n.An important property of the Krause model is that if the opinions of agentiand agentjsatisfy the relationxi(t)≤xj(t)at timet,thenxi(t+1)≤xj(t+1).In other words,the order of agent opinion values does not change over time.Taking advantage of this property,it is possible to renumber the agents so that the order of agent opinion values is consistent with the sequence number of the agents,i.e.,x1(0)≤x2(0)≤···≤xn(0).Using this order relationship,opinion dynamics in the network system can be studied,even if the network topology formed between agents changes over time.
For a sorted opinion vectorx(t)=(x1(t),···,xn(t)),we say that there is a split(or crack)between agentsiandi+1 if|xi+1(t)?xi(t)|> ε.If at timetthere is a split between agentiandi+1,then,according to the update equation(2.3),xi+1(t+1)will not be less thanxi+1(t)andxi(t+1)will not be greater thanxi(t).Thus,if there exists a split at some timet,the split will exist forever aftert.Then the network of opinion dynamics can be split into two smaller independent networks,one consisting of agent 1,···,iand the other consisting of agenti+1,···,n.

Here,the confidence boundεis equal to 1.It can beverified that the properties and convergence results of model(2.3)are also applicable to model(2.4).

Furthermore,Blondel et al.[18]introduced the continuous Krause model to study a society with large population.There are so many people that we can use an interval of real numbers to approximately represent them.More specifically,agents are indexed byI=[0,1],and the opinions of all agents are nonnegative and bounded above by a positive constantL.Letxt(α)be the opinion of agentα∈Iat timet.LetXbe the set of measurable functionsx:I→R,and letXL?Xbe the set of measurable functionsx:I→[0,L].The evolution of the opinions is described by
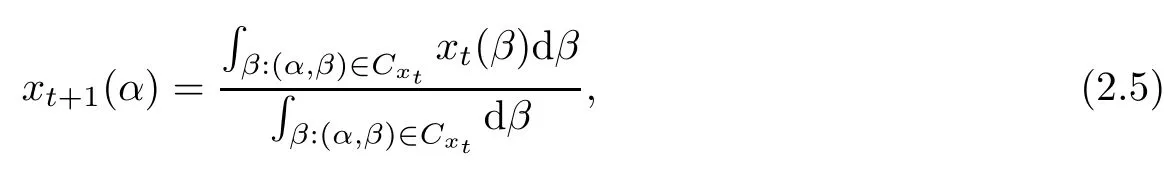
whereCx?I2is defined for anyx∈XbyCx:={(α,β)∈I2:|x(α)?x(β)|<1}.
As in the discrete-agent model(2.3),ifxt(α)≤xt(β)holds for agentsαandβat some timet,then the same relation continues to hold at all subsequent times.Furthermore,if the initial opinion vectorx(0)∈XLonly takes a finite number of values,the continuous-agent model(2.5)coincides with the weighted discrete-agent model(2.4),with the same range of initial opinions,and where each discrete agent’s weight is set as equal to the measure of the set of in dicesαfor whichx0(α)takes the corresponding value.For the continuous Krause model,there are some conjectures which are still unsolved in [18].
2.3 Signed Social Networks
The interactions of agents in the above models are all positive.However,in real world,we are often affected by subjective emotions when we communicate with others.When confronted with trustworthy friends,we are usually willing to listen to their opinions and update our views.On the contrary,when confronted with strangers,we are often suspicious,have a negative attitude,and are reluctant to listen to their opinions;sometimes confrontation even occurs.To this end,signed networks are proposed [19–21].In signed networks,each interaction link has a sign(positive or negative)to reflect whether the agents interacting with each other are friends or not.
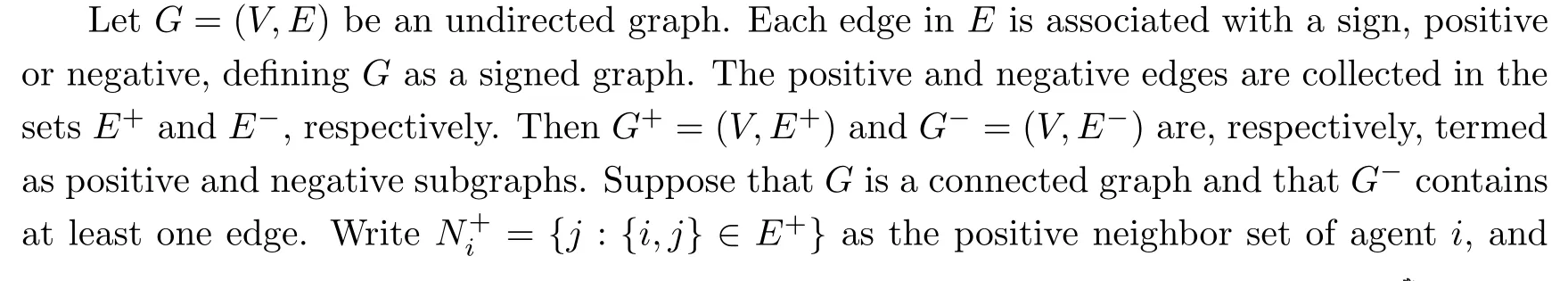

At momentst=0,1,···,each agentihas an opinionxi(t)∈R.The opinion updating rule is specified by the sign of the links.Consider a particular link {i,j}∈E.If the sign of {i,j}is positive,each nodes∈{i,j}updates its opinion by
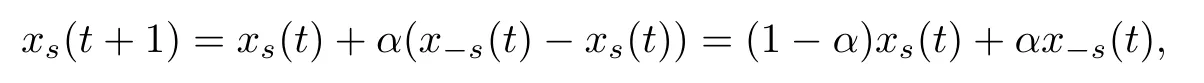
where?s∈{i,j}{s},α∈(0,1).If the sign of {i,j}is negative,each nodes∈{i,j}updates its value by either the opposing rule
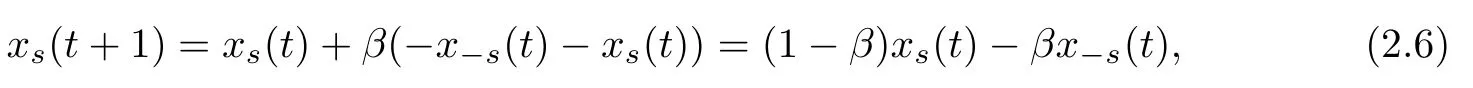
or the repelling rule
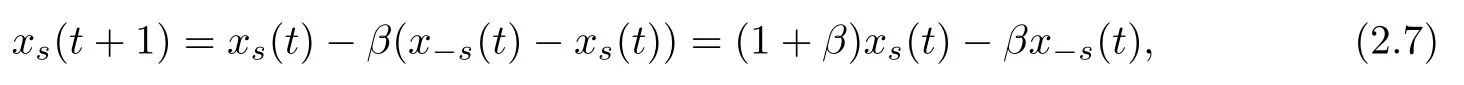
withβ≥0.
It is observed that the positive interaction is consistent with the De Groot model,suggesting that the opinions of trusted social members are attractive to each other.There are two kinds of negative interaction rules:the opposing rule states that the agent will be attracted by the opposite of its neighbor’s opinion if they share a negative link;and the repelling rule indicates that the opinions of two agents are mutually exclusive.The two parameters,αandβ,reflect the strength of positive and negative links,respectively.
Structural balance is a fundamental concept in the study of signed graphs.We say that a signed graphGis structurally balanced if there is a partition of the node set into two nonempty and mutually disjoint subsetsV=V1∪V2,where every edge between the two node subsetsV1andV2is negative,and every edge within eachViis positive,i=1,2.
Then wecan introduce the first model with the opposing rule(2.6),along with the negative links,wherexi(t)is updated as follows:
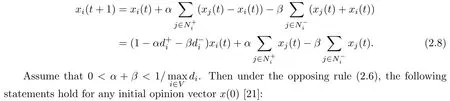
(i)IfGis structurally balanced,then
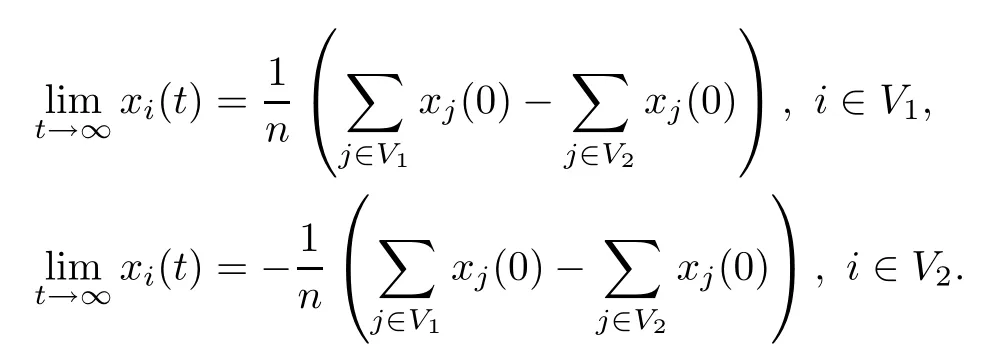
(ii)IfGis not structurally balanced,then
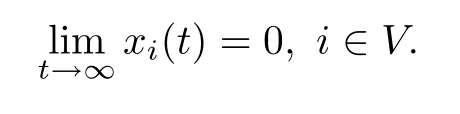
For the second model with the repelling rule(2.7),along with the negative links,xi(t)is updated as follows:

(ii)If G is not structurally balanced,then

Here,the value of(w1,···,wn)depends onαandβ.
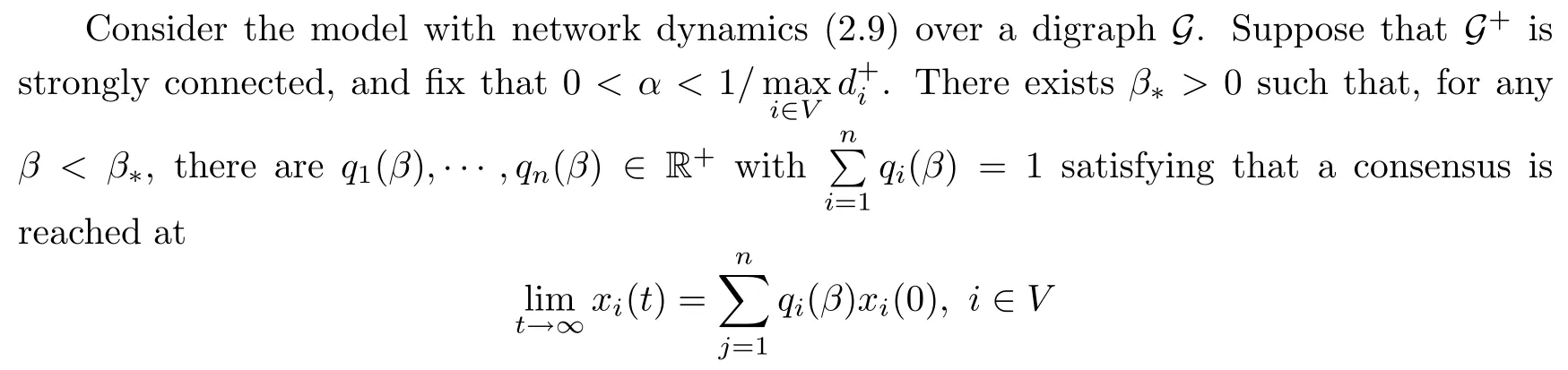
for all initial valuex(0).
We can see that different models have different properties on convergence.They can be used to describe different social phenomena.Other properties,such as rates of convergence,have also been studied.The topologies of the above models are all fixed,and can also be extended to time-varying structures.
2.4 Fashion Game
A fashion game [22–25]is essentially a deterministic 0?1 type opinion dynamics model.In this kind of social network,the value of the opinions of agents are no longer arbitrary real numbers,but binary numbers:either 0 or 1.For example,in the early 1980s,there were two kinds of trousers that were popular in some cities of China.One was straight-leg,and the other was flared.Each person’s choice of trousers was influenced by what their neighbors wore.The fashion trend of flared trousers took off at that time.When the fashion trend faded,straight-leg trousers became the dominant choice.However,in recent years,flared trousers have become popular again.Such fashion evolution is very common,and the fashion game can give a good explanation for it.
Regarding fashion,there are two viewpoints that are both extremely popular but almost opposite to each other.Some think that fashion is a distinctive or peculiar manner or way.Others take fashion to be the prevailing custom or style.People falling into the first class are called rebels,and the latter are called conformists.Since fashion comes from comparison with others,and the range of fashion from which people compare is almost always confined to their friends,relatives,colleagues,and neighbors,that fashion works through a social network is very natural [26,27].
LetG=(V,E)be a social network,whereV={1,2,···,n}is the set of agents andE?V×Vis the set of edges(no self-loops are allowed).Each agent is faced with a binary choice of opinions 0 or 1,and they can only form opinions that affect themselves through the opinions of their neighbors.Time is discrete fort=0,1,2,···and every agent has an opinion at timet,which is denoted byxi(t)for agenti.Denote the set of neighbors of playeribyNi.For agenti∈V,they are either a conformist or a rebel,and its type does not change over time.Conformists tend to take the most common views among their neighbors,while rebels tend to take the opposite.At timetall agents obtain their neighbors’opinions.If an agent’s neighbors have equal numbers of agents with opinions 0 and 1,then this agent will not change their opinion at timet+1.Otherwise,a conformist agentiwill update their opinion at timet+1 to the more selected opinion value at timetfor agents inNi,while a rebel agentjwill update their opinion at timet+1 to the less selected opinion value at timetfor agents inNj.
More precisely,giving an opinion profilex(t)=(x1(t),···,xn(t))∈{0,1}n,the utility of agentiis defined by
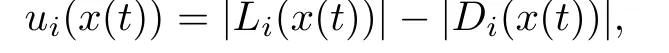
where
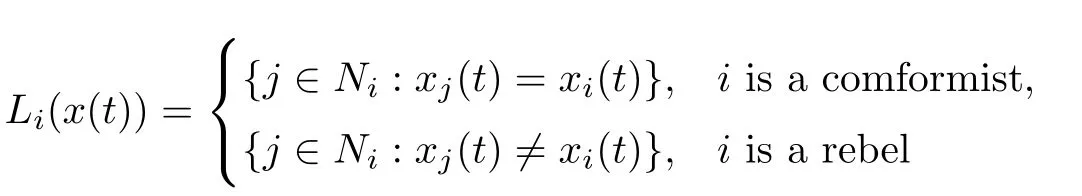
is the set of neighboring agents thatilikes,andDi(x(t))=NiLi(x(t))is theset of neighboring agents thatidislikes.Theui(x(t))can also be referred to as the satisfaction degree.Agentiis satisfied at timetifui(x(t))≥0.Otherwise,this agent is dissatisfi ed.When the agentiis dissatisfied at timet,they will change their opinion at timet+1,otherwise this agent will maintain their own opinion.Thus,these opinion values are updated synchronously according to
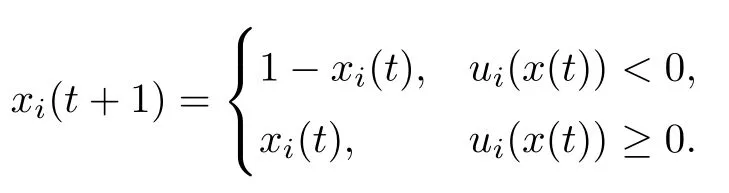
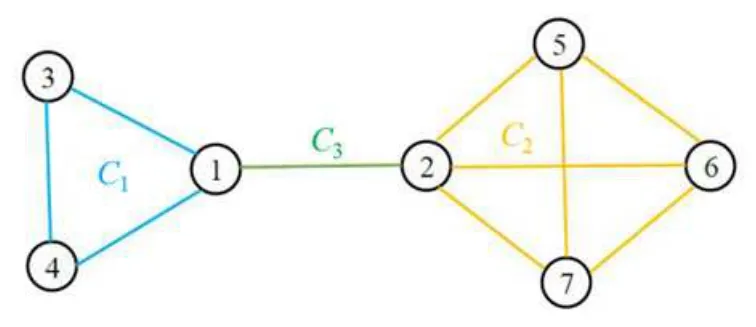
It is worth mentioning that theiterative rules of this model are inspired by matching pennies from game theory,which is why the researchers call it the fashion game.Since the network topology of the considered system is fixed,the value updating process is deterministic;the opinion vector at a specific time is only dependent on the opinion vector at the last time,and the opinion vector has only a finite number of values,i.e.,2n;the system will eventually enter a cycle,that is,at a certain momentT,x(T)=x(s)holds for some 0≤s Zhigang Cao et al.[24]introduced the homophily index to further study the fashion cycle,and concluded that a lower homophily index usually promotes the appearance of fashion cycles. Gossip algorithms can be regarded as a special kind of algorithm in social networks,and they are widely used in modern distributed systems.As the name suggests,the gossip algorithm is inspired by gossip:in an office,when a person gossips about a piece of social news,everyone in the office will know the news for a limited time.The gossip protocol,which characterizes a manner of information dissemination and aggregation on social networks,was proposed in 1987 by Alan Demers [28].For the gossip algorithm,the key indicators are the convergence and speed of the convergence of the algorithm.This section will introduce some classic gossip algorithms [29–31,39],and make certain extensions on the basis of existing algorithms. Consider a networkG=(V,E)with the node setV={1,···,n}.The value nodeiholds at timetis denoted asxi(t)∈R for discrete timet=0,1,2,···.The global network state is then given byx(t)=(x1(t),···,xn(k))T.Unlike the DeGroot model,in the deterministic gossip algorithm,only two selected agents update their values or opinions to the average of the values they held prior to the interaction at timet+1,and the values of all other agents remain unchanged.Therefore,at timet+1,the update rule for agents can be expressed as To simplify the update rule,a matrix set is introduced,whereInis then×nidentity matrix,andem=(0···0 1 0···0)Tis then×1 unit vector whosem’th component is 1. For a deterministic gossip algorithm,we have a given functionW(t)from nonnegative integers toMn.Then the update rule can be expressed in the following matrix form: We can see that this has the same matrix form as the DeGroot model.The same method can be used to analyze the speed of convergence. It is straightforward to ask the question of whether the deterministic gossip algorithm is convergent in finite time.More precisely,we say that algorithm(3.1)achieves finite-time convergence with respect to initial valuex(0)∈Rnif there exists an integerT(x0)≥0 such thatx(T)=WT?1···W0x(0)∈span {1},and global finite-time convergence if suchT(x0)≥0 exists for every initial valuex(0)∈Rn.Here1is the vector with all entries being 1. There exists a deterministic gossip algorithm that converges globally in finite time if and only if the number of network nodes is a power of two.Forn=2mnodes,the fastest gossip algorithms take a total ofmn=nlog2nnode updates to converge.Moreover,if there exists no integerm≥0 such thatn=2m,then,for almost all initial values,there exists no deterministic gossip algorithm with finite-time convergence. For deterministic gossip algorithms,if only one of the two selected interacting agents updates their opinion,we say it an asymmetric deterministic Gossip algorithm.The model description of the asymmetric deterministic gossip algorithm and the conclusion of finite time convergence can be found in [30]. We can see that in the above subsection,the value ofW(t)is a prefixed matrix.This can be extended to randomized algorithms;that is,W(t)is not a matrix but a distribution onMn. We consider a special case as an example.At any time,an agent is selected at random and then this agent selects one of their neighbors randomly to communicate.We can use a nonnegative random matrixP=(pij)∈Rn×nto characterize this kind of randomized gossip algorithm.Herepij>0 if and only if {i,j}∈E,and a random matrix is a matrix in which the sum of any row elements is 1.Furthermore,we assume that the biggest eigenvalue ofPis 1,and the absolute value of all othern?1 eigenvalues are less than 1.The randomized gossip algorithm relevant toPcan be described as follows:at timet,agentiis selected randomly with probability,and then agentjas one of agenti’s neighbor is selected with probabilitypij.Then,agentiandjboth update their opinion values to their average value,i.e., Letx(t)be the opinion vector at timetfor all agents.The updating rule can be described as whereM(t)is a random variable which is It is easy to see that whereρ(A)represent the largest absolute value of eigenvalues of the matrixA. When we get the convergence of the algorithm,it is more valuable to study the speed of convergence.Boyd [29]introduced the concept of?-average time:for any 0 where‖·‖is thel2norm.Intuitively,?-average time describes the shortest time needed forx(t)reach to the?neighborhood ofxave1with high probability,regardless of the initial valuex(0). Theorem [29]shows that In this subsection,we introduce the randomized boolean gossip model [31].Like fashion games,every agent holds binary values 0 or 1.However randomized boolean gossip models are random algorithms,just as their names indicate,while fashion games are deterministic.Moreover,the evolution of opinions is based on boolean logic. Also,we consider a social networkG=(V,E)withnagentsV={1,2,···,n}.There is no self-loop inE,andGis connected.Time is discrete liket=0,1,2,···.At any moment,agentiholds a binary opinionxi(t).At every time,a pair of agents,iandj,are randomly selected such that {i,j}∈E.They update their opinion according to a boolean function on their opinions.Note that there are 16 boolean functions that map {0,1}2into {0,1}.We use that⊙kspecifies a binary boolean function and thata⊙kbrepresents the value of⊙k(a,b).The set of all 16 boolean functions is denoted byH. LetC?be a subset ofHwhich specifi es all possible updating rules between two nodes.Assume thatCcontainsqelements.ThenCcan be represented by As the setCcan be arbitrary subsets of the set of all boolean functioinsH,this randomized boolean gossip model not only can be used to analyze the evolution of social opinions [32],but also can be used to explain gene regulation [33]and virus spreading [34]. Letx(t)=(x1(t),x2(t),···,xn(t)),t=0,1,···denote the stochastic process determined by the above model.This process defines a Markov chain with 2nstates,MG(C)=(Sn,P),where Next,we consider a special case.The setCdoes not involve the negation rule?,and we use the conventional notation∧to represent that boolean“AND”operation and∨to represent“OR”operation.We term such types of boolean operations as positive boolean dynamics,and define thatCpst={∨,∧}.For this kind of randomized boolean gossip model,the Markov chain is an absorbing chain with two absorbing states,[0···0]and [1···1].Thus,from the standard theory of Markov chains,forx0=x(0)∈Sn{[0···0],[1···1]},we can find a Bernoulli random variablex?,such that For other binary valued opinion dynamics,Yildiz [35]studied models with stubborn agents who never change their opinions. Cliques are complete subgraphs and are very common in social,computer,and engineering networks.They have been applied to beamforming and clustering in wireless sensor networks [36,37]and quantum networks [38].Yang Liu et al.[39]introduced the concept of cliques in gossip algorithms to speed up the gossip algorithms.Intuitively,in clique gossip algorithms,all of the agents in the clique update their opinions simultaneously,while in gossip algorithms,only one pair of agents updates their opinions. We see that the updating rule can be represented by matrix forms If all agents in the clique update their opinions as their average opinion in the clique,the updating rule is Just as randomized gossip algorithms,the above updating rule can be randomized.Ifσ(t)is prefixed,this algorithm is deterministic.Ifσ(t)is a distribution onH?G,then this is a randomized clique gossip algorithm. The finite time convergence was considered.One can find anm-regular clique coveragewhich leads to a globally finite-time convergent clique gossip averaging algorithm if and only ifnis divisible bymwith the same prime factors asm. For randomized clique gossip algorithms,M(t)has the value with probabilitypl,l=1,2,···,d.Here Using the same method as for the randomized gossip algorithms,we have so the convergence of these algorithms is still determined by We can defineTave(?)as?-average time of a convergent randomized clique gossip algorithm as and we also know that it satisfies that This shows that the second largest eigenvalue ofMdetermines the speed of the convergence. Although the aim of introducing cliques gossip algorithms is to boost the speed of the algorithms,an interesting phenomenon shows that the involvement of cliques does not always accelerate the computation.For complete graphs,the introduction of regular cliques does improve the performance of the algorithms.The following example shows that the second largest eigenvalue may be less than the one in the relevant randomized gossip algorithm. Consider the social networkG(V,E)as shows in the figure,whereV={1,···,7}.The clique coverage is={C1,C2,C3},where three cliques have different sizes. Figure 1 Social networks with 7 agents For the randomized gossip algorithm,one of the 10 edges is selected with equal probability at timet.The two agents of this edge communicate and update their opinions as the average opinion.We can obtain that=0.980084. For the randomized clique gossip algorithm,one of the three cliques is selected at timetrandomly.The cliquesC1,C2,andC3are going to be selected with probabilitiesp,q,and 1?p?q,respectively.All of the agents of the selected clique communicate and update their opinions as the average opinion of the clique.Then, We see that in this social network,the speed of convergence of clique gossip algorithms is relevant to the probability of the cliques being chosen.Under differentpandq,we cannot be assured that randomized clique gossip algorithms are faster than randomized gossip algorithms. Whether it is the classic social network model or the above-mentioned Gossip algorithm,agent opinion values are one-dimensional real values,so there exists an order relationship.However,some real-life instances,such as the well-known rock-paper-scissors game,do not have an order relationship.They can no longer be described by one-dimensional real values.As another example,some people like to go out for activities at three o’clock in the afternoon every day,while others go at five o’clock.The value range of these time points is a circle on the clock.Inspired by this,we take agent opinion values from the unit circle and study the consensus of agent opinions. Consider a social networkG=(V,E)consisting ofnagents.Time is slotted and the value that agentiholds at timetis denoted byvi(t)=(xi(t),yi(t))∈R2,whereIt is not difficult to find that for any agentiand timet,there is a unique angleθi(t)∈[0,2π)such thatxi(t)=cosθi(t),yi(t)=sinθi(t).That is,we can useθi(t)to characterize the opinion vectorvi(t)of agenti. Since,for anyr∈R,there is a uniqueθ∈[0,2π)such thatis an integer,we introduce the notation mod(r)to representθ. The evolution of opinions still proceeds in a random gossip manner,that is,at timet,agentiis randomly selected fromV,and agentjis randomly selected fromi’s neighbor setNito communicate withi.We also use averages to update the opinions ofiandj.How do we take the average on the circle?We know that any two points on the unit circle will divide the circumference into two arcs:when the two arcs are equal in length,they are both semicircles;otherwise,the arc larger than the semicircle is the superior arc,and the arc smaller than the semicircle is the inferior arc.The midpoint of both arcs can be called the average of the two viewpoints.Of course,because the distance between the inferior arcs is closer,we think that individuals are more likely to shift their opinions to the midpoint of the inferior arc after communication,and less likely to shift their opinion to the midpoint of the superior arc.Furthermore,if the opinions of these two agents are the same,their opinions should be the same after the communication.We can borrow a model from quantum networks [40]to define the updates of agentiand agentjas follows:agentiand agentjindependently update their opinions to TheoremAll the nodes reaches consensus almost surely,i.e., where‖·‖is thel2norm in R2. ProofLetpijbe the probability that agentiand agentjare chosen at any specific time.Denote that where It is easy to verify that Moreover, Therefore,we can conclude that The inequality(3.2)implies thatg(t)is a submartingale.It is easy to verify that for allt,g(t)≤n2.Therefore,according to the Martingale Convergence Theorem,g(t)converges to a finite limit with probability 1.LetGrepresent the limits ofg(t).In other words, By Inequality(3.2)and the Dominated Convergent Theorem,we can prove that Thus,for any {k,l}∈E, In this paper,we introduced a few types of models of social networks.The key differences among these models can be characterized as follows: (1)The manner of communication between agents.In the DeGroot model,the signed social network models,and fashion games,agents communicate with all their neighbors.In the Krause model,agents only communicate with neighbors whose opinions do not deviate too much from their own.In gossip algorithms,agents just choose one neighbor with whom to communicate,while in clique gossip algorithms,agents choose all neighbors in one clique with which to communicate. (2)The set of all possible opinions.In fashion games and randomized boolean gossip algorithms,the possible values of opinions are just 0 and 1.For other models,the possible set is the real numbers.In the last subsection,we introduced the unit circle as the possible set for the first time. (3)Consists of Deterministic or randomized. (4)The network topology.The underlying graph can be directed,undirected,or even signed.Moreover,the network topology can be time-variant or time-invariant. Different combinations of these characteristics form different models,which can then be used to describe different social network phenomena.Opinion dynamics is an interdisciplinary field that has implications for economics,computer science,biology,and mathematics.The technical tools used for studying these models come from graph theory,matrix analysis,combinatorics,probability,and even artificial intelligence.It is a thriving field that deserves a wider attention.3 Gossip Algorithms
3.1 Deterministic Gossip Algorithms

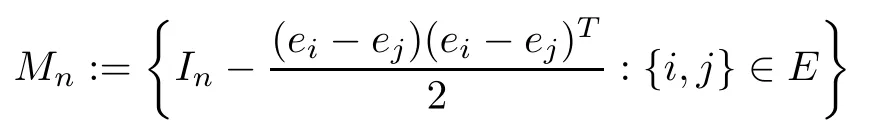
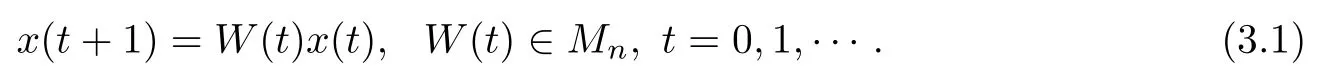
3.2 Randomized Gossip Algorithms
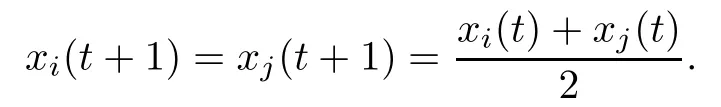
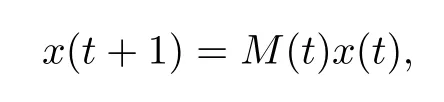
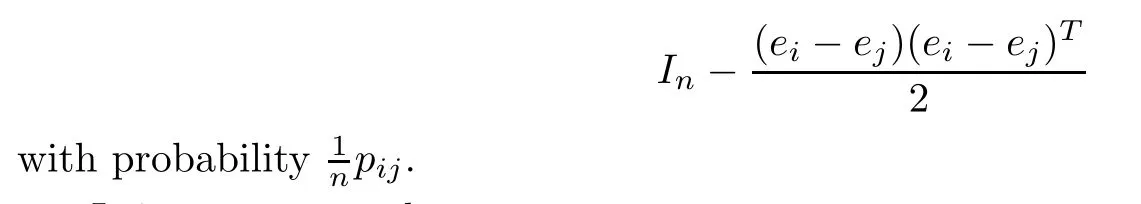


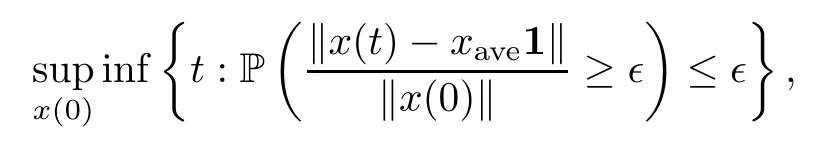
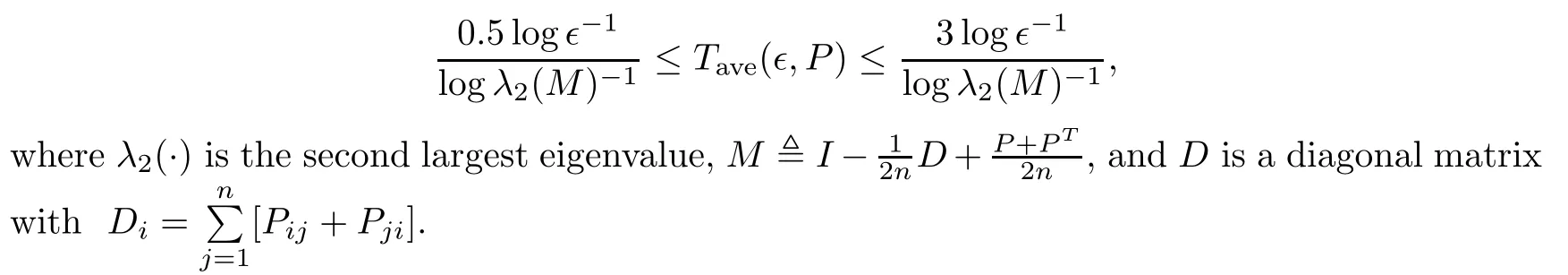
3.3 Rand omized Boolean Gossip Model


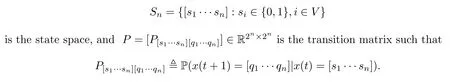
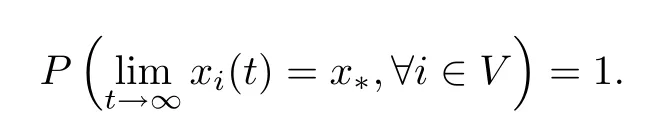
3.4 Clique Gossip Algorithms



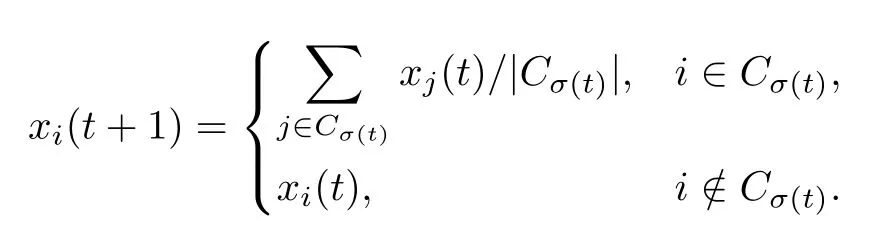
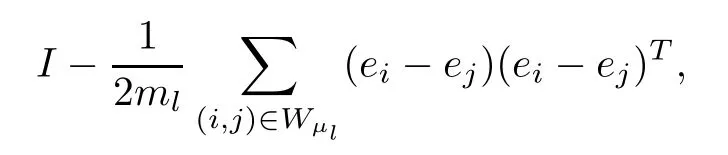
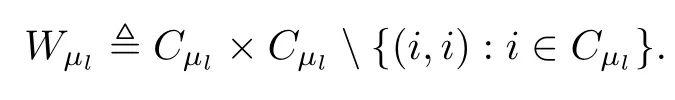
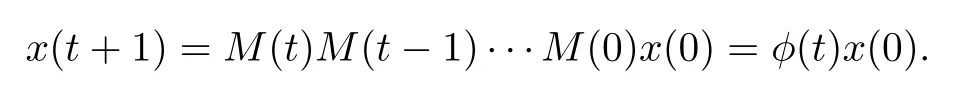
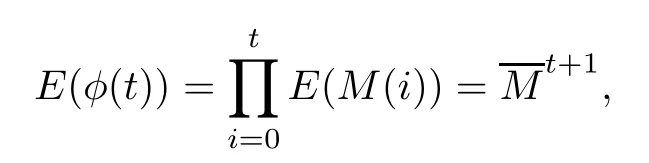

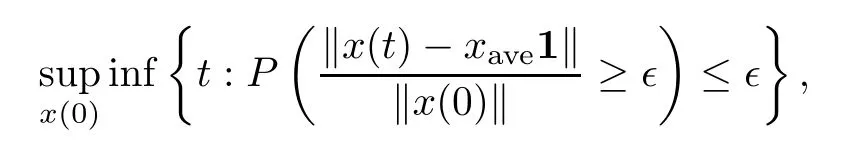
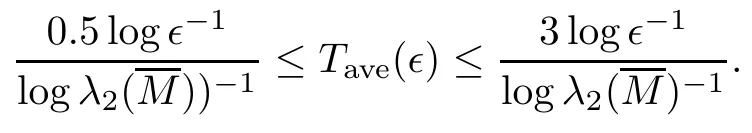
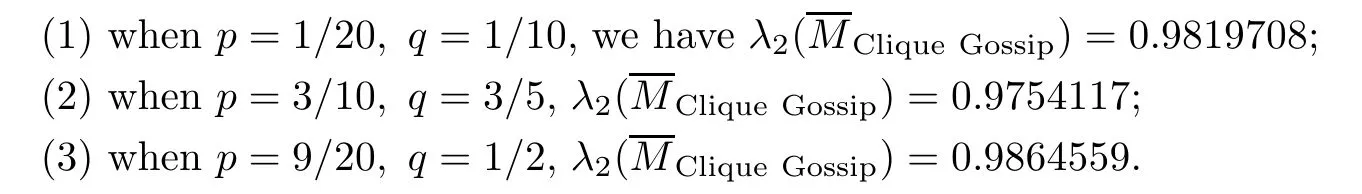
3.5 Randomized Gossip Algorithm on the Unit Circle




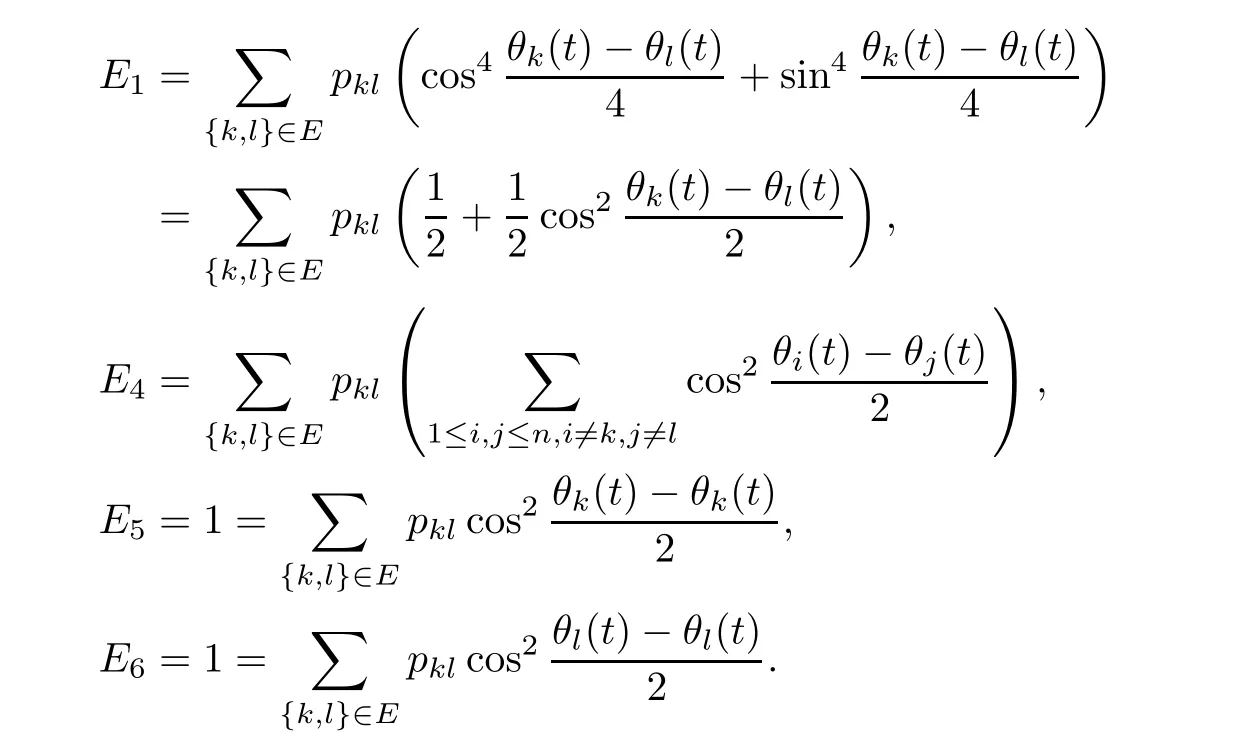
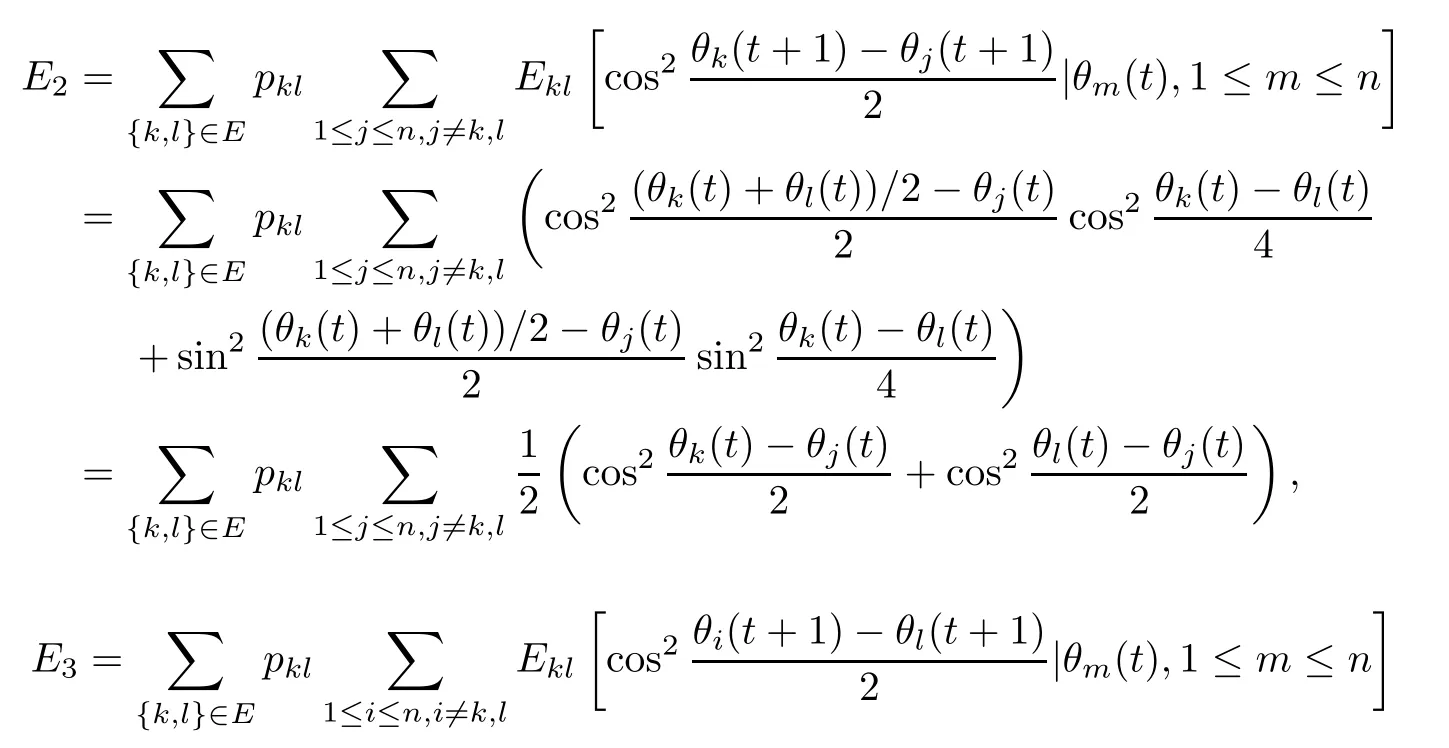
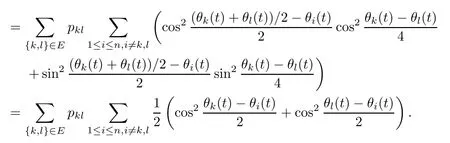
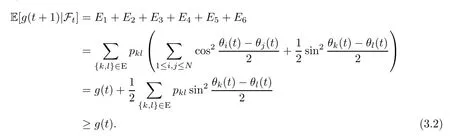
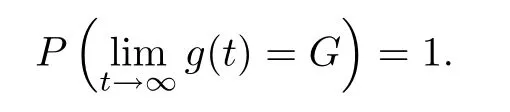
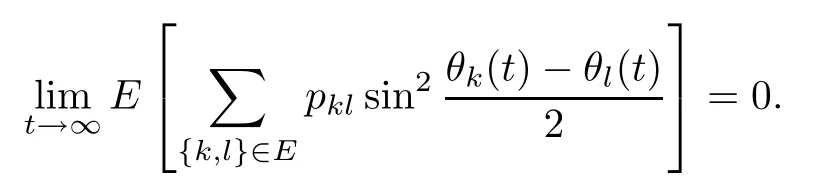

4 Conclusion
 Acta Mathematica Scientia(English Series)2022年6期
Acta Mathematica Scientia(English Series)2022年6期
- Acta Mathematica Scientia(English Series)的其它文章
- L 2-CONVERGENCE TO NONLINEAR DIFFUSION WAVES FOR EULER EQUATIONS WITH TIME-DEPENDENT DAMPING?
- MONOTONICITY FORMULAS FOR PARABOLIC FREE BOUNDARY PROBLEMS ON CONES?
- ON THE(CO)HOMOLOGY OF(QUOTIENTS OF)MOMENT-ANGLE MANIFOLDS OVER POLYGONS?
- ISOPARAMETRIC HYPERSURFACES AND COMPLEX STRUCTURES?
- A NONLINEAR SCHR?DINGER EQUATION WITH COULOMB POTENTIAL?
- THE MINIMAL GENUS PROBLEM—A QUARTER CENTURY OF PROGRESS?
