Ruifeng QIU()Yanqing ZOU()

School of Mathematical Sciences&Shanghai Key Laboratory of PMMP East China Normal University,Shanghai 200241,China

E-mail:rfqiu@math.ecnu.edu.cn;yqzou@math.ecnu.edu.cn

Abstract A Heegaard splitting is a type of combinatorial structure on an orientable compact 3-manifold.We will give a survey on Heegaard spliting and its applications,including those pertaining to the classifi cation and stabilization problem,reducibilities,minimal Heegaard splitting and Heegaard distance.

Key words stabilization;Heegaard genus;Heegaard distance

Dedicated to Professor Banghe LI on the occasion of his 80th birthday

1 Introduction

A compact orientable 3-manifoldHis a handlebody if it is obtained from attaching finitely many 1-handles on a 3-ball.The genus of a handlebody is the genus of its boundary surface.In 1898,Heegaard [22]introduced a splitting for a closed,orientable and triangulated 3-manifoldM.Namely,assume thatS?Mis a closed,orientable surface.CuttingMalongSproduces two handlebodies,H1andH2,with the same genera.ThenH1∪SH2is called a Heegaard splitting ofM.In the1950s,Moise and Bing [5,56]proved that any closed orientable3-manifold admitsa triangulation.Therefore,any closed orientable3-manifold admitsa Heegaard splitting.Later,Haken [19]introduced a compression bodyVand defined a Heegaard splitting for a compact orientable 3-manifold.Hence,any compact orientable 3-manifold admits a Heegaard splitting.

Heegaard splitting is widely studied from many perspectives,including with regard to the classification and stabilization problem,the minimal Heegaaard splitting problem and Heegaard distance and its relation to the topology and geometry of 3-manifolds.

2 Classification and Stabilization Problem

A key fact is that any two once stabiliztions of a Heegaard splitting are isotopic.This raises the question:is there a common stabilization for two non-isotopic Heegaard splittings of a 3-manifold?Pertaining to this question,Reidemeister and Singer [66,84]proved the following theorem;see also in Lei [40]and Johnson [28]:

Theorem 2.1(Common stabilization)For any two Heegaard splittings ofM,there is a Heegaard spliting as their common stabilizations.

Another question is:for any two Heegaard splittings of a 3-manifold,how many stabilizations needed to get a commmon stabilization?Rubinstein-Scharlemann [67,68]proved

Theorem 2.2(1)For any two strongly irreducible Heegaard splittings of a 3-manifold,suppose one has genuspwhile the other has genusq,p≥q.Then there is a genus 8q+5p?9 Heegaard splitting as their common stabilization;

(2)For any two Heegaard splittings of a non Haken 3-manifold,suppose that one has genuspwhile the other has genusq,p≥q.Then there is a genus 8q+5p?9 Heegaard splitting as their common stabilizations.

In their proof of the above,Rubinstein-Scharlmann studied sweepouts for these two Heegaard splittings and defined the Rubinstein-Scharlemann graphic.Kobayashi-Saeki [38]described this graphic as the discriminant set of a stable map from a 3-manifold to a plane.On this,the discriminant set is the image of the singular set under the stable map.In [28],Johnson looked at two Morse functions with respect to these two Heegaard splittings,and defined a similar graphic,which is the discriminant set of a stable function onM.

For any two Heegaard splittings of a Seifert fibered space,Schultens [80]proved that there is a common stabilization which is a single stabilization of the larger genus one.For more such cases,see Sedgewick [83].The question of whether a single stabilization is sufficient is called the stabilization conjecture;see Kirby [32].

Conjecture 2.3(Stabilization conjecture)For any two Heegaard splittings of a 3-manifold,a single stabilization of the larger genus Heegaard splitting is a common stabilization of them.

Unfortunately,this conjecture is not true in general.Hass-Thompson-Thurston [24]proved

Theorem 2.4For anyg>1,there is a 3-manifoldMgwith two genusgHeegaard splittings that requiregstabilizations to become equivalent.

After that,Johnson [29]and Bachman [3]also gave some counterexamples to the Stabilization conjecture.

It is known that doing stabilizations produces many more non-isotopic Heegard splittings for a 3-manifoldM.Thus,if we want to give a classfi cation of all Heegaard splittings ofM,we only consider unstabilized Heegaard splittings.One magnifi cent result proved by Waldhausen [89]is as follows:

Theorem 2.5Any genus of at least one Heegaard splitting ofS3is stabilized.

For Lens space,Bonahon-Otal [6,7]proved that there is only one unstabilized Heegaard.We say that a 3-manifoldMis reducible if there is an embedding 2-sphere so that it bounds no 3-ball inM.Kneser-Milnor [31,53]introduced the following famous and beautiful theorem,which is the fundamental theorem in 3-manifold theory.

Theorem 2.6(Primedecompostion theorem)Every orientable compact 3-manifold is the connected sum of finitely many irreducible 3-manifolds and finitely manyS2×S1.Moreover this decomposition is unique up to some permutations.

Before stating more results on Heegaard splitting,we introduce the definition of a reducible Heegaard splitting.

Definition 2.7is reducible if there is an essential simple closed curvec?Sso that it bounds a disk on either side ofS.Otherwise,it is irreducible.

For a reducible 3-manifold,Haken [19]proved the following famous lemma:

Theorem 2.8(Haken’s Lemma)Every Heegaard splitting of a reducible 3-manifold is reducible.

IfMis reducible,i.e.,M=M1#M2,by Haken’s Lemma,every unstabilized Heegaard splitting is a connected sum of two unstabilized Heegaard splittings ofM1andM2.Conversely,there is a natural question that arises:is the connected sum of any two unstabilized Heegaard splittings ofM1andM2unstabilized?Gordon [32]introduced the following conjecture(it was proved by Qiu-Scharlemann [63]and Bachmann [2]independently):

Theorem 2.9(Gordon’s conjecture)The connected sum of two Heegaard splittings is stabilized if and only if at least one of these two Heegaard splittings is stabilized.

By this result,for studying unstabilized Heegaard splittings of a compact orientable 3-manifold,it is sufficient to study all unstabilized Heegaard splttings ofS2×S1and an irreducible 3-manifold.Since Heegaard splittings ofS2×S1are well studied,we only consider unstabilized Heegaard splittings of an irreducible 3-manifold.Boileau-Otal [8]proved that there is a unique genus three Heegaard splitting forT3.In their proof,the crucial step is to prove that each Heegaard splitting is either a stabilization of the unique genus one Heegaard splitting or a stabilization of the unique genus two Heegaard splitting,which we call the standard Heegaard splitting.Scharlemann-Thompson [72]showed that each Heegaard splitting of a product I-bundle of a closed surface is standard;see Schultens [79]for a closed surface overS1.Moriah-Schultens [54]proved that all irreducible Heegaard splitting of a Seifert fibered space are either vertical or horizontac.Then,Rubinstein-Scharlemann [69]gave a classifi cation of all genus two Heegaard splittings.On the opposite side,Casson-Gordon [10]and Kobayashi [33]constructed an irreducible 3-manifold which has infinitely many non-isotopic unstabilized Heegaard splittings.Waldhausen [90]then introduced the following conjecture:

Conjecture 2.10(Waldhausen conjecture)For any close,irreducible and orientable 3-manifoldMandg,if it is atoroidal,there are at most finitely many non-isotopic and genusgHeegaard splittings.

Using essential lamination theory,Li [41,42]proved this conjecture,while Johanson [26,27]proved the original version.More precisely,Li proved

Theorem 2.11(1)IfMcontains no incompressible torus,then there are at most finitely many non-isotopic and genusgHeegaard splittings.

(2)IfMis a non-Haken 3-manifold,then it admits finitely many non-isotopic Heegaard splitting.

Recently,Colding-Gabai-Ketover [11]listed all those possible Heegaard splittings for a non-Haken 3-manifold.

NoteThere is an example showing that ifMcontains an incompressible torus,then it admits infinitely many non-isotopic but same genus Heegaard splittings.

3 Reducibilities of Heegaard splittings

From now on,we assume thatMis a compact,irreducible and orientable 3-manifold.

Definition 3.1 A properly embedded surfaceF?Mis incompressible ifFis neither a 2-sphere nor a disk,andiπ:π1F→π1Mis injective.

Jaco,Shalen and Johanson introduced the JSJ decomposition forM.After that,Thurston [87]introduced the famous Geometrisation conjecture(proved by Thurston and Perelman):for any closed orientable 3-manifoldM,there are finitely many incompressible tori {T1,···,Tn}so that each component ofis either a Seifert fibered space,a solvable 3-manifold,or a hyperbolic 3-manifold.

An irreducible and orientable 3-manifold is a Haken 3-manifold if it contains an embedded closed orientable incompressible surfaceF.Waldhausen [88]proved that Haken 3-manifolds are determined by their fundermantal group.In general,there are many more Haken 3-manifold.Thurston [87]proposed the virtually Haken conjecture,proven by Agol [1]as follows:

Theorem 3.2(Virtually Haken conjecure)Any hyperbolic 3-manifold has a Haken 3-manifold as its finite covering.

As indicated by Kneser-Milnor’sprime decompostion theorem and Thurston’s Geometrisation conjecture,there are many rich combinatorial structures in Heegaard splitting.Letbe a Heegaard splitting ofM.It is not hard to see that ifis reducible,then it is stabilized.Therefore,it is essential to study all irreducible Heegaard splittings ofM.Casson-Gordon [10]introduced a weakly reducible Heegaard splitting.

Futher more,they proved

Theorem 3.4IfMadmits a weakly reducible and irreducible Heegaard splitting,then it contains a closed incompressible and orientable surface.

Remark 3.5Casson-Gordon’s theorem was a landmark result in Heegaard splitting.Moreover,their theorem and the Scharlemn-Thompson thin position theorem below are two basic tools for studying Heegaard splitting.

Using thin position theory,Scharlemann-Thompson [71,73]defined an untelescoping for a weakly reducible and irreducible Heegaard splitting,usually called a generalized Heegaard splitting,as follows:

Theorem 3.6There are finitely many disjoint and non-isotopic closed incompressible surfaces {F1,···,Fn}inMso thatis an amalgamation of finitely many strongly irreducible Heegaard splittings,i.e.,

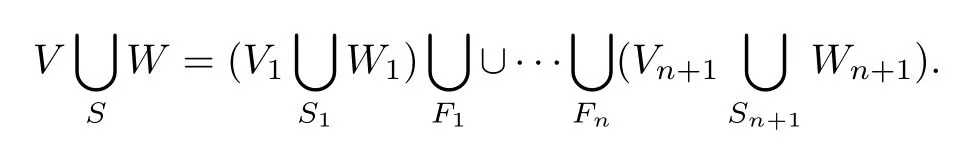
4 Heegaard Distance

LetSbe a closed,orientable surface with a genus at least two.Harvey [20]defined the curve complex C(S)as follows:

(1)Vertices:isotopic classes of essential simple closed curvesCinS;

(2)K-simplex:a collection ofK+1 vertices so that they are pairwise disjoint and nonisotopic.Then C(S)isa 3g?4 dimensional simplicial complex.Though it isnot locally compact,Masur and Minsky [49,50]defined a distancedon C1(S).Under this distance,for any two verticesα,β∈C(S),

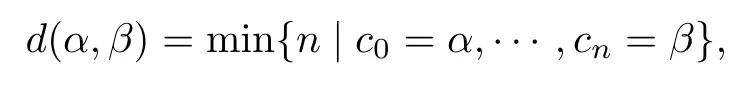
where eachciis a vertex andci∩ci+1=?for 0≤i≤n?1.With definition of curve complex,for a Heegaard splittingHempel [23]defined the Heegaard distanced(V,W)=min {d(α,β)|α(resp.β)bounds a disk inV(resp.W).}

One fundamental problem is constructing given distance Heegaard splittings.Hempel [23],Minsky-Moriah-Schleimer [51]proved that there are arbitrary large distance Heegaard splittings.With tools from curve complex,Guo,Qiu,Zhang and Zou [64,93]proved the following theorem(see also in Ido-Jang-Kobayashi [25]):

Theorem 4.1For anyg≥2,d≥1 except(g,d)=(2,1),there are infinitely many nonhomeomorphic 3-manifolds admitting distancedand genusgHeegaard splittings.Moreover,if(g,d)(3,1),then all of these 3-manifolds are hyperbolic.

NoteBy definition,there is no genus 2 and distance 1 Heegaard splitting.If(g,d)=(3,1),then a distance 1 and genus 3 Heegaard splitting is weakly reducible and hence,by Scharlemann-Thompson’s thin position theorem,it contains an incompressible torus and will not be hyperbolic.

In their construction,Guo,Qiu,Zhang and Zou carefully chose a hand lebody without reducing the Heegaard distance.If we can find out all distance reducing or distance degenerate handle additions,then we have more liberty to construct 3-manifolds with special properties.Before stating some results,we introduce the definition of a distancedegeneratehandleaddition.

Theorem 4.2(Finite Diameter Ball)For any distance of at least 3 Heegaard splittings,all of those distance degenerate curves lie in a diameter finite ball in a curve complex of the boundary surface.

NoteFor a distance 2 Heegaard splitting of a torus I-bundle,each Dehn filling produces a solid torus.Since each Heegaard splitting of a solid torus is at most 1,each Dehn filling of a torus I-bundle is distance degenerate.

By the definition of Heegaard distance,a reducible Heegaard splitting has distance 0;a weakly reducible Heegaard splitting has a distance of at most 1;a strongly irreducible Heegaard splitting has a distance of at least 2.This means that every Heegaard distance of a reducible 3-manifold is 0.For any toroidal or annular 3-manifold,Hempel [23]first proved.

Theorem 4.3IfMcontains an essential torus or annulus,then every Heegaard distance is at most 2.

An properly embedded surfaceF?Misessential ifFisincompressibleand isnot contained in an I-bundle of?M.In general,Hartshorn [21]and Scharlemann [70]proved

Theorem 4.4For any essential surfaceF?M,every Heegaard distance is bounded by 2?χ(F).

NoteHartshorn proved the casein whichFis closed and incompressiblebut not boundary parallel to?M.Then Scharlemann proved the general case in whichFis an essential surface inM.

Not only Heegaard distance bounds essential surfaces,but there is also a strong relation based on Heegaard distance,between two Heegaard splittings of the same 3-manifold.Before stating some results,we introduce a definition.

Definition 4.5A closed orientableF?Mis strongly irreducible if

?Fis separated inM;

?Fis compressible from its two sides;

?for any pair of compression disks,DandE,from two sides,?Dintersects?Enontrivially.

Scharlemann-Tomova [76]proved

Theorem 4.6Letbe a Heegaard splitting ofMand letF?Mbe a strongly irreducible surface.Then

?eitherFlies in a product I-bundle of?M;

?Fis isotopic toS;

?d(S)≤2?χ(F).

NoteLi [44]gave a simplified version of Scharlemann-Tomova’s proof.

In particular,for any strongly irreducible Heegaard surfaceS,by Theorem 4.6,each Heegaard surface ofMis either isotopic toSor has distance of at most 2g(S).It means that if a Heegaard splitting has large enough distance,then it is the unique mininal Heegaard splitting.

Remark 4.7Usually it is hard to construct a 3-manifold so that it contains no small genus incompressible surface or strongly irreducible surface.Nevertheless,by Theorems 4.4 and 4.6,we can construct such 3-manifolds by constructing high distance Heegaard splittings.This is one reason that Heegaard distance has led to some important advances in Heegaard splitting.

With Thurston’s geometrisation conjecture,Hempel [23]proved that a distance of at least 3 Heegaard splittings corresponds to a hyperbolic 3-manifold.By Theorem 4.1,it is possible that a distance at most 2 Heegaard splitting corresponds to a hyperbolic 3-manifold.Now,comes a problem.

Problem 4.8Determining the geometry of distance of at most 2 Heegaard splittings.

By introducing a locally large Heegaard splitting,Qiu and Zou [65]gavean explicit geometry of a locally large distance 2 Heegaard splitting.The further question is

Question 4.9How to describe the geometry of a distance 2 but locally small Heegaard splitting?

Let Mod(S)=Homeo+(S)/isotopy be the mapping class group ofS.Similarly,for a compression bodyV,Mod(V)=Homeo+(V)/isotopy is the mapping class group ofV.It is known that Mod(V)is a proper subgroup of Mod(S).One interesting question is:when does an element of Mod(S)extend toV?To the best of our knowledge,there is no answer to this question.For a Heegaard splittinglet Mod(S:V,W)be subgroup of Mod(S)extending to bothVandW.Minsky [17]proposed the following question:

Question 4.10Is Mod(S:V,W)finite,finitely generated,or finitely presented?

On the one hand,if its Heegaard distance is at most 1,then Mod(S:V,W)is infinite.On the other hand,Johnson [30],Namazi [59]proved that if the Heegaard splitting has a distance of at least 4,then Mod(S:V,W)is finite.Later,Qiu-Zou [94]proved that if the Heegaard splitting has a locally large distance of at least 2,then Mod(S:V,W)is finite.Thus the interesting question is:what about distance 2 or 3 Heegaard splittings?For the finite presentation problem,Cho-Koda [13]proved that,for any genus 2 reducible Heegaard splitting,the mapping class group is finitely presented.

Remark 4.11In Johnson and Namazi’s results,the 3-manifold is hyperbolic and hence its mapping class group is finite(a well known result in hyperbolic 3-manifolds).However,in Qiu-Zou’s result,there is a JSJ length 2 non-hyperbolic 3-manifold which has a finite mapping class group.This means that the finiteness problem for mapping class groups of 3-manifolds is not as simple as we hoped.

5 Minimal Heegaard Splittings of Haken 3-Manifolds

Question 5.1When is an amalgamation of two minimal Heegaard splittings minimal;i.e.,g(M)=g(M1)+g(M2)?g(F)?

Theorem 5.2Assume that neitherM1norM2is product I-bundle of a compact surface,and that?Mi?Fis incompressible fori=1,2.If the gluing map is complicated enough,theng(M)=g(M1)+g(M2)?g(F).

Remark 5.3Lackenby [39]first proved that the equation holds if bothM1andM2are simple and the gluing mapf:F→Fis complicated.Moreover,the idea in Theorem 5.2 leads to Li’s counterexample 6.3 for the rank and genus conjecture.

Considering the complexity of these two 3-manifolds,Kobayashi-Qiu [36]proved:

Theorem 5.4If both of these two Heegaard splittings have high distances,theng(M)=g(M1)+g(M2)?g(F).

Later,the upper bound on high distance was improved by Du-Gao [14]and Yang-Lei [92].Since a distance 3 Heegaard splitting means a simple 3-manifold,following Li’s result,we may ask the following question:

Question 5.5If the high distance condition in Kobayashi-Qiu’s theorem is reduced to a distance of at least 3 one,doesg(M)=g(M1)+g(M2)?g(F)still hold?

6 Rank vs Genus Problem

By the van Kamp theorem,the fundamental group of a 3-manifold has a balanced presentation,i.e.,the same numbers of generators and relations as obtained from a Heegaard splitting.Then,forM,r(M)≤g(M).It would be interesting to know whetherr(M)=g(M).Waldhausen [90]introduced the following conjecture:

Conjecture 6.1(rank versus genus conjecture)r(M)=g(M).

Once conjecture 6.1 is true,the Poincar′e conjecture holds automatically.On the one hand,Souto [85]proved that Conjecture 6.1 is true for a mapping torus where the monodromy maybe a high power of pseudo-anosov map.Namazi and Souto [60]proved that for a generic Heegaard splitting,Conjecture 6.1 is true.On the other hand,Boileau and Zieschang [9]constructed a counterexample as follows:

Counterexample 6.2There areinfinitely many genus3 but rank 2 Seifert fibered spaces.

Later,Schultens-Weideman [82]built a graph manifold counterexample for conjecture 6.1.For the hyperblic counterexample,Li [45]proved:

Counterexample 6.3For any integern,there is a hyperbolic 3-manifoldMnso that(g(Mn)?r(Mn))≥n.

In Li’s construction of hyperbolic counterexamples,all of the minimal Heegaard splittings are weakly reducible,and hence have a distance of 1.Then it is natural to ask

Question 6.4IfMhas a distance of at least 3 minimal Heegaard splitting,doesg(M)=r(M)still hold?

7 Tunnel Numbers of Knots and Its Appliations

LetK?S3be a knot and letE(K)be its complement.Then the tunnel numbert(K)is defined asg(E(K))?1.For any two knotsK1andK2,there is a connected sum denoted byK1#K2.It is not hard to see thatt(K1#K2)≤t(K1)+t(K2)+1.Thus there arises the natural question:ist(K1#K2)≥t(K1)+t(K2)+1?This question is also called the super additivity problem of tunnel numbers under connected sum.

Norwood [62]first proved that tunnel number oneknotsareprime.In general,Scharlemann-Schultens [74,75]proved:

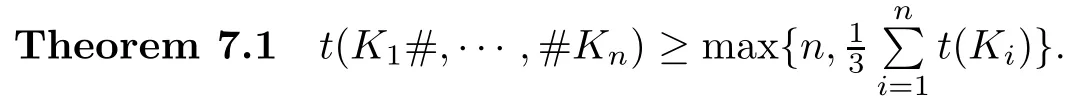
Morimoto [57]first showed thatt(K1#K2)=t(K1)+t(K2)+1 does not always hold.Kobayashi [34]gave an examplethatt(K1#K2)≤t(K1)+t(K2)?nfor any integern.However,if wemakesome restrictions on knots,the equation thatt(K1#K2)≤t(K1)+t(K2)+1 is likely to be true.We say that a knotKis small ifE(K)contains no closed incompressible surface which is not boundary parallel to?E(K).For example,Schultens [81]proved:

Theorem 7.2If both of these two knots are small,thent(K1#K2)≥t(K1)+t(K2).

Morimoto [58]introdued the definition ofg1(K)for a knotK,which is the minimal Heegaard genus ofS3,so thatKintersects each handlebody in one trivial arc system.They furthermore proved:

Theorem 7.3If bothK1andK2are meridionally small,thent(K1#K2)=t(K1)+t(K2)+1 if and only ifg1(Ki)=t(Ki)+1 fori=1,2.

Then Morimoto introduced theoriginal Morimoto conjecture:t(K1#K2)=t(K1)+t(K2)+1 if and only if neither of them is meridionally primitive.Later,Kobayashi-Rieck [35]gave a counterexample to the original Morimoto conjecture.In this counterexample,neither of these two knots is prime.Thus the modified Morimoto conjecture,also proposed by Moriah [55],is as follows:

Conjecture 7.4LetK1andK2betwo prime knots.Thent(K1#K2)=t(K1)+t(K2)+1 if and only if neither of them is meridionally primitive.

Li-Qiu [46]showed that conjecture 7.4 is false in general.More precisely,they proved that

Theorem 7.5For any integersn≥3,there is a prime but not meridionally primitive knotKso that for anym≤nand anym-bridge knotK′,t(K#K′)≤t(K).

Remark 7.6Schirmer [77]proved thatt(K1#K2)≥max {t(K1),t(K2)}.This means that the counterexample in Theorem 7.5 is optimal.

Moreover,the tunnel number of a knot is linked to a long unsolved conjecture in the Dehn surgery-the Berge conjecture.For any knotK?S3,letE(K)be the exterior spaceofKinS3.Then?E(K)is a torus.We choose a sloper??E(K),attach a 2-handle alongrtoE(K),and then attach a 3-ball to the resulted 2-sphere.ThenS3is turned into a new 3-manifoldEr(K).This process is called a Dehn surgery onK.Lickorish-Wallace [48,91]proved

Theorem 7.7Every closed orientable 3-manifold is a Dehn surgery of a link inS3.

A knotK?S3is called a Berge knot if it is doubly primitive.Here,being doubly primitive means thatKlies on a genus two Heegaard surfaceSofS3and intersects a meridian disk in one point from either side ofS.

Conjecture 7.8(Berge conjecture)If a Dehn surgery on a nontrivial knotK?S3is a Lens space,then it is a Berge knot.

A result on this conjecture is as follows:by the cyclic surgery theorem in [12],for a hyperbolic knot,only an integer Dehn surgery can yield a Lens space.Ni [61]then proved

Theorem 7.9If a knot admits a Lens space surgery,then it is a fibered knot.

Greene [18]proved

Theorem 7.10All Lens space surgeries can be obtained from doing Dehn surgeries on Berge knots.

If a knotKis doubly primitive,thent(K)=1.Therefore,the Berge conjecture can be divided into the following two parts:

Conjecture 7.2.AIf a tunnel number one knot admits a Lens space Dehn surgery,then it is doubly primitive.

Conjecture 7.2.BIf a nontrivial knotK?S3admits a Lens space surgery,then it is a tunnel number one knot.

Using combinatorial methods,Li-Moriah-Pinsky [47]announced a proof of Conjecture 7.2.A.