ON ACTION-MINIMIZING SOLUTIONS OF THE TWO-CENTER PROBLEM?
Kuo-Chang CHEN
Department of Mathematics,National Tsing Hua University,Hsinchu,Taiwan,China
E-mail:kchen@math.nthu.edu.tw
Abstract The two-center problem,also known as Euler’s three-body problem,is a classic example of integrable systems.Among its periodic solutions,planetary type solutions are periodic solutions which enclose both centers.Inspired by advances on n-body and n-center problems via variational techniques developed during the past two decades,a recent paper(Arch.Rat.Mech.Ana.2022)shows the minimizing property of planetary type solutions for any given masses of centers at fixed positions,as long as the period is above a mass-dependent threshold value.In this paper,we provide further discussions regarding this minimizing approach.In particular,we improve the above-mentioned mass-dependent threshold value by refi ning estimates for action values.
Key words two-center problem;n-body problem;variational method;collision singularity
Dedicated to Professor Banghe LI on the occasion of his 80th birthday
1 Introduction
The two-center problem concerns the motion of a free particle moving in an inverse-square central force field generated by two stationary particles.Stationary point masses are called centers.Standard examples include the gravitational force field generated by two stationary point masses,and the electrostatic force field generated by two stationary point charges.The problem has been used as an approximation for the full two-body problem where one of the bodies is an oblate or prolate ellipsoid.
In this paper,we consider the planar two-center problem where a free particle with unit mass moves on the complex plane.Its motion is governed by gravitational attraction that is due to two fixed centers with massesμ1andμ2>0.There is no loss of generality by assuming their positions to bec1=?1 andc2=1,respectively.Letz(t)∈C be the position of the free particle at timet.The equation of motion for the free particle is

The kinetic,potential,and total energies are,respectively,

The first thorough investigation of this two-center problem appeared in a memoir by Euler [6]published in 1760;for this reason the problem is also known as Euler’s three-body problem.The problem later attracted the attention of many outstanding mathematicians and physicists,including Lagrange,Legendre,Jacobi,Liouville,Darboux,Whittaker,and Pauli,among many others.It is considered one of the most classic example of integrable systems,a problem that is solvable by quadratures in terms of elliptic coordinates.Interested readers are referred to the classic treatise by Whittaker [10]and a recent book by Math′una [7]for comprehensive introductions and bibliographies.
While the problem is commonly considered well-understood,the minimizing nature of its orbits is a relatively unexplored area.Inspired by advances onn-body andn-center problems via variational techniques developed during the past two decades,a recent paper by the author [2]shows the minimizing property of planetary type periodic solutions for any given masses of centers at fixed positions,as long as the period is above a mass-dependent threshold value.This work was mainly motivated by some technical difficulties in applying local deformation arguments for action-minimizing solutions near collision singularities forn-center problems.In sharp contrast with cases of at least three centers,as noted in [2],the local deformation method alone is insufficient to exclude collision singularities from action-minimizers for the two-center problem.It is there foreessential to understand the variational nature of the two-center problem in order for further advancements in this research direction to take place.We refer readers to [1,3,4,9,11]for applications and discussions of local deformation arguments ton-center problems,and to [2]for further bibliographies.
Some improvements of the main theorem in [2]were briefly outlined in the paper,but without details;see Section 2.As an addendum to [2],in this paper we provide further discussions and details.In particular,in Section 4 we show detailed proofs for some refinements of the estimates in [2].Section 3 summarizes some observations in [2]that are essential to our proofs.
2 Variational Settings and Main Theorems
Here we briefly review the variational settings and the main theorem in [2].Then we state two refinements of the main theorem in [2].Throughout this paper we follow the notations and terminologies in [2].
Thetwo centers {c1,c2}partition the real line R into threeintervals;wecall them windows.They are

where ? and ? denote the real and imaginary parts,respectively.
A collinear configuration is called a syzygy,and the moment at which a syzygy occurs is called a syzygy moment.A classical solution of(1.1)that is transversal to the real line can be associated to a symbolic sequence consisting of 0’s,1’s,and 2’s,called syzygy sequence.The syzygy sequence records the order of the solution’s visits to windowsw0,w1,andw2.One may pick an arbitrary syzygy momentt0,let
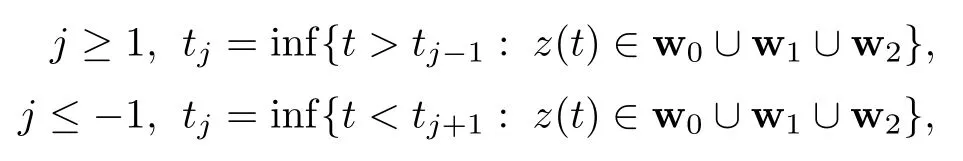
and then define the syzygy sequences=(si)by
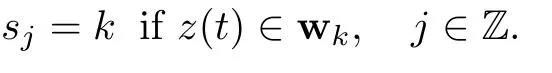
The sequence(tj)of syzygy moments can be finite or infinite.It is possible that the solution has no syzygy moment,in which case the associated syzygy sequence is empty.
We say that a pathzin C{c1,c2}realizes the syzygy sequences=(si)on the time intervalI?R if there is a strictly increasing sequence {ti}?Iof syzygy moments such that

Determining the realizability of syzygy sequences for then-center problem is a nontrivial task,and it is largely open forn≥3.See [5]for all realizable syzygy sequences in the casen=2,and their connections with symbolic dynamics associated to geodesics on flat tori.
It is natural to tackle the two-center problem by variational methods,since(1.1)is the Euler-Lagrange equation of the action functionaldefined by
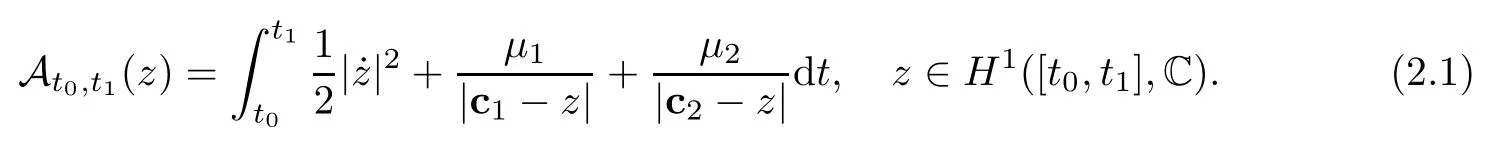
We shall fix the time interval [t0,t1]=[0,T]and denote A0,Tby AT,for simplicity.FixingT>0,critical points of ATin the Sobolev spaceH1([0,T],C)are weak solutions of(1.1)which may experience collisions.
We say a pathz∈C0([0,T],C{c1,c2})is(-shaped(pronounced“frown”-shaped)if it satisfies:
?z(0)∈w0,z(T)∈w2,
??z(t)>0 fort∈(0,T).
Defi ne

We say a classical periodic solution of(1.1)is of planetary type if it realizes the periodic syzygy sequence(···020202···).If we are able to find a classical solution in ?(02)that is perpendicular to the real line at syzygy moments,then we may periodically extend the solution to a planetary type periodic solution of(1.1).We call such an extension of the solution a canonical periodic extension.
Consider the minimization problem

The main theorem of [2]concerns the existence and minimizing property of planetary type solutions.
Theorem 2.1([2])Suppose thatT>0 satisfies

Then the minimization problem(2.2)is attained at a(-shaped solution of(1.1).The canonical periodic extension of an action minimizer is a classical solution of planetary type with a minimum period 2T.
Two refinements of Theorem 2.1 were briefly mentioned in [2]without proof.One of them is
Theorem 2.2Suppose thatT>0 satisfies

Then the conclusions of Theorem 2.1 hold.
The other refinement is confined to cases with certain mass ratios.The following special case was considered:

In this case,we have
Theorem 2.3Assume(2.5).Suppose thatT>0 satisfies
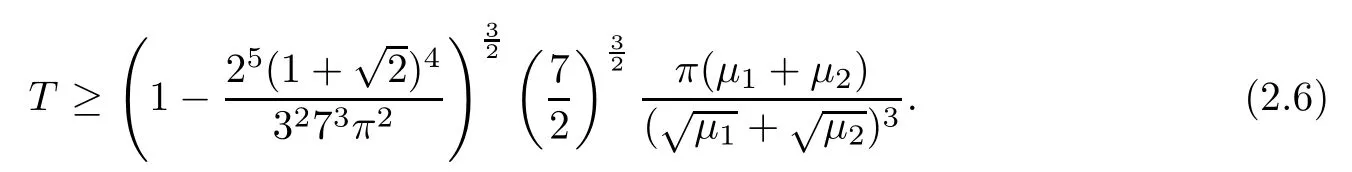
Then the conclusions of Theorem 2.1 hold.
The next two sections are devoted to proving Theorems 2.2 and 2.3.
3 Some Observations
In this section we summarize some observations in [2]that are necessary for our proofs.We present seven lemmas,one of which is a detailed version of a proposition in [2]in which the proof was omitted for brevity;see [2]for proof and further discussion of other lemmas.
A fundamental observation is the solvability of the minimization problem(2.2).
Lemma 3.1([2,Lemma 1])The action functional ATattains its infi mum on
Next,we consider the the rectilinear two-center problem;namely,(1.1)withz(t)∈R for allt.The initial value problem can be expressed

wherex?is the unique equilibrium position

The next three lemmas concern the heteroclinic ejection-collision solution of the boundary value problem(3.5).The first one provides some details for [2,Proposition 1].

Clearly,Lemma 3.2 can be extended tov0<0;the only difference is that the solutionx(t)of(3.1)becomes a decreasing diffeomorphism moving fromc2toc1.Because of time-reversal symmetry,we only need to consider the case wherev0>0.
Lemma 3.2 provides a one-to-one correspondence between the positive velocityv0at the equilibrium positionx?and the total traveling timeTfromc1toc2,whereTas a function ofv0is given by the integral in(3.4).GivenT>0,letv0>0 be the corresponding initial velocity.Consider thisv0and the unique solutionx(t)of(3.1).By translating the time variable,
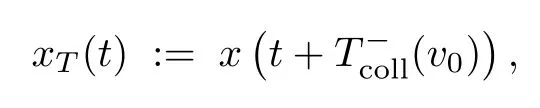
we obtain the unique solutionxT(t)to this rectilinear two-center problem that is an increasing diffeomorphism from(0,T)to(?1,1).Continuously extending this to the boundary,the procedure turns the initial value problem(3.1)withv0>0 into the boundary value problem
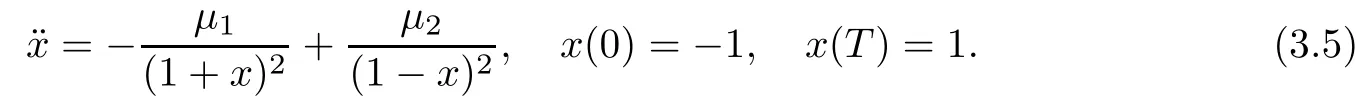
Lemma 3.3([2,Proposition 2])GivenT∈(0,∞).Letx(t)be the unique heteroclinic ejection-collision solution of the boundary value problem(3.5).Then

Lemma 3.4([2,Lemma 5])For anyT>0,the action minimizers for(2.2)have no collision on(0,T).Moreover,if an action minimizerzsatisfiesz(0)=c1orz(T)=c2,thenzis the unique heteroclinic ejection-collision solution for(3.5).
Heteroclinic ejection-collision solutions along the real line do not have well-defined syzygy sequences since they are not transversal to R.We do not confi ne the concept of“realizing syzygy sequence”to paths that are transversal to R,but the next lemma tells us that if a classical solution realizes a syzygy sequence,then it must be transversal to R.
Lemma 3.5([2,§2.2])If a classical solution of(1.1)realizes a syzygy sequence on [0,T],then it must betransversal to R,and it alternatesbetween upper and lower half planes whenever syzygies occur.
Finally,we introduce two lemmas that are useful in estimations of the action integral.
Lemma 3.6([2,Lemma 6])For anyr≥9/7,we have that
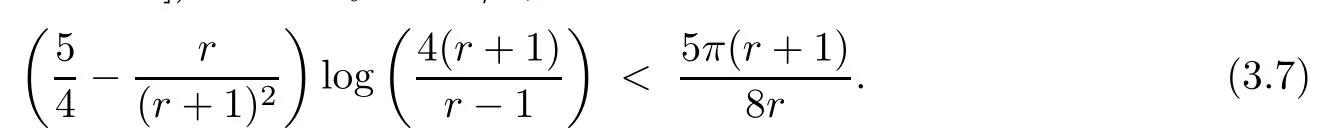
Consider the complete elliptic integral K of the first kind defined by
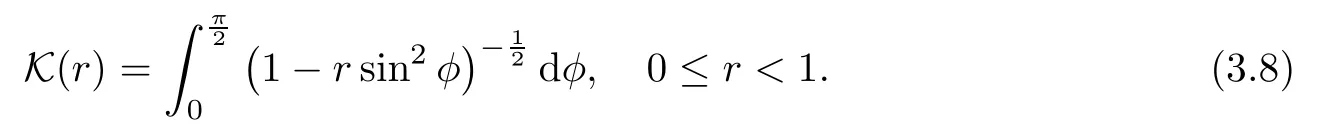
Lemma 3.7([8])The complete elliptic integral of the first kind(3.8)satisfies that
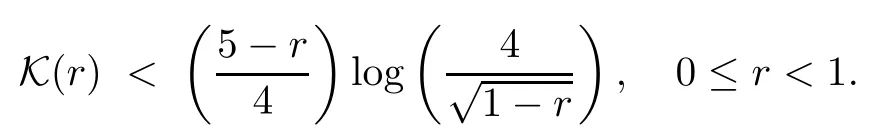
4 Proofs of Main Theorems
The main idea of the proofs is the same as that of [2,Theorem 1].We repeat the details presented in [2]for completeness.The improvement is based on finer estimates for action values.
We begin with a simple but useful upper bound estimate for real roots of some cubic polynomials.
Lemma 4.1Suppose thatα,β,γ,δ>0 satisfyδβ3≤α2.Then

ProofThere are two cases.The first case,X≥β/α,is obvious:
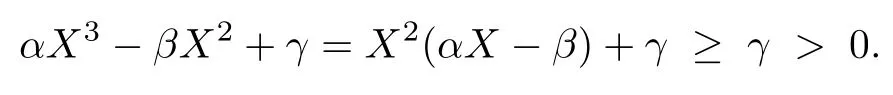
The other case,(1?γ δ)β/α≤X<β/α,follows by observing that

Consider the following auxiliary Kepler problem on the complex plane C:

This is equivalent to moving both centers of the two-center problem(1.1)to the origin.The following simple inequalities will be used multiple times:

Let
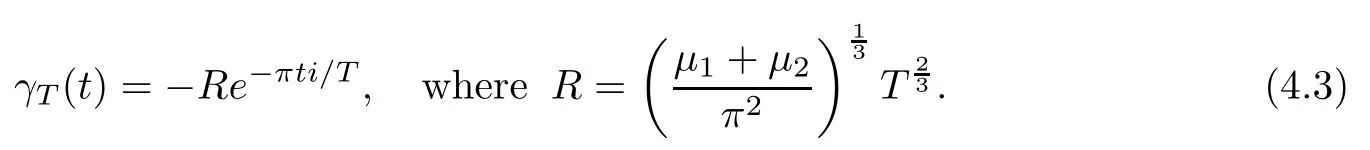
ThenγTis the 2T-periodic circular solution of(4.1)which moves clockwise from the negative real axis att=0 to the positive real axis att=T.
From(2.4)and(4.2)we have that

The integration of the kinetic energy is easy:

Combining(4.4)and(4.5),we find that
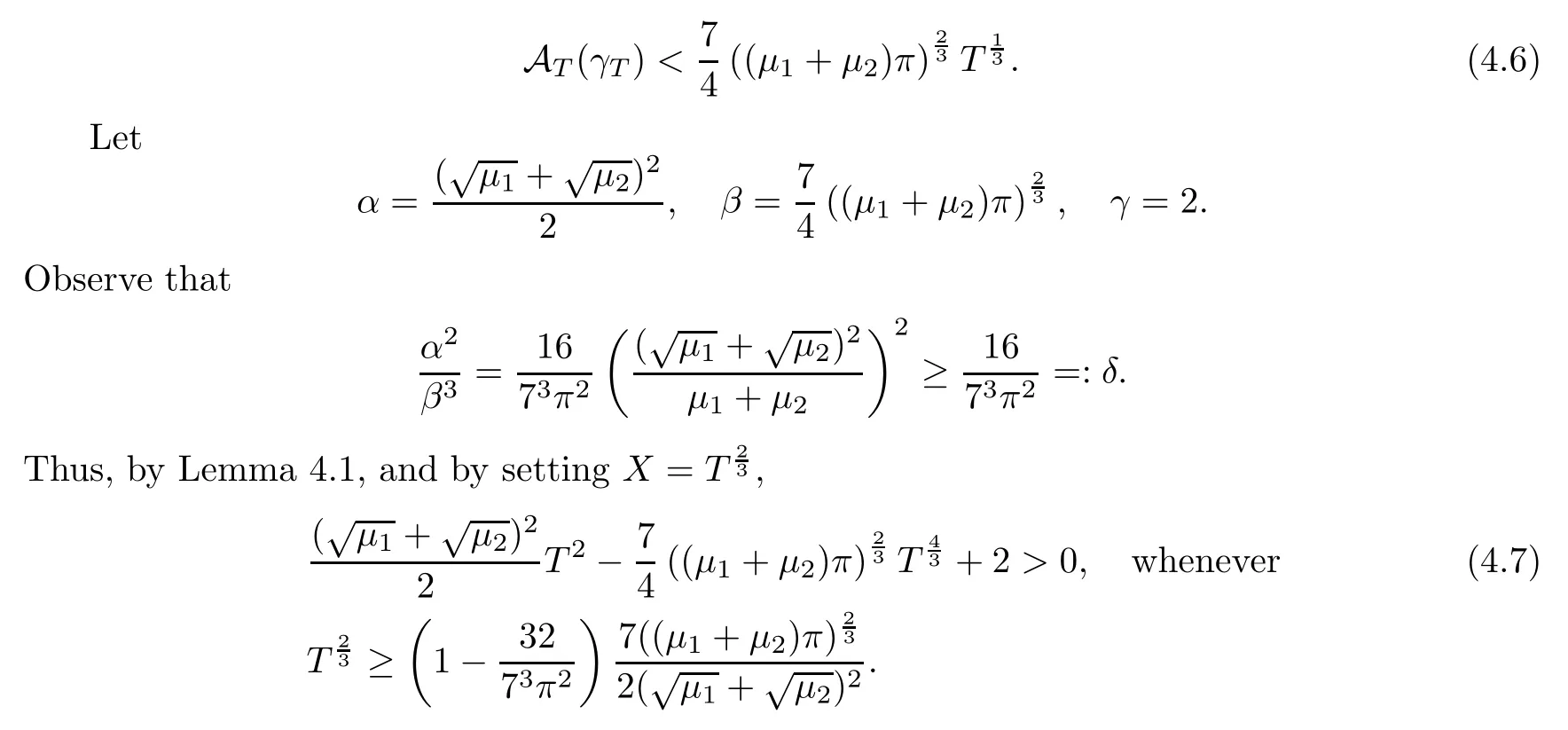
This condition onT2/3is exactly the same as the assumption(2.4).
By Lemma 3.1,there exists a minimizerzfor the minimization problem(2.2)onAssume thatzhas a collision.By Lemma 3.4,it must be the unique heteroclinic ejectioncollision solution for(3.5)fromc1toc2.Then
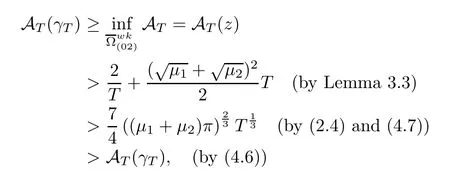
which is clearly a contradiction.Therefore,the action minimizerzmust be collision-free,so it must be a classical solution of(1.1).
The collision-free action minimizerzis homotopic to a(-shaped path relative to {0,T}within the path spaceH1([0,T],C{c1,c2}).We claim thatzis(-shaped.If we suppose otherwise,then there are consecutive syzygy momentst? The natural boundary condition obtained from the first variation of ATimplies thatzis perpendicular to R att=0 andt=T.Its canonical periodic extension is therefore a classical solution of(1.1)with a minimum period 2T,and the solution is clearly of planetary type.This finishes our proof for Theorem 2.2. Remark 4.2In our discussions for allowableT,the contribution of the term 2/Tin(3.6)was taken into consideration through an upper bound estimate for some special cubic polynomials in Lemma 4.1.One may further improve Theorem 2.2 by using Cardano’s formula to express the largest real root of cubic polynomials in more complicated closed forms. Now we prove Theorem 2.3.The proof resembles the proof of Theorem 2.2,so we skip details and only point out the main difference. Assumption(2.5)improves(4.2)to It can be easily checked that the new condition(2.6)with the same test pathγTin(4.3)also satisfies thatR>9/7,soγTis still(-shaped,and the estimate for the integration ofU(γT)in(4.4)is still valid.Following the proof of Theorem 2.2,we only need to verify that inequality(4.7)holds under the weaker assumption(2.6)onT. Following the proof of Theorem 2.2,with the sameα,β,γ,by(4.8),we have a refi nedδ: By Lemma 4.1,the condition onT2/3in(4.7)can be refi ned to This is exactly the same as(2.6).This finishes the proof for Theorem 2.3. Remark 4.3The lower bound in(2.4)improves(2.3)by about 1.41%,while with the additional mass constraint(2.5),the bound in(2.6)improves(2.3)by about 5.30%.
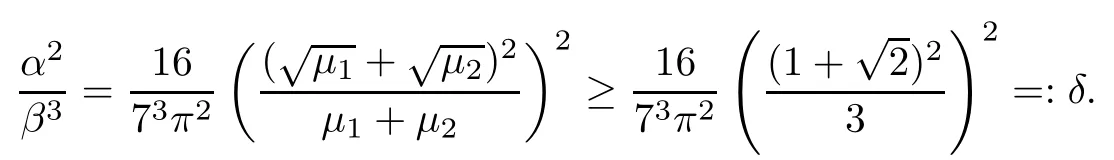

 Acta Mathematica Scientia(English Series)2022年6期
Acta Mathematica Scientia(English Series)2022年6期
- Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL WELL-POSEDNESS OF A PRANDTL MODEL FROMMHD IN GEVREY FUNCTION SPACES?
- L 2-CONVERGENCE TO NONLINEAR DIFFUSION WAVES FOR EULER EQUATIONS WITH TIME-DEPENDENT DAMPING?
- SYMBOLIC COMPUTATION FOR THE QUALITATIVE THEORY OF DIFFERENTIAL EQUATIONS?
- OPINION DYNAMICS ON SOCIAL NETWORKS?
- SOME RESULTS ON HEEGAARD SPLITTING?
- GENERIC NEWTON POLYGON OF THE L-FUNCTION OF n VARIABLES OF THE LAURENT POLYNOMIAL I?
