蔣 杰,王立春

(北京交通大學(xué) 理學(xué)院,北京 100044)

§1 引言

考慮如下的正態(tài)線性模型

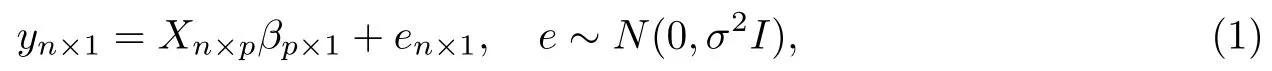
這里y=(y1,y2,...,yn)′表示響應(yīng)變量,X是秩為p的設(shè)計(jì)矩陣,β=(β1,β2,...,βp)′為未知參數(shù)向量,e是隨機(jī)誤差向量,σ2是未知的誤差方差.

在模型(1)中,眾所周知β和σ2的最小二乘估計(jì)分別為

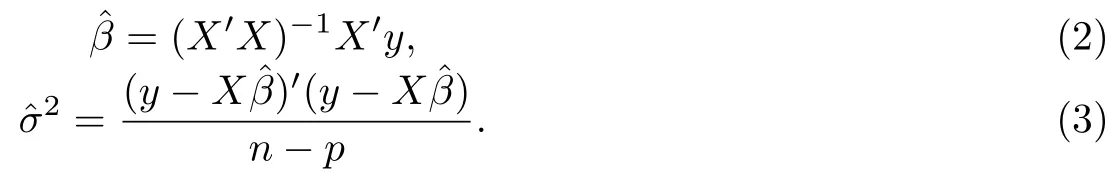
假設(shè)π(β,σ2)為β和σ2的聯(lián)合先驗(yàn)分布,結(jié)合似然函數(shù)f(y|β,σ2)可得后驗(yàn)分布密度函數(shù)h(β,σ2|y).為了獲得β和σ2的貝葉斯估計(jì),不妨記作引入如下?lián)p失函數(shù)

然而,對于這樣的多重積分的計(jì)算一般無法得到顯式解.這促使統(tǒng)計(jì)學(xué)者們在貝葉斯估計(jì)的基礎(chǔ)上做了一些研究,來解決多重積分求解困難的問題.比如,文獻(xiàn)[1]提出一種近似貝葉斯估計(jì)的方法,但是當(dāng)參數(shù)維數(shù)超過三時(shí),將涉及高階導(dǎo)數(shù),這導(dǎo)致計(jì)算過程是十分復(fù)雜冗長的.另外,MCMC算法也經(jīng)常是被用來模擬貝葉斯估計(jì)的數(shù)值解,比如Metropolis-Hastings算法,Gibbs 抽樣法等.但通過模擬得到的貝葉斯估計(jì)往往只是一個(gè)數(shù)值解,沒有顯式表達(dá)式,以至于不便從理論上討論它的統(tǒng)計(jì)性質(zhì).

近年來利用貝葉斯方法研究線性模型中參數(shù)的估計(jì)問題,在許多文獻(xiàn)[2-4]中多次被提到.對于正態(tài)線性模型中參數(shù)的貝葉斯估計(jì)目前常用的有兩種方法,其一,當(dāng)先驗(yàn)是含有未知超參數(shù)的正態(tài)分布時(shí),容易知道正態(tài)線性模型參數(shù)的后驗(yàn)分布依然是正態(tài)分布,在平方損失函數(shù)下,貝葉斯估計(jì)為后驗(yàn)期望,然后利用歷史樣本估計(jì)超參數(shù),得到經(jīng)驗(yàn)貝葉斯估計(jì)的表達(dá)式.比如,文獻(xiàn)[5]推導(dǎo)了正態(tài)線性模型中回歸系數(shù)的經(jīng)驗(yàn)貝葉斯估計(jì).文獻(xiàn)[6]研究了正態(tài)線性回歸模型中誤差方差的經(jīng)驗(yàn)貝葉斯估計(jì),并在均方誤差(MSE)準(zhǔn)則下證明了該估計(jì)優(yōu)于最小二乘估計(jì).第二種為線性貝葉斯方法,其主要思想是通過樣本統(tǒng)計(jì)量構(gòu)造待估參數(shù)的線性估計(jì),然后再通過最小化貝葉斯風(fēng)險(xiǎn)函數(shù),得到最佳的線性估計(jì)即為線性貝葉斯估計(jì),這一方法的優(yōu)點(diǎn)是不需要知道先驗(yàn)分布具體形式,只需假設(shè)先驗(yàn)分布的一些矩是存在的,就能算出線性貝葉斯估計(jì)的顯式解.在線性模型中線性貝葉斯方法最早由Rao[7]提出,在隨后的幾十年中受到了很多學(xué)者的關(guān)注和研究,參見文獻(xiàn)[8-11].尤其對于線性模型中參數(shù)的估計(jì),文獻(xiàn)[12]在假設(shè)了先驗(yàn)信息后得到了回歸系數(shù)的線性貝葉斯估計(jì),并證明了其風(fēng)險(xiǎn)函數(shù)以速率O(n?1)在減小.文獻(xiàn)[13]在一般的線性模型中推導(dǎo)了回歸系數(shù)的線性貝葉斯估計(jì),并在均方誤差矩陣(MSEM)和Pitman closeness(PC)準(zhǔn)則下證明了該估計(jì)的優(yōu)越性.隨后,文獻(xiàn)[14]研究了分塊線性模型中回歸系數(shù)的可估函數(shù)的線性貝葉斯估計(jì).特別地,文獻(xiàn)[15]在平衡損失函數(shù)下構(gòu)造了回歸系數(shù)的線性貝葉斯估計(jì),在MSEM和MSE準(zhǔn)則下證明了其優(yōu)越性,并給出了在PC準(zhǔn)則下線性貝葉斯估計(jì)優(yōu)于普通最小二乘估計(jì)的充分條件.

通過對這些文獻(xiàn)研究內(nèi)容的分析,鑒于線性貝葉斯估計(jì)具有方便使用,并且計(jì)算簡單等優(yōu)點(diǎn).文中試圖利用線性貝葉斯方法去近似貝葉斯估計(jì),并得到β和σ2組成的參數(shù)向量的線性貝葉斯估計(jì)的表達(dá)式.本文的主要研究內(nèi)容是選擇合適的統(tǒng)計(jì)量去同時(shí)構(gòu)造模型(1)中的回歸系數(shù)β和誤差方差σ2的線性估計(jì).

假設(shè)σ2的先驗(yàn)為IG(α,γ),且σ2給定下β的先驗(yàn)分布為N(μ,σ2Σ),于是σ2和β的聯(lián)合先驗(yàn)密度為

結(jié)合似然函數(shù)

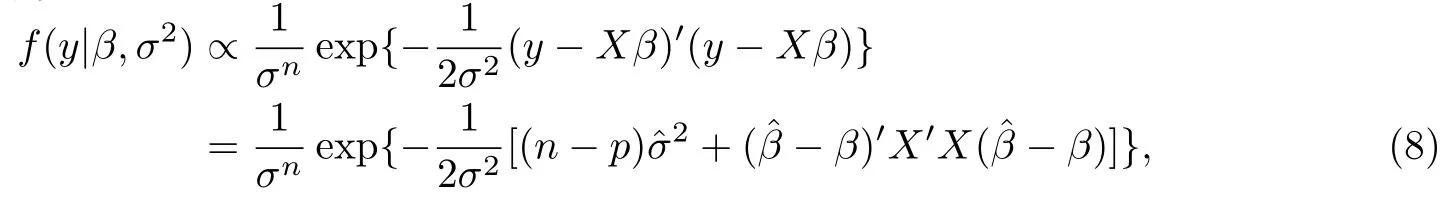
得到聯(lián)合后驗(yàn)

容易發(fā)現(xiàn)聯(lián)合后驗(yàn)和聯(lián)合先驗(yàn)有相同的分布形式,于是可以知道

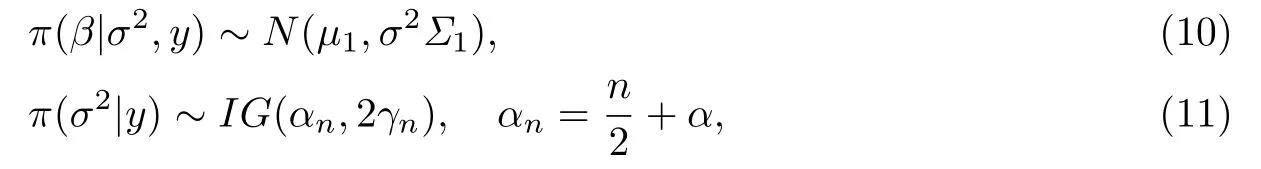
所以σ2的后驗(yàn)期望為

注意到β的邊際后驗(yàn)分布為

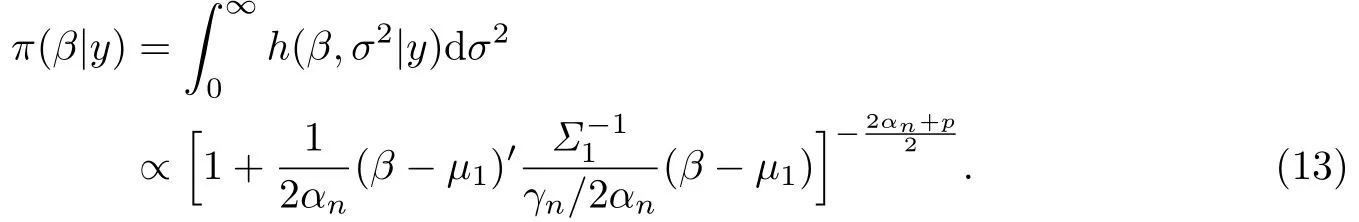
又因?yàn)樯鲜綖槎嘣猼分布密度函數(shù)的核,所以有

§2 構(gòu)造線性貝葉斯估計(jì)

假設(shè)參數(shù)向量θ=(β′,σ2)′的先驗(yàn)π(θ)屬于分布族

這里的E(y,θ)表示y和θ的聯(lián)合分布期望.

然后利用二次型期望的結(jié)果有

證首先計(jì)算貝葉斯風(fēng)險(xiǎn)函數(shù)

這里利用了如下的事實(shí)

和

和

于是有

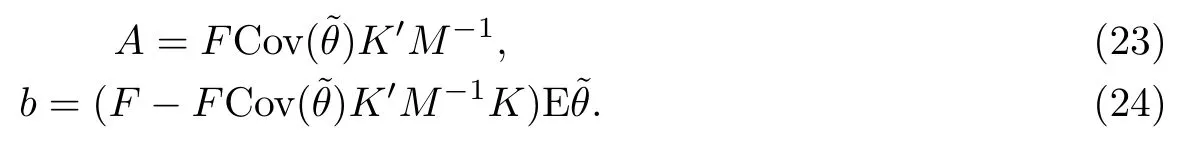
顯然地,從得到的線性貝葉斯估計(jì)的表達(dá)式以及計(jì)算過程可以知道,線性貝葉斯估計(jì)不但包含了先驗(yàn)信息,而且避免了求解貝葉斯估計(jì)時(shí)遇到的多重積分計(jì)算較困難的問題.

§3 線性貝葉斯估計(jì)的優(yōu)越性

本節(jié)在均方誤差陣準(zhǔn)則下,證明了線性貝葉斯估計(jì)相對于最小二乘估計(jì),其它結(jié)構(gòu)的線性貝葉斯估計(jì)以及極大似然估計(jì)的優(yōu)良性.首先計(jì)算的均方誤差矩陣

這里利用了這樣的事實(shí),即FK=F和W=M ?

3.1 與最小二乘估計(jì)的比較

3.2 與其它結(jié)構(gòu)的線性貝葉斯估計(jì)的比較

將W1=FWF′帶入(29) 可得

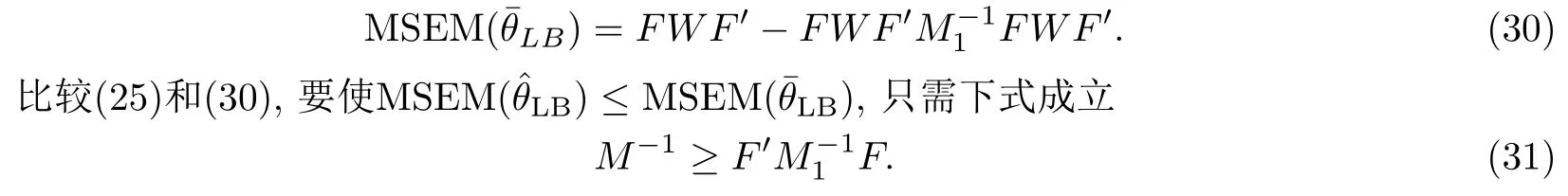
為了證明(31)成立,對矩陣F和M進(jìn)行分塊.令

和

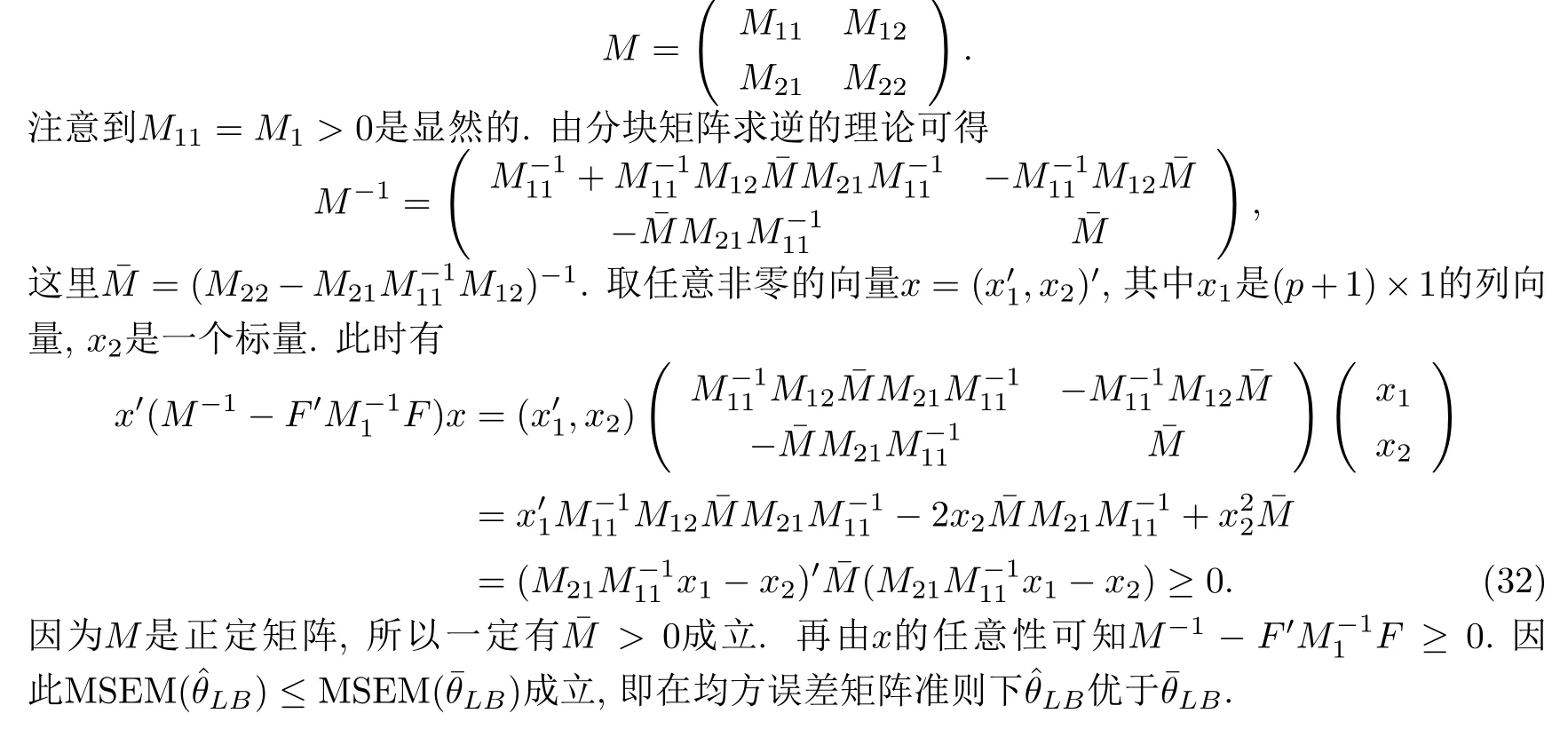
3.3 與極大似然估計(jì)的比較

首先計(jì)算如下的協(xié)方差矩陣以及方差.由二次型期望和方差的相關(guān)結(jié)論[16],容易知道

所以有

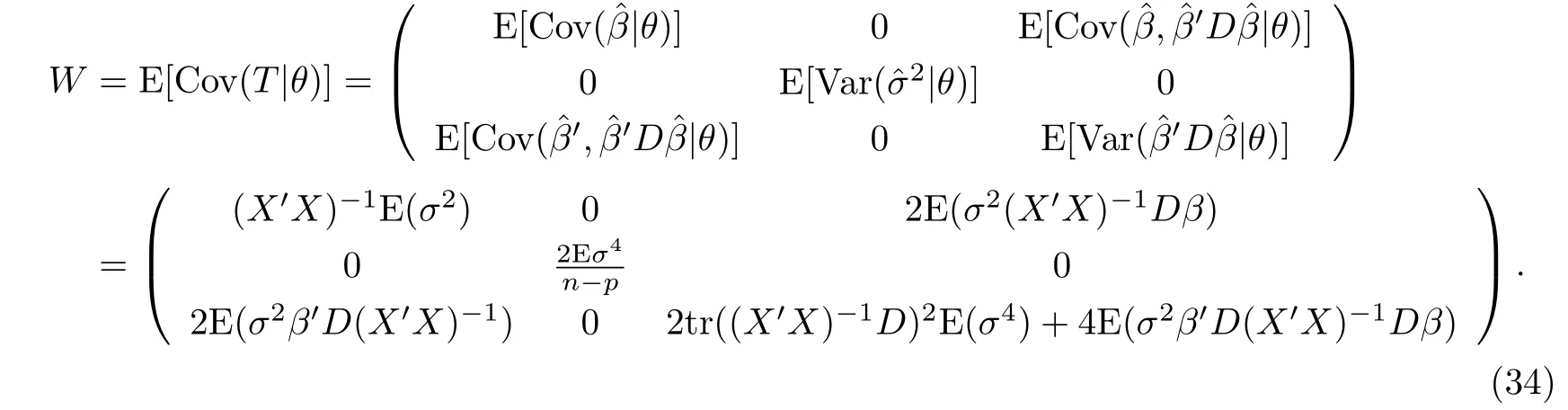
于是可得極大似然估計(jì)的均方誤差矩陣為

將(36) 和(37) 帶入(29),進(jìn)一步計(jì)算得

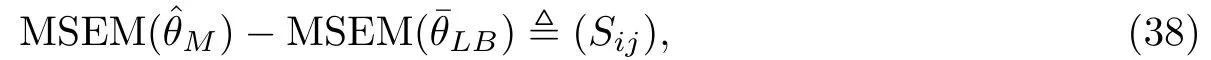
這是一個(gè)2×2的分塊矩陣,并且有

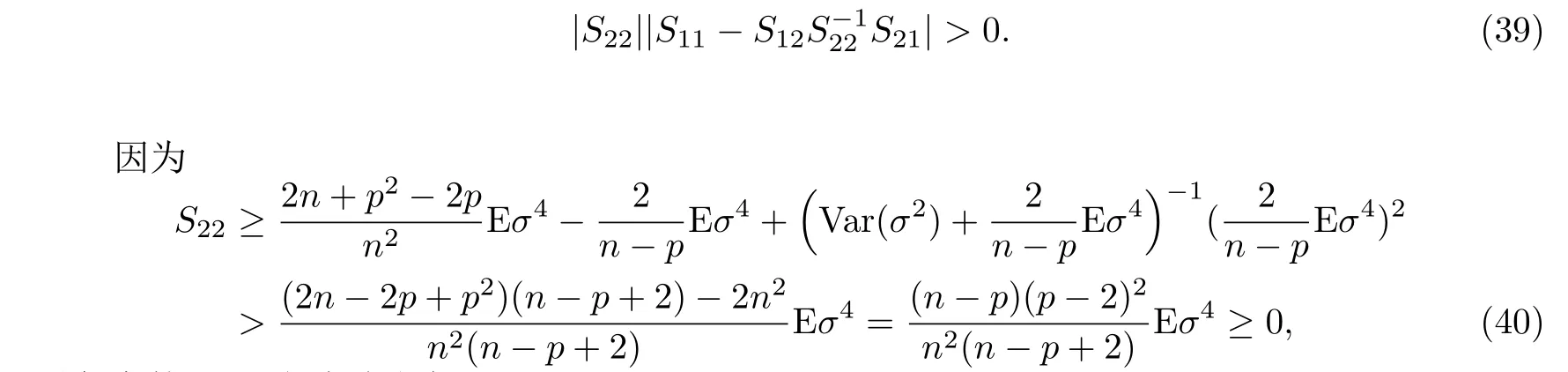
對任意的n>p上式總成立,即S22>0.

§4 數(shù)值模擬

在這一節(jié)對于幾種不同的先驗(yàn)分布,利用MCMC 算法考察了線性貝葉斯估計(jì)的數(shù)值性質(zhì).為了觀察對不同的樣本大小n的實(shí)驗(yàn)效果,取n=20,40,60,80,100,并令p=2,即β=(β1,β2)′.解釋變量X中的元素xij,i=1,2,...,n,j=1,2從標(biāo)準(zhǔn)正態(tài)分布中采樣.系數(shù)向量β以及方差σ2的值從先驗(yàn)中取得.y從正態(tài)分布N(Xβ,σ2I)中模擬得到.為了獲得θ的貝葉斯估計(jì)需要假設(shè)β和σ2的先驗(yàn)分布.對于先驗(yàn)分布的選擇,選取了如下兩種不同的先驗(yàn)形式.

情形一假設(shè)在σ2給定下β服從正態(tài)分布N(μ,σ2Σ),σ2服從均勻分布U(a,b).因此聯(lián)合后驗(yàn)密度函數(shù)為

這里I(a,b)(σ2)表示示性函數(shù).在式子(4) 給出的損失函數(shù)下,為y給定下的θ的后驗(yàn)期望的值,此時(shí)可以知道通過對式子(5)和(6) 積分求后驗(yàn)期望是無法實(shí)現(xiàn)的,所以選擇利用Metroplis with Gibbs[17]算法模擬的數(shù)值解.首先根據(jù)(43) 計(jì)算β和σ2的滿條件后驗(yàn)分布分別為

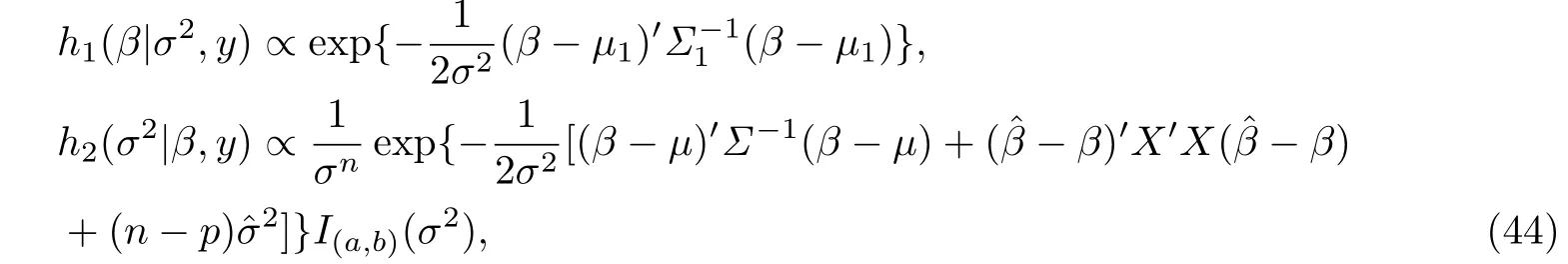
這里Σ1=注意,從上式可以知道β的滿條件后驗(yàn)分布是均值為μ1,協(xié)方差陣為σ2Σ1的多元正態(tài)分布,所以可以直接從N(μ1,σ2Σ1)中采樣,而σ2的滿條件分布不是常見的分布形式,因此,利用Metroplis方法采樣,并選取均勻分布作為其建議分布.然后利用Metroplis with Gibbs算法對β和σ2進(jìn)行采樣.具體步驟如下

(1) 給定β和σ2的初始值β(0),σ2(0);用β(j),σ2(j)表示β,σ2在第j步的值,j=0,1,2,···,N;

(2)從N(μ1,σ2(j)Σ1)中產(chǎn)生β(j+1);

(3)用Metroplis方法對σ2進(jìn)行采樣;

(a) 從建議分布中產(chǎn)生候選點(diǎn)σ2?;

(b) 從均勻分布U(0,1)中產(chǎn)生U;

(c) 判斷：若U則接受σ2?,并令σ2(j+1)=σ2?,否則令σ2(j+1)=σ2(j).

(4) 重復(fù)步驟(2)-(3);

(5) 計(jì)算后面N ?N0次實(shí)驗(yàn)的平均值得到貝葉斯估計(jì).

情形二假設(shè)在σ2給定下β服從自由度為v的多元t分布tp(μ,σ2Σ,v),σ2服從卡方分布χ2(t).此時(shí)聯(lián)合后驗(yàn)密度函數(shù)為

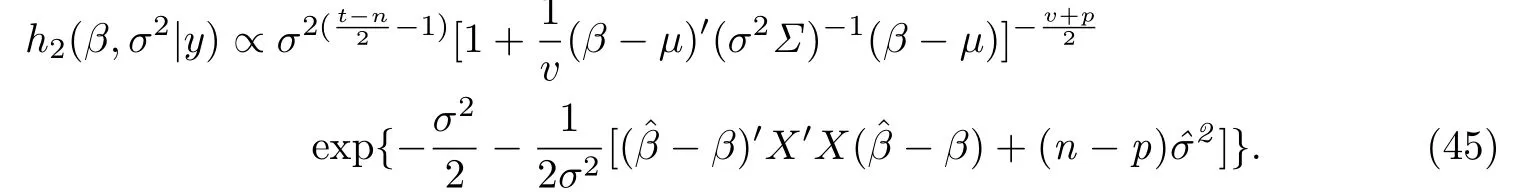
為了考察θ的線性貝葉斯估計(jì)和貝葉斯估計(jì)分別與θ的真實(shí)值的差異程度,利用了如下歐氏距離公式

在表1給出的四種非共軛先驗(yàn)的情況下,從表2和表3中可以看出,文中選擇的統(tǒng)計(jì)量T所構(gòu)造的到真實(shí)值的距離,小于由統(tǒng)計(jì)量T1所構(gòu)造的到真實(shí)值的距離.這說明更接近θ.這一結(jié)論與理論結(jié)果也是相一致的.

表1 先驗(yàn)分布的參數(shù)取值

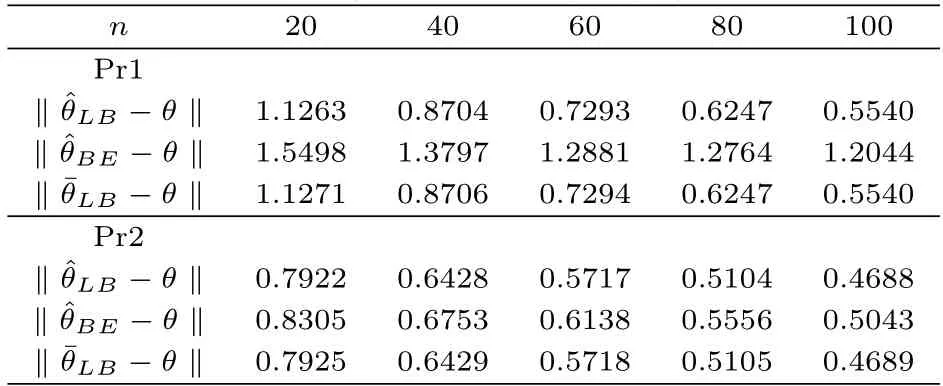
表2 在先驗(yàn)Pr1 和Pr2下距離的值

表3 在先驗(yàn)Pr3 和Pr4 下距離的值

并且可以發(fā)現(xiàn)對于不同的先驗(yàn)分布,都小于說明當(dāng)貝葉斯估計(jì)無法得到顯示解時(shí),利用線性貝葉斯估計(jì)去估計(jì)真實(shí)值,并不遜色于利用Metroplis with Gibbs算法得到的貝葉斯估計(jì).所以從貝葉斯統(tǒng)計(jì)角度,除了經(jīng)典的貝葉斯估計(jì),線性貝葉斯估計(jì)同樣有不錯(cuò)的性質(zhì).另外,還可以發(fā)現(xiàn),當(dāng)n越大,這些距離都呈現(xiàn)減小的趨勢,這表明樣本越多獲取的信息越多,此時(shí)的估計(jì)量對待估參數(shù)的近似效果越好.

事實(shí)上,通過對數(shù)似然函數(shù)

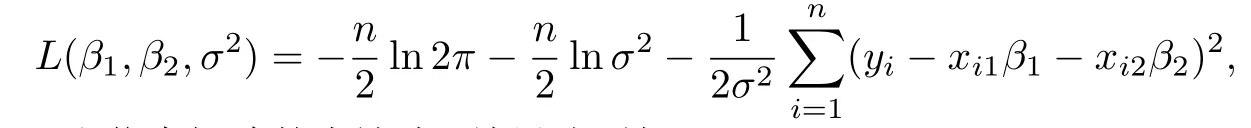
可以計(jì)算出Lijk和信息矩陣的表達(dá)式.結(jié)果分別如下

表4 先驗(yàn)分布的參數(shù)取值

從表5的數(shù)值結(jié)果以及曲線圖1都可以看出,說明更接近于真實(shí)值.且隨著樣本n的增大,兩條曲線的差異越來越小.另一方面從的表達(dá)式可以知道,當(dāng)θ的維數(shù)增加時(shí),高階微分的計(jì)算復(fù)雜度也隨之增加,相比之下,線性貝葉斯估計(jì)的表達(dá)式的獲得過程更簡單直接.所以由模擬結(jié)果和理論研究分析可知線性貝葉斯估計(jì)是一種有效的估計(jì).

表5 在先驗(yàn)Pr5和Pr6下,距離‖?θ ‖和‖?θ ‖的值

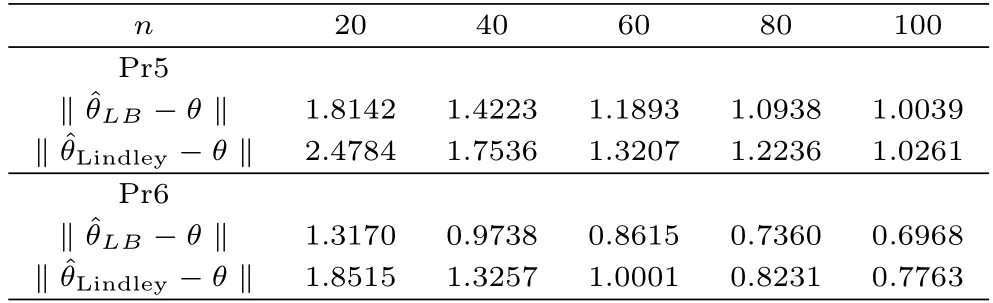
表5 在先驗(yàn)Pr5和Pr6下,距離‖?θ ‖和‖?θ ‖的值

圖1 在Pr5和Pr6 下,距離‖ ?θ ‖和‖ ?θ ‖隨樣本的變化情況

另外,為了從數(shù)值模擬方面再一次驗(yàn)證用文中提到的統(tǒng)計(jì)量T構(gòu)造線性貝葉斯估計(jì)的合理性.在引言中給出的正態(tài)逆伽馬分布下,對的接近程度進(jìn)行討論.表6 給出了先驗(yàn)分布的參數(shù)取值.表7 展示了估計(jì)量以及距離的值.

表6 先驗(yàn)分布的參數(shù)取值

表7 在Pr7下參數(shù)估計(jì)和距離的值

§5 數(shù)值實(shí)例

在這一部分利用教育學(xué)家測試的21個(gè)兒童的智力測試數(shù)據(jù)[16]，來驗(yàn)證線性貝葉斯估計(jì)的有效性.變量y表示某種智力指標(biāo),X1為兒童的年齡(以月為單位),數(shù)據(jù)為y=((95,71,83,91,102,87,93,100,104,94,113,96,83,84,102,100,105,57,121,86,100)′,X1=(15,26,10,9,15,20,18,11,8,20,7,9,10,11,11,10,12,42,17,11,10)′.記X=(1,X1)以及β=(β0,β1)′,這里1是元素全為1的列向量.通過這些數(shù)據(jù),建立智力隨年齡變化的關(guān)系.考慮如下線性回歸模型

這里β和σ2是未知參數(shù).對這個(gè)模型,主要目的是利用文中提到的線性貝葉斯方法去估計(jì)未知參數(shù)β和σ2.在表8給出的兩種先驗(yàn)下,分別計(jì)算了的距離.

表8 β和σ2的先驗(yàn)分布

從表9可以看出,與其它幾種估計(jì)相比,線性貝葉斯估計(jì)與貝葉斯估計(jì)非常接近,而Lindley近似作為貝葉斯估計(jì)的另一種近似估計(jì),在這里表現(xiàn)得相對比較糟糕,并且表達(dá)式也很繁瑣復(fù)雜.因此,可以說線性貝葉斯估計(jì)是一種合理可行的估計(jì).

表9 不同先驗(yàn)分布下的距離

§6 結(jié)論

本文在正態(tài)線性模型中,利用線性貝葉斯方法同時(shí)估計(jì)了其回歸系數(shù)β和誤差方差σ2,并在只假設(shè)先驗(yàn)的某些矩存在而不知道先驗(yàn)的具體形式的情況下,得到了參數(shù)向量θ=(β′,σ2)′的線性貝葉斯估計(jì)的表達(dá)式.然后在均方誤差矩陣準(zhǔn)則下,證明了線性貝葉斯估計(jì)優(yōu)于經(jīng)典的最小二乘估計(jì)和極大似然估計(jì).從數(shù)值模擬方面,選取了四種不同的先驗(yàn)分布,利用Metroplis with Gibbs 算法模擬得到θ的貝葉斯估計(jì)并且從數(shù)值模擬的結(jié)果中可以看出更接近參數(shù)真值.作為對比,引入Lindley 近似通過分析發(fā)現(xiàn)有一個(gè)更好的近似表現(xiàn).因此,從模擬的角度再次驗(yàn)證了線性貝葉斯估計(jì)的優(yōu)越性.更重要的是,在參數(shù)向量高維情況下,Lindley 近似的表達(dá)式涉及高階微分的計(jì)算,且計(jì)算過程隨著待估參數(shù)維數(shù)的增大也越來越復(fù)雜,此時(shí)想要獲得Lindley 近似的表達(dá)式是非常困難的,然而,維數(shù)的增大對于線性貝葉斯估計(jì)的表達(dá)式的獲得并沒有影響.所以待估參數(shù)維度增大時(shí),相對而言,線性貝葉斯估計(jì)計(jì)算更容易,表達(dá)式也更簡潔.最后,用一個(gè)數(shù)值實(shí)例驗(yàn)證了線性