凌 羚,李光輝,張崇岐

(1.廣州大學(xué) 經(jīng)濟(jì)與統(tǒng)計學(xué)院,廣東廣州 510006;2.凱里學(xué)院 理學(xué)院,貴州凱里 556011)

§1 引言

混料試驗在眾多領(lǐng)域都有著廣泛的應(yīng)用.2011年Cornell[1]將混料模型應(yīng)用于雛雞飼養(yǎng)及水果飲料配方研發(fā).2019年,Goos和Hamidouche[2]將混料應(yīng)用于雞尾酒實驗,Zijlstra等[3]通過混料模型來描述流動性預(yù)算的偏好和偏好異質(zhì)性.近年來,對于混料模型的最優(yōu)設(shè)計研究,一般都集中于D-,A-,I-等單目標(biāo)最優(yōu)準(zhǔn)則.例如,李光輝等[4]研究了具有復(fù)雜約束混料試驗的漸近D-最優(yōu)設(shè)計;劉妙玲等[5]研究了一階半變系數(shù)混料模型的D-最優(yōu)設(shè)計;朱小淵等[6]研究了缺失項二階混料模型的I-最優(yōu)設(shè)計.

現(xiàn)在隨著試驗成本的不斷上升,研究人員使用傳統(tǒng)的單目標(biāo)試驗優(yōu)化方法去處理多個目標(biāo)時,不僅會額外增加試驗次數(shù),還會浪費大量的人力,物力資源和時間成本.例如,考慮某一混料模型的D-與A-最優(yōu)性.D-最優(yōu)設(shè)計在使參數(shù)向量的置信橢球體積達(dá)到最小時,往往會存在某些參數(shù)估計值的方差較大;而A-最優(yōu)設(shè)計在使得模型中未知參數(shù)最小二乘估計的方差之和達(dá)到最小時,又會令置信橢球體的體積變大.因此,本文的目標(biāo)是找到一種高效的多目標(biāo)優(yōu)化設(shè)計,既能平衡各種目標(biāo)的效率,又能為更重要的目標(biāo)提供更高的效率.

眾多學(xué)者提出了各種不同的方法研究多目標(biāo)優(yōu)化試驗問題.1971年,Stigler[7]在研究多項式回歸模型最優(yōu)試驗設(shè)計時,提出了C-約束D-最優(yōu)設(shè)計.該設(shè)計在考慮單最優(yōu)準(zhǔn)則對參數(shù)估計的約束效果同時,仍然允許對模型進(jìn)行檢驗.1983 年,Mikulecka[8]利用凸優(yōu)化技術(shù)研究了C-約束D-最優(yōu)性,基于懲罰方法導(dǎo)出了C-約束D-最優(yōu)設(shè)計的數(shù)值算法.1988年,Lee[9]基于Fréchet導(dǎo)數(shù)給出了一個約束最優(yōu)設(shè)計的充要條件.1990年,Dette[10]提出了適用于多項式回歸模型的組合優(yōu)化設(shè)計.1994年,Cook和Wong[11]證明了在一定條件下,約束最優(yōu)設(shè)計和組合最優(yōu)設(shè)計這兩種尋求多目標(biāo)優(yōu)化設(shè)計的方法是等價的.1998年,Huang和Wong[12]提出了一種基于序貫方法構(gòu)造非線性模型的多目標(biāo)局部最優(yōu)設(shè)計.2008年,Atkinson[13]給出了在模型識別和參數(shù)估計之間提供特定平衡的DT-優(yōu)化設(shè)計.這些研究大部分都是基于兩目標(biāo)組合優(yōu)化設(shè)計.2015年,Hyun和Wong[14]構(gòu)建了一種基于logistic模型的三目標(biāo)優(yōu)化設(shè)計,并對每一個目標(biāo)給定了用戶感興趣的效率.以上文獻(xiàn)幾乎都是研究的多項式回歸模型多目標(biāo)優(yōu)化設(shè)計,并不適用于混料模型.2012年,Zhang[15]等提出了混料模型的多目標(biāo)優(yōu)化設(shè)計,該文基于兩分量二階混料規(guī)范多項式模型,通過圖檢驗法,導(dǎo)出了兩目標(biāo)約束最優(yōu)設(shè)計.

本文由四個部分組成.§1為引言;§2介紹了含定性因子的混料模型和兩種常見的多目標(biāo)優(yōu)化設(shè)計方法;§3基于q分量s水平混料分類模型,通過對研究者感興趣的目標(biāo)設(shè)置相應(yīng)的權(quán)重,導(dǎo)出了模型的多目標(biāo)優(yōu)化設(shè)計,并由方差函數(shù)證明了組合設(shè)計的最優(yōu)性;§4給出結(jié)論并對多目標(biāo)優(yōu)化設(shè)計未來的研究進(jìn)行了展望.

§2 模型與最優(yōu)準(zhǔn)則

2.1 含定性因子的Scheffé模型

混料試驗設(shè)計通常假設(shè)響應(yīng)變量y僅與試驗中各分量比例x1,x2,···,xq有關(guān),而與總量無關(guān).由各分量比例所確定的q ?1維試驗域可表示為

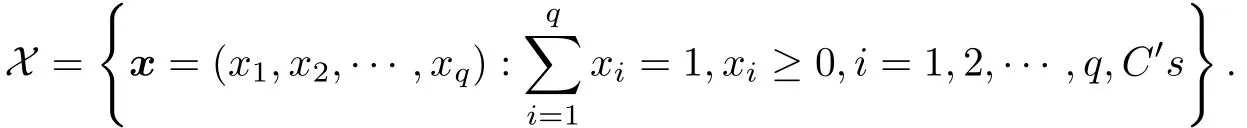
其中C′s為附加約束條件.當(dāng)模型不含附加約束時,稱之為q ?1維正規(guī)單純形,記作Sq?1.在混料設(shè)計中使用較多的是Scheffé中心多項式模型

其特點是在不降低模型階數(shù),保持預(yù)測精度的條件下減少了試驗次數(shù).

但在許多實際問題中,響應(yīng)不僅僅受到各混料分量的影響,還會受到其他變量的影響.這類模型可表示為

其中模型(2)一次項與交互項部分都受到定性因子影響;模型(3)的一次項與交互項部分分別為因子效應(yīng)及固定效應(yīng);模型(4)的一次項與交互項部分分別為固定效應(yīng)及因子效應(yīng).例如,某醫(yī)師希望對治療新冠肺炎的兩種不同的藥物-連花清瘟顆粒和清肺排毒湯的療效進(jìn)行比較,兩種藥物的藥效對患者性別之間的差異可視為模型(3),(4)中的第一部分,藥物的固定藥效可視為兩模型的第二部分.

2.2 最優(yōu)設(shè)計

一個k點設(shè)計可表示為

其中x={x1,x2,···,xk},r={r(x1),r(x2),···,r(xk)}分別表示設(shè)計ξ的試驗點集與各點對應(yīng)的測度,且=1.令所有設(shè)計的全集Ξ為一個設(shè)計空間,最優(yōu)設(shè)計就是確定一個設(shè)計ξ ∈Ξ,使得該設(shè)計信息矩陣M(ξ)在某種意義下達(dá)到最優(yōu).D-最優(yōu)與A-最優(yōu)設(shè)計在應(yīng)用領(lǐng)域非常普遍.D-最優(yōu)設(shè)計是將信息矩陣的行列式最大化,從而使得參數(shù)向量的置信橢球體積最小.即

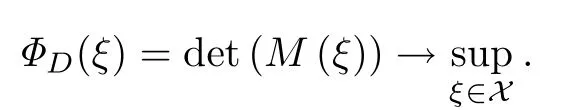
一個設(shè)計ξ是D-最優(yōu)設(shè)計的充分必要條件是

其中m是模型中未知參數(shù)向量β的維數(shù),ψD(x,ξ)是設(shè)計ξ在D-準(zhǔn)則下的方差函數(shù),當(dāng)ψD(x,ξ)在柱點處等于0時,則設(shè)計ξ是D-最優(yōu)設(shè)計.

A-最優(yōu)設(shè)計是將信息矩陣逆的跡極小化,從而使模型未知參數(shù)最小二乘估計的方差之和達(dá)到最小,即

若一個設(shè)計ξ是A-最優(yōu)的,則有

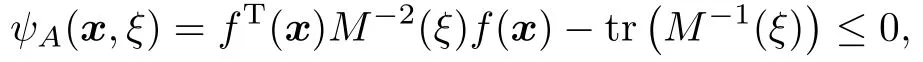
且ψA(x,ξ)在柱點處等于0.

約束最優(yōu)設(shè)計與組合最優(yōu)設(shè)計是研究者常用的兩種求解多目標(biāo)最優(yōu)設(shè)計的方法.約束最優(yōu)設(shè)計一般假設(shè)試驗必須滿足兩個截然不同的目標(biāo)φ1和φ2,它們分別表示在信息矩陣上定義的主要和次要目標(biāo).為了平衡這些相互競爭的目標(biāo),可以選擇一個主要目標(biāo)效率不低于某一常數(shù)時,次要目標(biāo)效率盡可能高的設(shè)計[7].令?c表示存在常數(shù)約束c的約束最優(yōu)設(shè)計集,當(dāng)設(shè)計ξ受限于φ1(ξ)≥c時,有

容易證明?c是一個凸集.此時最優(yōu)設(shè)計ξc應(yīng)該滿足ξc=arg max?c φ1(ξ).

組合最優(yōu)設(shè)計是基于兩目標(biāo)函數(shù)φ1和φ2的加權(quán)平均[10],可表示為

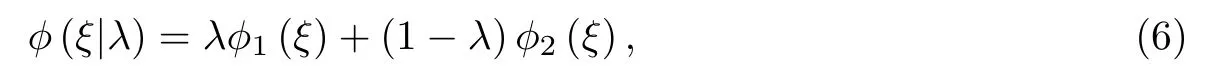
其中0≤λ ≤1.最開始研究者試圖通過選擇一個恰當(dāng)?shù)臋?quán)重λ,來反映兩個不同目標(biāo)的相對重要性,但實際表明,λ值的選取與設(shè)計的效率之間沒有明顯的聯(lián)系.例如,當(dāng)λ=0.5時,并不能表明研究者對兩目標(biāo)的興趣是一致的.

§3 主要結(jié)果

3.1 兩目標(biāo)最優(yōu)混料分類試驗設(shè)計

基于q分量s水平二階混料分類模型,研究者感興趣的目標(biāo)分別為模型的D-最優(yōu)與A-最優(yōu)性.D-最優(yōu)設(shè)計可以使信息矩陣的行列式達(dá)到最大,從而使模型中未知參數(shù)估計建立的置信橢球體體積達(dá)到最小.但在構(gòu)造模型的D-最優(yōu)設(shè)計時,會存在少數(shù)參數(shù)估計值的方差較大,因此第二個目標(biāo)考慮它的A-最優(yōu)設(shè)計,希望模型中未知參數(shù)估計的諸分量方差之和盡可能的小.

以Ds={1,2,···,s}表示定性因子的s個處理,記z=(j,x)∈?,?=Ds ×X為混料試驗域與定性因子構(gòu)成的直積試驗域.則試驗域?上的設(shè)計可以表示為兩部分設(shè)計的直積形式,即ζ(j,x)=η(j)×ξ(x),這里η是試驗域Ds上的設(shè)計,ξ(x)是試驗域X上的設(shè)計.則ζ具有如下形式

對于混料分類模型試驗域?中的任一設(shè)計ζ,用效率來衡量其優(yōu)劣情況,設(shè)計ζ在不同準(zhǔn)則下的效率分別為

其中,detM(ζD)為D-最優(yōu)設(shè)計信息矩陣的行列式,trM?1(ζA)為A-最優(yōu)設(shè)計信息矩陣逆的跡,eD(ζ)和eA(ζ)分別為某一設(shè)計ζ的D-效率和A-效率.如同2.2節(jié)敘述的約束最優(yōu)準(zhǔn)則,研究者希望當(dāng)主要目標(biāo)效率較高時,次要目標(biāo)效率盡可能的高.因此本文的主要目的是使兩目標(biāo)效率和達(dá)到最大

把模型(1)寫成矩陣乘積形式

可得出模型(11)在設(shè)計ζ下的信息矩陣為

其中D=diag{η(1),η(2),···,η(s)},η=[η(1),η(2),···,η(s)]T.信息矩陣行列式為

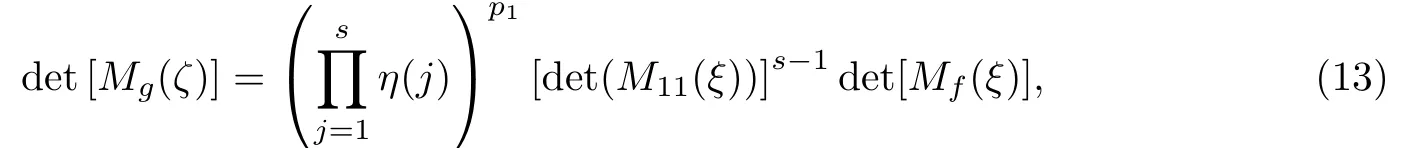
信息矩陣的逆的跡為

其中D22(ξ)=

對于模型(3),混料區(qū)域上的設(shè)計ξ使用二階廣義中心設(shè)計點集C{q,2}來安排試驗,=(x1,x2,···,xq)T與=(x1x2,x1x3,···,xq?1xq)T分別為二階中心多項式的一次項與交互項函數(shù)向量.定性因子部分取其試驗域Ds上的均勻設(shè)計,記

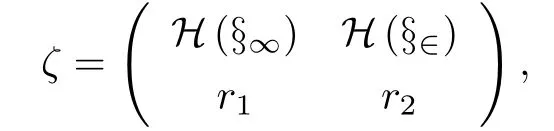
這里x1=(1,0,···,0)T,x2=(1/2,1/2,···,0)T分別是單純形上的頂點和棱中點,H(xi)={xi1,xi2,···,xini}是xi,i=1,2的置換點集,所對應(yīng)的各點測度滿足n1r1+n2r2=1.以

分別表示方差函數(shù)在兩類設(shè)計點處的值.若設(shè)計ζ是D-最優(yōu)的,一方面應(yīng)有

另一方面應(yīng)有

對于3分量4水平二階混料分類模型,可以求得

令函數(shù)

隨著r1∈(0,1/n1)的變換,m(r1)的變化過程如圖1(左)所示,可知模型的D-最優(yōu)測度為r1=0.2354,行列式值為0.042.圖1(右)顯示了h1(r1)與h2(r1)的變化過程,可見當(dāng)r1=時,h1(r1)與h2(r1)交于一點,該點坐標(biāo)為=(0.2354,15).

圖1 3分量4水平二階混料分類模型D-最優(yōu)設(shè)計結(jié)果

由(7)式可得設(shè)計ζ的D-效率為

同理模型在A-最優(yōu)準(zhǔn)則下的方差函數(shù)為

易知當(dāng)r1=0.1838時,該設(shè)計的D-,A-效率和最大,值為1.962.此時每個目標(biāo)效率如下

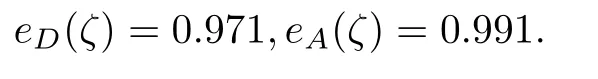
由下面不等式可確定權(quán)重α,使得該設(shè)計滿足對應(yīng)的組合最優(yōu)性條件

其中α ∈[0,1],且當(dāng)x為柱點時等號成立.表1和圖2給出了不同權(quán)重下D-,A-兩準(zhǔn)則組合最優(yōu)設(shè)計相應(yīng)效率及效率和.由圖2可以看出,隨著α值的增大,設(shè)計ζ?在D-最優(yōu)準(zhǔn)則下的效率不斷上升,在A-最優(yōu)準(zhǔn)則下的效率不斷下降.由表1可知,當(dāng)設(shè)計ζ為D-最優(yōu)或A-最優(yōu)設(shè)計時,它的效率和都無法達(dá)到最大.當(dāng)α=0.99時,效率和最大.此時每個目標(biāo)效率如下:

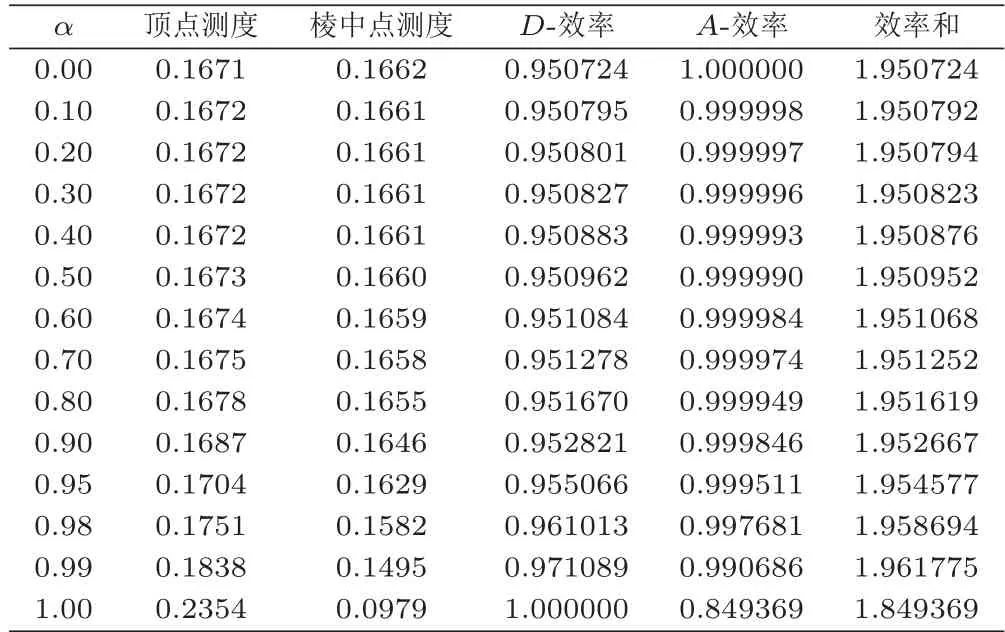
表1 D-, A-兩準(zhǔn)則組合最優(yōu)設(shè)計及其效率和

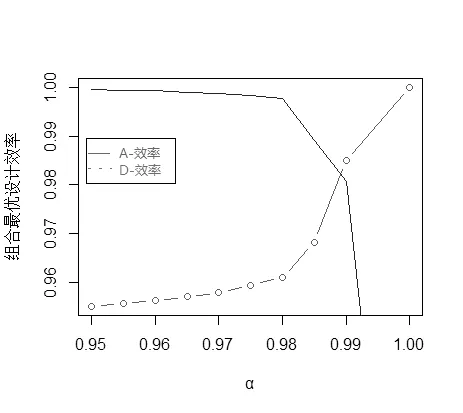
圖2 組合最優(yōu)設(shè)計效率

直接通過求解效率和達(dá)到最大時的測度,然后再解出相應(yīng)測度滿足組合最優(yōu)性時的權(quán)重值,得到新的組合最優(yōu)設(shè)計ζ?.與以往的方法相比,僅需一步求最值,少了大量迭代過程,計算更為簡便,結(jié)果更加精確.

3.2 多目標(biāo)最優(yōu)混料試驗設(shè)計

上節(jié)討論了q分量s水平混料分類模型的兩目標(biāo)最優(yōu)設(shè)計,而對于混料可加模型,Becker模型等其它混料模型的多目標(biāo)最優(yōu)設(shè)計,該方法同樣適用.眾所周知單純形-中心設(shè)計具有在不降低模型階數(shù)且保持預(yù)測精度的條件下減少了試驗次數(shù)的優(yōu)點,因此基于二分量二階混料中心多項式模型,作者感興趣的三個目標(biāo)分別為模型的R-最優(yōu),D-最優(yōu)與A-最優(yōu)性.

設(shè)計ξ是R-最優(yōu)設(shè)計[16]當(dāng)且僅當(dāng)方差函數(shù)ψR(x,ξ)滿足條件

且ψR(x,ξ)在柱點處等于0.其中R=diag{1/M11,1/M22,...,1/Mmm},Mii,i=1,2,...,m是M?1(ξ)中主對角線上的元素.

眾所周知對于二分量二階混料中心多項式模型,它的R-最優(yōu)設(shè)計的試驗點在單純形的頂點和棱中點上,且易算出測度為r1=0.375.設(shè)計ξ的信息矩陣為

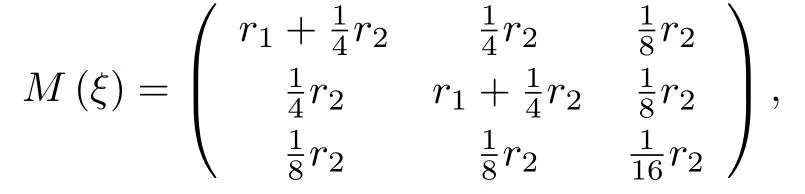
相關(guān)矩陣為

由式(7),(8)可知設(shè)計ξ的A-效率,D-效率和R-效率分別為

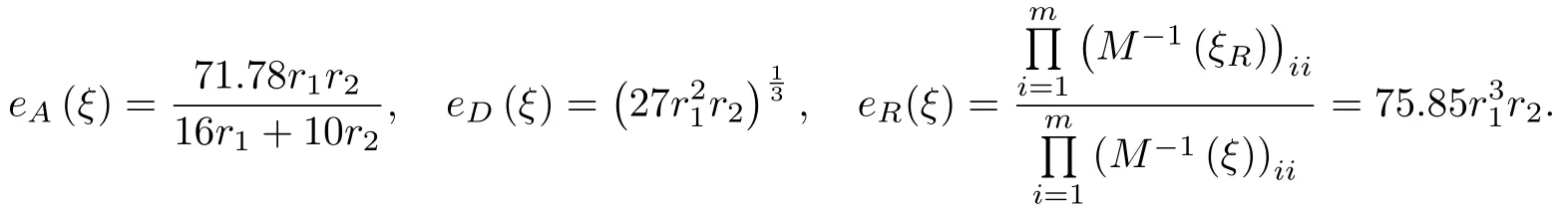
進(jìn)而最大化這三個最優(yōu)準(zhǔn)則的效率和可寫為

進(jìn)一步求得r1=0.30,r2=0.40.此時三目標(biāo)效率和達(dá)到最大,值為2.79.再通過下面不等式可確定每個感興趣目標(biāo)的相應(yīng)權(quán)重,使得設(shè)計ξ?滿足組合最優(yōu)性條件

以往求解3個或更多目標(biāo)優(yōu)化設(shè)計問題時,一般先考慮任意兩個目標(biāo)確定雙目標(biāo)優(yōu)化設(shè)計,然后依次配對其余的目標(biāo),最終確定多目標(biāo)優(yōu)化設(shè)計.然而該方法計算復(fù)雜,還會出現(xiàn)一定誤差.本文提出的方法僅需求得多個目標(biāo)效率和最大時的測度,計算簡單,且可以得到精確的結(jié)果.

§4 進(jìn)一步討論與總結(jié)

多目標(biāo)最優(yōu)設(shè)計的提出,改進(jìn)了傳統(tǒng)單目標(biāo)最優(yōu)設(shè)計在實際應(yīng)用中的不足.本文研究了q分量s水平混料分類模型的多目標(biāo)最優(yōu)設(shè)計問題,通過求解不同準(zhǔn)則下效率和取極值時的測度,得到新的多目標(biāo)最優(yōu)設(shè)計ξ?,并證明了該設(shè)計滿足相應(yīng)組合最優(yōu)性.實例證明,該方法同樣適用于求解3個或更多目標(biāo)優(yōu)化設(shè)計問題,且計算更為簡便,結(jié)果更加精確.在之后的研究中,可以考慮如何尋找不同用戶指定效率的穩(wěn)健多目標(biāo)優(yōu)化設(shè)計,并證明該設(shè)計是否滿足相應(yīng)最優(yōu)性.