譚佳玲,曾 鑫,吳劉倉

(昆明理工大學(xué)理學(xué)院,云南昆明 650504)

§1 引言

現(xiàn)實問題中,數(shù)據(jù)幾乎都具有偏斜,完全對稱情況十分罕見.若忽略偏態(tài)特征,會導(dǎo)致結(jié)論偏倚,降低效率.實際上,數(shù)據(jù)的偏斜特征能夠由偏態(tài)分布描述,過去的大量研究表明,使用偏正態(tài)分布有效解決了數(shù)據(jù)偏斜問題.另外,數(shù)據(jù)常因各種各樣的原因產(chǎn)生缺失.例如,在抽樣調(diào)查與實驗中,數(shù)據(jù)受到無回答的干擾,或由人為原因?qū)е氯笔?目前對均值建模的理論已十分成熟,在偏正態(tài)數(shù)據(jù)下,為了更好地認(rèn)識眾數(shù)的性質(zhì),對眾數(shù)建模是有意義的.

近年來,對缺失與偏態(tài)數(shù)據(jù)的研究已經(jīng)取得一定成果.在缺失數(shù)據(jù)方面,對缺失值進(jìn)行插補(bǔ)是處理缺失值的方法之一,楊曉倩[1]將缺失數(shù)據(jù)的插補(bǔ)方法進(jìn)行了分類,同時比較各種插補(bǔ)方法的插補(bǔ)效果,明確了插補(bǔ)方法的選擇需要依靠不同數(shù)據(jù)特性具體分析;廖祥超[2]討論了九種常用的插補(bǔ)方法,系統(tǒng)地介紹了插補(bǔ)方法的使用,并基于已知數(shù)據(jù)集從插補(bǔ)誤差與建模效果兩方面比較了插補(bǔ)效果;Hadeed等[3]利用短期監(jiān)測到的空氣污染數(shù)據(jù),研究數(shù)據(jù)缺失問題與缺失值的估算方法.在偏正態(tài)數(shù)據(jù)方面,Azzalini[4]首次對偏正態(tài)分布做了系統(tǒng)研究,提出了含偏度與峰度的偏正態(tài)分布.之后,Azzalini[5]簡單討論了數(shù)據(jù)服從偏正態(tài)分布時,如何進(jìn)行回歸分析.后續(xù)許多學(xué)者在偏正態(tài)數(shù)據(jù)下研究了回歸模型.例如,Ferreira等[6]研究了偏正態(tài)線性回歸模型的診斷分析,簡化了EM算法中條件期望表達(dá)式的求解.Hu等[7]基于偏正態(tài)部分函數(shù)線性模型進(jìn)行統(tǒng)計推斷,提出了基于函數(shù)主成分分析的極大似然估計方法,并檢驗了方差齊次性.

隨著缺失數(shù)據(jù)與偏態(tài)數(shù)據(jù)領(lǐng)域的研究越來越成熟,部分學(xué)者開始將二者結(jié)合起來.例如,Lin等[8]對數(shù)據(jù)不完全的多元偏正態(tài)模型進(jìn)行分析,并在隨機(jī)缺失機(jī)制下,提出了一種解析簡單的ECM算法,用于計算參數(shù)估計,同時使用單值插補(bǔ)的方法填補(bǔ)缺失值.Liu和Lin[9]研究了不完全數(shù)據(jù)下的偏正態(tài)因子分析模型,提出了一種分析可行的ECM算法,用于隨機(jī)缺失機(jī)制下的參數(shù)估計.另外,吳劉倉等[10]研究了在帶有缺失的偏正態(tài)數(shù)據(jù)下線性回歸模型的統(tǒng)計推斷,比較了幾種插補(bǔ)方法的插補(bǔ)效果.吳劉倉等[11]分別基于偏正態(tài)分布,偏t正態(tài)分布,研究了聯(lián)合均值與方差模型的插補(bǔ)方法與參數(shù)估計.

綜上所述,目前對于偏態(tài)數(shù)據(jù)有一定的研究,對缺失數(shù)據(jù)的研究較為豐富,基于缺失數(shù)據(jù)進(jìn)行統(tǒng)計推斷的理論較為成熟.雖然帶有缺失的偏正態(tài)數(shù)據(jù)的回歸模型也有一定的研究成果,但在帶有缺失的偏正態(tài)數(shù)據(jù)下眾數(shù)回歸模型的統(tǒng)計推斷問題涉及很少.原因之一在于雖然一維偏正態(tài)分布適用于研究數(shù)據(jù)呈單峰且有偏的情形,但在參數(shù)模型的框架下,對眾數(shù)建模需要知道分布的眾數(shù)的顯示表達(dá).考慮到眾數(shù)作為“最多水平”的標(biāo)志值,在偏正態(tài)數(shù)據(jù)下對眾數(shù)建模是有意義的,曹幸運(yùn)等[12]在偏正態(tài)數(shù)據(jù)下針對眾數(shù)建立了回歸模型,研究了該模型的統(tǒng)計診斷問題.此外,就插補(bǔ)方法而言,雖有學(xué)者提到了變量服從偏正態(tài)分布時可采用眾數(shù)作為插補(bǔ)值,但還沒有學(xué)者在回歸模型中進(jìn)行插補(bǔ)效果試驗.

本文的結(jié)構(gòu)安排如下:§2介紹偏正態(tài)分布的性質(zhì),提出眾數(shù)回歸模型;§3利用高斯牛頓迭代法對模型參數(shù)進(jìn)行極大似然估計;§4通過Monte Carlo 模擬證實本文所提方法的有效性;§5對實例進(jìn)行分析,論證本文所構(gòu)建的模型與使用的方法是合理可行的;§6給出本文的結(jié)論.

§2 偏正態(tài)數(shù)據(jù)下的眾數(shù)回歸模型

根據(jù)Azzalini[4]對于偏正態(tài)分布的研究,若隨機(jī)變量Y服從偏正態(tài)分布,將其記為Y ～SN(μ,σ2,λ).其中,μ為位置參數(shù),σ2為尺度參數(shù),λ為偏度參數(shù).偏正態(tài)分布的概率密度函數(shù)表示為

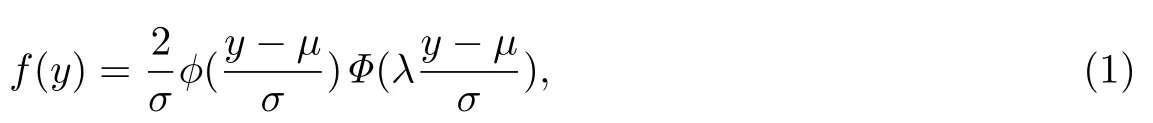
其中,φ(·) 和Φ(·)分別表示標(biāo)準(zhǔn)正態(tài)分布的概率密度函數(shù)和累積分布函數(shù).

Azzalini的研究結(jié)果[12]表明偏正態(tài)數(shù)據(jù)的眾數(shù)是唯一的,并且給出在一般情況下,眾數(shù)的計算式為Mode(Y)=μ+σM0(λ).對于一般的λ而言,很難得到M0(λ) 的顯式表達(dá)式,于是采用數(shù)值方法去近似它.Azzalini[12]提出一種簡單但實際上十分精確有效的近似

2.1 偏正態(tài)分布的隨機(jī)表示

依據(jù)Henze[14]的研究,定義隨機(jī)變量Z是具有密度函數(shù)φ(y;λ)=2φ(y)Φ(yλ) 的連續(xù)隨機(jī)變量,也就是Z ～SN(0,1,λ),可描述隨機(jī)變量Y的表達(dá)式為Y=μ+σZ.進(jìn)而可以得到隨機(jī)變量Y的隨機(jī)表示(SR)為

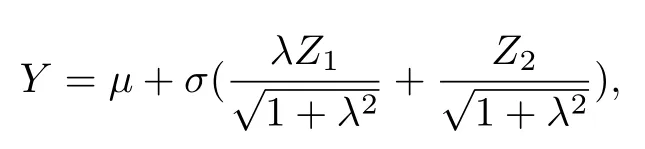
上式有Z1～TN(0,1;(0,+∞)),Z2～N(0,1),其中TN(·) 表示標(biāo)準(zhǔn)正態(tài)分布在區(qū)間(0,+∞)上的截尾,則Y服從位置參數(shù)μ,尺度參數(shù)σ2,偏度參數(shù)λ的偏正態(tài)分布.

2.2 偏正態(tài)眾數(shù)回歸模型

由眾數(shù)計算式Mode(yi)=μi+σM0(λ)與回歸模型(2),可知位置參數(shù)的表達(dá)式為

其次,根據(jù)式(1)和式(3),可得yi的概率密度為

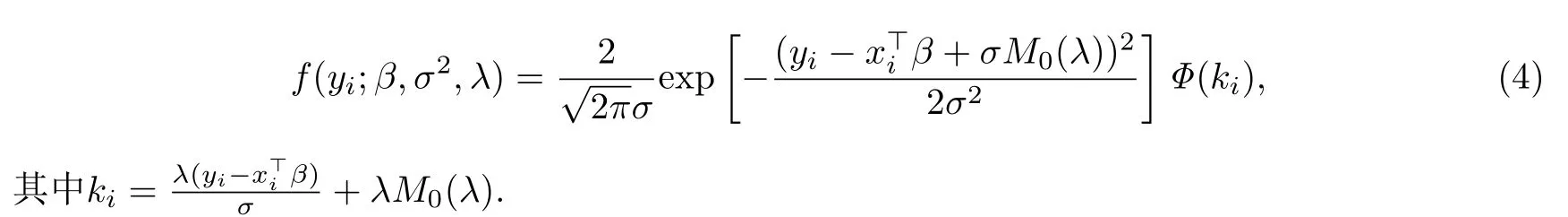
在以上模型中,yi為第i個響應(yīng)變量,服從位置參數(shù)為μi,尺度參數(shù)為σ2,偏度參數(shù)為λ的偏正態(tài)分布.xi=(xi1,···,xip)是可以觀測的協(xié)變量,β=(β1,···,βp)是維數(shù)為p×1維的未知眾數(shù)回歸系數(shù).

§3 偏正態(tài)數(shù)據(jù)下眾數(shù)回歸模型的參數(shù)估計

3.1 完全偏正態(tài)數(shù)據(jù)下的極大似然估計

對于眾數(shù)回歸模型,由式(3)與(4)可得似然函數(shù)為

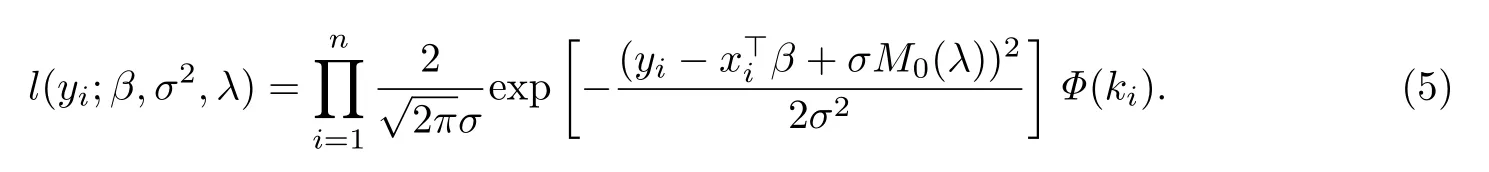
并令θ=(β,σ2,λ),則對數(shù)似然函數(shù)L(β,σ2,λ)為

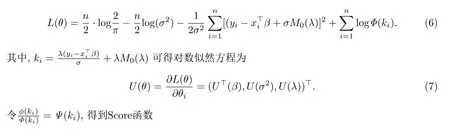
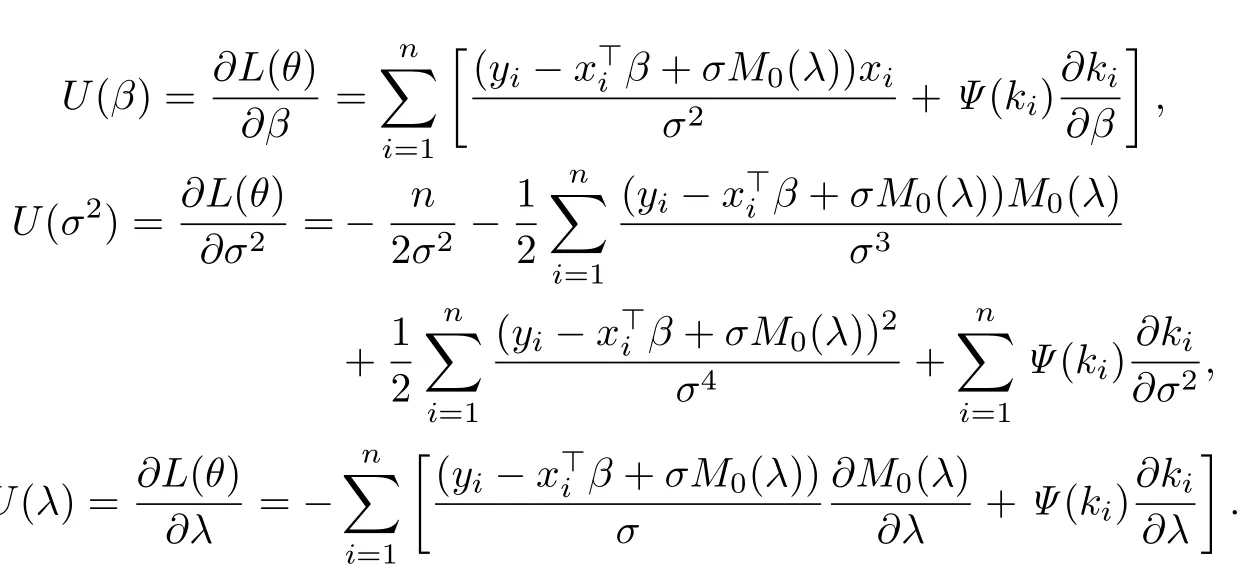
對數(shù)似然函數(shù)L(θ)關(guān)于參數(shù)θ=(β,σ2,λ)的Hessian矩陣為

步驟1更新θ(1)=θ(0)+D(θ(0));

步驟2將θ(1)記為當(dāng)前迭代,更新θ(2)=θ(1)+D(θ(1));

···

步驟3重復(fù)迭代至第t次,將θ(t)作為當(dāng)前參數(shù)再迭代,得到θ(t+1)=θ(t)+D(θ(t));

步驟4直到||θ(t+1)?θ(t)||2≤η,η為預(yù)定的充分小的正數(shù),如η=10?6,則認(rèn)為迭代收斂,取θ(t+1)作為極大似然估計的近似值.

3.2 帶有缺失的偏正態(tài)數(shù)據(jù)下的極大似然估計

缺失機(jī)制一般分為三類,分別是完全隨機(jī)缺失,隨機(jī)缺失與非隨機(jī)缺失.在對含有缺失數(shù)據(jù)的數(shù)據(jù)集進(jìn)行處理之前,明確數(shù)據(jù)的缺失機(jī)制是必要的.本文為了比較插補(bǔ)方法,選取隨機(jī)缺失作為缺失機(jī)制.缺失數(shù)據(jù)下的參數(shù)估計方法之一是將缺失數(shù)據(jù)集通過選用的插補(bǔ)方法補(bǔ)全后,應(yīng)用高斯牛頓迭代法進(jìn)行極大似然估計.

接下來介紹采用的幾種插補(bǔ)方法,首先約定無缺失數(shù)據(jù)的樣本點(diǎn)為有應(yīng)答項,則有缺失數(shù)據(jù)的樣本點(diǎn)為無應(yīng)答項.定義f為應(yīng)答變量,表示目標(biāo)樣本中是否存在缺失項.fi=1為第i個單元有應(yīng)答,不存在缺失項.fi=0為第i個單元無應(yīng)答,存在缺失項.y為目標(biāo)變量,稱為插補(bǔ)值,則插補(bǔ)后的完全數(shù)據(jù)為

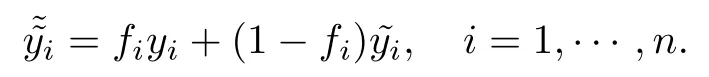
(1)均值插補(bǔ)(EI)

均值插補(bǔ)[1]指在缺失數(shù)據(jù)集中,計算目標(biāo)缺失變量中有應(yīng)答項的均值,后用該均值替代缺失數(shù)據(jù)真值.主要分為以下兩種.

單一均值插補(bǔ)指分別計算各目標(biāo)變量中有應(yīng)答項的均值,然后插補(bǔ)到相應(yīng)的缺失項中.每一目標(biāo)變量只能有一個均值,用這個均值插補(bǔ)到對應(yīng)的所有缺失項中.單一均值插補(bǔ)簡單地利用一個均值代替缺失值,嚴(yán)重扭曲樣本分布,總體方差與協(xié)方差被低估,不適合偏態(tài)數(shù)據(jù)下的參數(shù)估計,一般更適合變量服從或近似服從正態(tài)分布的情況.插補(bǔ)值理論式為

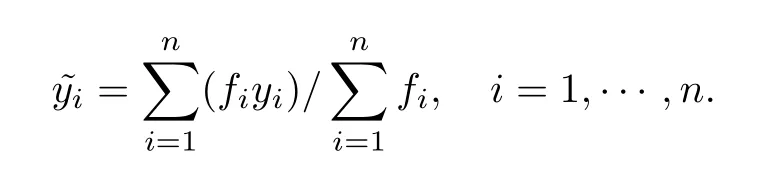
分層均值插補(bǔ)指在利用均值這個簡單變量進(jìn)行插補(bǔ)之前,根據(jù)變量的屬性,對總體進(jìn)行分層,使各層中的各項數(shù)值盡可能相近,每一層中求解單一均值,各層的單一均值分別代替各層的缺失值,得到分層均值插補(bǔ)數(shù)據(jù)集

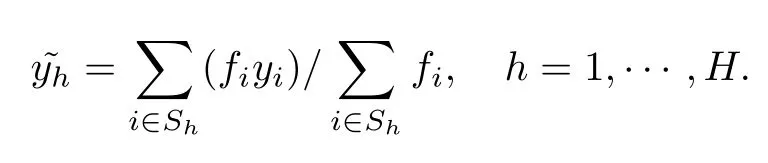
其中H表示分層總數(shù),Sh表示第h層所在的數(shù)據(jù)集,為該層的插補(bǔ)值.分層的層數(shù)H需考慮缺失項多少,然后由總體樣本劃分適合的層距,每層之間各項數(shù)值盡可能相近.每一層對應(yīng)一個單一均值,顯然提高了均值插補(bǔ)的效果,因此在大樣本的條件下,可使用分層均值插補(bǔ).插補(bǔ)值理論式為

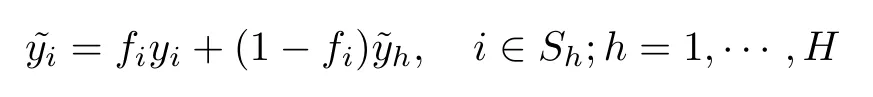
(2)眾數(shù)插補(bǔ)(MI)

眾數(shù)插補(bǔ)指分別計算各目標(biāo)變量中的眾數(shù),用眾數(shù)替代缺失數(shù)據(jù)真值.變量服從或近似服從偏正態(tài)分布,考慮眾數(shù)作為插補(bǔ)值[2].插補(bǔ)值理論式為

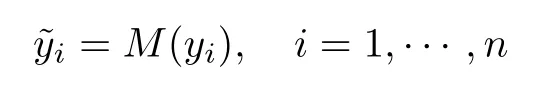
眾數(shù)代表了數(shù)據(jù)的大多數(shù)水平,在缺失偏正態(tài)分布數(shù)據(jù)下,根據(jù)偏正態(tài)分布的特性,數(shù)據(jù)主要集中在偏斜方向,導(dǎo)致均值,中位數(shù),眾數(shù)是不等的,從數(shù)據(jù)集的角度出發(fā),采取眾數(shù)作為缺失項的插補(bǔ)值,更適合偏正態(tài)數(shù)據(jù)下的參數(shù)估計.

(3)回歸插補(bǔ)(RI)

回歸插補(bǔ)[2]指先根據(jù)數(shù)據(jù)集是否含有缺失項,將其劃分為兩類.一是含有缺失項的缺失數(shù)據(jù)集Dmis,二是不含缺失項的完全數(shù)據(jù)集Dcom.其次,在完全數(shù)據(jù)集Dcom中,建立缺失變量Y關(guān)于輔助變量X的回歸模型,最后預(yù)測缺失數(shù)據(jù).

對于缺失變量yi ～SN(μi,σ2,λ),給定x條件下y的密度函數(shù)為fθ(y|x),其中θ=(β,σ2,λ).將數(shù)據(jù)集按是否缺失的標(biāo)準(zhǔn)進(jìn)行劃分,得到完全數(shù)據(jù)集Dcom包含y1,···,yk,缺失數(shù)據(jù)集Dmis包含yk+1,···,yn.利用觀測值(x1,y1),···,(xk,yk)并采用完全數(shù)據(jù)下參數(shù)的極大似然估計方法對參數(shù)θ進(jìn)行估計,從而得到這樣就可以對缺失值yj(j=k+1,···,n)進(jìn)行獨(dú)立的參數(shù)隨機(jī)插補(bǔ).插補(bǔ)值理論式為

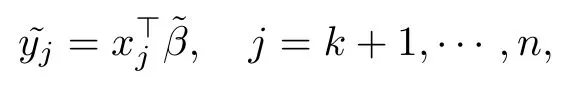
§4 Monte Carlo模擬

本節(jié)對§3提出的完全數(shù)據(jù)下模型參數(shù)的極大似然估計與利用三種插補(bǔ)方法插補(bǔ)后的缺失數(shù)據(jù)下模型參數(shù)的極大似然估計進(jìn)行模擬研究.此外,模擬傳統(tǒng)均值回歸模型的參數(shù)估計,與本文提出的方法進(jìn)行比較.均值回歸模型下的回歸系數(shù)用α表示.用均方誤差(MSE)來評價估計效果,等同于權(quán)衡參數(shù)的精度,假設(shè)α0,β0,,λ0是參數(shù)α,β,σ2,λ的真值,定義均方誤差(MSE)如下.

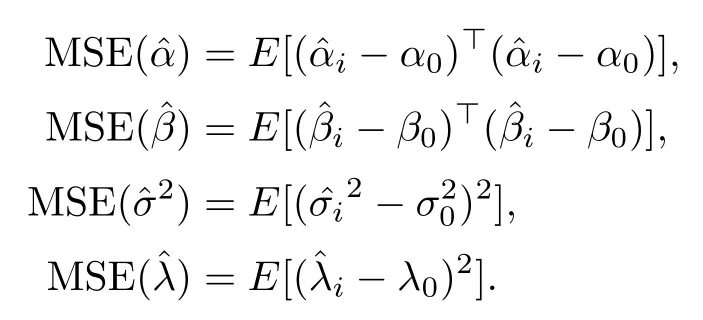
4.1 完全數(shù)據(jù)下的Monte Carlo模擬

模擬數(shù)據(jù)基于模型(2)與§2偏正態(tài)分布的隨機(jī)表示得出.取參數(shù)的真值為α0=(5,?6,7),β0=(5,?6,7),=4,分別取λ0=?5,λ0=5.在完全樣本量n分別為100,200,300的條件下,重復(fù)模擬1000次.模擬結(jié)果見表4.1.

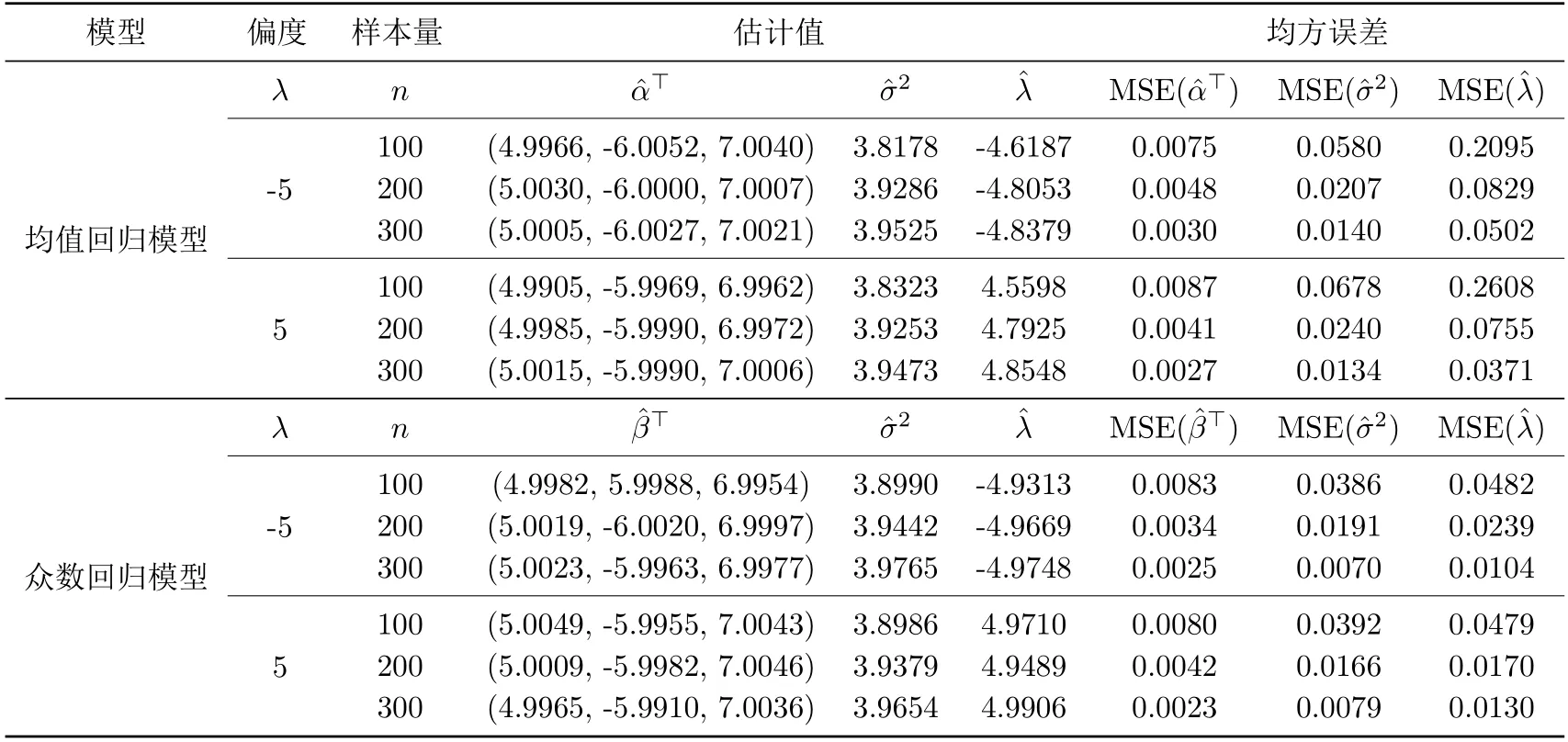
表4.1 完全數(shù)據(jù)下均值和眾數(shù)回歸模型的參數(shù)估計結(jié)果比較

從表4.1可知,無論偏度的取值是正還是負(fù),隨著樣本量n的增大,所有參數(shù)的估計值都越來越接近真值,均方誤差越來越小.特別地,樣本量n相同時,眾數(shù)回歸模型所得估計結(jié)果對應(yīng)的均方誤差(MSE)小于均值回歸模型所得估計結(jié)果對應(yīng)的均方誤差(MSE),說明本文提出的眾數(shù)回歸模型比傳統(tǒng)均值回歸模型更優(yōu),且取得比較理想的效果.

4.2 缺失數(shù)據(jù)下的Monte Carlo模擬

首先利用上述基于眾數(shù)回歸模型模擬的完全數(shù)據(jù),對響應(yīng)變量Y進(jìn)行隨機(jī)缺失,缺失率分別為5%,10%,20%,采用§3.2中的三種插補(bǔ)方法,得到插補(bǔ)后完全數(shù)據(jù),其次進(jìn)行極大似然估計,取參數(shù)的真值為β0=(0.5,?1.5,1),=2,λ0=0.5,在樣本量n為100,300的情況下分別模擬1000次.模擬結(jié)果見表4.2.

從表4.2可以得到以下結(jié)論.

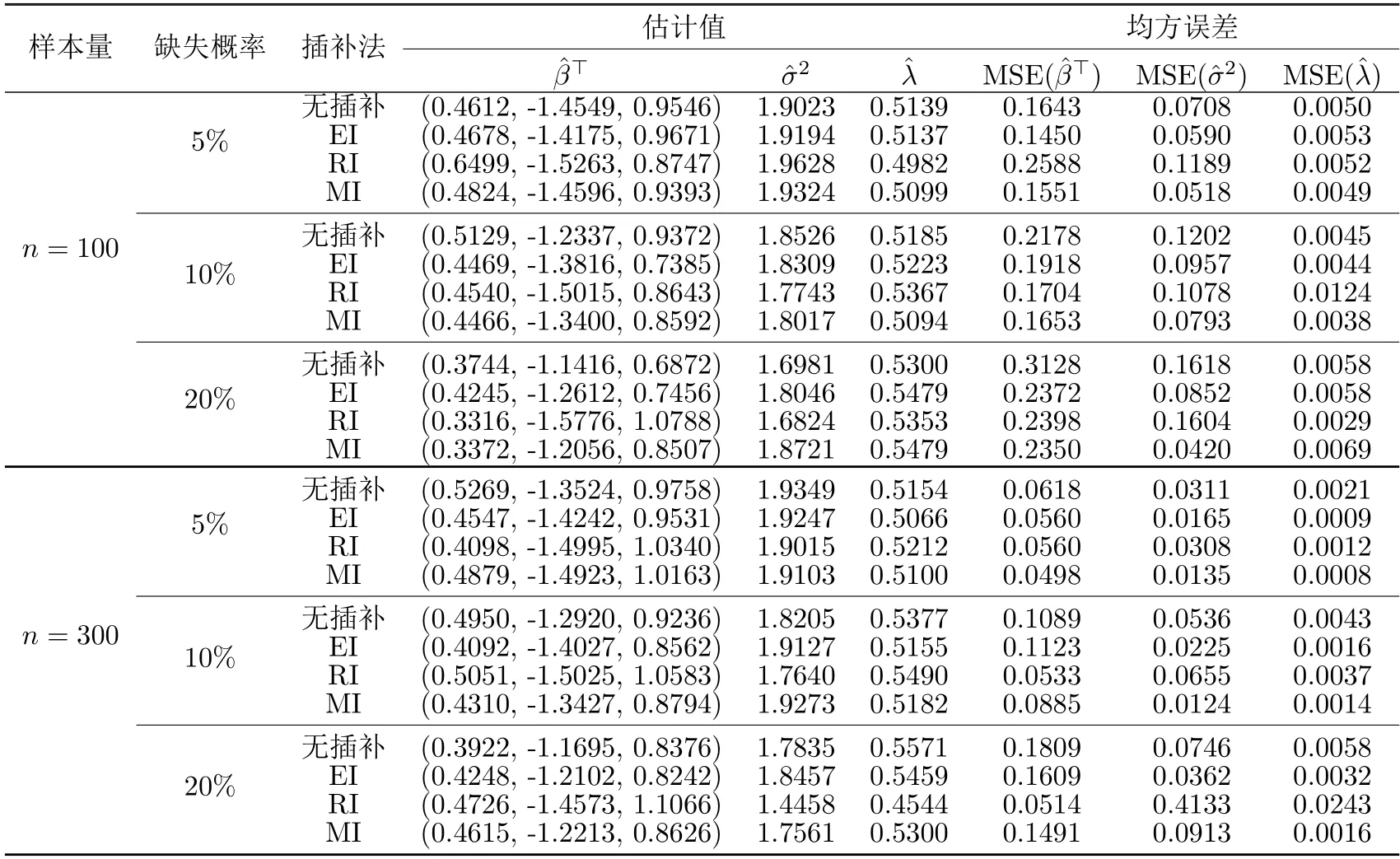
表4.2 缺失數(shù)據(jù)下眾數(shù)回歸模型的三種插補(bǔ)方法插補(bǔ)效果

(1) 隨著若樣本量逐漸增大或者缺失率逐漸減小,均值插補(bǔ),回歸插補(bǔ),眾數(shù)插補(bǔ)三種插補(bǔ)方法的估計精度越來越高,表明三種插補(bǔ)方法是可行的;

(2) 回歸插補(bǔ)在缺失率低的情況下,對偏度參數(shù)λ的估計效果較好;當(dāng)樣本量少而缺失率高時,回歸插補(bǔ)的插補(bǔ)效果很差,所得偏度參數(shù)λ與尺度參數(shù)σ2的估計值與真值偏差較大;

(3) 眾數(shù)插補(bǔ)在不同缺失率下,對尺度參數(shù)的估計效果較好.此外,眾數(shù)插補(bǔ)在缺失率低且樣本量較大的情況下,例如缺失率為5%,樣本量為300時,其回歸系數(shù)的均方誤差MSE()是三種插補(bǔ)方法中最小的.表明缺失率低且樣本量較大的情況下,眾數(shù)插補(bǔ)對回歸系數(shù)的插補(bǔ)效果比較好.

(4) 三種插補(bǔ)方法所得的估計結(jié)果與未插補(bǔ)時所得的估計結(jié)果相比,可知當(dāng)缺失率小于10%時,眾數(shù)插補(bǔ)的插補(bǔ)效果較優(yōu).

§5 實例分析

體質(zhì)指數(shù)(BMI)可簡單通過身高與體重得出.我們關(guān)注其他身體特征因素對BMI造成的影響,數(shù)據(jù)來自Cook[16]分析的BMI數(shù)據(jù),包含202名運(yùn)動員的相關(guān)體質(zhì)特征數(shù)據(jù),該數(shù)據(jù)被收錄在R軟件“sn”包中的ais數(shù)據(jù)集中,是偏正態(tài)數(shù)據(jù)的典型實例.將數(shù)據(jù)集中的體質(zhì)指數(shù)(BMI)作為響應(yīng)變量,x1-紅細(xì)胞計數(shù)(RCC),x2-白細(xì)胞計數(shù)(WCC),x3-身體肥胖百分比(Bfat),x4-去脂體重(LBM)作為解釋變量,研究這幾個解釋變量與體質(zhì)指數(shù)之間的關(guān)系.圖1繪制了數(shù)據(jù)的直方圖和概率密度函數(shù)曲線,利用R軟件估計體質(zhì)指數(shù)的偏度為=0.9465155,另外,繪制數(shù)據(jù)的正態(tài)Q-Q圖如圖2所示,散點(diǎn)存在一定程度的偏離,表明數(shù)據(jù)具有明顯的偏斜,BMI數(shù)據(jù)服從偏正態(tài)分布.

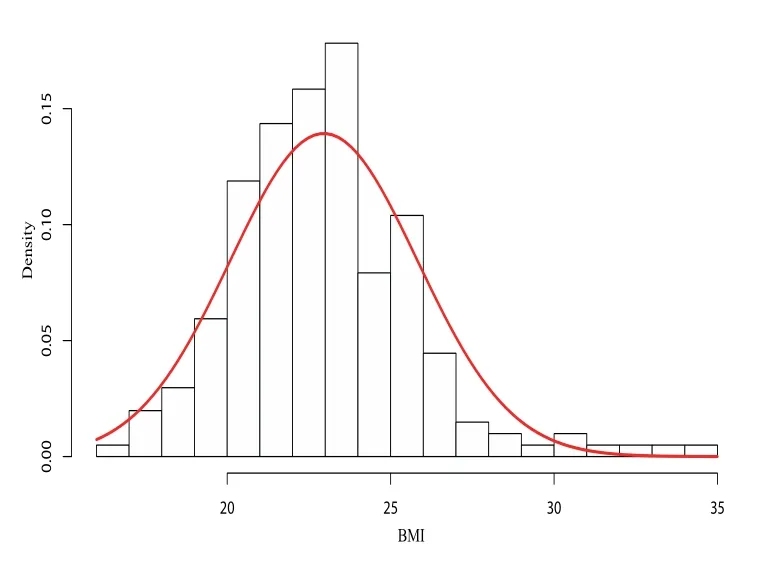
圖1 BMI密度函數(shù)擬合圖

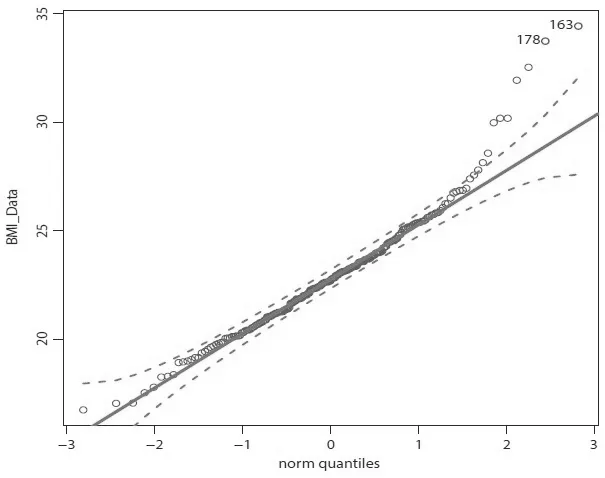
圖2 BMI數(shù)據(jù)的正態(tài)Q-Q圖

5.1 完全數(shù)據(jù)下的實例分析

利用該數(shù)據(jù)對偏正態(tài)分布下均值與眾數(shù)回歸模型做參數(shù)估計,考慮變量間關(guān)系

表5.1 均值與眾數(shù)回歸模型下完全BMI數(shù)據(jù)的參數(shù)估計

由上表可知,兩種模型參數(shù)估計存在一定差異,表明影響均值和眾數(shù)的因素不完全相同.結(jié)果顯示,眾數(shù)回歸模型的區(qū)間估計精度優(yōu)于均值回歸模型,x1-紅細(xì)胞計數(shù)與x3-身體肥胖百分比對響應(yīng)變量y-體質(zhì)指數(shù)(BMI)的均值與眾數(shù)均有影響且影響相似,而x2-白細(xì)胞計數(shù)與x4-去脂體重對應(yīng)的區(qū)間估計包含0,說明該變量不顯著;兩種回歸方法對BMI數(shù)據(jù)的尺度參數(shù)σ2和偏度參數(shù)λ的估計結(jié)果相似.從實際意義來看,完整數(shù)據(jù)下的參數(shù)估計結(jié)果表明體質(zhì)指數(shù)(BMI)基本不受x2-白細(xì)胞計數(shù)與x4-去脂體重的影響,實際研究人員在分析影響體質(zhì)指數(shù)(BMI)的因素時,可參考此結(jié)論.

5.2 缺失數(shù)據(jù)下的實例分析

體質(zhì)數(shù)據(jù)(BMI)按缺失率5%,10%,20%進(jìn)行隨機(jī)缺失,通過三種插補(bǔ)方法進(jìn)行插補(bǔ),應(yīng)用§3.2中帶有缺失的偏正態(tài)數(shù)據(jù)下的極大似然估計方法,經(jīng)過100次模擬后,得到表5.2,其中,SD為算法收斂后觀測信息陣主對角線元素開方所得的標(biāo)準(zhǔn)差,表示所有回歸系數(shù)的標(biāo)準(zhǔn)差求和.

由表5.2可得到以下結(jié)論.

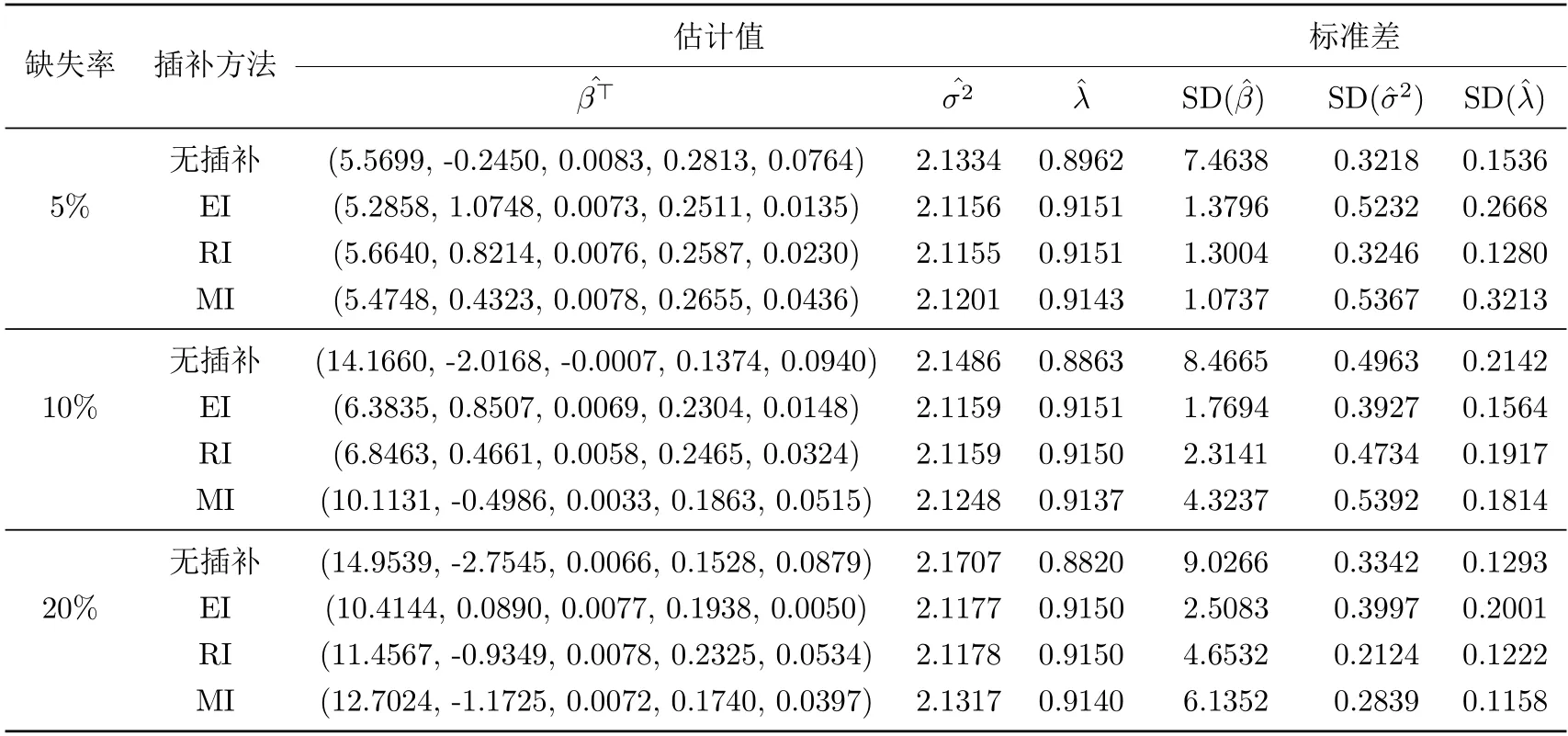
表5.2 眾數(shù)回歸模型下BMI實例結(jié)果

(1) 不同缺失率下,三種插補(bǔ)方法相較未插補(bǔ)情形,回歸系數(shù)的估計效果都得到了提升.當(dāng)缺失率從5%～20%逐漸增大時,提升效果逐漸減小.

(2) 眾數(shù)插補(bǔ)方法在缺失率低(5%)的情況下,相較均值插補(bǔ)(EI),回歸插補(bǔ)(RI)而言,對回歸系數(shù)β的估計值更接近于完全數(shù)據(jù)下的估計結(jié)果,表明眾數(shù)插補(bǔ)在低缺失率時優(yōu)于均值插補(bǔ)與回歸插補(bǔ).

(3) 不同缺失率下,均值插補(bǔ)與回歸插補(bǔ)對尺度與偏度參數(shù)的估計結(jié)果基本相同.從尺度,偏度參數(shù)的角度來看,缺失BMI數(shù)據(jù)下的估計值接近完全BMI數(shù)據(jù)下的估計值.表明眾數(shù)回歸模型下均值插補(bǔ)與回歸插補(bǔ)對尺度參數(shù)σ2,偏度參數(shù)λ的估計值更接近真實值.

§6 結(jié)論

本文基于偏正態(tài)數(shù)據(jù)構(gòu)建了眾數(shù)回歸模型,應(yīng)用高斯牛頓迭代法進(jìn)行參數(shù)的極大似然估計,并將眾數(shù)回歸模型的參數(shù)估計結(jié)果與傳統(tǒng)均值回歸模型的參數(shù)估計結(jié)果進(jìn)行了比較,模擬結(jié)果表明當(dāng)數(shù)據(jù)存在偏度時,眾數(shù)回歸模型的估計結(jié)果都優(yōu)于傳統(tǒng)均值回歸模型的估計結(jié)果.另一方面,在響應(yīng)變量隨機(jī)缺失的條件下,采用均值插補(bǔ),眾數(shù)插補(bǔ),回歸插補(bǔ)三種插補(bǔ)方法補(bǔ)全缺失數(shù)據(jù)集后,再進(jìn)行參數(shù)估計,進(jìn)而評價三種插補(bǔ)方法的插補(bǔ)效果.模擬結(jié)果表明,隨著樣本量的增大或者缺失率的減小,三種插補(bǔ)方法的估計精度都越來越高;眾數(shù)插補(bǔ)在缺失率低(5%)且樣本量較大的情況下,對回歸系數(shù)的估計結(jié)果相較其他兩種插補(bǔ)方法更優(yōu);在不同缺失率下,均值插補(bǔ)與回歸插補(bǔ)對尺度參數(shù),偏度參數(shù)的估計結(jié)果基本相同.實例分析的研究結(jié)果表明,三種插補(bǔ)方法相較未插補(bǔ)的情形,其回歸系數(shù)的估計效果都得到提升,且缺失率為10%～20%時提升效果更為明顯.