LI Yun, JIANG Kaige, ZENG Ting, CHEN Wenbin,LI Xiaoyang, LI Deyong, and ZHANG Zhiqiang

1.Beijing Spacecraft Manufacturing Co., Ltd, China Academy of Space Technology, Beijing 100094, China;

2.School of Reliability and Systems Engineering, Beihang University, Beijing 100191, China;

3.Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing 100191, China

Abstract: The planetary reducer is a common type of transmission mechanism, which can provide high transmission accuracy and has been widely used, and it is usually required with high reliability of transmission characteristics in practice.During the manufacturing and usage stages of planetary reducers, uncertainties are ubiquitous and wear is inevitable, which affect the transmission characteristics and the reliability of planetary reducers.In this paper, belief reliability modeling and analysis considering multi-uncertainties and wear are proposed for planetary reducers.Firstly, based on the functional principle and the influence of wear, the performance margin degradation model is established using the hysteresis error as the key performance parameter, where the degradation is mainly caused by the accumulated wear.After that, multi-source uncertainties are analyzed and quantified separately, including manufacturing errors,uncertainties in operational and environmental conditions, and uncertainties in performance thresholds.Finally, the belief reliability model is established based on the performance margin degradation model.A case study of a planetary reducer is applied and the reliability sensitivity analysis is implemented to show the practicability of the proposed method.The results show that the proposed method can provide some suggestions to the design and manufacturing phases of the planetary reducer.

Keywords: belief reliability, planetary reducer, performance

1.Introduction

The planetary reducer is a common type of transmission mechanism.It can provide high transmission accuracy and support high torque transmission with good stiffness and low noise [1] and has been widely used in the transmission of helicopters, automobiles, aircraft engines, etc[2].In order to make the planetary reducer operate accurately and smoothly, it is usually required to have excellent transmission characteristics in practice, where the hysteresis error is usually selected as the key performance parameter to describe the transmission characteristics of the planetary reducer [3].Large hysteresis errors can cause short-term output interruption, shocks, and unbalanced rotation, and affect the performance and reliability of the planetary reducer [4].During the long-term operation of the planetary reducer, the wear in gear pairs is inevitable [5], which increases the backlashes in the gear pairs, and results in the increase in the hysteresis error,and further, the reliability of the planetary reducer degrades.Besides, the uncertainties embedded in the manufacturing and usage processes are various and inevitable,which also affect the reliability of planetary reducers.Therefore, it is necessary to investigate the composition of the hysteresis error and conduct the reliability analysis for the planetary reducer under the consideration of multisource uncertainties and wear.

1.1 Literature review

The planetary reducer is composed of a sun gear, a ring gear, a planet carrier, and several planet gears.In the design process of planetary reducers, to avoid the gears stuck caused by the thermal expansion in the practical usage, the backlashes in gear pairs are always designed to exist in the planetary reducers [6].When the transmission direction of the input shaft of the planetary reducer changes, the backlashes in the gear pairs will cause a tiny hysteresis, i.e., the hysteresis error, in the rotation of the driven gear [7].Many scholars have studied the hysteresis error of the planetary gear from the perspective of backlashes in gear pairs.Zhu et al.[8] proposed a probability based hysteresis error model considering the backlashes in the gear pairs from gear and bearing errors for a two-stage planetary reducer.Pan et al.[9] and Wang et al.[6] focusing on a three-stage planetary reducer and a hightransmission planetary reducer, respectively, investigated the hysteresis error analysis from three aspects including manufacturing errors, assembly errors, and deformation errors, and established hysteresis error models considering the uncertainties in these errors based on probability methods.Blanche et al.and Yang et al.[10,11] presented computational models of the backlashes in the gear pairs caused by manufacturing and assembly errors.Tran et al.[12,13] studied the influence of the backlash between the cycloid disk and the pin-rollers on the hysteresis characteristics of a cycloid planetary reducer.

During the long-term operation of the planetary reducer, the wear in gear pairs is inevitable [5], which increases the backlashes in the gear pairs, and further leads to the increase of the hysteresis error of the planetary reducer.Recently, some scholars have studied the influence of wear on the backlashes in the gear pairs of planetary reducers.Wu et al.[14] modeled the increasing backlash generated by tooth surface wear and conducted a dynamic response analysis for a compound planetary gear set.Yuksel et al.[15] and Bajpai et al.[16] employed a finite elements-based gear contact mechanics model in conjunction with Archard’s wear model to study the wear of contacting tooth surfaces in a planetary reducer.Kahraman et al.[17] proposed a dynamic planetary gear wear model considering the influence of worn surface profiles under dynamic conditions.Tunalioglu et al.[18]conducted Archard model based theoretical and experimental investigation of wear focusing on the internal gear of a planetary reducer.However, most of the existing researches focused on the modeling and analysis of the increase in the backlashes caused by wear other than the influence of wear on hysteresis errors and seldom considered the influence of uncertainties.

Reliability is an important parameter of planetary reducers, which describes the capability of planetary reducers to perform a specified function for a given period of time under stated operating conditions.Recently, some scholars have conducted reliability analysis on planetary reducers.Zhou et al.[19] conducted dynamic reliability analysis by evaluating the probability of dynamic contact stress exceeding the material strength considering the uncertainties in manufacturing errors and contact stresses.Liang et al.[20] and Shang et al.[21] conducted reliability analysis focusing on contact fatigue and bending fatigue of a planetary reducer.Li et al.[22] carried out a bending fatigue test and conducted reliability analysis for a helicopter planetary reducer considering unequal load sharing.Gao et al.[23], and Zhou [24] conducted strength analysis and implemented strength reliability analysis for planetary reducers considering the strength degradation of gears.

1.2 Current problems

Though existing studies have contributed a lot to the hysteresis error of planetary reducers, there are still some problems:

(i) The degradation of hysteresis error caused by wear is seldom studied since current studies mainly aim at the modeling of hysteresis error and the influence of wear on the backlashes in the gear pairs.

(ii) The uncertainties from the manufacturing to usage processes are not fully considered in current researches,such as the manufacturing errors, the uncertainties in wear rate, and the uncertainties in the performance threshold.

(iii) Current studies on reliability mainly focus on the strength failures of planetary reducers other than the degradation of hysteresis errors.

1.3 Contributions

Taking the planetary reducer as the research object, we focus on the hysteresis error as its key performance parameter to describe its transmission performance, and propose a belief reliability modeling and analysis method with the consideration of the wear effect and multi-source uncertainties in the manufacturing and usage processes.The following aspects are highlighted:

(i) The performance margin degradation model is constructed based on the structural relationships of the components in the planetary reducer, where the degradation is mainly caused by the accumulated wear;

(ii) Multi-source uncertainties are considered and quantified one by one, including manufacturing errors,the uncertainties in operational and environmental conditions, and the uncertainties in the performance threshold;

(iii) Under the consideration of multi-source uncertainties, the belief reliability model is given based on the performance margin degradation model by measuring the probability of the performance margin larger than 0.

1.4 Organization and framework

The framework of the proposed belief reliability modeling and analysis method considering the wear effect and multi-source uncertainties is shown in Fig.1.Firstly, the function/performance analysis of the planetary reducer is conducted in Section 2, and the performance margin model for the hysteresis error is constructed.Additionally, considering wear is the main degradation mechanism, the wear process is modeled, and further, the performance margin degradation model is established by combining the performance margin model and the wear model.Then, in Section 3, the multi-source uncertainty analysis and qualification for the performance margin degradation model are conducted, where three main sources of uncertainties are considered: manufacturing errors, the uncertainties in operational and environmental conditions, and the uncertainties in the performance threshold.After that, the belief reliability model considering the wear effect and multi-source uncertainties is constructed in Section 4.Section 5 presents a numerical study of a planetary reducer and implements the reliability sensitivity analysis.Finally, Section 6 concludes the work and provides some future research directions.

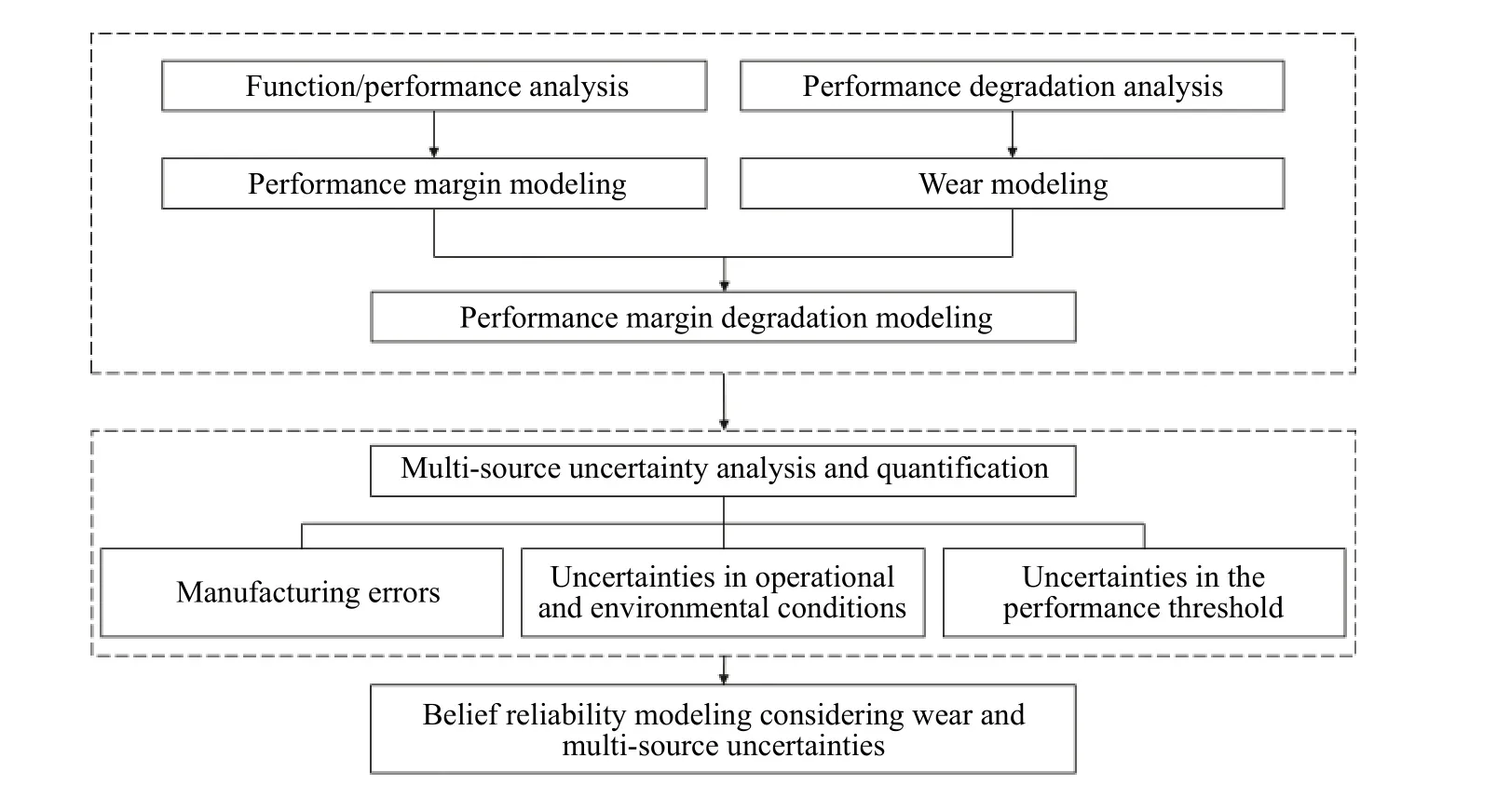
Fig.1 Framework of the belief reliability modeling and analysis method for the planetary reducer considering the wear effect and multisource uncertainties

2.Performance margin degradation modeling for the planetary reducer

2.1 Introduction to the planetary reducer

The planetary reducer is a common type of transmission mechanism which can provide high transmission accuracy and support high torque transmission with good stiffness and low noise [1], and has been widely used.The planetary reducer to be studied is an NGW (N represents the internal gear pair, G represents a common gear engaged with two central gears simultaneously and W represents the external gear pair) type planetary reducer,which is composed of a sun geara, a fixed ring gearb, a planet carrierH, and three planet gearscl(l=1, 2, 3), as shown in Fig.2.Two types of gear pairs are contained in the planetary reducer: the external gear pairacland the ring gear pairbcl.

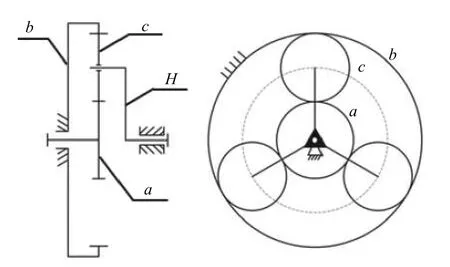
Fig.2 Structure model of an NGW type planetary reducer

During the operation of the planetary reducer, the input power drives the sun gear to rotate, and further drives the surrounding planetary gears which are housed in a rotating planetary carrier.Then the output shaft connected with the planetary carrier connects rotates to output the torque and rotating speed.

2.2 Performance margin modeling

In the design process of planetary reducers, to avoid the gears stuck caused by thermal expansion in practical usage, the backlashes in gear pairs are always designed to exist in planetary reducers [6].When the transmission direction of the input shaft of the planetary reducer changes, the backlashes in the gear pairs will cause a tiny hysteresis, i.e., the hysteresis error, in the rotation of a driven gear [7].Large hysteresis errors can cause shortterm output interruption, shocks, and unbalanced rotation,and affect the performance of the planetary reducer [4].Consequently, the requirements for hysteresis errors are usually very strict in practice.Therefore, the hysteresis error is chosen as the key performance parameter to describe the transmission characteristics of the planetary reducer.

According to the structural relationships of the components in the planetary reducer shown in Fig.3, the rotation angles of the sun gear and the planet gear from the moment that the sun gear begins to change its rotation direction to the moment that the planet carrier rotates are Δθaand Δθc, respectively.Δθaand Δθcalso represent the angle changes of the sun gear and the planet gear when the planetary reducer overcomes their circumferential backlashes when changing the rotation direction, respectively.

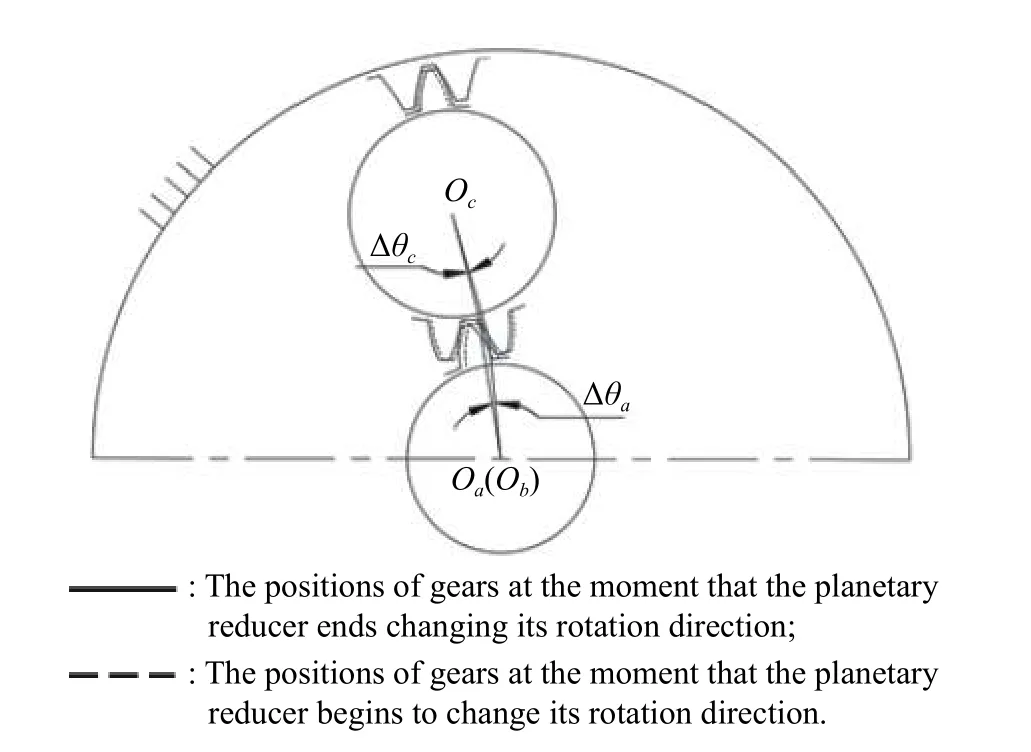
Fig.3 Angle changes of the sun gear and the planet gear when the planetary reducer changes its rotation direction

Based on Fig.3, the following relationships can be obtained:

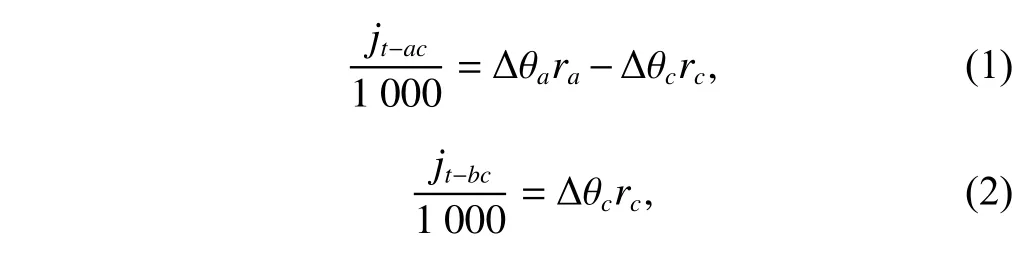
wherejt?kdenotes the circumferential backlash in the gear pairk(k=ac,bc), andridenotes the reference radius of the geari(i=a,b,c).

By solving (1) and (2), we have

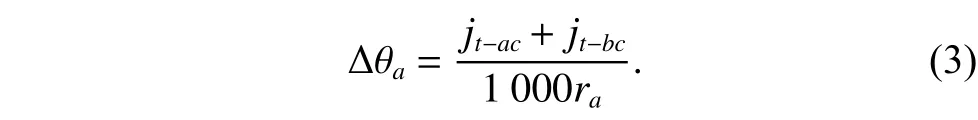
The hysteresis error of the planetary reducer is the lag in the rotation angle of the output shaft when the rotation direction of the input shaft is changed [4], which can be calculated as

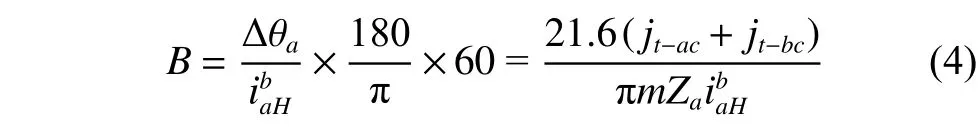
whereBdenotes the hysteresis error of the planetary reducer,denotes the transmission ratio of the planetary reducer,mdenotes the module of the gears, andZadenotes the number of the teeth of the sun gear.

Assume that the hysteresis error threshold isC, and the hysteresis error marginMis

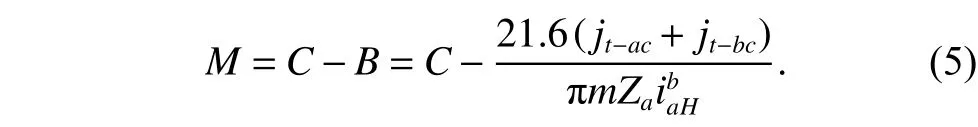
The planetary reducer is reliable wheneverM>0.

2.3 Wear modeling

During the long-term operation of the planetary reducer,the wear in gear pairs is inevitable [5], which increases the backlashes in the gear pairs, and further leads to the degradation in the hysteresis error.In general, the wear process consists of three typical stages: running-in wear stage, stable wear stage, and severe wear stage [25],shown in Fig.4.

Fig.4 Typical wear stages

Before putting the planetary reducer into use, it usually experiences the running-in wear stage to identify and eliminate units with infant mortality [26].Thus, it can be considered that the planetary reducer is in the stable wear stage with a constant wear rate in the usage stage, i.e.,

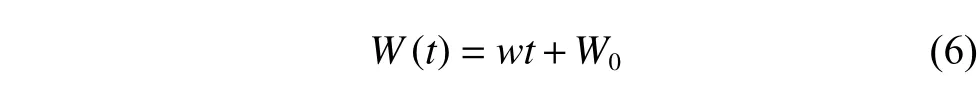
whereW(t) denotes the wear amount at the timet,wdenotes the wearing rate in the meshing direction, andW0denotes the wear amount of the running-in wear stage.

Since the wear amount of the running-in wear stage is rather small, to be simplified,W0is neglected in this paper.Then, the circumferential backlash caused by wear is

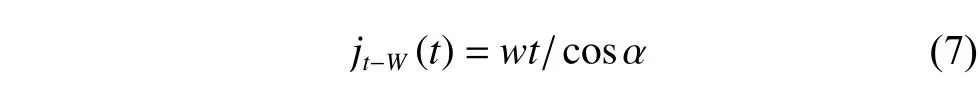
wherejt?W(t)denotes the circumferential backlash caused by the wear at the timet, andσdenotes the working pressure angle.

2.4 Performance margin degradation modeling

Considering the effect of the accumulated wear damage,the hysteresis errorBof the planetary reducer in (4) can be rewritten as

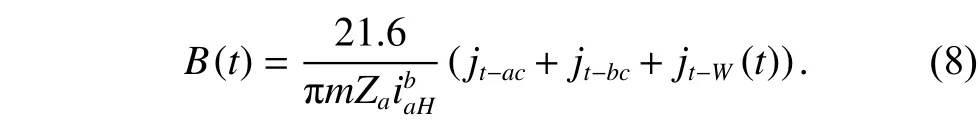
Then the performance margin degradation model can be constructed as

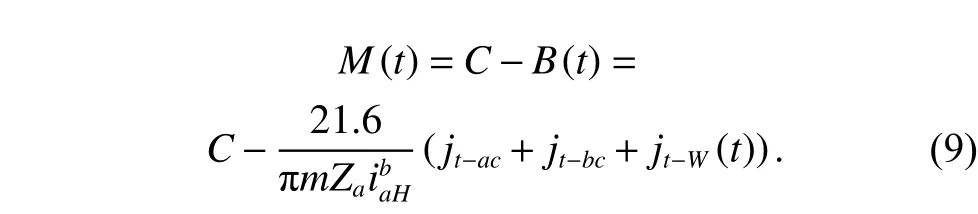
The above performance margin degradation model (9)shows the degradation law of the performance margin with time caused by wear, and the planetary reducer is reliable wheneverM(t)>0.

3.Multi-source uncertainty analysis and quantification

In the manufacturing and usage processes, uncertainties are ubiquitous and influence the hysteresis error of the planetary reducer.Therefore, it is of great significance to figure out the uncertainty sources of the planetary reducer and quantify them one by one precisely.The uncertainties are primarily from three sources: the uncertainties in manufacturing errors, the uncertainties in operational and environmental conditions, and the uncertainties in the performance threshold.In this section, these uncertainties are analyzed and quantified separately.

3.1 Manufacturing errors

The manufacturing errors are inevitable in the manufacturing process, which can affect the circumferential backlashes in the gear pairs, and further, affect the hysteresis error of the planetary reducer.In general, considering the existence of uncertainties, the manufacturing errors of components are regarded as random variables [27].As for the planetary reducer, the sources of circumferential backlashes caused by manufacturing errors can be divided as follows:

(i) the dimension errors between the actual sizes and the theoretical sizes of components due to the inherent errors in the manufacturing machines, including the manufacturing errors of gear, i.e., the circumferential backlashesjtEM?iandjteg?icaused by the tooth thickness deviation and eccentricity error of the geari, respectively; the manufacturing errors of bearing, i.e., the circumferential backlashesjtkeaandjtΔrcaused by the radial circular runout and the radial internal clearance of bearing, respectively; the circumferential backlashjtΔrcpcaused by the clearance between the hole of the sun gear and the input shaft.

(ii) the variation in the material physical properties during the fabrication of materials, including the circumferential backlashjtT?kin the gear pairk, caused by the thermal expansion of materials under different environmental temperature conditions.

By accumulating all circumferential backlashes caused by the manufacturing errors, the circumferential backlashesjt?acandjt?bcin the gear pairsacandbcin (10) are

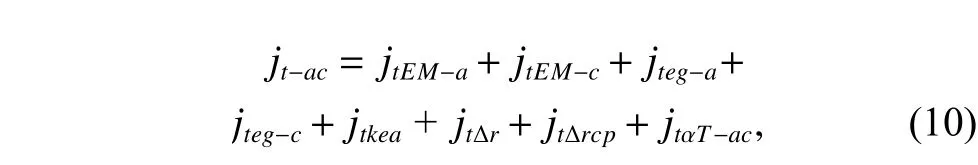
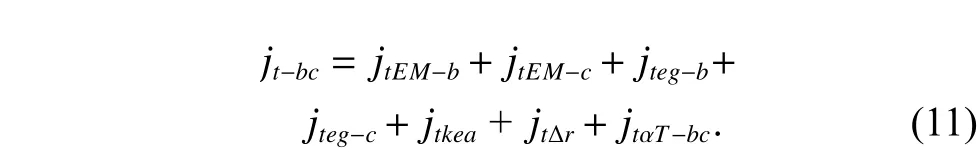
In the manufacturing process of products, in order to control dimension errors, a standardized tolerance system is used, and the manufacturing tolerances of the product are marked on the product as part of the manufacturing information, including the gear tolerance, the bearing tolerance, and the engineering fit between the shaft and the hole.The manufacturing information is referred to in this paper to quantify the uncertainties in its manufacturing process.

3.1.1 Manufacturing errors of gears

(i) The circumferential backlash caused by the tooth thickness deviation

Tooth thickness deviation is the difference between the actual tooth thickness and the nominal tooth thickness.ISO 1 328-1 [28] and ISO 1 328-2 [29] give the maximum and the minimum tooth thickness deviationsEsns?iandEsni?iof the gearifor a certain tolerance grade of gear, respectively.For the backlash caused by the tooth thickness deviation of the sun gear, we have

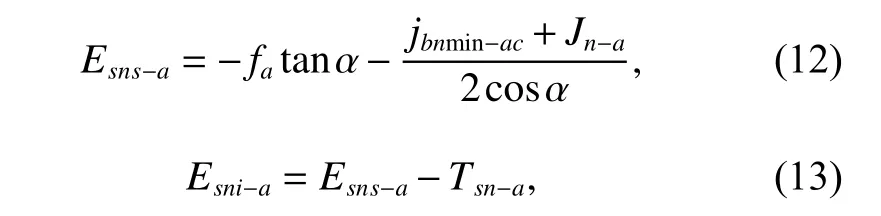
wherefadenotes the deviation of the center distance,jbnmin?acdenotes the minimum meshing clearance of the gear pairac,Jn?adenotes the compensation of the clearance of the sun gear due to the manufacturing and assembly errors, andTsn?adenotes the tooth thickness tolerance of the sun gear.

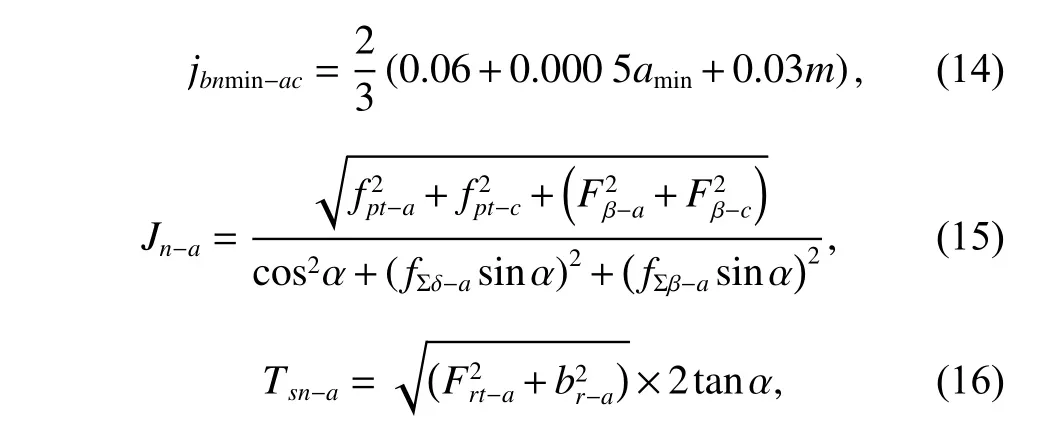
whereamindenotes the minimum center distance,fpt?adenotes the single pitch deviation of the sun gear,Fβ?idenotes the total helix deviation of the sun gear,fΣβ?idenotes the parallelism deviation of the axis of the sun gear in the vertical plane,fΣδ?idenotes the parallelism deviation of the axis of the sun gear in the axis plane,br?idenotes the tolerance of the radial tool feed of the sun gear,andFrt?idenotes the tolerance of the radial circular runout of the sun gear.

It is assumed that the tooth thickness deviation of the sun gearEsn?ais a random variable following a normal distribution, then its mean value and standard variance can be computed according to the 6-sigma limit in mechanical design [30]

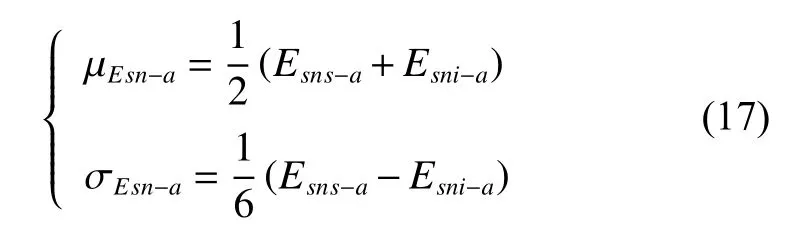
whereμxandσxindicate respectively the mean and the standard deviations of the random variablex.

The circumferential backlashjtEM?acaused by the tooth thickness deviation of the sun gear is

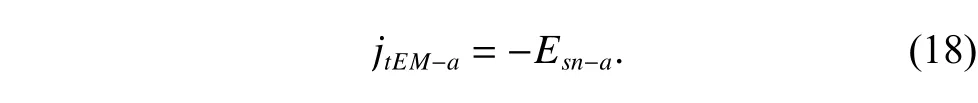
Then we can obtain thatjtEM?ais also a random variable following a normal distribution:

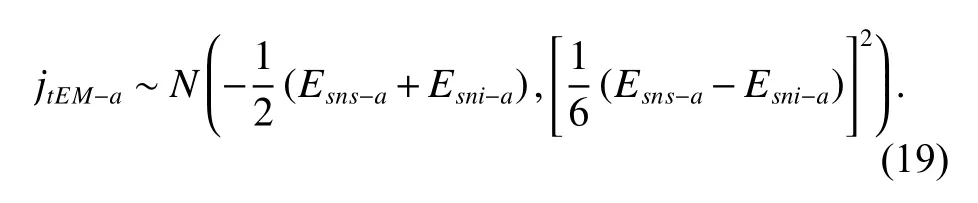
Similarly, the distributions of the circumferential backlashjtEM?bandjtEM?ccan be obtained as

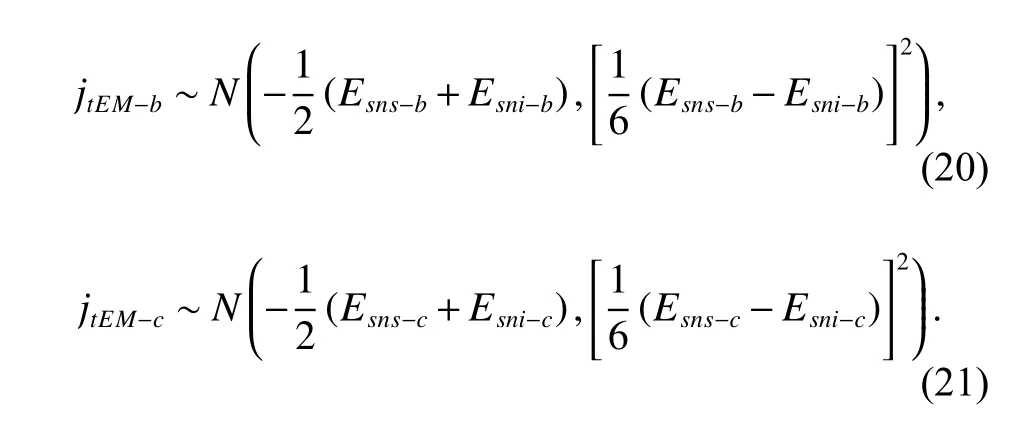
(ii) The circumferential backlash caused by the eccentricity error of the gear

The eccentricity erroreg?iof the geariis the difference between the actual machining center and the theoretical center, which consists of the components in two directions: the tangential componentegt?iand the radial componentegr?i.

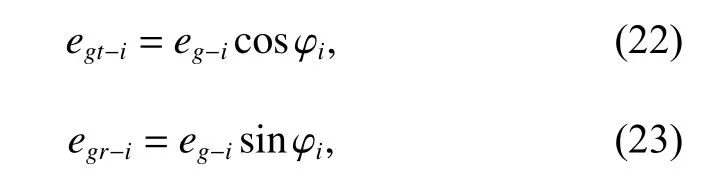
whereφiis the phase angle of the eccentricity error of the geari.

For the planet gear, when it meshes with the sun gear and the ring gear, the tangential component of its eccentricity error decreases the circumferential backlash on one side of the planet gear but increases the circumferential backlash equally on the other side of the gear.Therefore,the tangential component of its eccentricity error does not affect the overall values of circumferential backlashes.Additionally, the radial component of its eccentricity error increases (or decreases) the circumferential backlash of the gear pairacbut meanwhile decreases (or increases)the circumferential backlash of the gear pairbcby an equal amount.Therefore, the radial component of its eccentricity error does not affect the overall values of circumferential backlashes as well.Hence, the influences of eccentricity errors of planetary gears on the circumferential backlashes can be ignored.

Similarly, for the sun gear and the ring gear, the tangential components of their eccentricity errors do not affect the circumferential backlashes since the circumferential backlashes of the gear pairs increase on one side and decrease on the other by an equal amount.Therefore, influences of the tangential components of eccentricity errors of the sun gear and the ring gear on the circumferential backlashes can be ignored.Then, the circumferential backlash caused by the eccentricity error is equal to the circumferential backlash caused by its radial components.For the sun gear, the circumferential backlash caused by the eccentricity error is

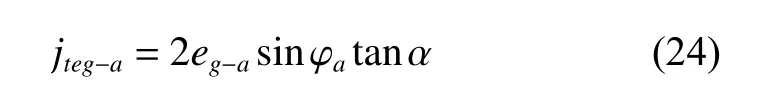
whereeg?acan be evaluated by the radial circular run-outFr?aof the sun gear [4]

ISO 1 328-2 [29] gives the tolerance of the radial circular run-outFr?iof the gearifor a certain tolerance grade,denoted asFrt?i.

It is assumed thatFr?ais a random variable following a normal distribution, then according to the 6-sigma limit in mechanical design [30], its mean value and standard variance can be computed by

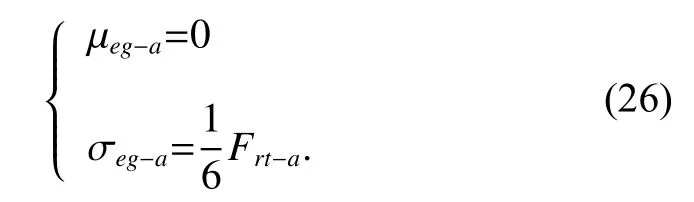
Then,eg?ais also a random variable satisfying

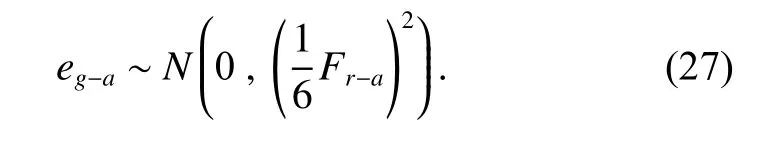
φais the phase angle of the eccentricity error of the sun geara, which can be regarded to be randomly distributed in the interval [0,2π].Thusφais assumed as a random variable following the uniform distribution

Similarly, for the ring gearb, we have

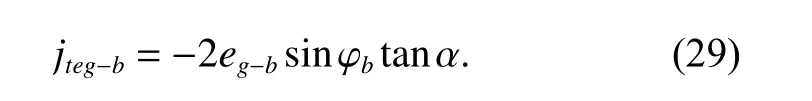
And the distributions ofeg?bandφbare

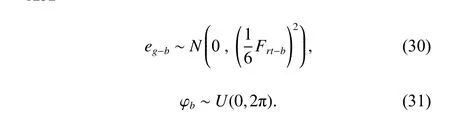
3.1.2 Manufacturing errors of bearing

(i) The circumferential backlash caused by the radial circular run-out of bearing

The planet gear is installed on its bearing and the radial circle run-outKeaof bearing influences the clearances in the gear pairs.ISO 492 [31] gives the limit deviation ofKeafor a certain tolerance class of bearing, denoted astKea.Again, the 6-sigma limit [30] is employed and the mean value and standard variance ofKeaare

The circumferential backlashjtkeacaused by the radial circular run-out of bearing is

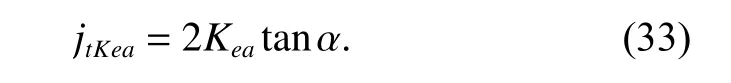
Then we can obtain thatjtkeais also a random variable following a normal distribution

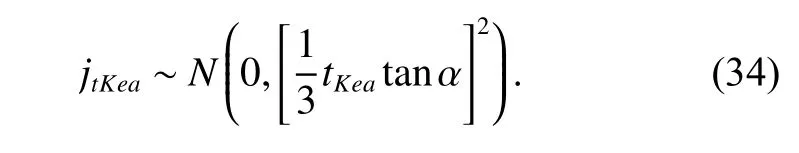
(ii) The circumferential backlash caused by radial internal clearance of bearing

The radial internal clearance Δrof bearing is the clearance between the rollers and the bearing shell.When the bearing is stressed, its radial interval clearance will be compressed, which affects the clearances in the gear pairs.ISO 5 753-1 [32] gives the maximum and minimum clearance values of radial internal clearance of bearing for a certain clearance class of bearing, denoted as Δrmaxand Δrmin, respectively.It is assumed that Δris a random variable following a normal distribution.Again, according to the 6-sigma limit [30], the mean value and standard variance of Δrar e

The circumferential backlashjtΔrcaused by the radial internal clearance of bearing is

ThenjtΔris also a random variable following a normal distribution:

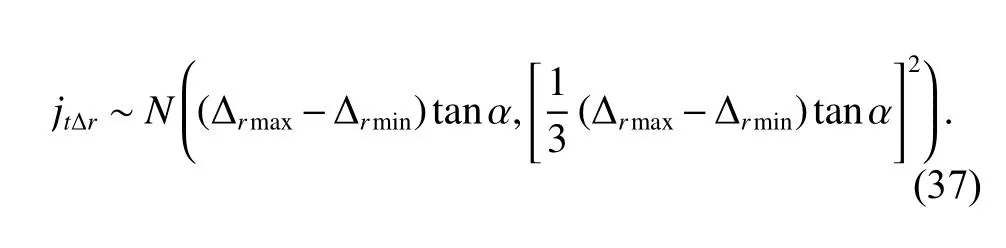
3.1.3 Circumferential backlash caused by the clearance between the hole of the sun gear and the input shaft

The engineering fit Δrcpbetween the hole of the sun gear and the input shaft is clearance fit, which affects the clearance in the gear pairs.Li et al.[33] considered that the clearance between the hole of the sun gear and the input shaft is a random variable and provided a probability distribution to describe the uncertainties in the clearance

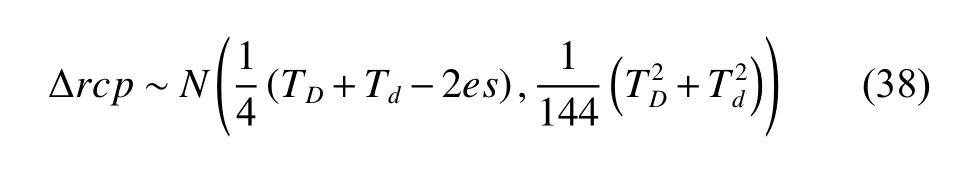
whereTDdenotes the tolerance of the hole,Tddenotes the tolerance of the shaft, andesdenotes the upper deviation for the shaft diameter.And their numerical values can be obtained from ISO 286-2 [34] under a given engineering fit.

The circumferential backlashjtΔrcpin gear pairaccaused by the clearance between the hole of the sun gear and the input shaft is

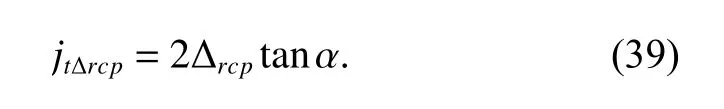
Then,jtΔrcpis also a random variable following a normal distribution

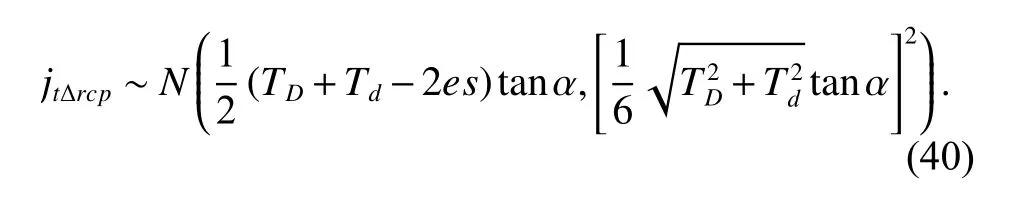
3.1.4 Circumferential backlash caused by the thermal expansion of materials

The change in temperature causes the linear thermal expansion of components, and further causes the change in the clearances in gear pairs under different environmental temperature.The circumferential backlashes in the gear pairsacandbccaused by the thermal expansion of materials are

whereαT?iandαT?Hdenote the coefficients of linear thermal expansion of the geariand the planet carrier,TandT0denote the environmental temperature and the temperature under normal conditions, andrHdenotes the radius of the planet carrier.

Due to the variation in the material physical properties during the fabrication of materials [35], the coefficient of linear thermal expansionαT?aof the sun gearais regarded as a random variable [36]

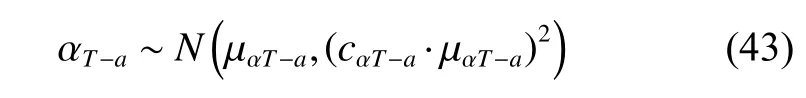
wherecxdenotes the coefficient of variance of the random variablex.

Similarly, the coefficient of linear thermal expansionαT?b,αT?c, andαT?Hare also random variables, and their distributions are

3.1.5 Distributions of the manufacturing errors

As analyzed above, the uncertainty quantification results of the manufacturing errors can be summarized in Table 1.

Table 1 Distributions of the manufacturing errors

3.2 Uncertainties in operational and environmental conditions

In practice, the operational and environmental conditions impossibly remain constants [37].During the operation of the planetary reducer, on one hand, the uncertainties are embedded in the environmental temperature; on the other hand, the rotation speed and load of the planetary reducer are usually not constants, which causes the fluctuation in the wear process [38] and is reflected by the uncertainties in the wear rate.

As analyzed above, as for the case of the planetary reducer, the uncertainties in temperature affects the circumferential backlashes caused by the thermal expansion according to (41) and (42), and the uncertainties in the wear rate affect the circumferential backlashes caused by wear according to (7).Therefore, the temperature and the wear rate are regarded as random variables following normal distributions, as shown in Table 2.To quantify the uncertainties in temperature, the actual monitoring data of operational and environmental conditions of the planetary reducer can be used; to quantify the uncertainties in the wear rate, the testing data from the wear test of the planetary reducer can be used.

Table 2 Distributions of temperature and wear rate

3.3 Uncertainties in the performance threshold

The performance thresholds characterize the boundaries conditions for the system to perform specified functions.The hysteresis error is the key parameter to describe the transmission performance of planetary reducers in this paper, and it can cause short-time output interruption, impact, and motion imbalance.Therefore, in practical applications, the hysteresis error is often strictly required to reduce its impact on the transmission performance of planetary reducers.Hence, GB/T 11281 [39] gives the error level requirements for the hysteresis error of planetary reducers and specifies the upper limitCUand lower limitCLof the allowable error for the performance threshold at each error level.Thus, we consider the hysteresis error thresholdCis a random variable following a uniform distribution, as shown in Table 3.

Table 3 Distribution of the performance threshold

4.Belief reliability modeling for the planetary reducer

Based on the analysis and quantification results for multisource uncertainties in Section 4, many parameters in the performance margin degradation model (9) are random variables.Then the performance degradation margin is also a random variable, represented by.

Kang [40] proposed belief reliability for reliability modeling based on performance margins.Then, the belief reliability model for the hysteresis error is

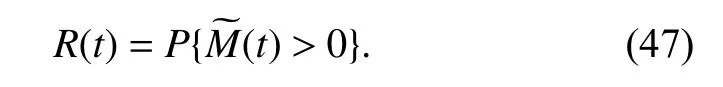
R(t) is the reliability after a period of timet, which considers the performance margin under the effect of wear and multi-source uncertainties in practical usage.Since the explicit formula of (47) is impossibly given, the Monte Carlo method is applied to compute the reliability for the planetary reducer; and its pseudocode is shown in Algorithm 1.

Algorithm 1Monte Carlo method for computing the belief reliability

Initialization:operation timetandq=0.

1.Forp=1 toNdo

2.Generate a random number for each random variable according to its corresponding distribution in Sec-.tion 4 and obtainxp=(jtEM?a,jtEM?b,jtEM?cw,jtEM?cn,eg?a,eg?b,φa,φb,jtKea?c,jtΔr,jtΔrcp,αT?a,αT?b,αT?c,αT?H,T,w,C)

3.Calculate the performance marginby (9) usingxp.

5.q=q+1.

6.Else

7.q=q.

8.End for

9.CalculateR(t)=q/N.

5.Numerical study

5.1 Parameter determination

For the case of the planetary reducer, we adopt an NGW type planetary reducer from some company, which is served as a critical component in a space drive mechanism.The physical parameters of the planetary reducer are shown in Table 4.

Table 4 Physical parameters of the planetary reducer

The tolerances of the sun gear, ring gear, and planet gear are IT6, the bearing type is 628/4/P4, and the engineering fit between the input shaft and the hole of the sun gear is H7/h6.

The material of all components of the planetary reducer is 9Cr18.According to Section 3.1.4, the coefficient of linear thermal expansion is regarded as a random variable following a normal distribution where the mean is 10.6×10?6°C?1referring to [41], and the coefficient of variation is set to be 0.1.

The planetary reducer works at 25 °C with the rotation speed of 900?1 200 rpm, and load of 80?120 Nm.According to Section 3.2, the temperature and the wear rate are regarded as random variables following independent normal distributions, where the means of the temperature and the wear rate are 25 °C and 8.3×10?3μm·h?1[42], respectively, and the coefficients of variation of the temperature and the wear rate are set to be 0.1.

The error grade of the given planetary reducer is Grade G.According to Section 3.3, the distribution of the hysteresis error threshold is set to beC~U(40,90).

5.2 Belief reliability analysis

According to Sections 2?4 and parameters in Section 5.1,the hysteresis error of the planetary reducer and its margin can be obtained, shown in Fig.5.

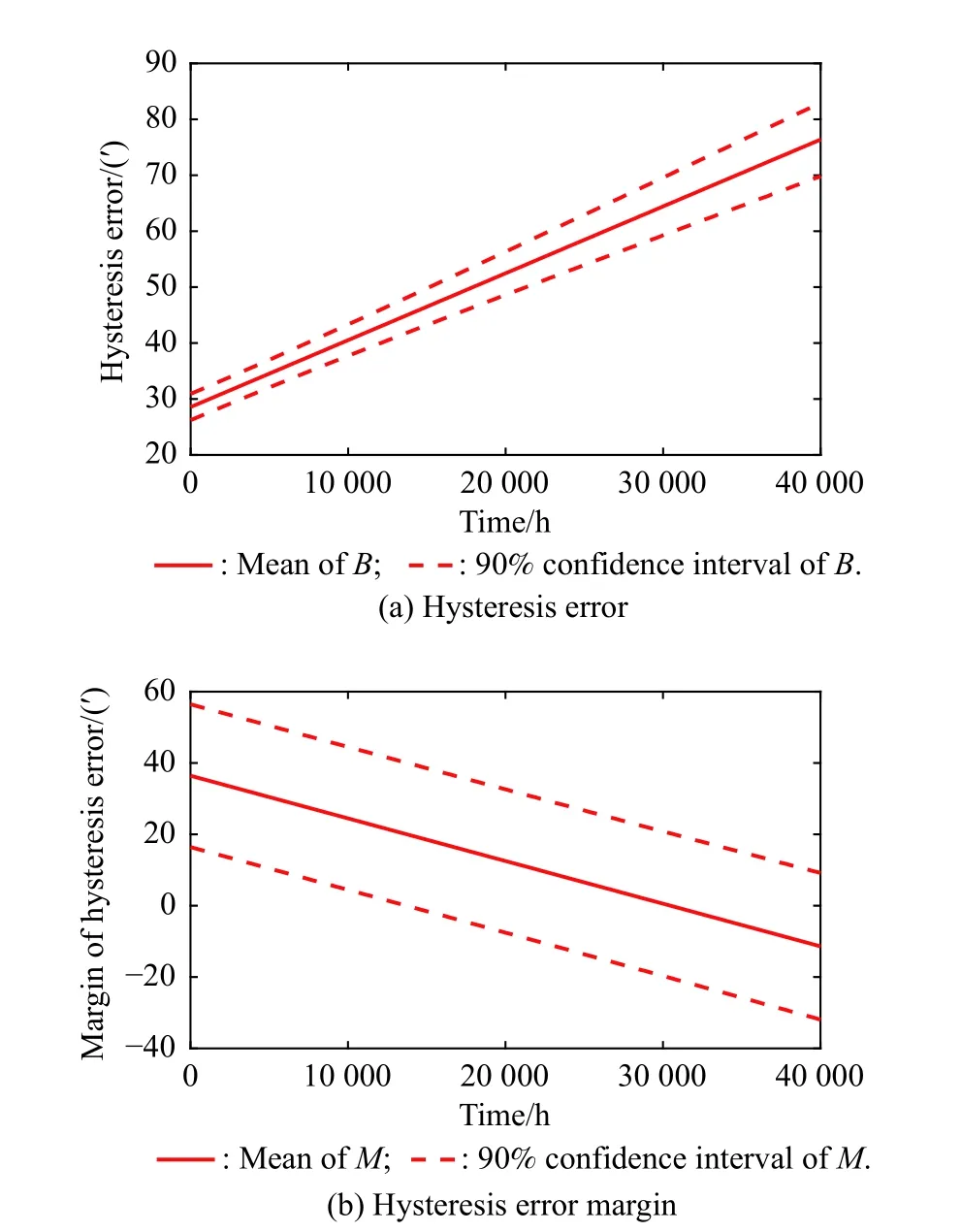
Fig.5 Hysteresis error and its margin of the planetary reducer

As shown in Fig.5, we can obtain the following results:

(i) From Fig.5 (a), the hysteresis error of the planetary reducer increases with operation time, which indicates the degradation of hysteresis error; corresponding to the result in Fig.5 (b), the hysteresis error margin decreases with time.

(ii) The hysteresis error of the planetary reducer is not 0 at the initial time, which indicates that the planetary reducer has the inherent uncertainties because of manufacturing errors.

(iii) The width between 10% and 90% percentiles of the hysteresis error and its margin increase with time,which reveals an increase in the uncertainties of the hysteresis error and its hysteresis error margin with time.

Then the belief reliability of the planetary reducer can be computed, shown in Fig.6.When the reliability is 0.9,the operation time of the planetary reducer is 13 500 h.

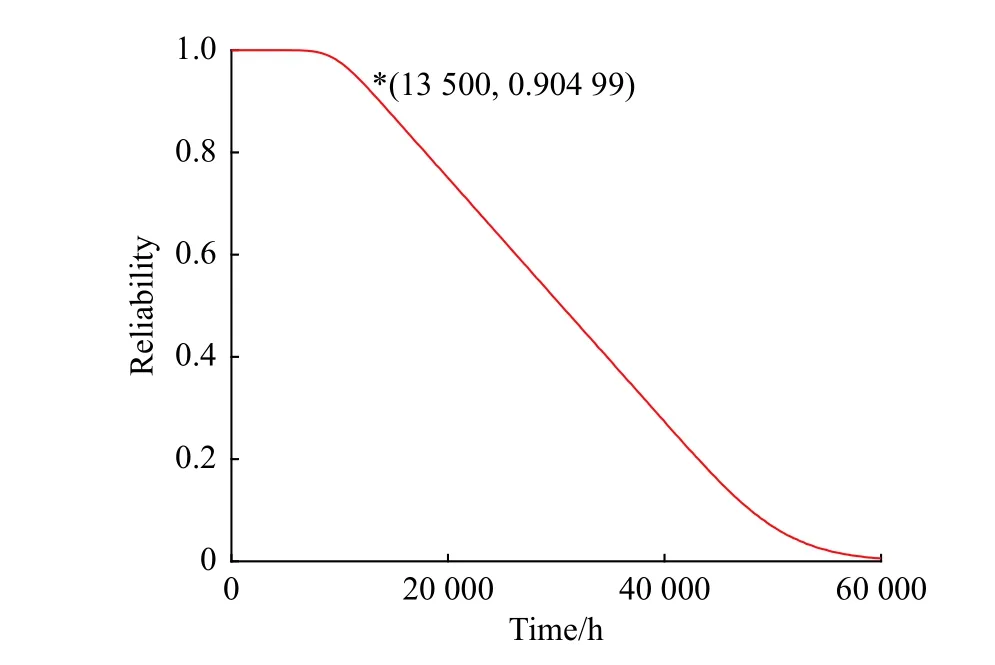
Fig.6 Reliability of the planetary reducer

5.3 Reliability sensitivity analysis for the design of the planetary reducer

Reliability designs are supposed to be conducted in the design process of products, which can ensure that the product performs the specified functions with high reliability.In the manufacturing and usage processes of planetary reducers, the uncertainties are ubiquitous and result in the uncertainty in the hysteresis error, further, they influence the reliability of planetary reducers.Therefore, in the reliability design process of planetary reducers, the influence of multi-source uncertainties on the reliability of the planetary reducer should be considered comprehensively.Herein, in this section, a comprehensive reliability sensitivity analysis for the design of the planetary reducer is carried out.

5.3.1 Reliability sensitivity analysis for manufacturing errors

For the case of the planetary reducer, the manufacturing errors are reflected in the gear tolerances, the bearing tolerance, the engineering fit between the input shaft and the hole of the sun gear, and the coefficient of variance for the coefficient of linear thermal expansion.In this section, we explore how the variations of these parameters influence the hysteresis error margin and its reliability.

(i) Gear tolerance

The planetary reducer contains three types of gears: the sun gear, the ring gear, and the planet gear.For the manufacturing tolerance of each gear, we select the gear tolerance as IT5, IT6 (original tolerance) and IT7 while keeping other parameters unchanged, and calculate the hysteresis error margin and its reliability, respectively, shown in Fig.7.

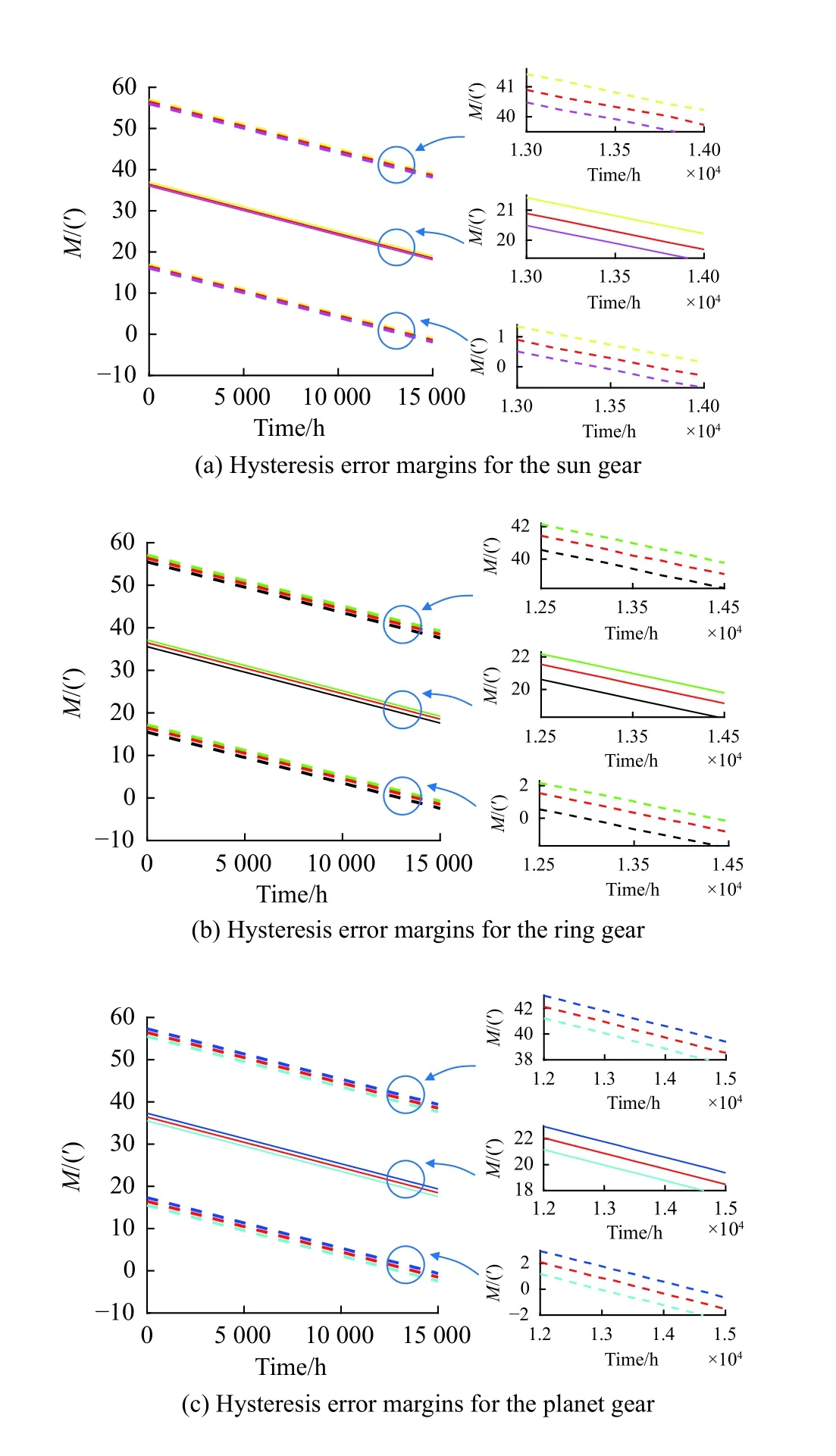
Fig.7 Hysteresis error margins and reliability under different gear tolerances

From Fig.7, the following results can be obtained:

i) From Fig.7(a) to Fig.7(c), the bigger the tolerance is, the smaller the hysteresis error margin is.It can be seen that the curve of hysteresis error margin shifts up and down with the change of gear tolerance, which indicates that the change of gear tolerance will not affect the degradation of the hysteresis error margin.

ii) Corresponding to the result above, from Fig.7(d),the bigger the tolerance is, the lower the reliability will be, and the reliability curve shifts left and right with the change of gear tolerance.

iii) According to the distance between the changed curve and the original curve (the red curve), the influences of different gear tolerances on the hysteresis error margin and its reliability can be sorted: the planet gear >the ring gear > the sun gear.

(ii) Bearing tolerance

According to Section 3.1.2, the manufacturing errors in bearing include the radial circular run-out and radial internal clearance of bearing, which can be evaluated by using the tolerance class and the clearance class, respectively.To explore the influence of manufacturing errors in bearing on the performance margin and reliability, we select the tolerance classes as IT2, IT4 (original tolerance)and IT5, and the clearance classes as Group 2, GroupN(original clearance), and Group 3 while keeping other parameters unchanged, respectively.The results of the hysteresis error margin and reliability are shown in Fig.8 and Fig.9.

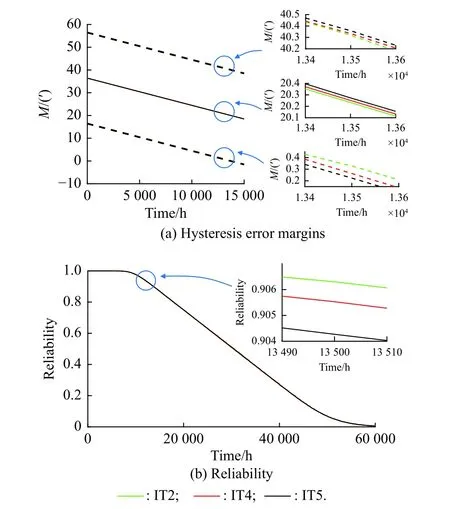
Fig.8 Hysteresis error margins and reliability under different bearing tolerance classes

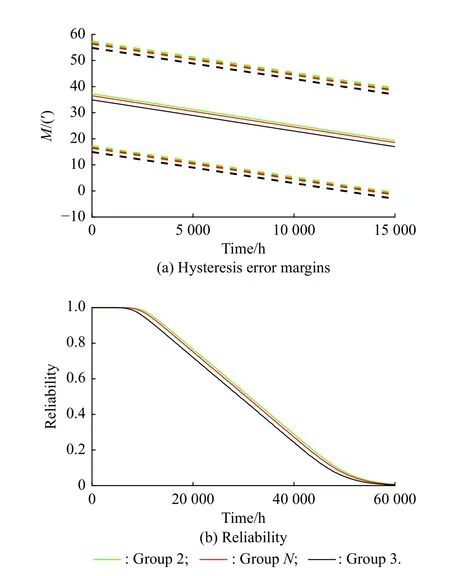
Fig.9 Hysteresis error margins and reliability under different bearing clearance classes

From Fig.8, the hysteresis error margin and reliability hardly change under different bearing tolerances.From Fig.9, the bigger the tolerance of radial internal clearance is, the smaller the hysteresis error margin and reliability are.

(iii) Clearance fit

For the clearance fit between the hole of the sun gear and the input shaft, H6/h5, H7/h6 (original clearance fit),and H8/h7 are selected while keeping other parameters unchanged.Then we explore how these varied clearance fits influence the hysteresis error margin and reliability,and the results are shown in Fig.10.

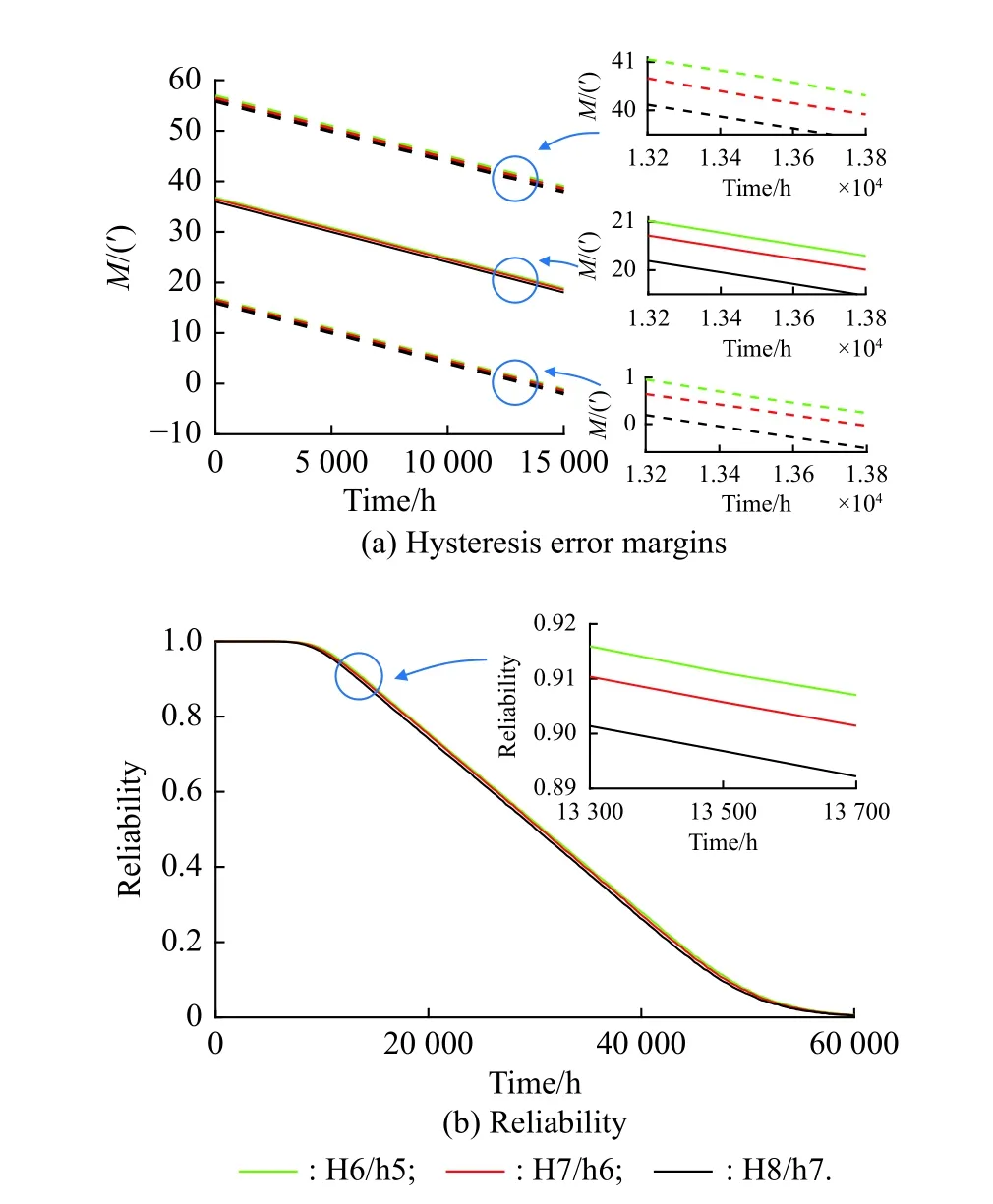
Fig.10 Hysteresis error margins and reliability under different clearance fits

From Fig.10, the bigger the clearance fit is, the smaller the hysteresis error margin and reliability are.However, the changes in the margin and reliability under different clearance fits are small.

(iv) Coefficient of linear thermal expansion

By substituting (10) and (11) into (9), the sum of the effects of thermal expansion in the gear pairsacandbcis

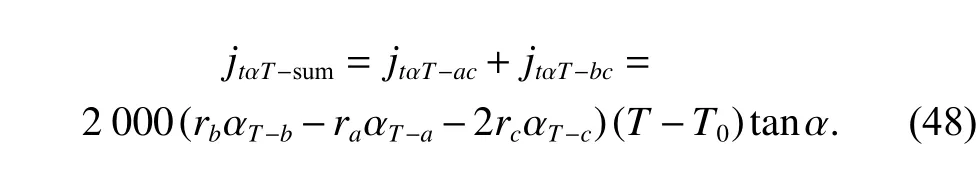
Since the materials of gears are the same, the linear expansion coefficients of gears follow the same distribution,i.e., αT～N(μαT,σαT).Then,jtαT?sumis also a random variable following the normal distribution with the mean value and variance,

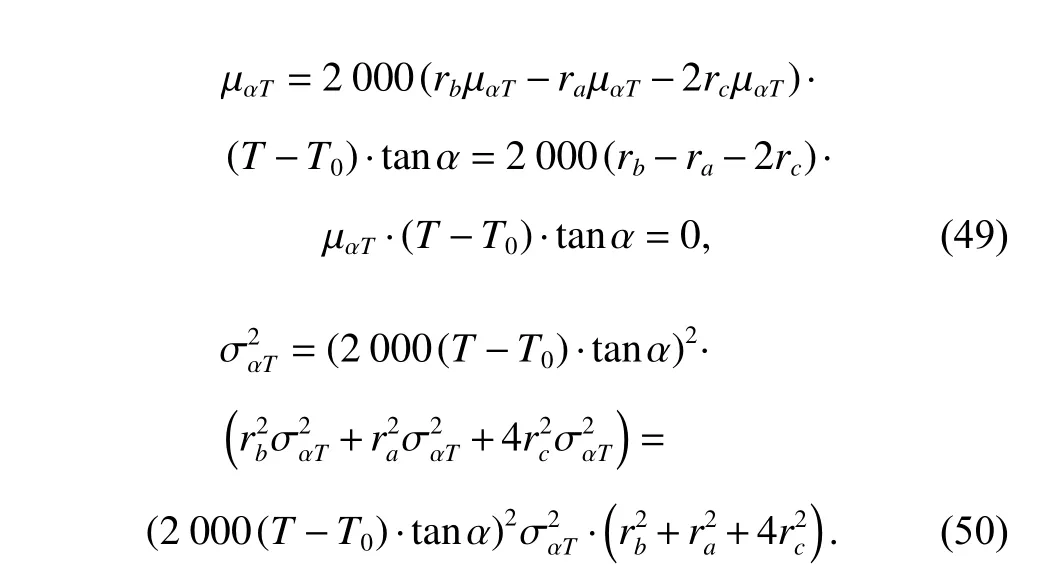
From (49), it can be seen that the mean values ofαT?iexert no influences on the circumferential backlashes caused by the thermal expansion of materials.Therefore,we only consider how the coefficient of variation ofαT?iaffects the hysteresis error margin and reliability.We vary the coefficient of variation from its original value to its 0.5 times and 1.5 times respectively while keeping other parameters unchanged, and calculate the hysteresis error margin and its reliability, shown in Fig.11.

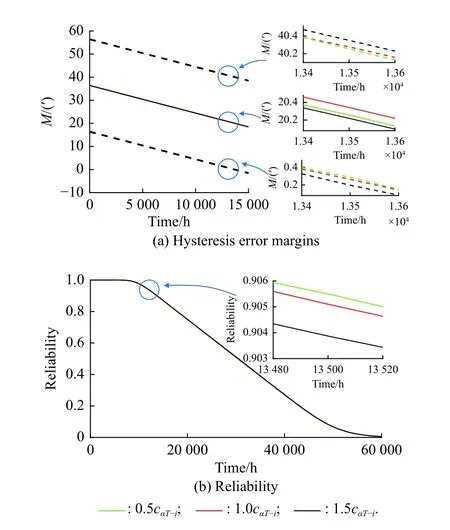
Fig.11 Hysteresis error margins and the reliability under different coefficients of αT?i

From Fig.11, the hysteresis error margin and reliability hardly change under different coefficients of variation ofαT?i.

(v) Comparison among manufacturing tolerances

In the reliability design process, the manufacturing errors that are sensitive to the performance margin and reliability usually gain more attention.Here we focus on the hysteresis error margin and reliability of the planetary reducer at 15 000 h, denoted asR(15 000), and explore how the variations of manufacturing tolerances influenceR(15 000).The corresponding hysteresis error margin and reliability results are shown in Fig.12.

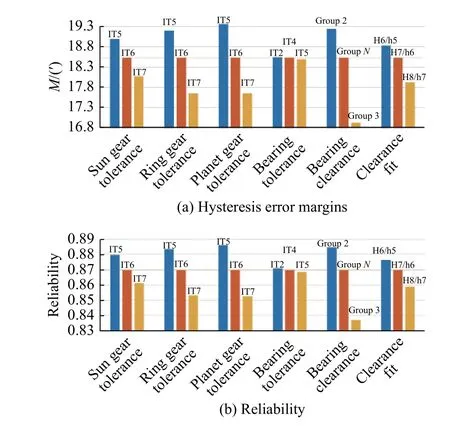
Fig.12 Hysteresis error margins and reliability under different manufacturing tolerances at 15 000 h

From Fig.12, the sensitivity of these manufacturing tolerances on the hysteresis error margin and reliability are consistent and can be sorted: bearing clearance >planet gear tolerance > ring gear tolerance > sun gear tolerance > clearance fit > bearing tolerance.Therefore, it is appropriate to reduce the manufacturing uncertainties to improve the reliability of the planetary reducer, such as choosing smaller tolerance of radial internal clearance of bearing and gear tolerances.

5.3.2 Reliability sensitivity analysis for operational and environmental conditions

As for the planetary reducer, the operational and environmental conditions considered are the environmental temperature and the wear rate according to Section 3.2.In this section, the reliability sensitivity analysis is implemented for the environmental temperature and the wear rate.

(i) Environmental temperature

For the environmental temperature, we vary its mean from its original value by 20 °C lower and 20 °C higher(i.e., 5 °C and 45 °C) and the coefficients of variance from its original value by 0.5 times and 1.5 times of it respectively while keeping other parameters unchanged.The hysteresis error margin and reliability under different means and coefficients of variance of environmental temperature are shown in Fig.13 and Fig.14.

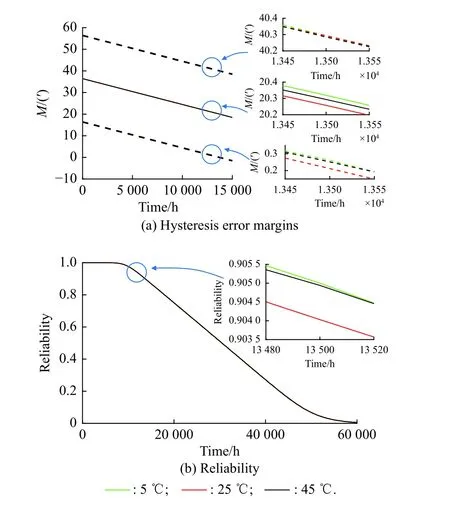
Fig.13 Hysteresis error margins and reliability under different means of the environmental temperature

From Fig.13 and Fig.14, the hysteresis error margin and reliability hardly change under different means and coefficients of variance of environmental temperature.

(ii) Wear rate

For the wear rate, we vary its mean from its original value to 80% and 120% of it and the coefficient of variance from its original value to 0.5 times and 1.5 times of it respectively while keeping other parameters unchanged.The hysteresis error margin and reliability under different means and coefficients of variance of the wear rate are shown in Fig.15 and Fig.16.

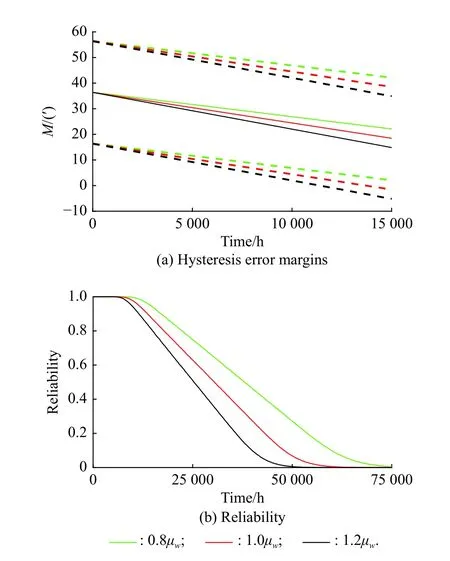
Fig.15 Hysteresis error margins and the reliability under different means of the wear rate

From Fig.15 and Fig.16, the following results can be obtained:

i) From Fig.15 (a), the larger the mean of the wear rate is, the bigger the absolute value of the slope of the margin curve is, which indicates that the performance margin degrades faster under a larger wear rate; corresponding to the result in Fig.15 (b), the reliability of the planetary reducer degrades faster.

ii) From Fig.16, there is a slight increase in the width of 90% confidence interval of the hysteresis error margin as the coefficient of variance increases, and the larger the coefficient of variance is, the earlier the reliability degrades.

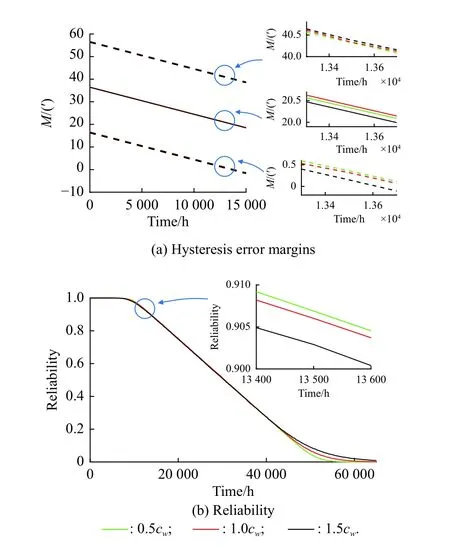
Fig.16 Hysteresis error margins and the reliability under different coefficients of variance of the wear rate

iii) Compared with the variance, the mean of the wear rate has a larger influence on the performance margin and reliability.

In summary, the mean of the wear rate exerts a larger influence on the hysteresis error margin and reliability of the planetary reducer than the coefficient of variance.Thus, decreasing the mean of the wear rate is an efficient method, such as improving lubrication conditions in the process of the operation, to decrease the degradation rate of the hysteresis error margin and increase the reliability of the planetary reducer.

5.3.3 Reliability sensitivity analysis for performance threshold

Different performance thresholds give different functional boundaries of the system.In order to explore the impact of different performance thresholds on the performance margins and reliability of harmonic reducers, we selected the two error grades of the planetary reducer, i.e.,GradeM, and GradeG(original grade) while keeping other parameters unchanged.The hysteresis error margin and reliability under different error grades of the performance threshold are shown in Fig.17.

From Fig.17, the performance threshold has a great impact on the hysteresis error margin and reliability, and the hysteresis error margin is smaller and the reliability degrades earlier as the hysteresis error threshold decreases.The uncertainties in the performance threshold usually come from the vague recognition of the function boundary of the system; hence, to evaluate the reliability precisely, a clear understanding of the performance thresholds is of vital importance.

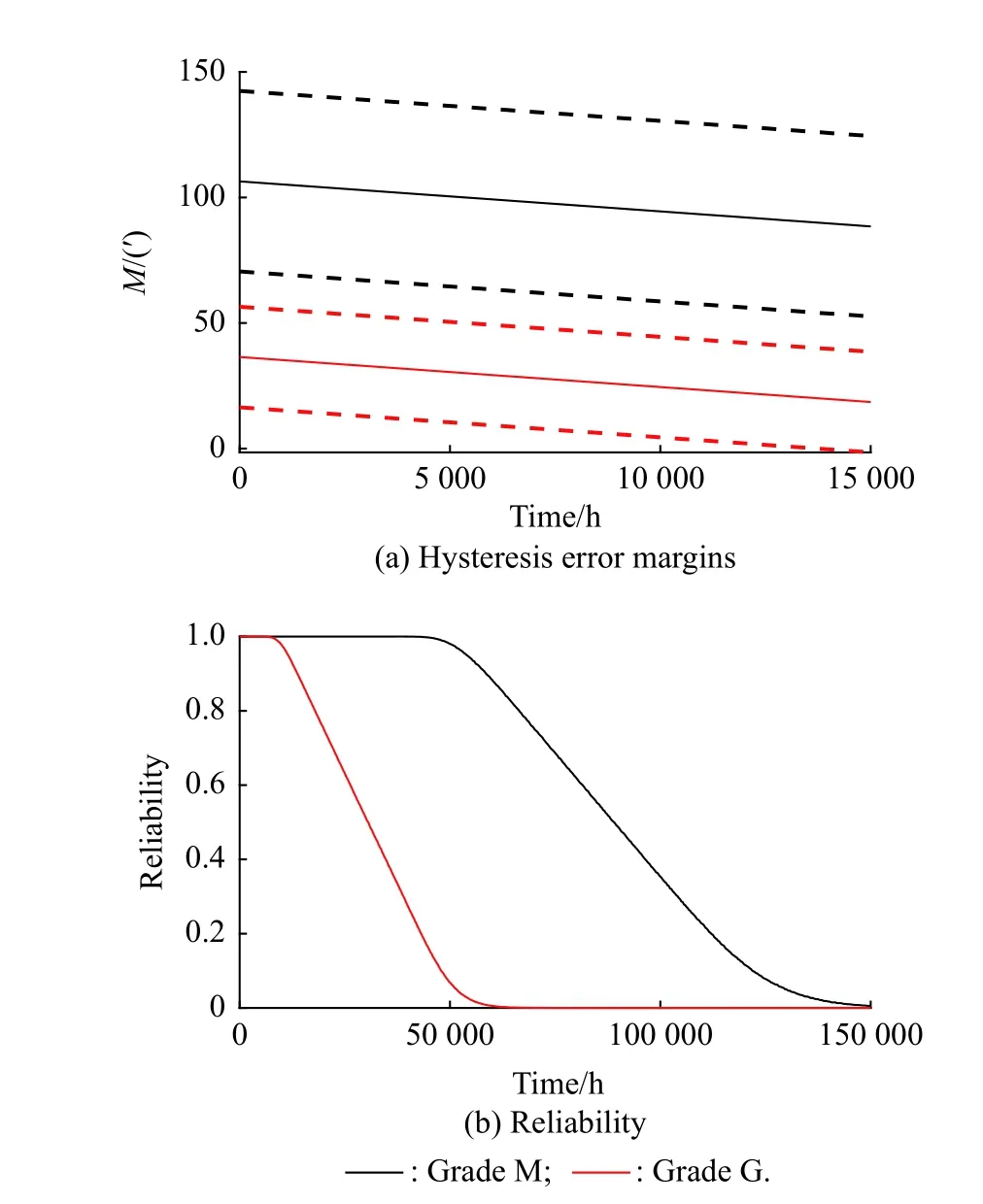
Fig.17 Hysteresis error margins and the reliability under different error grades of performance thresholds

6.Conclusions

The planetary reducer is a common type of transmission mechanism.In practical applications, the hysteresis error is one of the key performance parameters to describe its transmission performance.Aiming at the hysteresis error,this paper presents a performance margin modeling and belief reliability analysis of the planetary reducer considering the wear and multi-source uncertainties.Some conclusions can be drawn as follows:

(i) Based on the structural relationships of components and the influence of wear on the hysteresis error of the planetary reducer, the theoretical model considering degradation for the hysteresis error is constructed, and the corresponding margin degradation model is given by introducing the threshold.

(ii) Multi-source uncertainties are analyzed and quantified separately, including the manufacturing errors, the uncertainties in operational and environmental conditions, and the uncertainties in performance thresholds.In the quantification of these uncertainties, the manufacturing information of planetary reducers is utilized, such as the manufacturing tolerance grades for gears and bearings, the material of components and their physical properties, and the error grades of planetary reducers.The probability theory is employed to quantify these uncertainties.

(iii) Based on the performance margin, the belief reliability model is given by measuring the probability of the performance margin larger than 0, which fills up the gap between the performance modeling and the reliability modeling focused on the hysteresis error of planetary reducers.

(iv) A numerical study of the planetary reducer and the reliability sensitivity analysis is conducted, which shows the practicability of the proposed method.The results show that the proposed method can provide guidance to improve the reliability of planetary reducers by reducing manufacturing uncertainties during the manufacturing process and reducing the degradation rate during the usage process of planetary reducers, such as improving the grades of bearing clearance and gear tolerances and selecting appropriate lubrication methods.Additionally, the results show that precise recognition in the performance threshold plays an important part in evaluating the reliability of planetary reducers.

The planetary reducer has broad applications in practice, such as the mechanical transmissions of helicopters,automobiles, and aircraft engines.Therefore, the results of this paper can provide references for the reliability analysis and evaluation of these products.On the other hand, the method of this paper is not limited to the planetary reducer and can be extended to the reliability modeling and analysis of other kinds of gear-drive mechanisms.Beyond the work in this paper, there are still some issues that deserve further research.In this paper, we choose the hysteresis error as the key performance parameter of the transmission characteristics of the planetary reducer and conduct belief reliability analysis.In practice, there are many other parameters that can describe the transmission characteristics of the planetary reducer, such as the transmission error and the transmission efficiency.Future work can aim at the reliability modeling considering the coupling of these performance parameters.