CHEN Ying, MA Qichao, WANG Ze, and LI Yingyi

1.Science and Technology on Reliability and Environmental Engineering Laboratory, Beihang University, Beijing 100191, China;

2.Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621999, China

Abstract: In complex systems, functional dependency and physical dependency may have a coupling effect.In this paper,the reliability of a k-out-of-n system is analyzed considering loadsharing effect and failure mechanism (FM) propagation.Three types of FMs are considered and an accumulative damage model is proposed to illustrate the system behavior of the k-out-of-n system and the coupling effect between load-sharing effect and FM propagation effect.A combinational algorithm based on Binary decision diagram (BDD) and Monte-Carlo simulation is presented to evaluate the complex system behavior and reliability of the k-out-of-n system.A current stabilizing system that consists of a 3-out-of-6 subsystem with FM propagation effect is presented as a case to illustrate the complex behavior and to verify the applicability of the proposed method.Due to the coupling effect change, the main mechanism and failure mode will be changed, and the system lifetime is shortened.Reasons are analyzed and results show that different sensitivity factors of three different FMs lead to the change of the development rate, thus changing the failure scenario.Neglecting the coupling effect may lead to an incomplete and ineffective measuring and monitoring plan.Design strategies must be adopted to make the FM propagation insensitive to load-sharing effect.

Keywords: k-out-of-n system, load-sharing effect, failure mechanism propagation, damage factor model, combinational algorithm.

1.Introduction

In the field of engineering application, increasing attention has been drawn to a phenomenon known as failure dependence, for it always brings about the plunge of system reliability by incurring joint-failure [1].These dependencies include functional dependency (FDEP) and common cause failure (CCF).Among them, the former is caused by the functional structure, including load-sharing effect, and failure isolation effect.The latter is caused by physical changes, such as failure propagation effect,cascade failure effect, and so on.In addition, these dependencies often have many coupling relationships with each other.

load-sharing effect is a kind of functional dependence ink-out-of-nsystems where all components share the working load under some specific rules.When one component fails, load will be automatically transmitted to the remaining functional survivors [2].Extensive work about the reliability of thek-out-of-nsystem with load-sharing effect has been done, which mainly concentrates on loadsharing rules [3?5], load history and lifetime models[6?8], etc.To evaluate the reliability of load-sharing systems, load history, lifetime models including prognostics health management (PHM) [9], accelerated failure time model (AFTM) [10], tampered failure rate (TFR) [11]and the cumulative models have been developed.Recently the cumulative models have been widely applied because they can describe the change of system behavior caused by load variation.Liu et al.constructed reliability models for load-sharing systems with degrading components [12].The study showed that constant variable load has a cumulative impact on a system.Based on the Miner cumulative damage theory and the total probability formula, Hao et al.analyzed the reliability of load-sharing parallel systems and provided an insight into the load-redistribution process [13].Huang et al.introduced the concept of cumulative time to reflect the aging effect in each state with arbitrary failure distributions [14].The cumulative time in all states was combined in a unified manner to express the reliability function of a single component.In one of our previous work, the failure mechanism cumulative (FMC) model has been proposed to describe the complicated loading history ofk-out-of-nsystem with load-sharing effect.We provided the concept of the failure mechanism damage accumulation to explain the change of the failure rate at each loading stage by using arbitrary failure distributions [15].

The propagated failure, which is a kind of CCF, is the failure originating from a system component which causes extensive damage to other components [16].Failure propagation can be observed in all kinds of complex systems.For example, in network systems, failure of one node cascades to other nodes that results in severe collapse or widespread blackouts.In fault tolerant system,such ask-out-of-n, the behavior of propagated failure should be studied thoroughly to eliminate potential risks [17].

Ge et al.classified the component failure into the local failure and the propagated failure [17].The latter can be divided into two typical categories, the one with global effect and the other one with selective effect.Reliability of various systems suffering from the propagated failure with global or selective effect has been analyzed, such as multi-state systems [1,18], non-repairable phased-mission systems [19] and cold/hot standby systems [20], with the modeling methods including the universal generation method [21] and the binary decision diagram (BDD)method [22,23].Dependent propagated failure is defined as the failure that the degree of damage caused by a propagated failure depends upon the status of other components or the malfunction order of components [22].Zhao et al.studied the dependent competing effect of soft failure and hard failure in degrading system [23].The methods used for the modeling dependent failure process include Bayesian [24?26], Petri net [27], and BDD method [22].

In summary, many studies have concentrated on failure propagation effect and load-sharing effect individually.However, very few works focus on thek-out-of-nsystem with load-sharing and propagated failure.Maattouk et al.[28] analyzed the reliability of multi-states system with load-sharing and propagation failure dependence by using the Markov process and the universal generating function method.In this paper, the coupling effect of load-sharing effect and failure mechanism (FM)propagation is studied in thek-out-of-nsystem.A combinational method of failure tree (FT), failure mechanism tree (FMT), BDD and Monte-Carlo simulation is applied to describe the dependent behavior and evaluate the dynamic reliability.

The main contribution includes three items.First, the concept of FM propagation is clarified; its influence on system failure behavior is explained in detail.Second, a damage accumulative model is presented, and with the conditional probability theory, reliability of the non-repairable binary system under the consideration of coupling effect of FM propagation and load-sharing effect is theoretically derived.Third, an improved BDD model is proposed to describe the dynamic evaluation of FM with the coupling effect, and a combinational simulation method with BDD logic and Monte Carlo method is presented.

The remainder of this paper is organized as follows.Section 2 illustrates the damage accumulative model considering both load-sharing effect and FM propagation.Section 3 proposes a combinational simulation method to solve the model.The FMT model and the flow diagram of BDD logic based on the simulation method are given in this section.Section 4 is a case study of a current stabilization system.The dynamic reliability of the system with load-sharing and FM propagation effect is evaluated.Finally, the conclusions of this paper are summarized in Section 5.

2.Damage model for coupling effect

In conformity with the triggered external factor, FMs can be categorized into three types, O-type FMs (FMs affected only by an operating load, such as current or voltage), E-type FMs (FMs affected only by environmental stress, such as temperature or vibration), and Ctype FMs (FMs affected by both operating load and environmental stress) [29].Due to the load-sharing effect,when one component fails, the load will automatically transmit to the remaining survivors.Thus, the development rate, i.e., the damage per unit time of O-type and Ctype FMs will be increased.However, the load redistribution will not affect E-type ones.Since the development rate of O-type and C-type FM is similar, only the changes of O-type are shown in Fig.1.

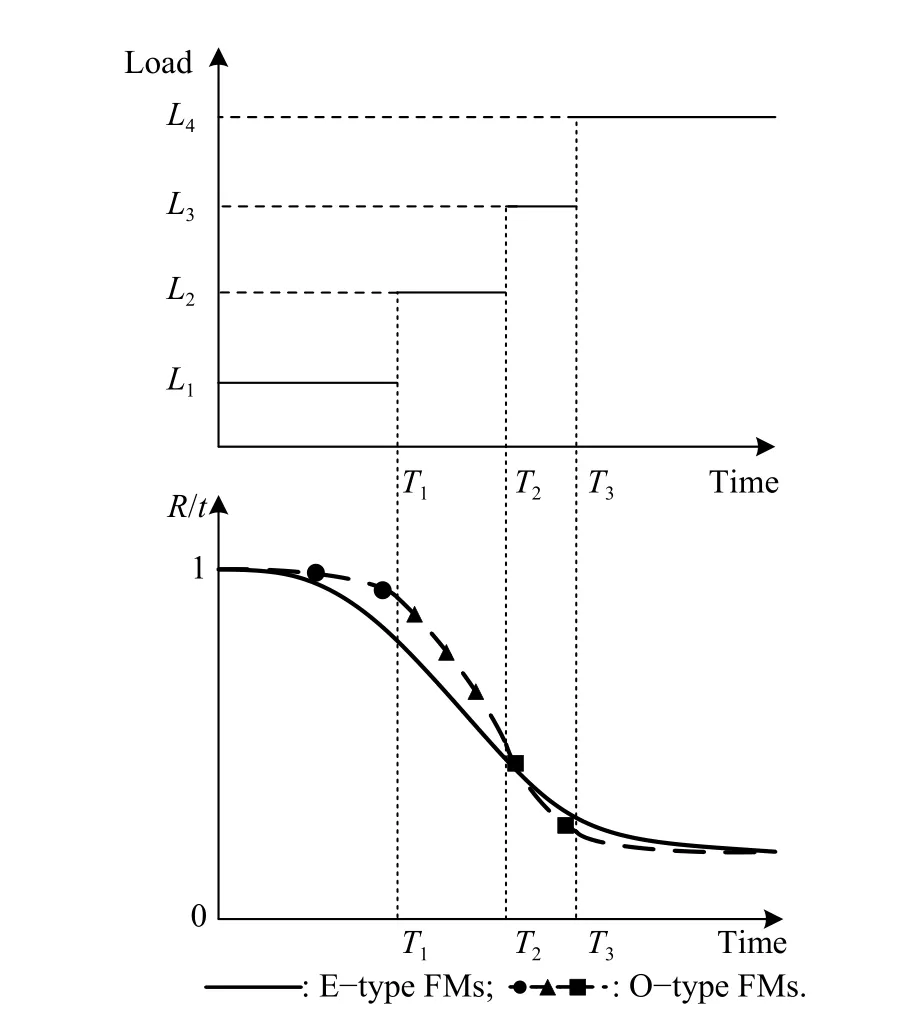
Fig.1 Different types of FMs in load-sharing system

Assume that there arenidentical components in ankout-of-nsystem, denoted asCi(i=1,2,···,n).Cihasmmechanisms,CMj(j=1,···,m).Due to the load-sharing effect, ak-out-of-nsystem experiencesn?k+1 load stages before system failure, denoted asS(p)(p=0,···,n?k).The time when the system enters into the next stage depends on the component whose failure time is the shortest.Assumeis the transition time matrix,is the stage transition time, which is the time when load-sharing effect happens.

When there is only load-sharing effect, assume that the development rate of FMs will keep constant at each stage for E-type FMs, because their development rate will not be affected by load-sharing effect, in different load stages,wherevErepresents the development rate of E-type FMs.For O-type FMs,.Although C-type will be affected by both load and environmental conditions, if the environmental conditions do not change, the development rate also has.The main FM of the components will be the first of the three FMs to reach the damage threshold, denoted asCM0.

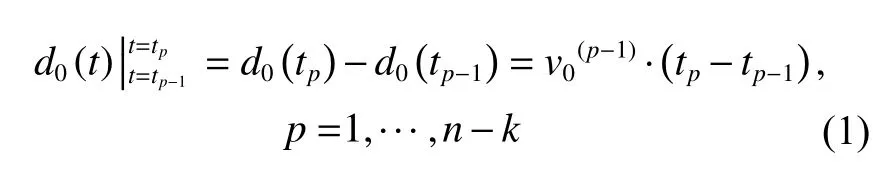
wherev0is the FM development rate ofCM0, andis the FM development rate ofCM0at the (p?1)th load stage.

Whent=tn?kthere aren?kcomponents being left in the system, the accumulative damage of the next failing component which will cause the failure of the system, i.e., is

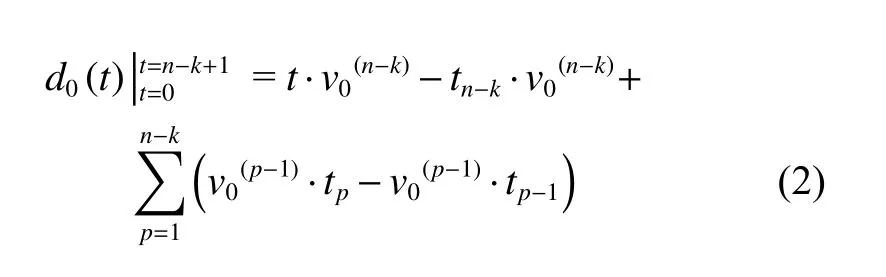
wherev0(n?k)is the FM development rate ofCM0at the(n?k)th load stage.

When one component of thek-out-of-nsystem fails due to its main FM,CM0affects the FM development rate of other components by affecting the surrounding environment, then, the development rate of E-type FM will change.C-type FMs will be affected by both the FM propagation and the load-sharing effect, their development rate will change more intensely.

Here, considering the load-sharing effect and FM propagation effect simultaneously, because the development rate of each type of FMs will be changed, the time when system goes into the next stage will also be changed except the first one, thus, the time matrix of load transition time will be

Based on (2), the accumulative damage caused byCM0is

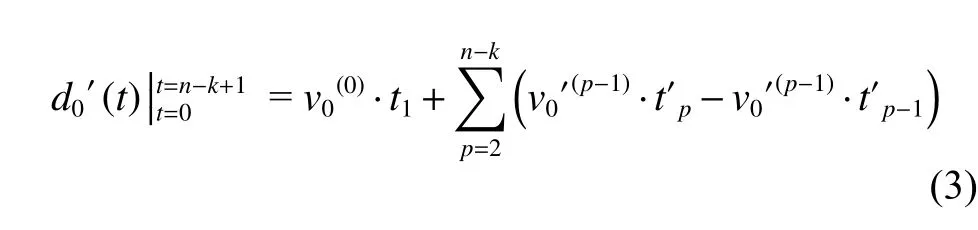
whered0(t) represents the damage of componentCidue to the independent influence ofCM0at timetwhen the load-sharing effect is the only effect to be considered,represents the damage when both the load-sharing effect and FM propagation effect are taken into account.

Aftert1, the damage of the remaining components because of the load-sharing effect, then at, the damage threshold will be reached again.Whent>t1, the probabigradually accumulates and the second load phase starts lity of component failure because of O-type FMs, assumed to be the eventA, is

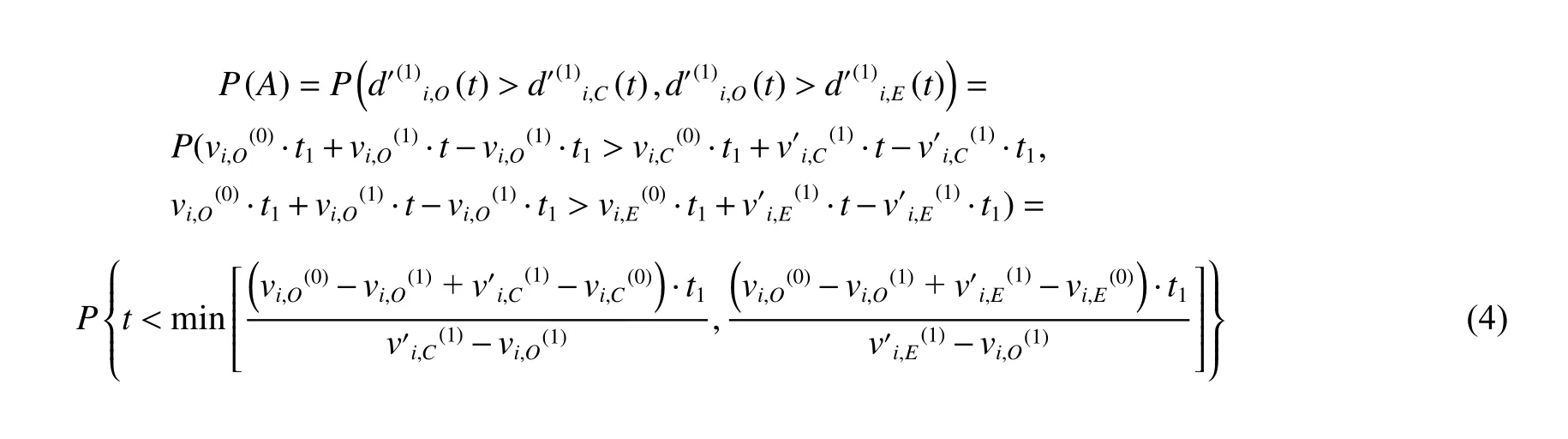
Similarly, the probability of component failure because of C-type FMs (Event B) and E-type FMs (Event D)are

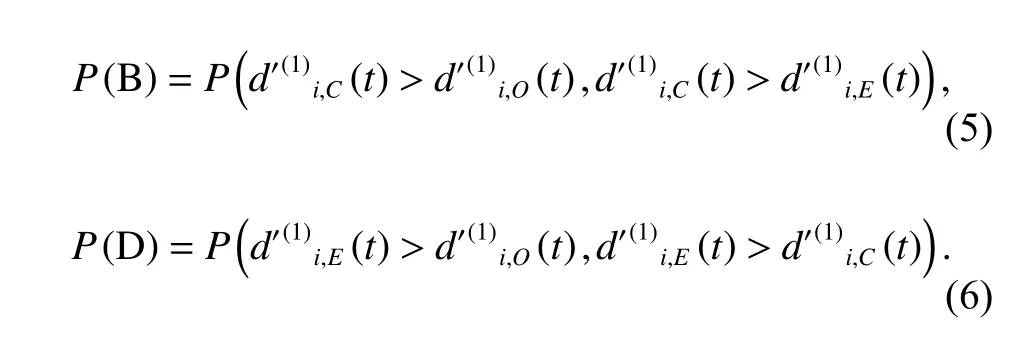
Then, the probability that component fails because of O-type FMs at any of time of the stageS(p)(Event F) is

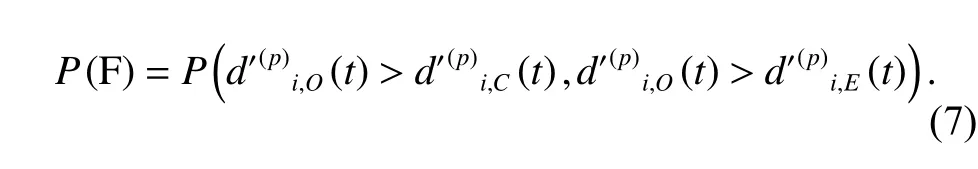
Based on (3), and considering at any timetinS(p),is

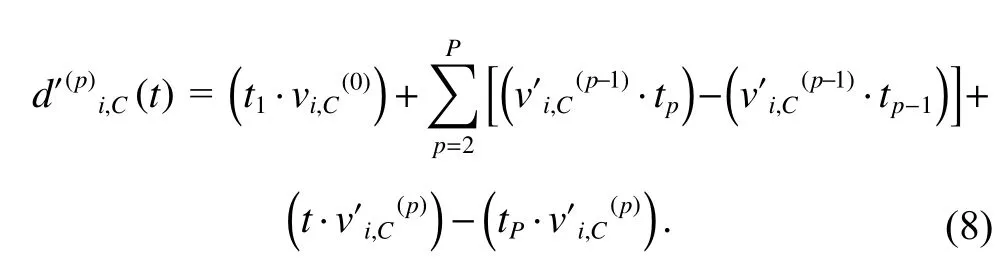
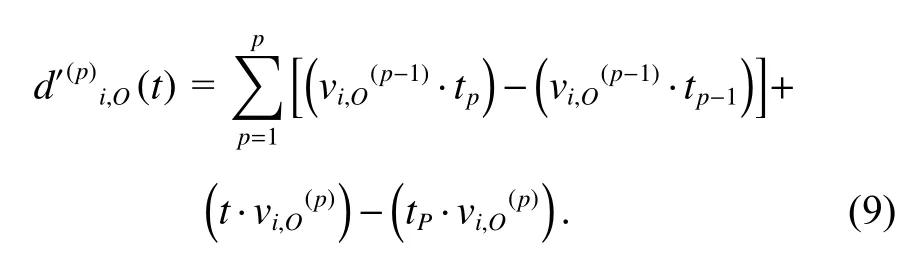
Herevi,Oremains unchanged because the O-type FMs are not affected by failure propagation.

It is worth noting that the load transition time applied in (8) and (9) is still, because the FM propagation effect only promotes the Ctype FMs and E-type FMs by changing the environmental load.Therefore, the necessary and insufficient condition for the occurrence of Event A and Event F is that only when the load-sharing effect exists in the system, the main FM of the component is an O-type FM.Under this condition, Events A and F mean that before and after the FM propagation occurs, neither the main FM nor its development rate has changed because of FM propagation,so the load transition time has not changed.

At any time of the stageS(p), component fails because of C-type FMs, assumed to be Event G, and component fails because of E-type FMs, assumed to be Event H,

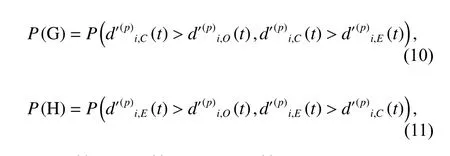
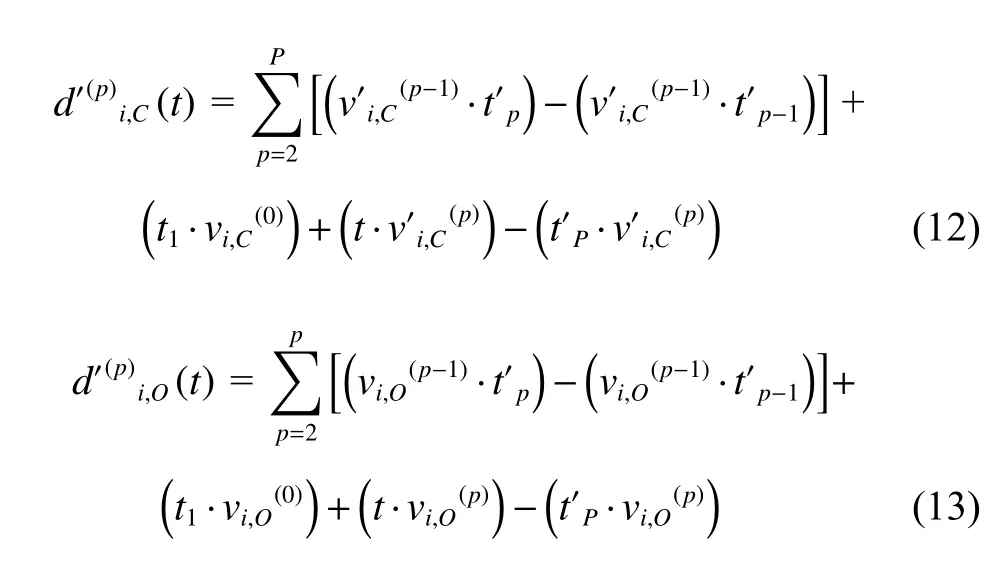
Based on the total probability theory, at any time of the load stageS(p) , the reliability of componentCi(i=1,2,···,n) is the sum of the probability of Events F, G and H, and the probability that the cumulative damage caused by the corresponding main mechanism is less than the threshold under the conditions of these events which is

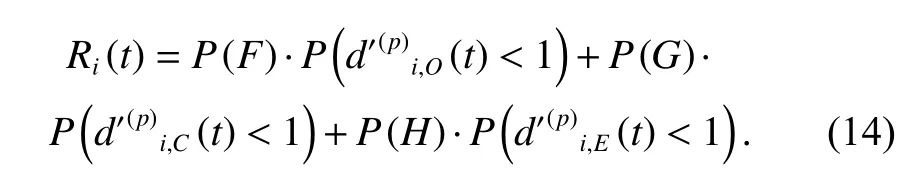
Based on the cumulative damages of (9) and (12), the probability that the corresponding damage is less than the threshold value can be obtained, as shown in (15) and(16), where the form ofis similar to (16).

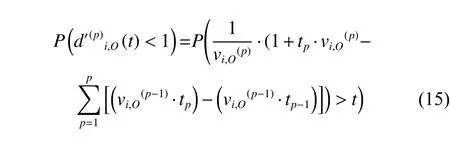
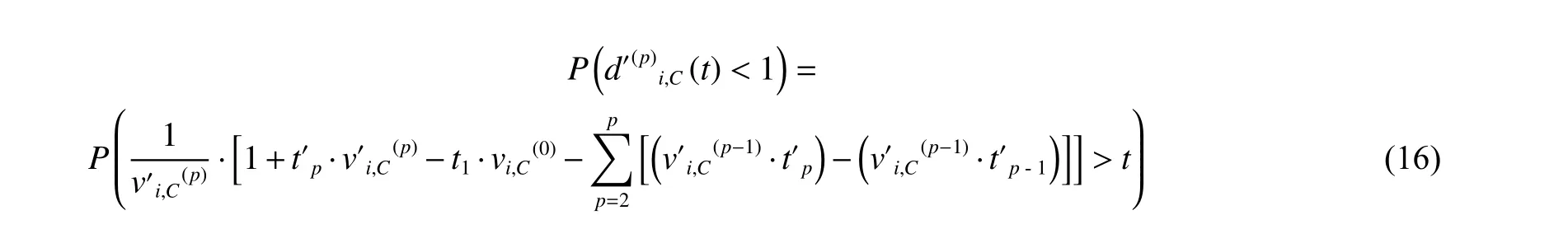
3.The proposed simulation method

In this paper, in order to describe the coupling effect between load-sharing and FM propagation, the FMT model is constructed, as shown in Fig.2.“MACC” and“MACO” represent FM acceleration and competition[30].Fiindicates the failure ofCi.TECrepresents the trigger event that a component ofk-out-of-nsystem fails.CM1?CMmare C-type-FMs and O-type-FMs exerting influence onCi(i=1,2,···,n) .represent the corresponding C-type-FMs and O-type-FMs with the renewed development rate because of the load-sharing effect after T ECoccurs.

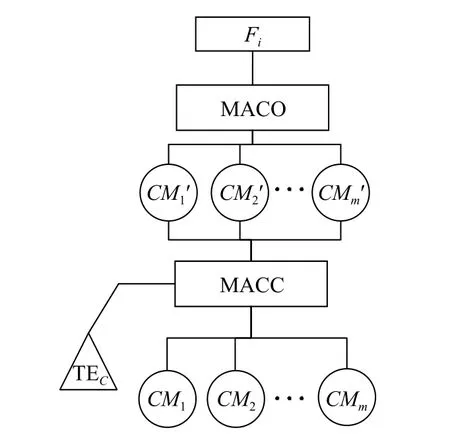
Fig.2 FMT model describing the load-sharing effect

The FMT model that describe the failure propagation effect is shown in Fig.3, whereCM2?CMmare O-type-FMs inCi(i=1,2,···,n) , andCM1is an E-type-FM.TEDrepresents the trigger event that FM propagation effect occurs when a component fails.representsCM1with the renewed rate because of the occurrence of TED.

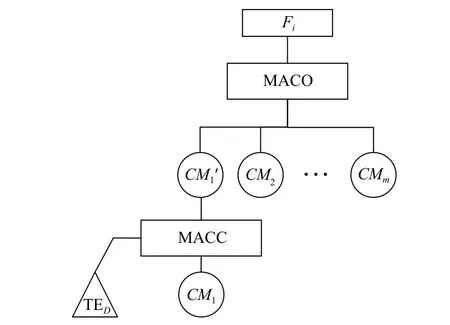
Fig.3 FMT model describing the failure propagation

The BDD method is used to solve the FMT model.However, in order to integrate load-sharing effect and FM propagation into the model, the traditional BDD method is improved, and the process is shown in Fig.4

Fig.4 Improved BDD model

In Fig.4, each circular non-root node represents a component.These non-root nodes have two extended edges,the “1” edge and the “0” edge, which respectively indicate the failure and reliability of the component.Each path from the top node to the root node “1” represents an event combination containing multiple components state.The sum of the probabilities of all these paths to the “1”node is the system failure probability; similarly, the sum of the probabilities of the component states in the path to the root node “0” is the reliability.A simple redundant system is taken as an example: componentsA,B, andCconstitute a subsystem and are connected in series withDto form the whole system.

Fig.4(a) is the BDD of the system when only the loadsharing effect is considered, where the corner mark indicates the times the component is affected by the load-sharing effect.When the FM propagation effect ofA,B, andConDis considered, more failure behaviors are introduced into the BDD.The dotted line represents the FM propagation effect caused by the failures ofA,B, andC, and the correspondingDis filled with gray to represent the influence of the FM propagation.The unmarked solid line derived from nodesA,B, andCindicates that it will point to the next node regardless of the state of the current node.

Based on the system functional structure, the system FT model can be obtained.To solve the system reliability model, a combinational method of BDD and Monte-Carlo simulation is proposed.The flow chart is illustrated in Fig.5.By using the probabilistic physics of failure (PPoF) method, the time to failure (TTF) distribution of each independent FM can be obtained as the input of the method.Then, simulating data are prepared with Monte Carlo sampling according to the distribution for each FM; simultaneously, time should be discretized.Reliability of each component on the independent influence of each FM at each discrete time point is calculated.Considering the influence of FM correlation and functional correlation among FMs, the reliability of each component under the action of multiple FMs at each discrete time point is obtained by means of simulation.Finally, the failure probability and reliability of each discrete time point can be obtained and the dynamic reliability of the system is calculated through the logic of BDD.

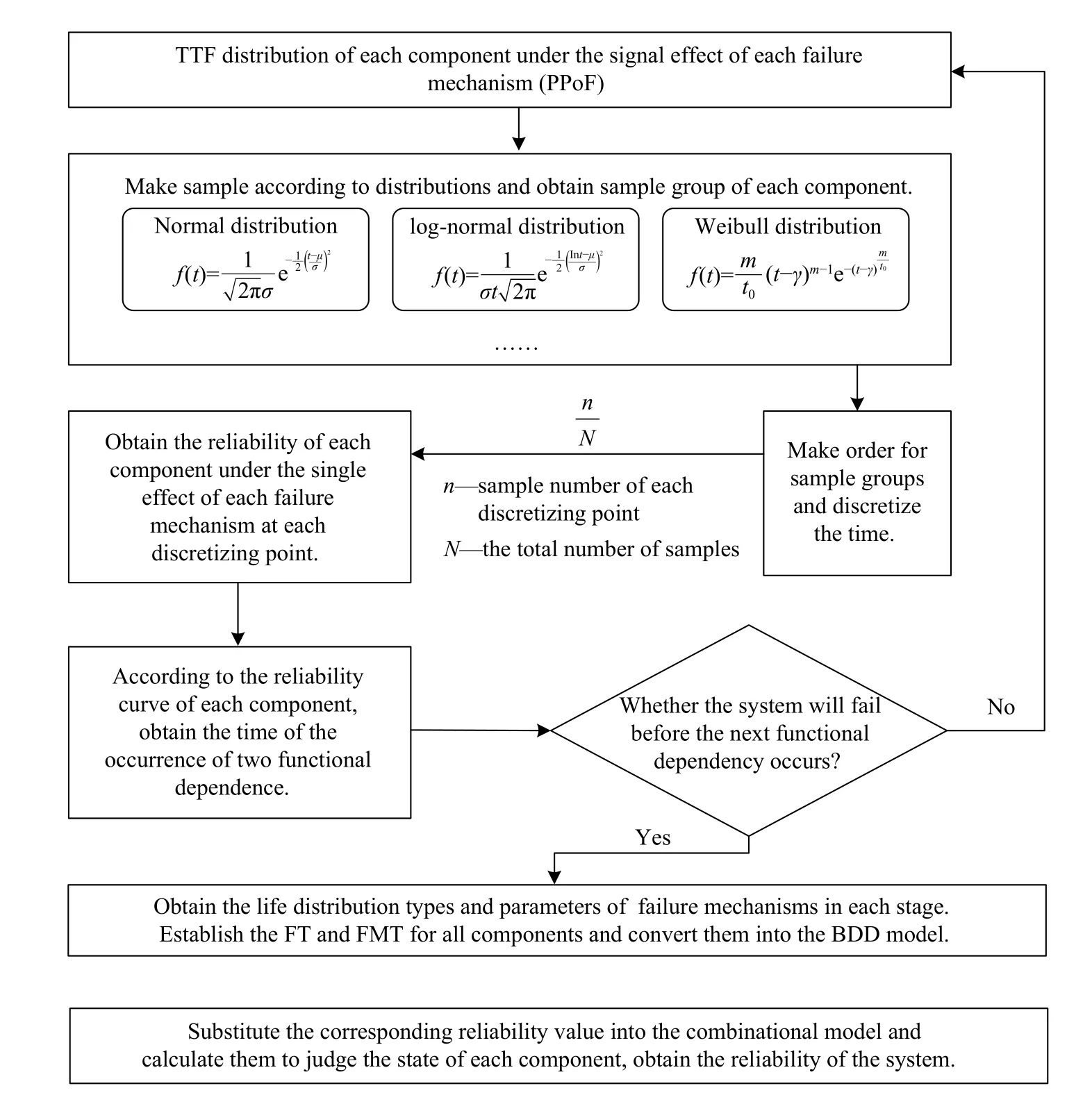
Fig.5 Flow chart of the proposed method

4.Case study

In the current stabilization system shown in Fig.6, the direct currentIiobtained by rectifying circuit and capacitor filter will pass through six parallel shunt resistors,R1?R6.In addition, there is a current stabilizerF1and a loadRLin a series structure, which is parallel to the system as a load.

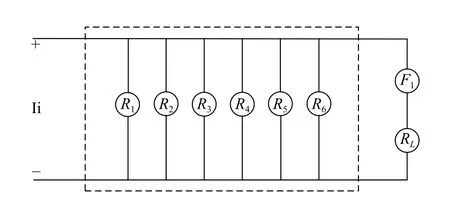
Fig.6 The current stabilization circuit

This is a typical 3-out-of-6 system, where the six protection metal film resistors are identical and have identical FMs, including electronic shock (ES), random vibration(RV) and silver migration (SM).There are two main FMs in the current stabilizer, solder joint creep (SJC) and material degradation (MD).And for the load resistorRL, the main FM is over current (OC).SM, MD, RV and SJC are degradative damage FMs, which means failure happens only when the damage accumulation exceeds the threshold.ES and OC are shock FMs.ES is a kind of compound random shock whose occurrence moment can be regarded as a random value under a certain distribution.Every time the shock occurs, the damage accumulates a little more until it exceeds the threshold and leads to the failure.However, OC is a sort of over-stress shock.The failure occurs suddenly only when the shock exceeds the threshold.There is no accumulating process of damage due to OC.

InRL, OC happens in two conditions.One is the large current passing throughF1due to the breakdown of any four protective resistors, the other is the failure ofF1itself.Therefore, when more than three protective resistors fail orF1fails, theRLwill have over-current failure.Based on the failure behavior of the system, the functional relationship among components and the relationship among FMs, the FT and FMT models of the system can be established using the modeling method proposed in Fig.3 and Fig.4.To simplify the analysis, the static FT and FMT models of the current stabilization system are transformed into the BDD model, which is shown in Fig.7.

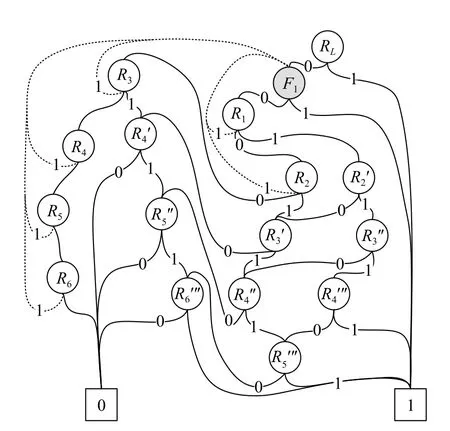
Fig.7 BDD model of the current stabilization circuit

Similar to Fig.4 and Fig.5, FMT and BDD models of the current stabilization system represent the FMs correlation and the failure relationship between components in the system respectively.After the failure of any one of the six resistors, each of the remaining five will suffer from more powerful current, which increases the development rate of FMs induced by electrical load, i.e., ES and SM in remain resistors.For the 3-out-of-6 system,prior to system failure, there are four load stages.During each load stage, the distribution parameters of the O-type FMs will change, takeR1andR2in the redundant system as examples, and the parameter changes are shown in Table 1.All data can be obtained through PPoF simulation.

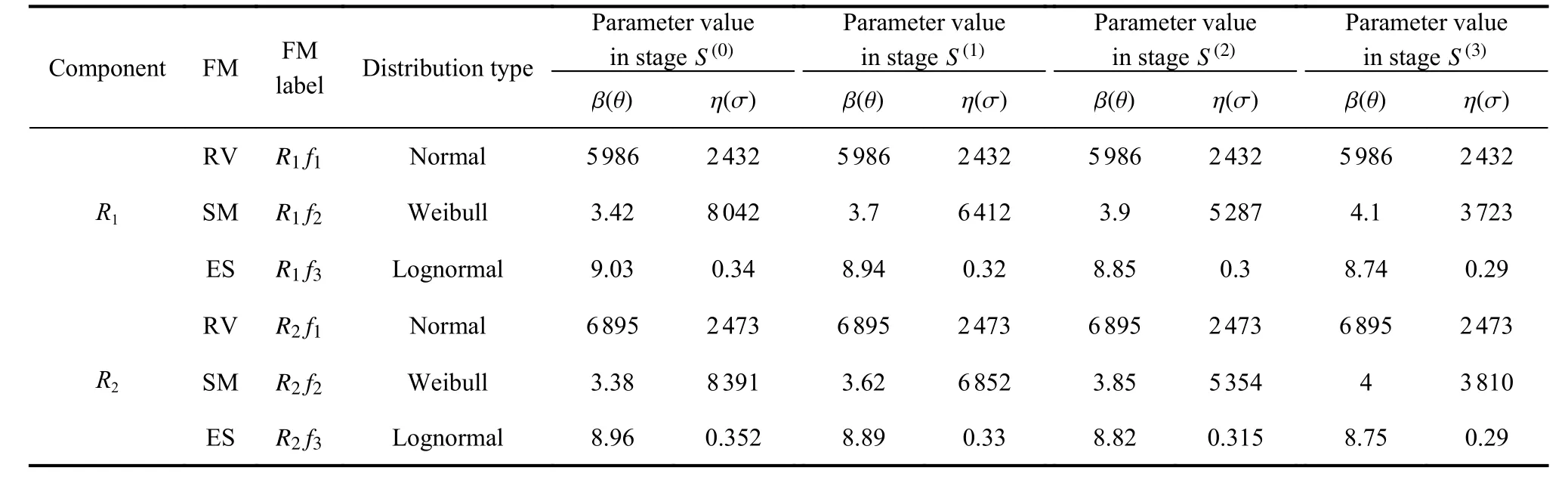
Table 1 Distribution of the FMs in the case study

In Table 1, the influence of load-sharing effect on ES and SM of resistors is taken into account.The increase of current has an effect on the development rate of these two FMs.

Via the PPoF method, the reliability ofR1suffering from RV, SM, and ES can be calculated respectively.The result is shown in Fig.8.R2?R6have similar reliability curves.ForF1, there are two FMs, MD and SJC, because of high temperature.The reliability curves of the current stabilizer on the influence of these two FMs are shown in Fig.9.

Assume that the failure criterion is that the reliability of the component or the system is smaller than 0.3.The moment that the reliability goes down to 0.3 for the first time is the lifetime.What can be observed from Fig.8 and Fig.9 is that, for resistorsR1?R6, the sequence of the development rate for the three FMs from small to large is RV, SM, ES, and forF1, the sequence is MD and SJC.Fig.10 is the reliability of resistorsR1?R6under the load-sharing effect.

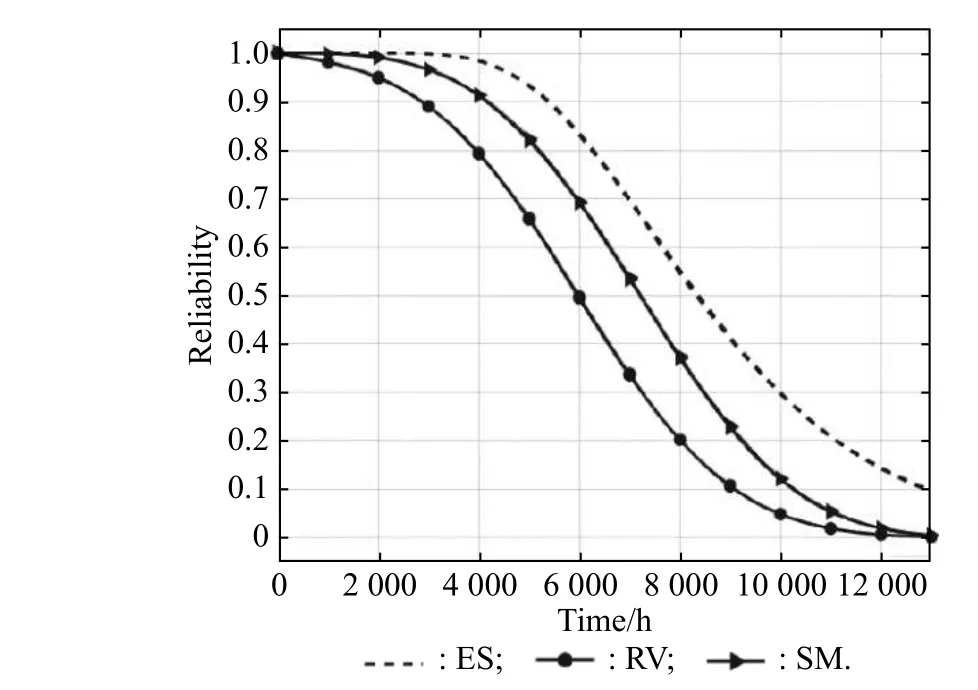
Fig.8 Reliability of R1 under different FMs

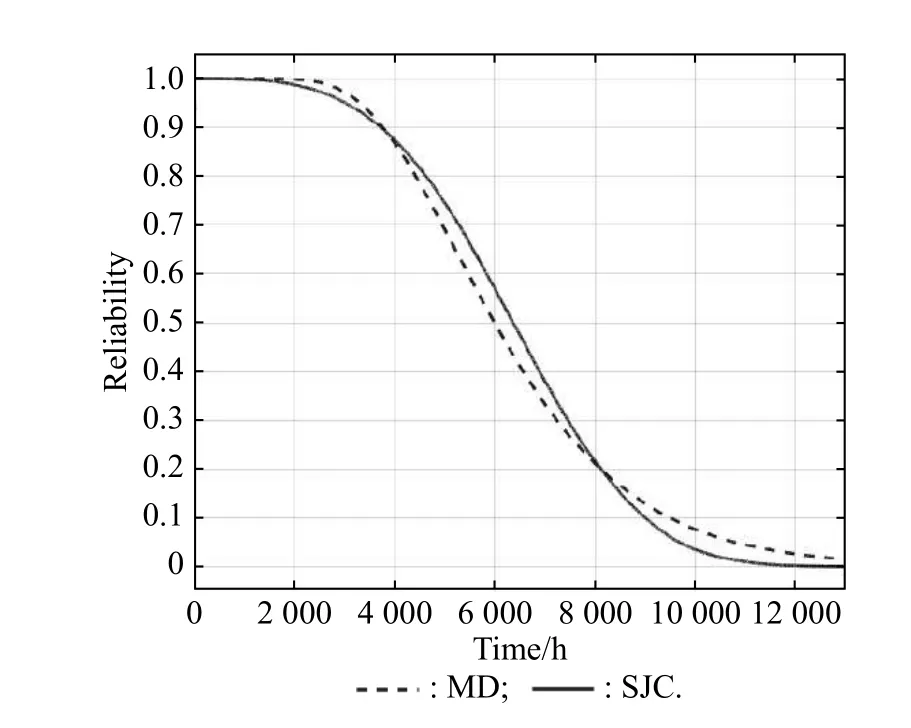
Fig.9 Reliability of current stabilizer under different FMs

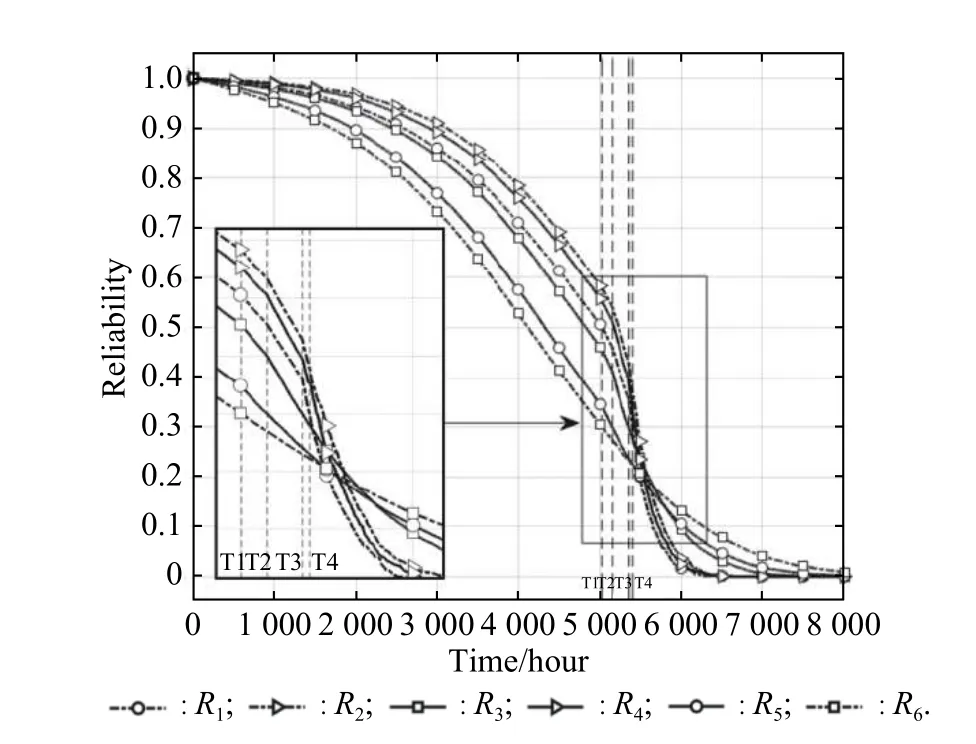
Fig.10 Reliability of resistors R1?R6 under the load-sharing effect

As shown in Fig.10, at time T1, which is 5022 h,R6reaches the failure threshold and fails.Then other resistors share the total current.Since the electrical load increases, the development rate of O-type FMs increases.At T2=5167 h,R5fails, and the load-sharing effect occurs again in the 3-out-of-6 system.The total current is shared by the remaining four resistors, and the development rate of the FMs of the remaining resistors increases furtherly.At T3=5356 h,R3fails.At T4= 5408 h,R1fails, and the 3-out-of-6 system fails at the same time.

As shown in Fig.11, the color solid line and the black dotted line are the reliability of the 3-out-of-6 system with and without load-sharing effect respectively.From the initial time (t=0) to point A, the 3-out-of-6 system operates normally.After the first load-sharing effect, the AB section of the curve, the reliability of the 3-out-of-6 system is significantly smaller than the one without considering load-sharing effect.The second load-sharing effect occurs at point B and the third load-sharing effect occurs at point C.Like the A-B section, the system reliability continues to decrease at a higher speed.

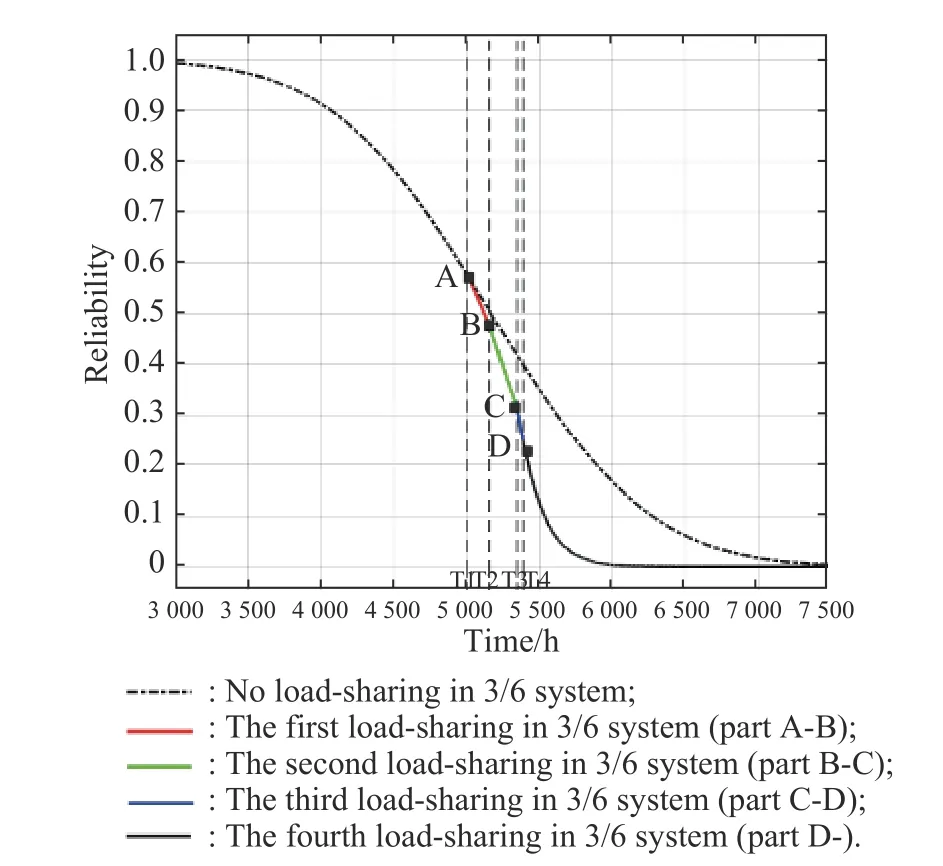
Fig.11 Reliability of 3-out-of-6 system under the load-sharing effect

Load-sharing effect not only affects the development rate of FM influencing the resistors, but also changes the main mechanism type.Before and after the first occurrence of load-sharing effect, the reliability curves ofR1on the influence of each FM are shown in Fig.12.

As can be seen in Fig.12, before and after the loadsharing effect, the influence on the reliability of E-type-FM (RV) does not change, while the curve of O-type-FMs (SM, ES) changes because of the increase of electrical stress load.When the failure threshold reached after 5236 h, SM is more likely to replace RV as the main FM ofR1.

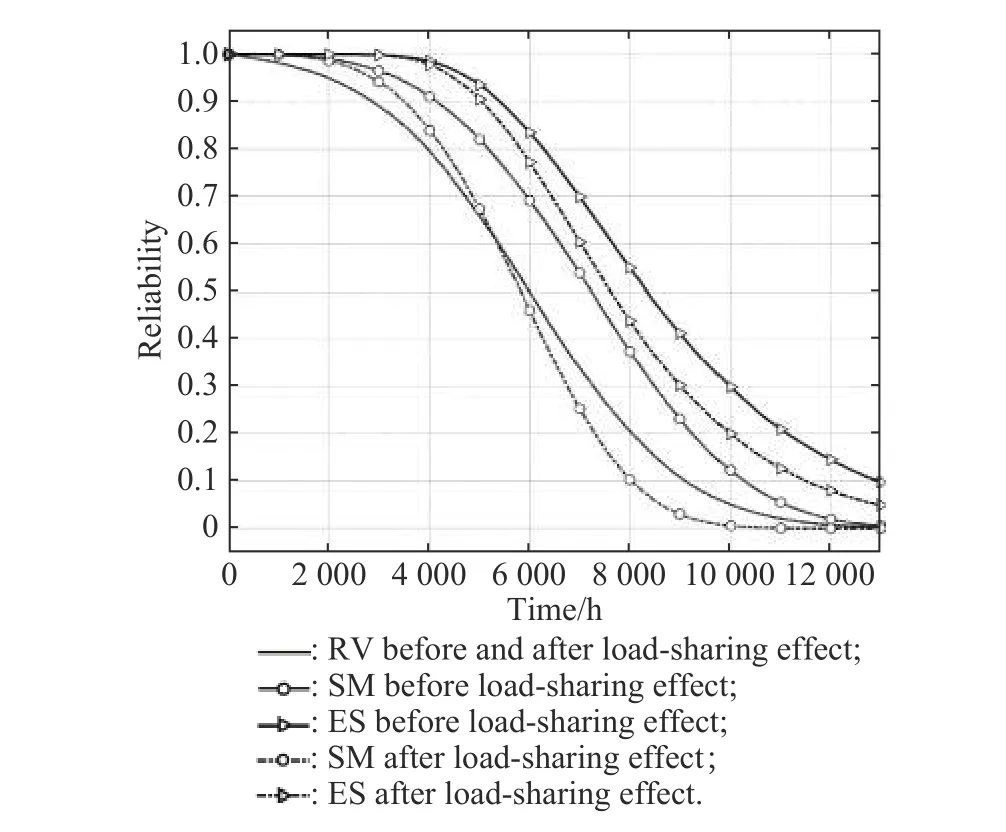
Fig.12 Reliability of R1 before and after the first occurrence of load-sharing effect

The SM in resistors will propagate and affect the creep inF1.When a resistor fails because of SM, the failure mode is functional open circuit.However, in fact, there is still a current going through the failed resistor, which causes a mass generation of heat.The failed resistor will not only result in current redistribution, but also change the local environment of other components.The development rate of creep inF1increases, resulting in the change of life distribution of SJC.The life distribution parameters ofF1and load resistor before and after FM propagation are shown in Table 2.The change of reliability of each component in this process is shown in Fig.13.

Table 2 Life distribution of branch system components under FM propagation

In Fig.13, it can be seen that the main mechanism of the five remain resistors changes after the first load-sharing effect.Therefore, when the second load-sharing effect occurs,R5fails because of SM rather than RV.In Fig.13, at the time before FM propagates, the reliability ofF1is greater than the reliability ofR3.However, after FM propagation effect occurs at T2, the failure development rate ofF1increases which leads to the result thatF1reaches its failure threshold earlier thanR3.In other words, the system fails because ofF1instead of the redundant subsystem.Thus, the system failure scenario changes, which is shown in Fig.14.

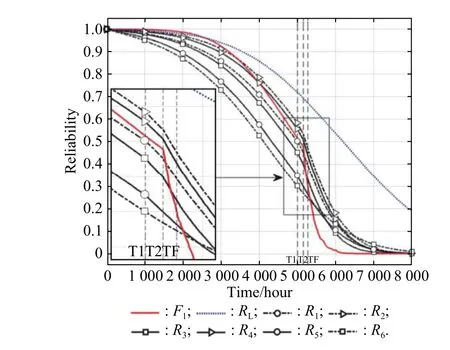
Fig.13 Reliability of each component after considering failure propagation and load-sharing

Fig.14 Change of the system failure scenario

The FM propagation caused by the failure ofR5shortens the lifetime of creep inF1.On the other hand,the load-sharing effect also increases the development rate of the O-type FMs of the rest resistors.The correlation of the two complex behaviors shortens the system life.Fig.15 shows the reliability of the system after considering FM propagation effect.

Based on Fig.15, the propagation effect of FM caused by load-sharing effect has a negative effect on the reliability of the system.At A, the first load-sharing effect occurs, which results in the main mechanism change of residual resistors.At B, the second load-sharing effect occurs, and the resistor that fails due to SM causes the FM propagation effect in the system by changing the local environment, which leads to the rapid increase of creep development rate inF1.At C and D, the third and fourth load-sharing effects occur, if propagation effect of FM is not considered, the system will fail at point D theoretically.However, it fails at E after considering the propagation effect, which is earlier than point D.

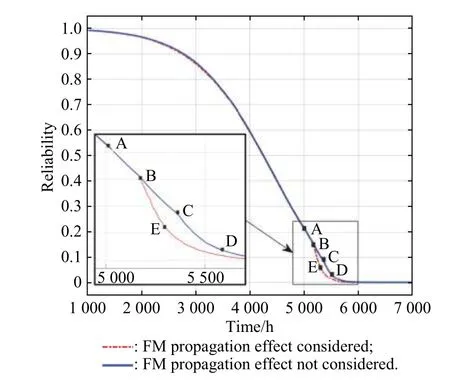
Fig.15 Reliability of the system with FM propagation

The simulation results show that the load-sharing effect in the 3-out-of-6 subsystem affects not only the reliability of the redundant subsystem, but also affects the FM of the component outside the subsystem through the FM propagation effect from the redundant components,which has a further negative impact on the system reliability.This coupling effect of load-sharing effect and FM propagation change the system failure scenario, thus the main mechanism and failure mode are also changed.The failure of the original system is caused by the failure of redundant parts successively, which exceeds the system redundancy threshold.However, when the FM propagation effect occurs, the system fails because of the current stabilizer before the failure of the redundant subsystem,which significantly reduces the time to failure of the system.

5.Conclusions

This paper proposes a damage model and a combinational simulation method to consider the correlation of the load-sharing effect and FM propagation ink-out-of-nsystems.Three types of FMs, C-type-FMs, E-type-FMs, and O-type-FMs, are considered.The O-type and C-type FMs are sensitive to load-sharing effect.E-type and C-type FMs are sensitive to the FM propagation effect.When different types of FMs exist in the components, the development rates will be accelerated by the coupling of the two failure dependencies, which have not been covered in previous studies.

The effective method using the FMT and BDD logic based on the simulation method has been developed for the calculation of the reliability of the complex behavior of the system considering load-sharing effect and FM propagation effect.This method requires the distribution of failure time of each failure mechanism predicted by the physics of failure (PoF) method, as well as the reliability calculated by the damage model.It has been demonstrated that using the data obtained from PPoF to evaluate the system reliability is superior to the conventional statistical-based method, because the failure data are extremely sparse for complex system.

Results of the case study show that the coupling effect may change system main failure mechanism and failure mode.Neglecting the coupling effect may lead to the incomplete and ineffective measuring and monitoring plan.For this case, design strategies must be adopted to make the FM propagation insensitive to load-sharing effect.And it is necessary to collect relevant failure data in engineering to further verify and study the phenomenon.