A method to realize NAVSOP by utilizing GNSS authorized signals
YUAN Ying, YU Feng,*, CHEN Yang, and ZHANG Niancheng
1.Key Laboratory of Space Photoelectric Detection and Perception, Nanjing 210016, China;
2.College of Aeronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Abstract: Navigation via signals of opportunity (NAVSOP) is able to realize positioning by making use of hundreds of different signals that are all around us.A method to realize NAVSOP for low earth orbit (LEO) satellites is proposed in this paper, in which the global navigation satellite system (GNSS) authorized signals are utilized as the signal of opportunity (SOP).At first, the carrier recovery technique is studied under the premise that the pseudo-code is unknown.Secondly, a method based on characteristics of Doppler frequency shift is proposed to recognize the navigation satellites.Thirdly, the extended Kalman filter (EKF) is utilized to estimate the orbital parameters by using carrier phase measurements.Finally, the proposed method is evaluated by using signals generated by a satellite navigation data simulator.The simulation results show that the proposed method can successfully realize navigation via GNSS authorized signals.
Keywords: navigation via signals of opportunity (NAVSOP),codeless technique, carrier recovery, satellite recognition, orbit determination.
1.Introduction
Known as navigation via signals of opportunity(NAVSOP), BAE systems’ new system is able to achieve users’ positioning by receiving and processing the signals already existing in the environment, such as Wi-Fi,TV, global navigation satellite system (GNSS) signals,and mobile phone signals [1,2].The proposal of NAVSOP provides new ideas for the efficient use of signals of opportunity (SOPs).Compared to the commonly used satellite navigation methods, NAVSOP’s advantages are obvious: the SOPs in the environment are sufficient and diverse; some SOPs possess high signal to noise ratio(SNR) and strong penetrability; and there is no need to develop new transmitters and receivers [2].Thus NAVSOP has attracted significant attention.In recent years, some researchers have realized NAVSOP based on broadcast signals, Wi-Fi signals, ultra-wideband (UWB)signals, etc [3?9].However, some considerable drawbacks make the development of NAVSOP a great challenge.In order to receive available SOP, the receiver must possess large bandwidth, high dynamic range and high sampling rate, the signal processing algorithm should be able to work when signals overlap with each other and the SNR is quite low [2].
Using navigation satellites to realize positioning is a very mature technology in modern life for low earth orbit(LEO) satellites [10].With the development of navigation systems, new navigation signals can improve the capability of availability and accuracy.However, for civilian users, the use of navigation signals may be restricted.For example, GPS III satellites possess the ability to quickly shut down the broadcast of civilian code in specific areas as needed, and the access of authorized signals are denied to civilian users [11].In this situation, traditional navigation technologies are no longer applicable,civil satellites are unable to provide navigation service normally, and the users may suffer huge economic losses.
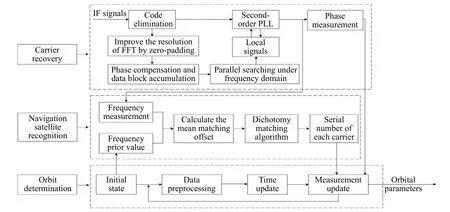
A method using GNSS authorized signals to realize NAVSOP is proposed, which can improve the reliability of navigation for civil satellites in orbit.There are several advantages to the usage of authorized signals compared to other radio signals.These advantages include:atomic clocks on the navigation satellites are the most accurate frequency standards, and the frequencies of authorized signals are very stable.The design of the constellation makes it possible that there are always enough visible satellites from any point in LEO at any time, ensuring considerable redundancy over the minimum requirement for positioning.Three key technologies are studied in this paper.The first one is the carrier recovery of GNSS authorized signals, the second one is the recognition of navigation satellites, and the third one is the orbit determination using phase measurements.
The authorized signals are utilized as the SOPs, the access of it is denied to civilian users because the pseudocode is encrypted.Without the knowledge of the pseudocode, a codeless technique has to be utilized for the reconstruction of the signal carrier.The codeless techniques were originally developed to against the antispoofing (AS) policy, and they have been widely utilized in geodetic surveying and crustal movement monitoring[12,13].There are four techniques that have been published in the past: squaring, cross-correlation, P-code aided L2 squaring and Z-tracking [13].However, except the squaring method, all the other three methods either require the assistance of pseudo-code, or L1 and L2 signals work together, which are not applicable in our scenario.Because of the lack of knowledge of the pseudo code, the squaring method performs significantly worse than an ideal phase lock loop.After squaring, the SNR is degraded by about 30 dB in general conditions [13], which means that the authorized signals are extremely difficult to be captured after squaring.Therefore, some strategies must be considered to increase the signal strength.Two strategies are applied.First, antenna gain is applied to enhance the signal strength.By employing the controlled radiation pattern antenna (CRPA), GNSS receivers can increase the signal power by 30 dB [14,15].In this situation, the signal is much easier to be captured and the accuracy of acquisition is greatly increased.Second, the signal acquisition algorithm proposed is able to enhance the signal strength by utilizing phase compensation and data block accumulation.The probability of detection and the probability of false alarm are introduced to analyze the performance of the acquisition algorithm.
Squaring processing results in an unmodulated, continuous carrier, whose phase can be measured.However,now that the pseudo-code and data code are eliminated,the carriers reconstructed are distinguished from each other only by their frequencies.In order to correctly recognize the navigation satellites in this situation, a new method based on the characteristics of the Doppler frequency is proposed [16].A dichotomy method is utilized to improve the efficiency.The errors of recognition for each satellite are calculated, a threshold is set to make sure the results are reliable.
The carrier phase measurements are obtained in the process of carrier recovery, and they are utilized as the observations for the extended Kalman filter (EKF) to update state variables.There are some successful precedents using Doppler frequency shift information to realize navigation.Autonomous orbit determination was realized by using the tracking and data relay satellite system(TDRSS) [17?19].Relay satellites transmit signals modulated by pseudo-code, the user satellites receive the signals and demodulate the signal with the same pseudocode to reconstruct the carrier.The orbital parameters are estimated based on Doppler frequency shift measurements.Another example is the Doppler orbit-ography and radio-positioning integrated by satellite (DORIS) [20?22].It has realized decimeter level real-time orbit determination.Ground-based radio beacons keep transmitting signals into the space, when satellites fly over, the satellites receive signals, measure the Doppler frequency shift and estimate the orbital parameters.These two systems confirm the feasibility of Doppler orbit determination,both of them work in a cooperative way.
This paper has developed a new technology to realize orbit determination for LEO satellites, which can be regarded as a special NAVSOP.Unlike TDRSS and DORIS, the proposed methods are expected to work in a noncooperative way.The effectiveness of the proposed methods is validated by semi-physical simulation experiments.The research provides an alternative navigation method, which improves the reliability of civil LEO satellites in orbit.
2.Carrier recovery
2.1 Analysis of signal strength
This paper takes the GPS L1 signal for example.In general, the signal power of authorized signals receivedPsis about ?133 dBm.The total noise power is given as
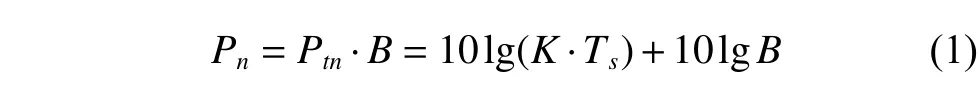
whereBis the system receiving bandwidth, for authorized code it is 20.46MHz .Ptnis the thermal noise,K=1.3806505×10?23J/K is the Boltzmann constant,andTsis the system temperature.In normal environment,Ts=20?C(293.5K) .The SNR and carrier-to-noise ratio(CNR) of the authorized code are calculated as
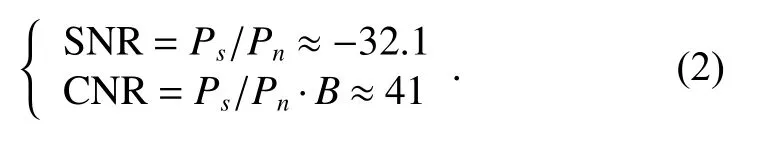
The pseudo-code is eliminated by the squaring method before signal acquisition.The squaring process must be performed in a bandwidth broad enough to include most of the spread-spectrum energy of the incoming signal.Because this bandwidth also includes significant noise,the squaring loss is huge.The squaring loss for a general squaring loop can be approximated [13] by
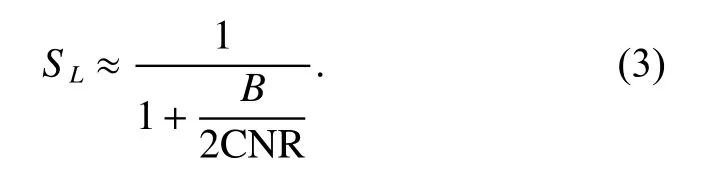
The squaring loss and root mean square (RMS) phase error under different C NRs are shown in Fig.1.
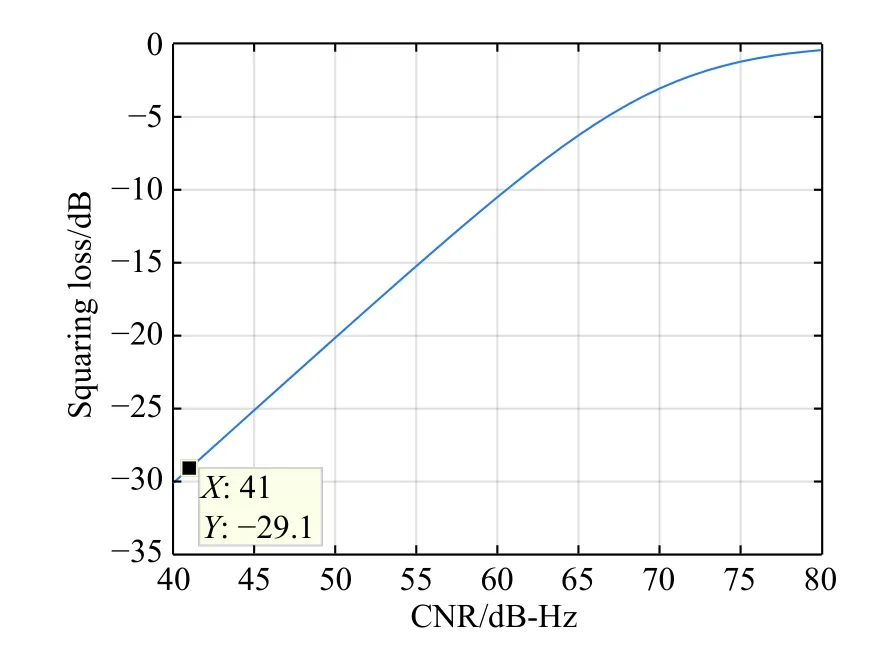
Fig.1 Squaring loss under different CNRs
The squaring loss when CNR=41dB-Hz is about?29.1 dB, the signal strength of the authorized signal is too weak to be captured after squaring.With the help of antenna gain, the signal strength can be increased to a certain extent.As Fig.1 shows, by increasing signal strength, the squaring loss is significantly decreased.The signal is much easier to be captured, which is quite beneficial to the implementation of the experiments.The higher the signal strength is, the better the result will be.With the development of related technologies, the signal strength can be further enhanced.However, this presents higher requirements for the antenna, leads to a bigger receiver and causes some extra cost [15].
2.2 Signal acquisition
Signal acquisition is the key step to measure the Doppler frequency shift and recover the carrier.For LEO satellites, the maximum Doppler frequency shift can be tens of thousands Hertz, which means that it will take a lot of time by using the serial search method.And although the antenna gain greatly increases the signal strength, the noise power is still much stronger than the signal power.If a fast Fourier transform (FFT) is performed for the squared signals directly, the target frequency is hard to detect.
Therefore, a signal acquisition algorithm is designed to work in a parallel way, and furthermore, it is able to enhance the signal strength before searching by utilizing phase compensation and data block accumulation.The whole process of signal acquisition is shown in Fig.2.
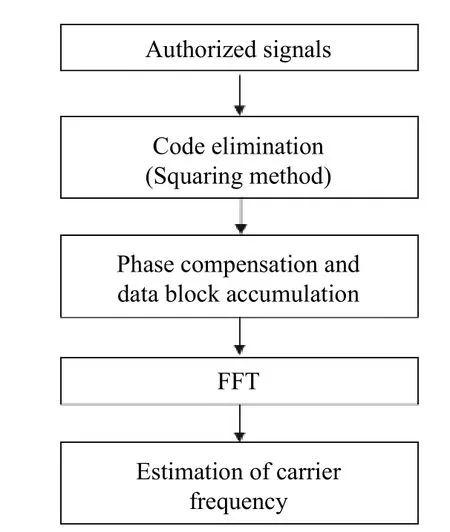
Fig.2 Whole process of signal acquisition
The mathematical model of GNSS authorized signals can be expressed as
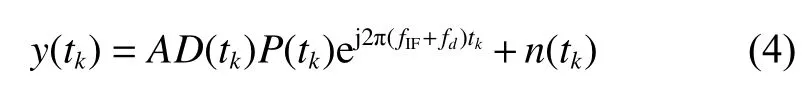
whereArepresents the signal amplitude,Pis the pseudo random noise (PRN),Dis the data code,fIFis the intermediate frequency,fdis the Doppler frequency shift,nis the noise, andtkis the time.
The squaring method is utilized to eliminate the pseudocode as
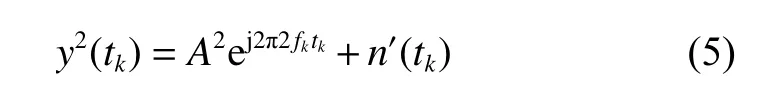
wherefk=fIF+fd.A signalp(tk) is generated locally to adjust the frequency of squared signals.The mathematical expression ofp(tk) is given as
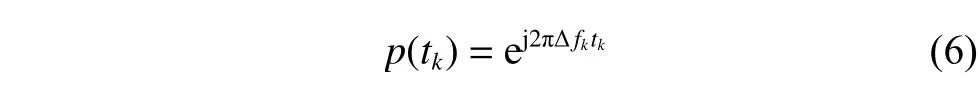
where Δfkis the frequency ofp(tk).The squared signals are multiplied byp(tk) as
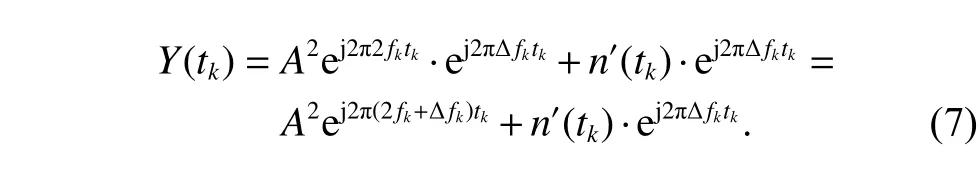
The signalY(tk) is divided intoLblocks, and the length of each block isTs.Ignore the noise and accumulate all the blocks, the result is derived as
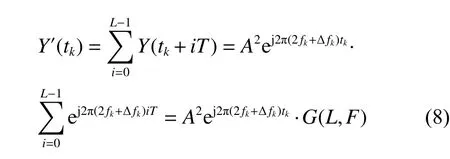
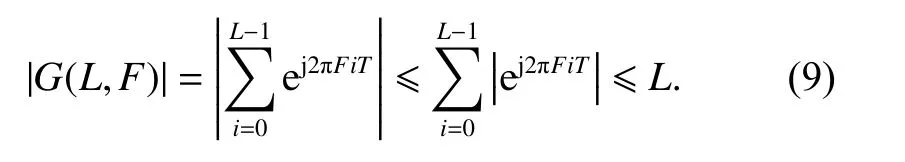
WhenF·T=Mis an integer, obviously ej2πFiT=1 and the signal strength can be increased toLtimes.Then the FFT is performed for the signalY′(tk).The peak amplitude of FFT results can be easily detected after squaring.The Doppler frequency shift can be easily calculated as
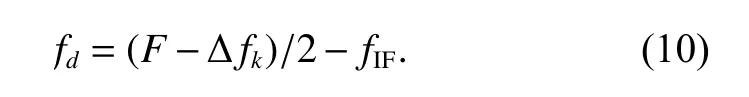
After accumulating, the signal power is improved by the square of the number of accumulationL, while the noise power is improved exponentially.Thus, the acquisition algorithm can improve the CNR of the squared signals.The increment is 10lgL.The relationship betweenLand the increment of C NR is shown in Fig.3.
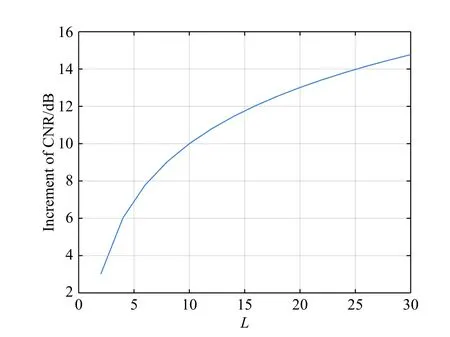
Fig.3 Relationship between L and the increment of CNR
As Fig.3 shows, the bigger the accumulation timesLis, the bigger the increment of CNR will be.However,whenLgrows, the slope is getting smaller, and the length of data block is reduced, which may cause signal distortion.A properLshould be selected to get an optimal performance.
2.3 Performance analysis of acquisition algorithm
The probability of detectionPDand the probability of false alarmPFAare introduced to analyze the performance of the acquisition algorithm.In theory,PDandPFAcan be calculated by the probability density function(PDF) of the decision variable under different conditions.However, the acquisition algorithm proposed is relatively complicated, the analytic expressions ofPDandPFAare hard to obtain.Thus multiple simulation experiments are carried out to obtainPDandPFAunder different CNRs.
The parameters of simulation experiments are set as follows.The length of data involved in signal acquisition is 80 ms, the length of the data block is set as 4 ms.The number of accumulationLis set as 20.The range of the CNR of the input signals is [40,80]Hz, the step size of it is 2 Hz.Ten acquisition experiments are carried out for each group of signals.The number of simulated satellite signals isNs, the total number of signals captured by the acquisition algorithm is, and the number of signals correctly captured is.The statistics ofPDandPFAare calculated as

The results are shown in Fig.4.
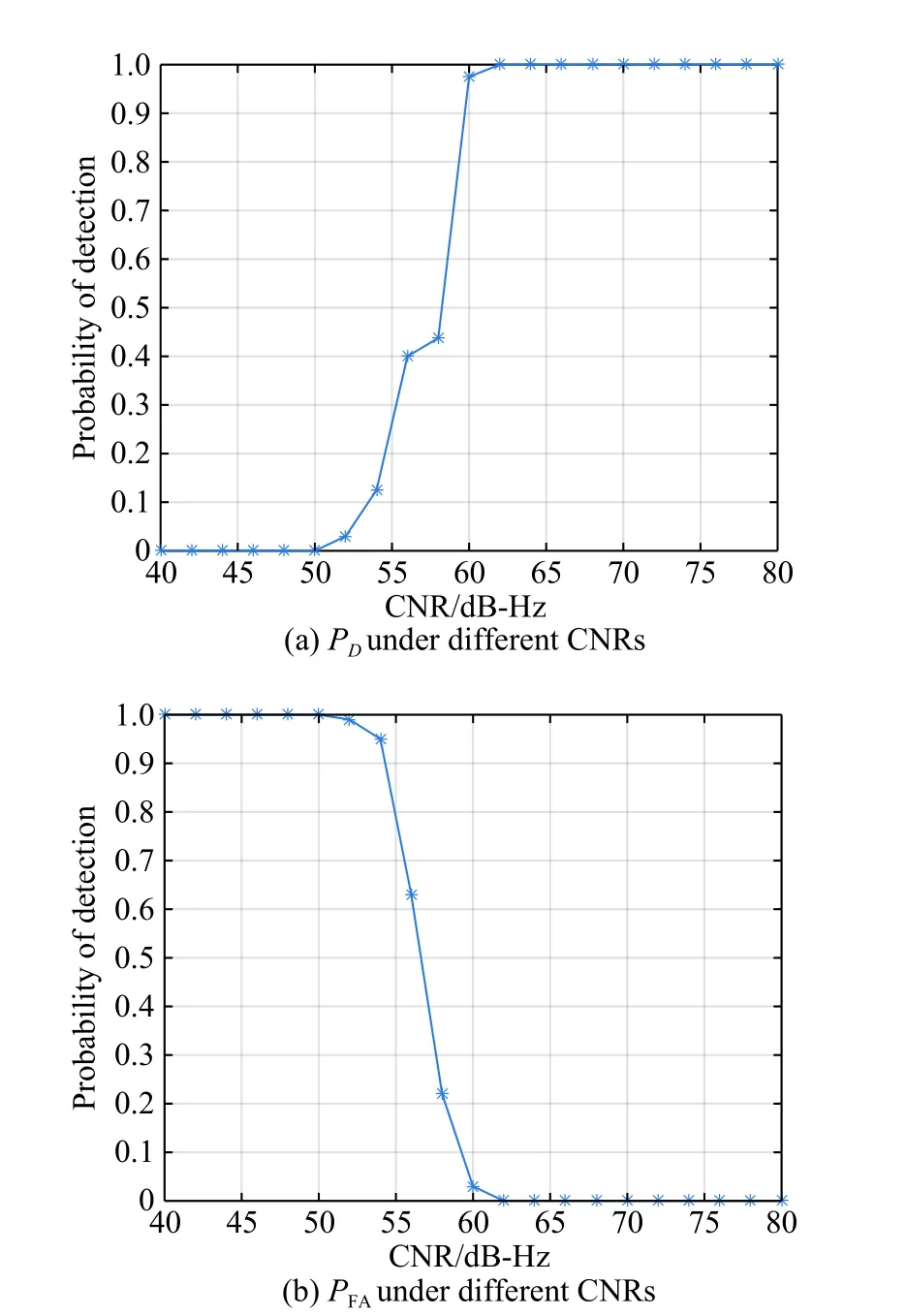
Fig.4 PD and PFA under different CNRs
As Fig.4 shows, without antenna gain, after squaring,even the CNR is improved by accumulation, the signal is drown out by noise and cannot be captured.The bigger the C NR is, the bigger thePDwill be, the smaller thePFAwill be.When CNR is improved to 62 dB-Hz,PDis 1,which means all the target signals are successfully captured.PFAis 0, which means every signal captured can correspond to a specific satellite.In this condition, the acquisition algorithm can successfully capture the GNSS authorized signals.
2.4 Signal tracking
The Doppler frequency shifts of the GNSS signals are changing all the time because of the relative motion between the navigation satellites and the LEO receiver, so the phase locked loop (PLL) is utilized to lock and track the signals.
2.4.1 Analysis of phase error
The main phase error sources of PLL are phase jitter and dynamic stress error.The main error source of phase jitter is the error caused by thermal noise, while other sources are instantaneous or ignorable.The “three-sigma jitter” empirical formula of phase error [23] is given as
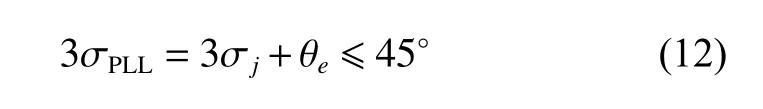
where σPLLis the total phase error, σjis the phase jitter caused by thermal noise, and θeis the dynamic stress error.The tracking threshold is 45?(one-fourth of the phase pull-in range of the PLL discriminator).
The phase jitter error caused by thermal noise can be described by
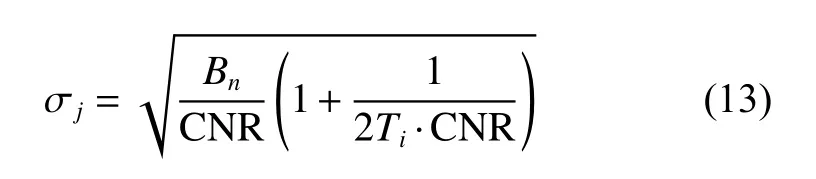
whereBnis the noise bandwidth of PLL,Tiis the coherent integration time.The dynamic stress error of PLL is given as

whereais the radial acceleration, λ is the wave length of the carrier, ωnis the natural frequency of PLL.Substitute(13) and (14) into (12), the detailed expression of phase error is derived as
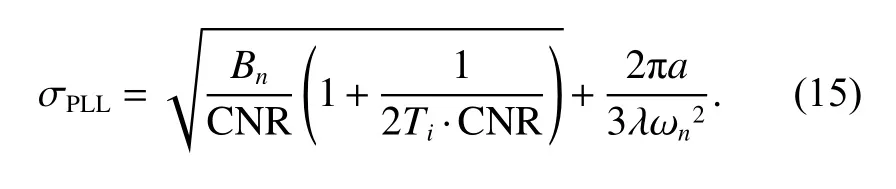
The parameters of PLL directly affect the performance of the tracking loop.TighteningBnand increasingTiwill reduce the effect of white Gaussian noises on the phase error, and then improve the PLL’s ability to continuously track carrier phase.However, in the contrary, the response time of the loop is increased, and the robustness to dynamic change is decreased.According to simulation experiments,Tiis set to be 5 ms to get the optimal performance.When parameters of PLL are fixed, the phase error is positively correlated with the radial acceleration.Whena=13m/s2(the maximum value for the LEO satellite in our scenario), the relationship between noise bandwidth and phase error under different CNRs is shown in Fig.5.
As illustrated in Fig.5, the increase of CNR can significantly reduce the phase error.At a high CNR, the bigger the noise bandwidth is, the smaller the phase error will be.However, the change of phase error is becoming smaller at a high noise bandwidth.As the tracking threshold represented in (12), the phase error should be smaller than 15?, the optimal selection range ofBnis 25?40 Hz.
2.4.2 Isolation of the tracking loop
According to the scenario in this paper, Doppler frequency shifts of all visible navigation satellites are presented in Fig.6.
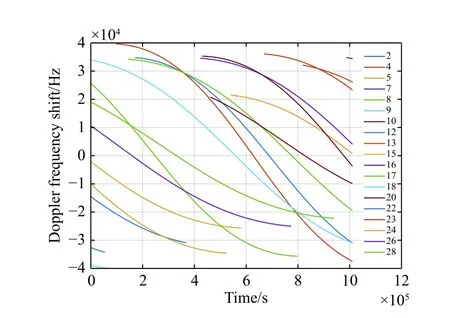
Fig.6 Doppler frequency shifts of all visible navigation satellites
As Fig.6 shows, the Doppler frequency shifts of different satellites overlap from time to time.Without the knowledge of the pseudo-code, carriers with similar frequencies will affect the tracking loop, which lead to a large tracking error or even the loss of lock.The Bode diagram of PLL is shown in Fig.7.
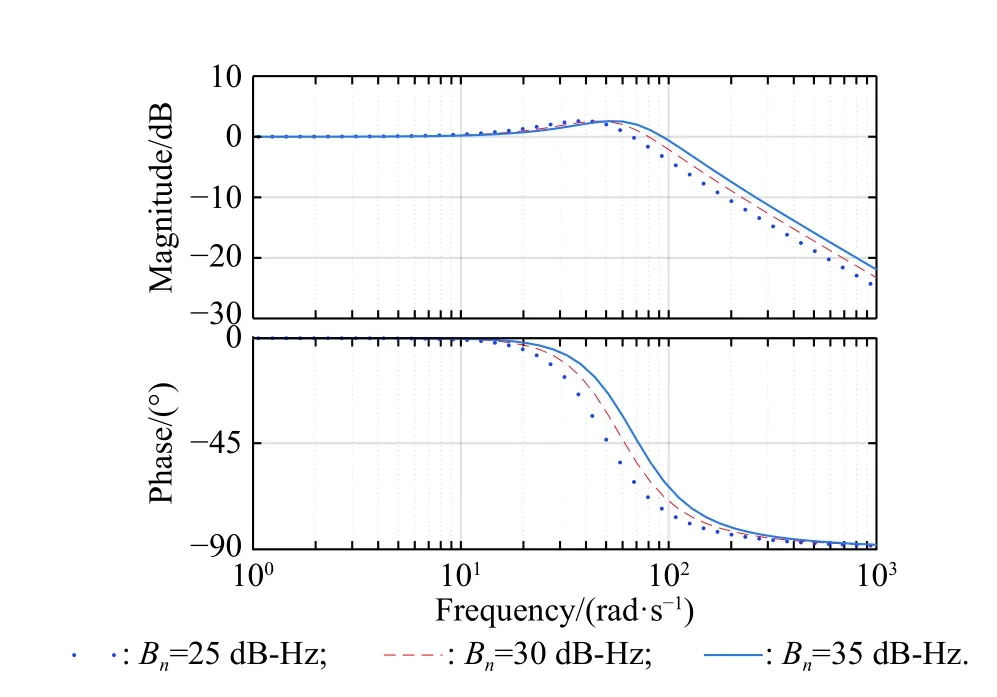
Fig.7 Bode diagram of PLL
The amplitude-frequency curve shows the frequency point at which the gain starts to roll off (called cut-off frequency).PLL has a suppression on the signals whose frequency is different from the target carrier.The bigger the difference is, the more effective the suppression will be.When the signal strength is reduced by 10 times, the effect of other signals on the loop can be ignored.The magnitude correspondingly can be calculated as 20log(1/10)=?20dB .The frequency corresponding to ?20dB is about 600Hz.Therefore, in order to avoid the interference of carriers with similar frequencies, PLL stops the tracking of the carriers when the frequency difference between them is within 600 Hz.
3.Recognition of navigation satellites
All navigation satellites are numbered with a PRN number which uniquely identifies the ranging codes that a satellite uses.However, now that the pseudo-code is eliminated by the squaring method, the carriers reconstructed are distinguished from each other by their frequencies, the traditional pseudo-code matching method to recognize the navigation satellites is no longer available.In this paper a method based on Doppler frequency shift is utilized.The measured Doppler frequency shift can be written as
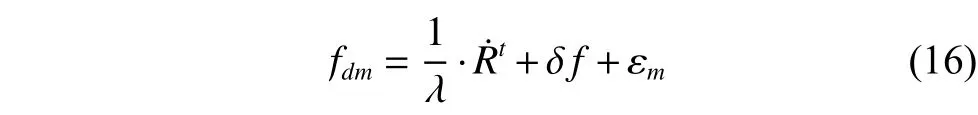
whereRtis the true geometric distance between navigation satellite and LEO satellite, λ is the wave length, δfis the clock frequency offset of the GNSS receiver, and εmis the measurement error.
The prior value of Doppler frequency shift can be calculated as
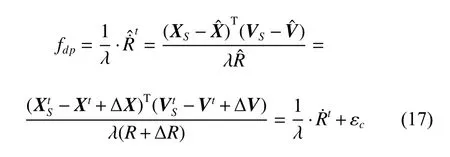
whereXSandVSare the position and velocity of the navigation satellite, which can be known from ephemeris.The ephemeris is calculated and uploaded from the ground.andare the estimated position and velocity of the LEO satellite, which are propagated according to the dynamic equations.are the truth values, ΔX, ΔV, ΔRare the error terms, εcrepresents the deviation caused by the orbit error.Comparing (16) with(17), it can be known that the difference betweenfdmandfdpincludes δf, εmand εc.εmand εcare both within a few tens of Hertz, which is much less than δf.
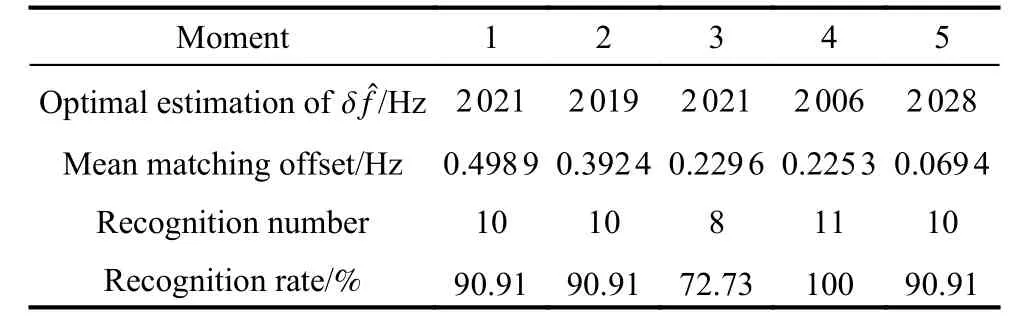
Assume that there areMvisible navigation satellites,both the prior value of Doppler frequency shifts and the measurement are sorted.As Fig.8 shows, if εmand εcare not in the consideration, the difference betweenfdmandfdpis just δf, which is the same in all channels.
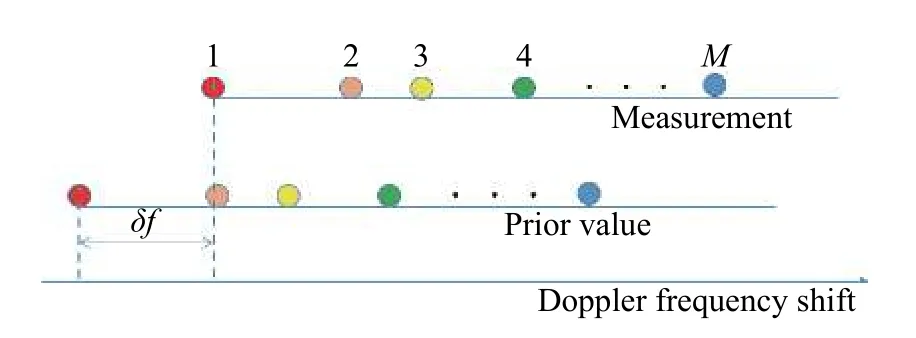
Fig.8 Relationship between the prior of Doppler frequency shift and the measurement
An approximation of clock frequency offsetis introduced as an overall offset.is added tofdp, so thatfdmandfdpcan correspond to each other.Then the differences between two sets of frequencies for every satellite are calculated, the mean value of them is
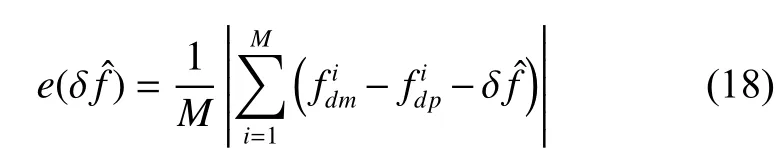
whereeis called the mean matching offset,iis the number of GNSS satellites.By performing a searching method fora series ofecan be obtained.Whenegets to the minimum, the correspondingis considered to be the optimal estimation.However, since thateis the mean matching offset, for a specific satellite, the matching offseteimaybe huge.Ifeiis big enough, the matching results are unconvinced.Thus a thresholdetis set to ensure the matching is accurate.For a specific satellite, the following equation should hold:
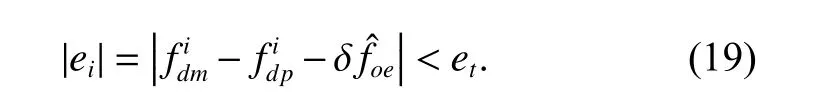
If a carrier frequency does not satisfy (19), the carrier is removed and the corresponding measurements are not used in orbit determination.With a wide searching range,it will take a lot of time using the serial search method to find out the optimal estimation of δf.A dichotomy method is utilized to improve the efficiency.Two possible situations of dichotomy are shown in Fig.9.
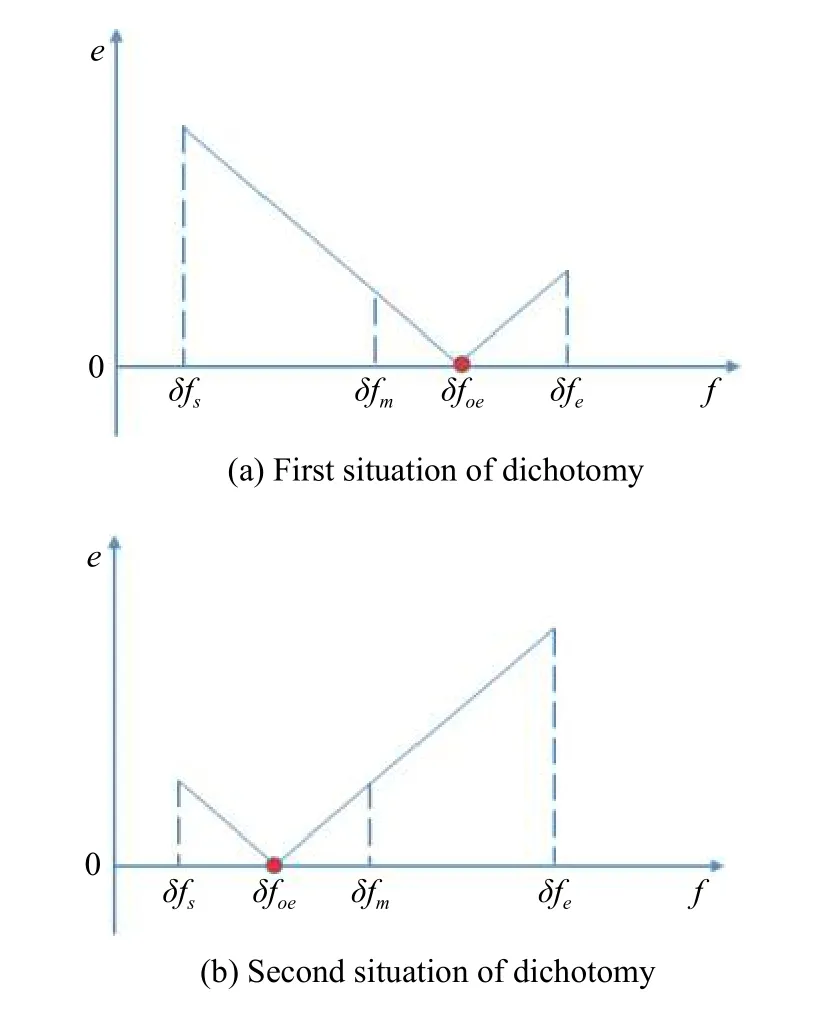
Fig.9 Two possible situations of dichotomy
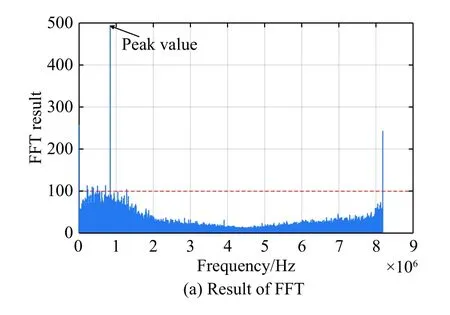
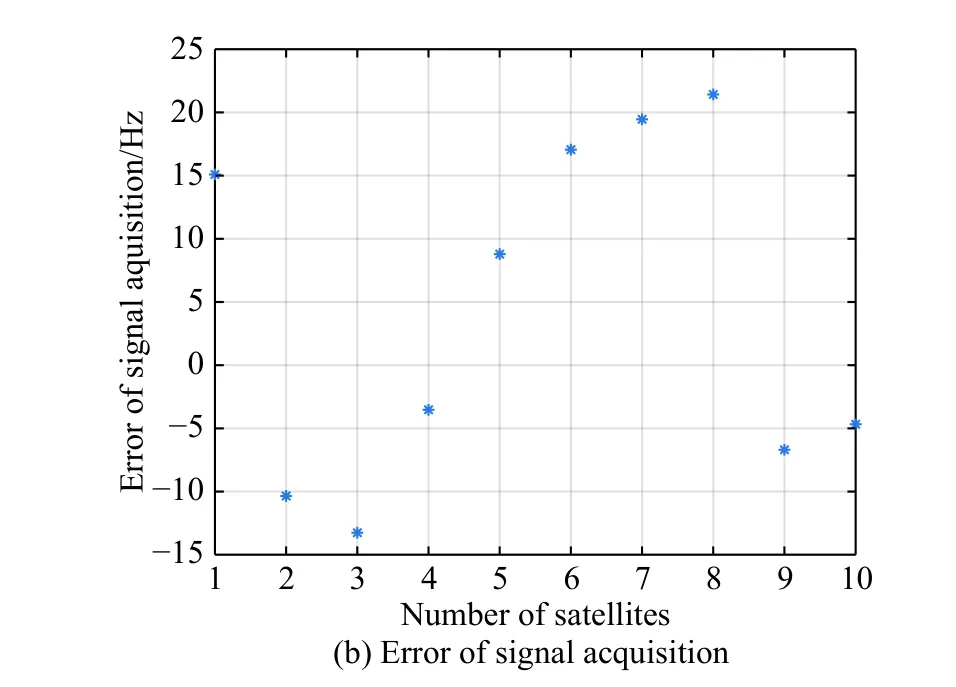
Assume that the searching range is [δfs,δfe], and it is divided into two ranges equally, that is [δfs,δfm],[δfm,δfe].δfmis calculated as
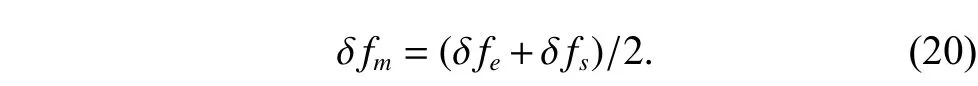
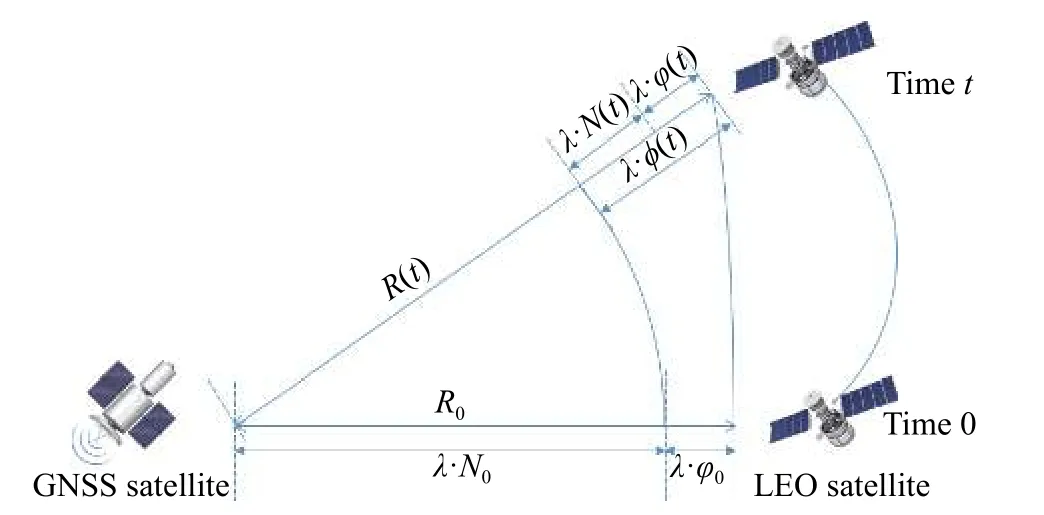
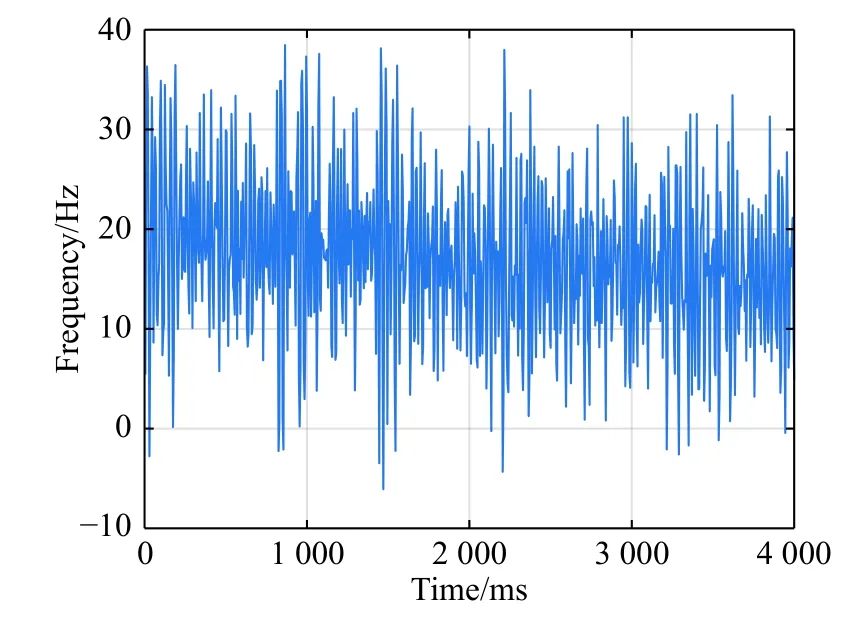
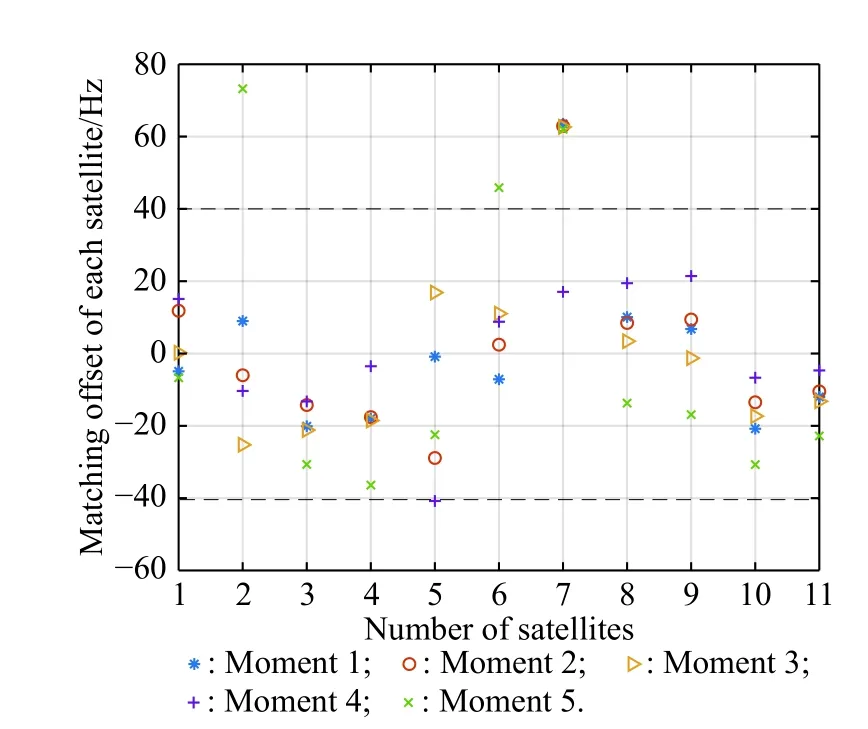
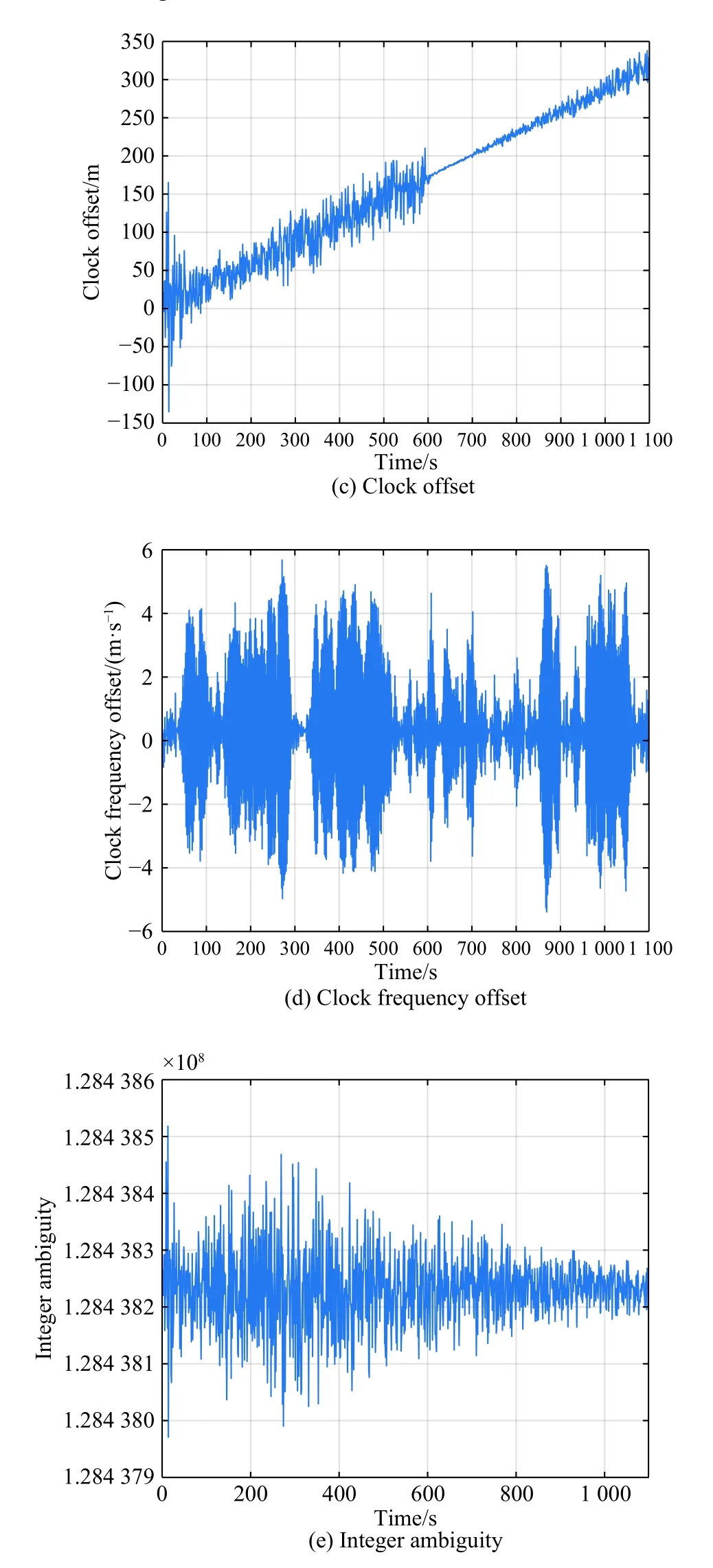
The optimal estimation of δfthat makeseminimum will be in one of the ranges.Calculatee(δfs) ande(δfe)according to (18).Ife(δfs)>e(δfe) , the range [δfs,δfm]will be abandoned, and δfmwill replace δfs.Ife(δfs) A real precise orbit modeling should take into account additional gravitational and nongravitational perturbations.In general, the accelerations acting on the satellite consist of the geopotential gradient, third-body gravitational attraction of the sun and the moon, solar radiation pressure, and atmosphere drag, if no active orbital maneuver is being performed.In this paper the satellite dynamical model is described in the Earth center Earth fixed (ECEF)coordinates.The state vector, including the position and velocity vectors, can be represented as A simplified dynamic model is applied, which can meet the requirements of orbit determination in our scenario.The dynamic model considering J2 perturbation for orbit propagation is described as whereris the geometric distance from the LEO satellite to the Earth center.(x,y,z) is the position of the LEO satellite, μ is the geocentric gravitational constant, ω is the Earth rotation angular velocity.J2is the coefficient of J2 perturbation.The un-modeled perturbation accelerations εx, εy, εzare assumed to be Gaussian white noises and considered as process noises in EKF design. The phase measurement can be regarded as the range between the GNSS satellite and the receiver in units of cycles of the carrier frequency [24], but the initial whole number of carrier cycles between satellite and receiver,which is called the integer ambiguity, is not measurable.The phase measurement model is shown in Fig.10. Fig.10 Phase measurement model The measurement equation is given as where δtis the clock offset, c·δtis the range error caused by clock offset, υ is the measurement error,N0is the initial integer ambiguity, and it is an unknown constant.The phase measurement φ at timetconsists of two components.φ(t) is the phase of part of a cycle,N(t) is the number of cycles after the carrier has been tracked, and it is automatically counted by the PLL.The accurate estimation of integer ambiguity is critical to the precision of orbit determination. The EKF is the most popular estimation algorithm in practical applications.It is based on a linear approximation to the Kalman filter theory.EKF gives the optimal(with minimum mean square error) solution to the linearized problem, when the error sources are uncorrelated and zero-mean.Thus in this paper EKF is utilized to estimate the orbital parameters, it can satisfy the need of post or real time orbit determination.The discrete nonlinear form of state and measurement equations can be described as whereXis the state vector,Zis the observation vector,WandVare the process and observation noises, they are both assumed to be zero mean Gaussian white noises.Γ is the coefficient matrix ofW.f(·) andh(·) are the process and observation nonlinear functions respectively. Some unknown parameters are added into state variables, so that they can be estimated by EKF in real time.The state vector is described as where c·δtis the range error caused by clock offset, c·δfis the range-rate error caused by clock frequency offset,N1,N2,···,NMare the integer ambiguities for each visible satellite.When calculating the state transition matrix, the state propagation model can be simplified as εfis assumed to be zero mean Gaussian white noise.A Taylor expansion is performed to (26) and the high-order terms are ignored where Φ is the state transition matrix and Φk+1|k=I+A·TD.Iis the identity matrix,Ais the change rate of, notationrepresents the estimation ofX,TDis the discrete time.The process noise and its coefficient matrix are given as Similarly, a Taylor expansion is performed to (23), and the high order terms are ignored, the linearized equation can be written as whereHis the observation matrix and.The signkmeans the discrete moment.After the linearization,the increment of phase measurement equals the product of the observation matrix and the state increment.The detailed description of the observation matrix is derived as whereXS,YS,ZSis the position of the GNSS satellite.The equations of discrete EKF are given [25] as wherePis the error covariance matrix, andKis the gain matrix.Thus, after initialization, the orbital parameters can be estimated by EKF according to (31).If sufficiently good initial values are provided, EKF can reach convergence in only a few iterations. In order to verify the feasibility of the technologies proposed in this paper, a semi-physical simulation experiment is carried out.A schematic representation of the experimental equipment is shown in Fig.11.GPS L1 signals are utilized to verify the method proposed in this paper.The navigation signal simulator cannot generate authorized code, and the civil code is chosen to replace it.The differences between civil code and authorized code are the pseudo code and the way of modulating, but after squaring, the unmodulated carriers are the same.The pseudo-code modulated on the carrier is considered to be unknown.The carrier of authorized signals can be fully recovered when the CNR is greater than 62 dB-Hz.The greater the CNR is, the higher the accuracy of signal acquisition will be. Fig.11 Equipment for semi-physical simulation experiment The experimental platform consists of a navigation signal simulator, an immediate frequency (IF) signal sampler and a navigation computer.The navigation signal simulator can generate and export GNSS L1 signals according to the scenario settings.Navigation signals are received by IF signal sampler, and then down-converted into IF signals in radio-frequency channel.All the methods proposed in this paper are evaluated by using the software module on the navigation computer.The navigation software integrates the carrier recovery model, the orbital dynamics, the phase measurement model, and the developed estimator.The composition and function of the experimental platform are shown in Fig.12. Fig.12 Composition and function of experimental platform The detailed signal processing is shown in Fig.13. Fig.13 Detailed signal processing on computer Some additional operations are performed for long-term experiments.In order to indicate whether the navigation signal disappears or a new signal appears, two operations including unlock judgment and new satellite detection are carried out simultaneously, before the measurement information is used to update the state variables.Fig.14 is an example of losing lock, it represents the local frequency of PLL, and it has been adjusted to near 0 so that we can clearly observe its variation.In order to effectively judge if the signal loses lock, a method based on stability detection of local frequency is utilized [26]. Fig.14 An example of losing lock As we can see from Fig.14, when the signal is continuously tracked by PLL, the local frequency will fluctuate within a certain range.However, when the signal loses lock, the local frequency will quickly diverge.Assume that the local frequency of PLL at timetisFt, the maximum error of signal tracking is εfmax.After five times, if the carrier is still tracked by PLL, the following equation should hold: Five continuous integration times are tested.If all the results do not satisfy (32), the signal is considered to be out of lock.And when the LEO satellite orbits in the space, new navigation satellites come into view at times.According to the positions of navigation satellite and LEO satellite, it can be judged that which navigation satellites are visible at current moment.If a new satellite is detectable, the signal acquisition algorithm is carried out to capture the new GNSS signal. The squaring method eliminates the pseudo-code and data code, so theoretically there is no limit to the data length participating in signal acquisition.However, if the data length is too long, the calculation amount will be too large because the sampling ratefsis very high.And the measurement of Doppler frequency shift will be inaccurate because it changes with time.The data length is set as 80 ms, the signal strength is increased by 20 dB in the experiments. The frequency resolution of FFTRFFTgreatly affects the accuracy of signal acquisition.RFFTcan be easily calculated by whereSFis the size of FFT, it is the length of data block,and it is also equivalent to the number of frequency bins that will be created.Each bin represents the amount of energy that the signal has at that particular frequency.RFFTis the difference in frequency between each bin, and thus set a limit on how precise the results can be.The smaller theRFFTis, the higher the accuracy will be.The most intuitive way to decreaseRFFTis to increase the length of data block.However, the accumulation timesLwill be reduced simultaneously in this way.The signal strength is not increased enough, which may cause that some signals cannot be captured.Another method called“zero padding” is applied to solve the problem.Zero padding involves appending some zeros to the end of a signal in time domain.“0” can be considered as the collection of signals, whose frequency is arbitrary and amplitude is 0.In this wayRFFTis decreased, the accuracy of FFT is improved.The amplitude of the FFT result is decreased overall, which will not affect the detection of the peak amplitude.Finally, the length of data involved in signal acquisition is 80 ms, the length of the data block is set as 4 ms.The threshold of signal acquisition is set as 300.TheRFFTis decreased to 40 Hz after zero padding.The result of FFT and the error of signal acquisition is shown in Fig.15. Fig.15 Result of FFT and error of signal acquisition The result of FFT represents the spectrum of the signal at discrete frequencies.As Fig.15 shows, after accumulation, the amplitude spectrum of the target frequency is much bigger than the other frequencies’, so it is easy to detect.The Doppler frequency shift can be calculated by(10).The error of signal acquisition is within 40 Hz. The parameters of the tracking loop are set as follows:the noise band width (NBW) is set as 25 Hz, the natural frequency of the loop ωnis calculated by an empirical formula ωn=Bn/0.53, the coherent integration time is 5 ms.Because the tracking results of other carriers are similar, only one of the tracking errors is illustrated in Fig.16. Fig.16 Error of tracking results The tracking error is the difference between the frequency of the local signal and the prior frequency of the input signal, and it reflects the precision of tracking. The phase detector of PLL keeps comparing the phase of the local signal and the input signal, adjusting the voltage-controlled oscillator (VCO) to change the frequency of the local signal, thus PLL completes the tracking of the input signal.As Fig.16 shows, PLL realizes the tracking of the carrier without the help of pseudocode, the tracking error is within 40 Hz. According to (19),eishould be less than the maximum tracking error, so the thresholdetis set as 40 Hz.GNSS receivers are equipped with quartz crystal clocks that are less stable than the atomic clocks used in navigation satellites.is changing with time, a rough prior value is estimated according to the calibration error of GNSS receiver clock, which provides the basis for selection of the searching range.The searching range ofis set as[1000,3000]Hz.Dichotomy is utilized to improve the efficiency, the termination condition isfe?fs<1Hz.The recognition algorithm is carried out at five different moments.The matching offsets of all visible satellites are calculated according to (19) after the optimal estimation ofis obtained, which are represented in Fig.17. Fig.17 Matching offsets of all visible satellites As can be seen from Fig.17, in most cases, the matching offsets are within ±40 Hz, which means that most satellites can be recognized.Only a few matching offsets are beyond the threshold, the corresponding satellites are considered not recognized in that moment.The matching results and statistical information are recorded in Table 1. Table 1 Matching results and statistical information The design of the constellation makes it possible that there are always about 10 visible satellites from any point at the LEO space at any time.The average recognition rate is 89.1%, which means that in most cases, eight or more navigation satellites can be correctly recognized,and it is enough for orbit determination. The scenario starts from the epoch 7 June 2019,00:00:00(UTC) and covers 1100 s.The initial orbit parameters are as follows: the semi-major axis is 6871 km(the orbital altitude is about 500 km), the eccentricity is 0.001, the orbital inclination is 0°, the right ascension of ascending node is set to be 0°, the argument of perigee is set to be 0°, and the true anomaly is set to be 0°. In the algorithm of EKF, J2 perturbation is considered in the dynamic model.The initial position and velocity errors are set as 100 m, 100 m, 100 m, 0.2 m/s, 0.2 m/s and 0.2 m/s.The 4th order Runge-Kutta numerical integration method is utilized for orbit propagation, the orbital integral step is 1 s.The process noise covariance matrixQkis set to diag[(1e?9),(1e?9),(1e?9),(c·1e?9)2], the observation noise covarianceRkis set to diag[(1e?3)2].The initial integer ambiguities are calculated according to the initial positions of LEO satellites and GNSS satellites.Initial clock offset and clock frequency offset are set to be 0.The results of orbit determination are presented in Fig.18. Fig.18 Results of orbit determination As presented in Fig.18, the EKF can quickly converge.The RMS errors of position are 19.62 m, 20.55 m, 5.69 m inX,Y,Zdirections.The RMS errors of position are different with time.For example, the RMS errors of position inYdirection are 29.03 m during 200?598 s, 4.49 m during 599?857 s, and 12.75 m during 858?1100 s.This is because the number of navigation satellites changes with time, and different navigation satellites have different contributions to the improvement of precision because of the geometric dilution of precision (GDOP) effect.A poor GDOP lowers the quality of positioning by meters.The RMS errors of velocity in three directions are 0.12 m/s, 0.12 m/s and 0.13 m/s respectively.The clock frequency offset fluctuates around 0, the clock offset increases with time almost linearly.The range error caused by the clock offset is about 0.29 m in a second.The integer ambiguities of all visible satellites are estimated by EKF.The standard deviations of integer ambiguity are 80.6 cycles during 0?599 s, and 38.9 cycles during 600?1100 s, and each cycle will bring error (about 0.24 m) to the position. The method proposed in this paper successfully realizes the navigation via GNSS authorized signals, which can be regarded as a special method to realize NAVSOP.The experimental results are in agreement with theoretical analysis.This paper provides an alternative navigation method in special occasions, which enables satellites to provide stable and long-term services for civilian users.The amount of calculation severely restricts the improvement of precision.More intelligent and faster technologies should be explored to complete the reconstruction of the carrier and calculate the orbit parameters.4.Orbit determination based on carrier phase measurements
4.1 Dynamic model

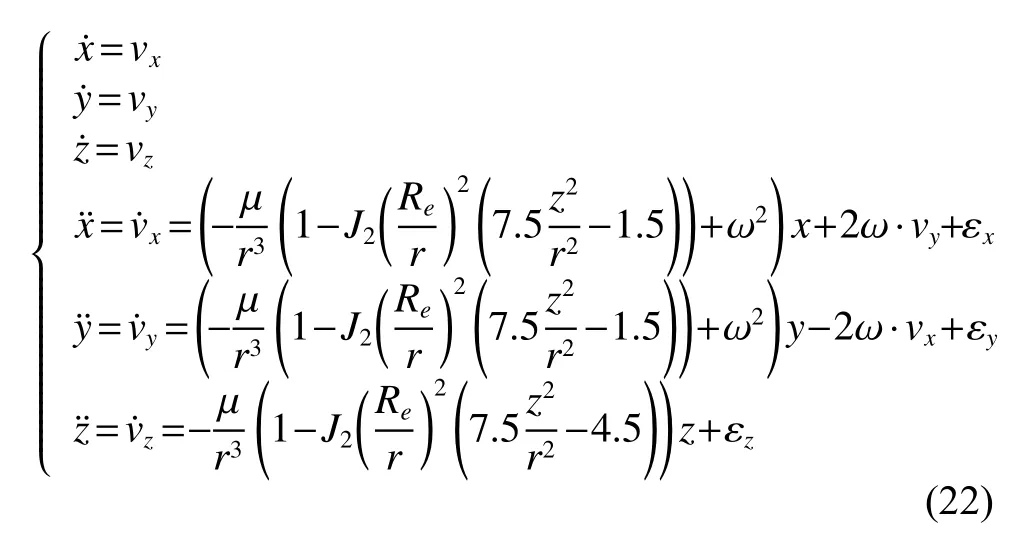
4.2 Phase measurement model
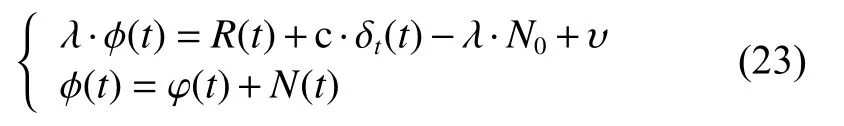
4.3 Design of EKF
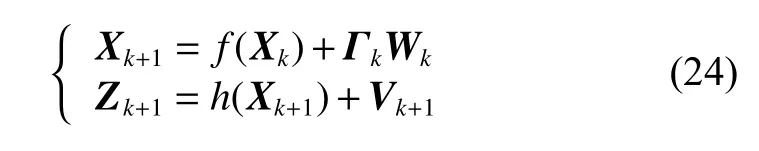
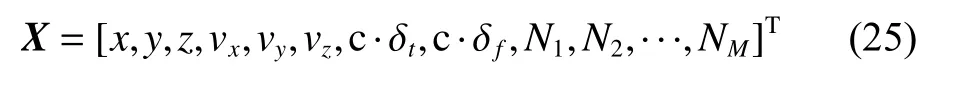
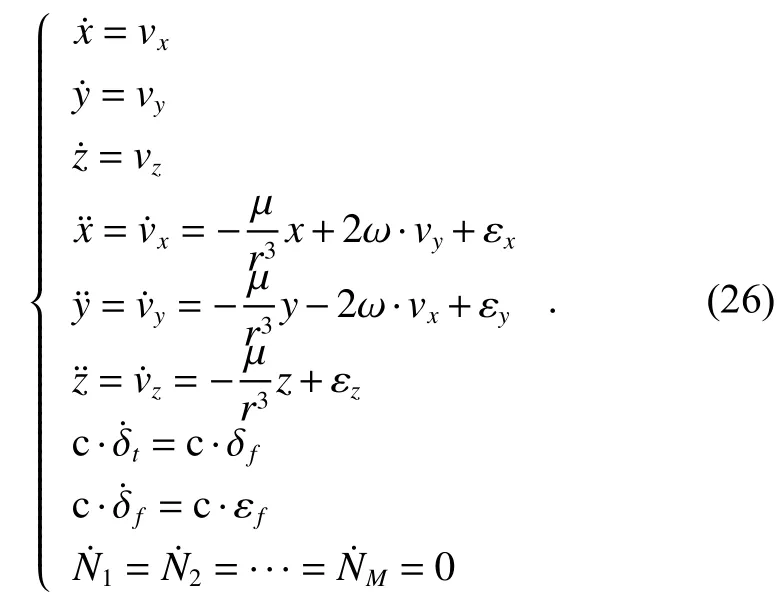
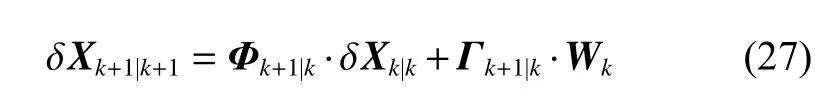
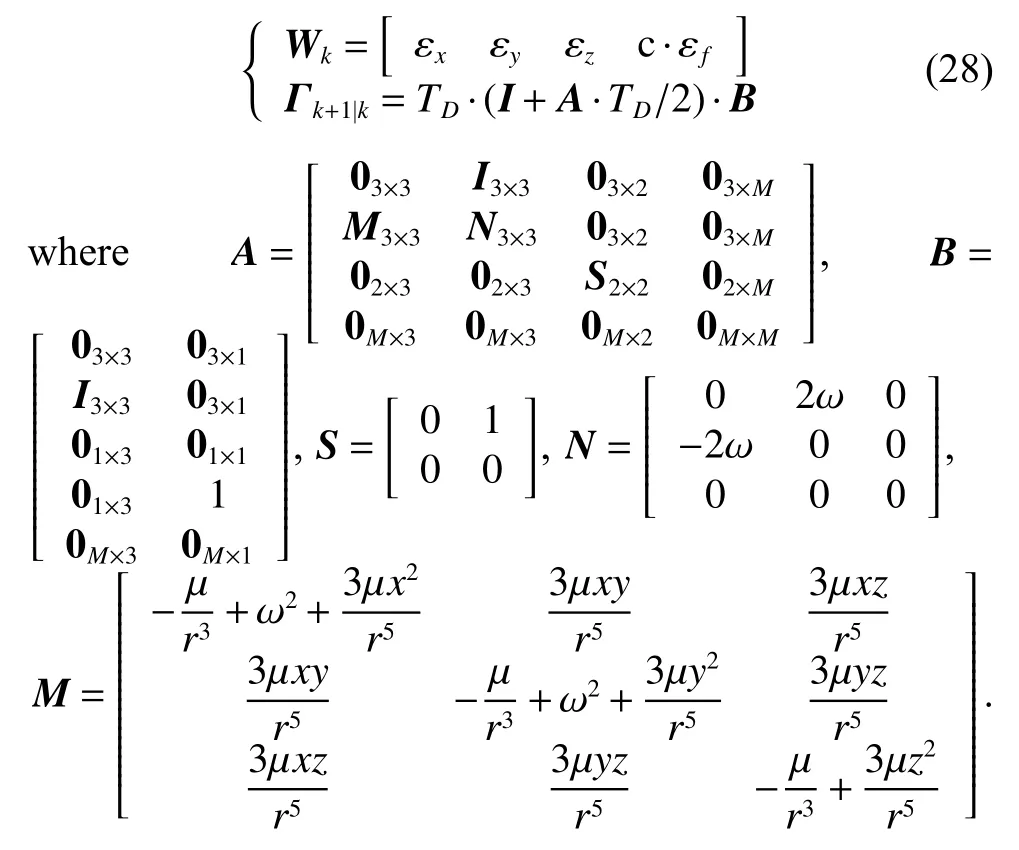
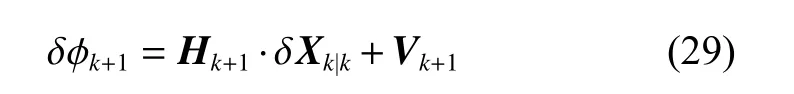
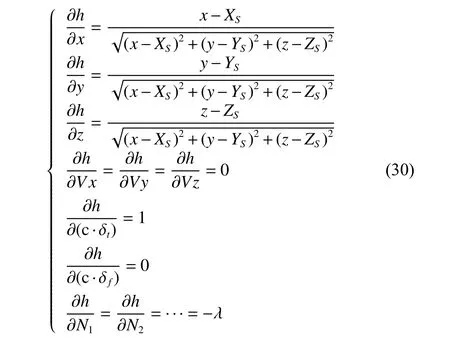
5.Experimental results and analysis
5.1 Experimental design

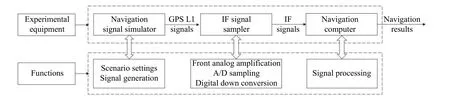
5.2 Pre-processing strategy
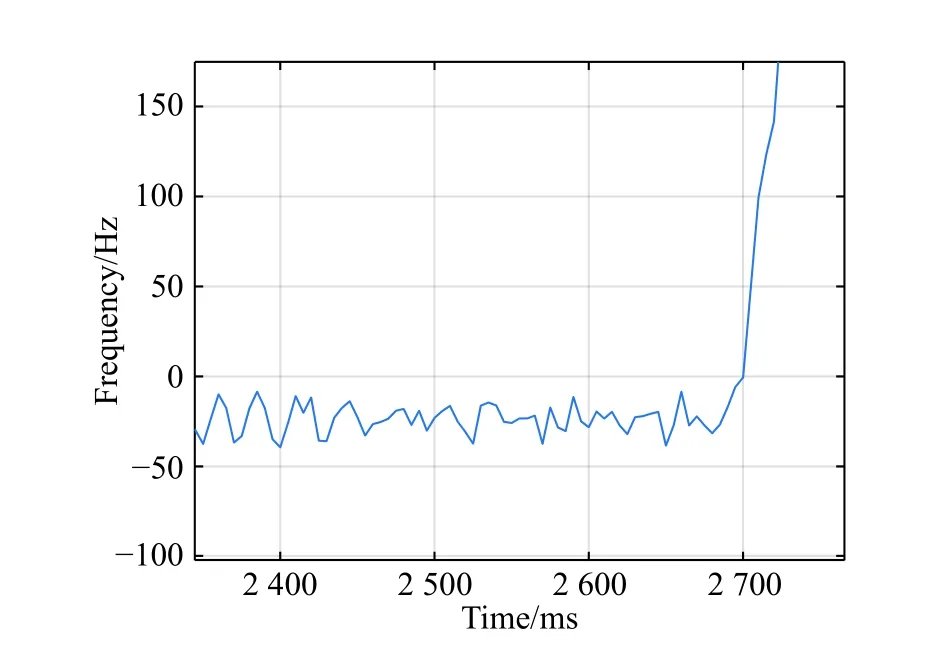
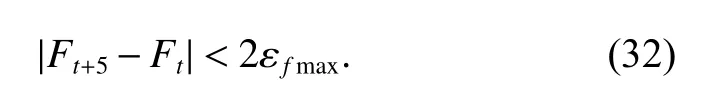
5.3 Results of carrier recovery and analysis

5.4 Results of navigation satellite recognitionand analysis
5.5 Results of orbit determination and analysis
6.Conclusions
 Journal of Systems Engineering and Electronics2021年5期
Journal of Systems Engineering and Electronics2021年5期
- Journal of Systems Engineering and Electronics的其它文章
- Belief reliability modeling and analysis for planetary reducer considering multi-source uncertainties and wear
- M-FCN based sea-surface weak target detection
- New Developments on Fault Detection and Diagnosis (FDD) and Fault-Tolerant Control (FTC) Techniques
- Reliability analysis of k-out-of-n system with load-sharing and failure propagation effect
- An iterated local coordinate-exchange algorithm for constructing experimental designs for multi-dimensional constrained spaces
- An integrated simulation system for operating solar sail spacecraft
