高 龍,王麗萍,賈珊珊,羅利萍,邱 芬

(河北師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,河北石家莊 050024)

§1 引言

在單復(fù)變函數(shù)理論中,關(guān)于奇異積分算子性質(zhì)的研究一直是國際上非常活躍的研究課題之一.它在解決復(fù)變函數(shù)的邊值問題上具有重要意義,并且奇異積分也不斷地與其它的數(shù)學(xué)分支交叉融合.例如調(diào)和分析,位勢理論,算子代數(shù),偏微分方程和數(shù)值逼近等.

四元數(shù)是由愛爾蘭數(shù)學(xué)家Hamilton于1843年發(fā)現(xiàn)的,這是19 世紀代數(shù)學(xué)最大的事件之一.四元數(shù)分析是現(xiàn)代分析的重要分支,它推廣了平面復(fù)數(shù)系結(jié)構(gòu).其主要研究定義在R3或R4空間,取值于H(R)或H(C)空間上的函數(shù).國內(nèi)外許多學(xué)者對四元數(shù)分析與Clifford分析中一些奇異積分算子的性質(zhì)和應(yīng)用進行了深入研究.例如Spr¨ossig[1-3],Adler[4],Du[5-6],Qiao[7-9],Wang[10-14]等等.Helmholtz方程是高維空間一類重要的偏微分方程,是Laplace算子的一種自然推廣.其中α-超全純Cauchy-Riemann算子是Helmholtz算子的分解.Timeharmonic Maxwell方程是由Maxwell于1865年提出的.它是描述電磁現(xiàn)象的偏微分方程組.此外Time-harmonic Maxwell方程的解滿足齊次Helmholtz方程,因此這兩類方程之間存在密切的聯(lián)系.許多學(xué)者研究了與Helmholtz方程和Time-harmonic Maxwell方程相關(guān)的一些問題.例如Mclntosh和Mitrea[15-16]討論了與Helmholtz方程和Maxwell方程有關(guān)的一些問題,Schneider和Shapiro[17-18]研究了與Time-harmonic Maxwell方程相關(guān)的Cauchy型積分的一些性質(zhì),Abreu-Blaya[19]和Gu[20]研究了與Time-harmonic Maxwell方程和修正的Helmholtz方程有關(guān)的邊值問題.

本文研究與Time-harmonic Maxwell方程有關(guān)的Cauchy型積分算子的一些性質(zhì),結(jié)構(gòu)安排如下: §2回顧有關(guān)四元數(shù)分析的一些基本知識以及與HelmHoltz方程有關(guān)的Cauchy型積分算子的一些結(jié)論. §3介紹N矩陣算子,并研究與N矩陣算子有關(guān)的Cauchy型積分算子的某些性質(zhì).§4介紹與Time-harmonic Maxwell方程有關(guān)的Cauchy型積分算子,此外還研究了它與N矩陣算子有關(guān)的Cauchy型積分算子之間的關(guān)系.最后利用它們之間的關(guān)系,給出了以下三種情況下的與Time-harmonic Maxwell方程有關(guān)的Cauchy型積分算子的H¨older連續(xù)性:兩個點在邊界上;一點在邊界上,另一點在區(qū)域內(nèi)(區(qū)域外);兩點分別在區(qū)域內(nèi)(區(qū)域外).

§2 預(yù)備知識

設(shè)i是C中的虛單位元.它滿足

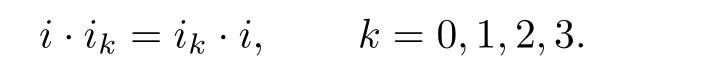
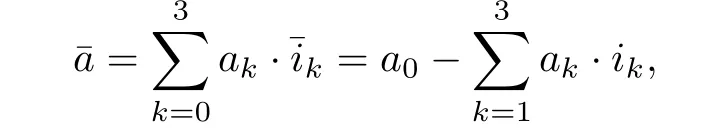
并可定義復(fù)共軛為:

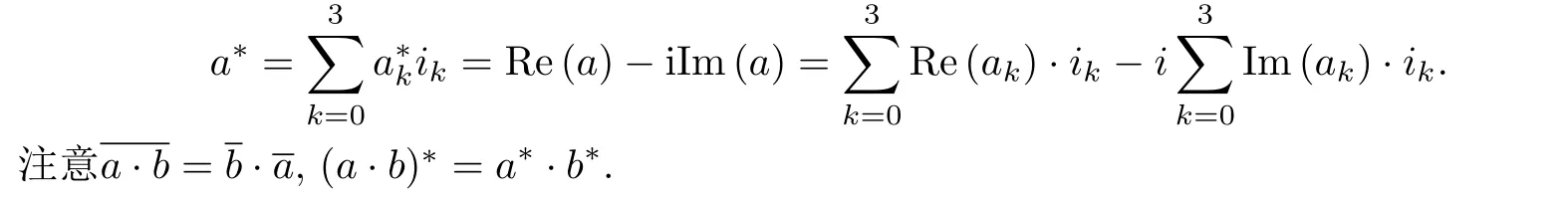
元素a ∈H(C)的模為

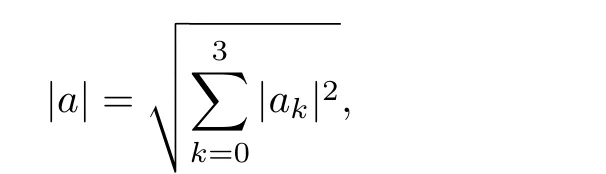
則依據(jù)四元數(shù)共軛可得以下關(guān)系:若H(C)?a=Rea+iIma,則

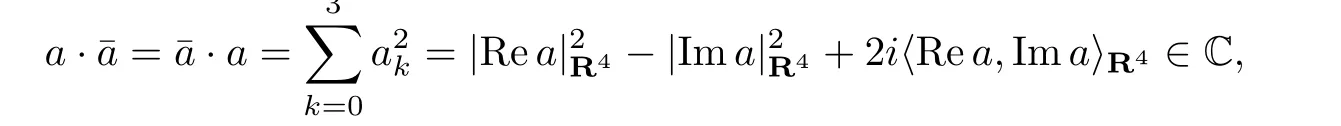
其中〈Rea,Ima〉R4是兩個四維向量的數(shù)量積.

在實四元數(shù)空間中,a·=·a=|a|2.但從上述公式中可以看出,它在復(fù)四元數(shù)空間中并不成立.

為帶有參數(shù)λ=α2的Helmholtz方程的基本解.

則算子Dα的基本解Kα為:

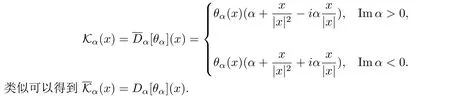
設(shè)f是H¨older連續(xù)函數(shù),則α-超全純Cauchy型積分定義為:

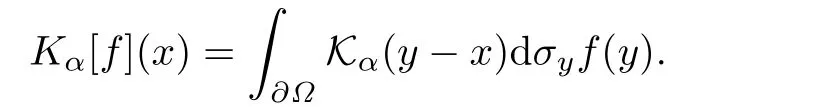
令Ω+=Ω是R3中的有界區(qū)域,其邊界?Ω為緊的Liapunov曲面,定義Ω?=R3(Ω+?Ω).則上述Cauchy型積分的Sokhotski-Plemelj公式為:

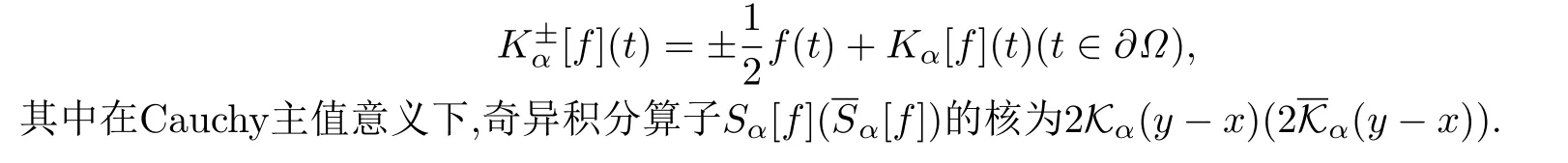
在論文[21]中,有以下結(jié)論:

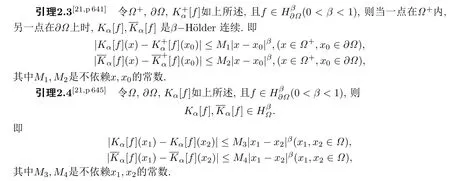
§3 與N 矩陣算子有關(guān)的Cauchy型積分算子

在集合C(1)(Ω,Mat2×2(H(C))) 上考慮下面的矩陣算子:

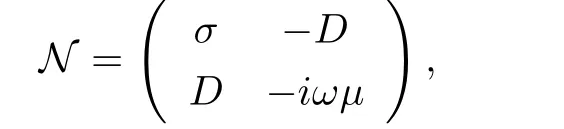
其中α2=iωμσ,Mat2×2(H(C))為元素取值在H(C)中的2×2矩陣集合.

其中“?”表示矩陣乘積.

類似地設(shè)

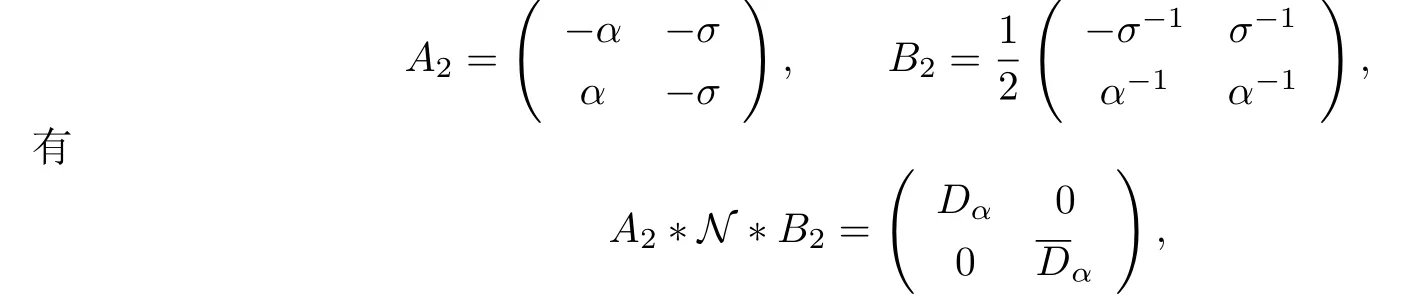
其中矩陣A1,B1,A2,B2都可逆.

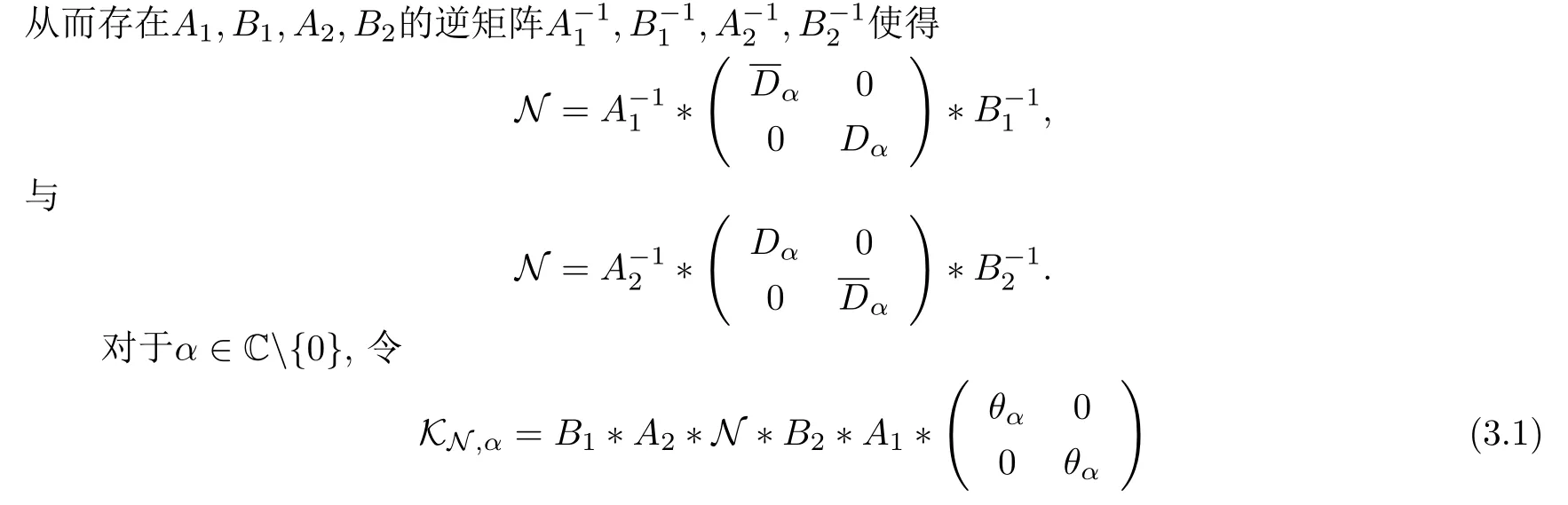
為四元數(shù)Cauchy-Maxwell核,顯然KN,α為N的基本解.

類同于積分表示理論中的Cauchy型積分的定義,帶有四元數(shù)Cauchy-Maxwell核的Cauchy型積分可如下定義:

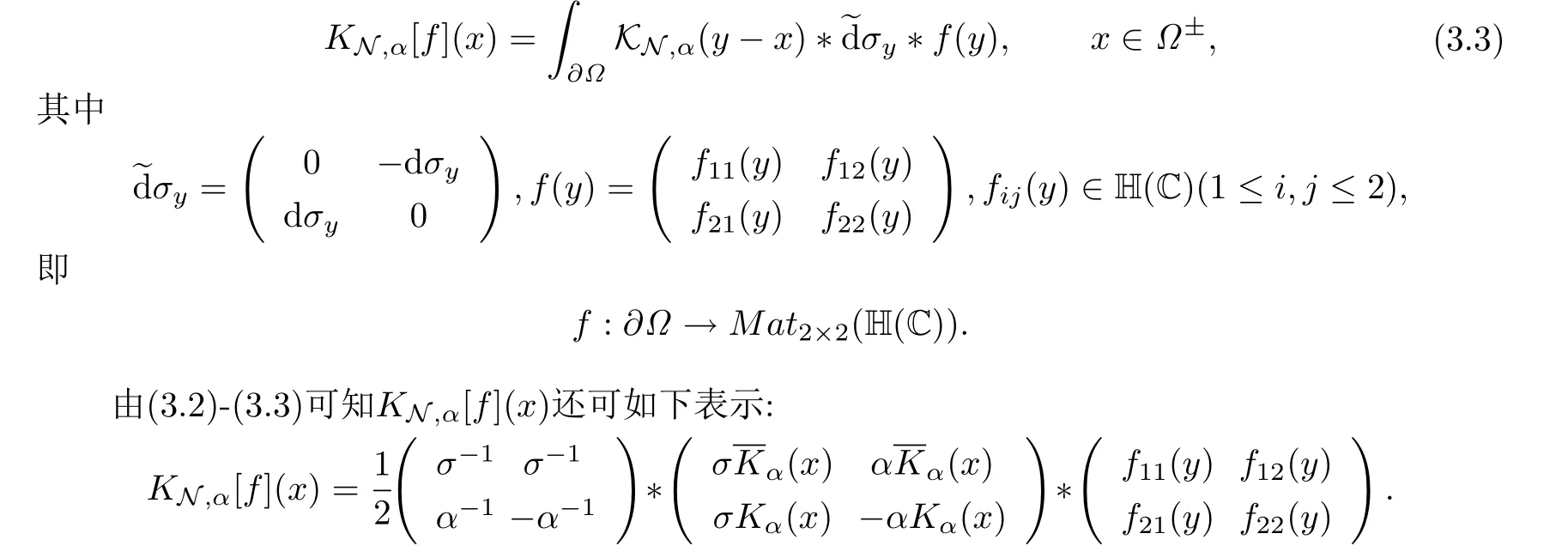
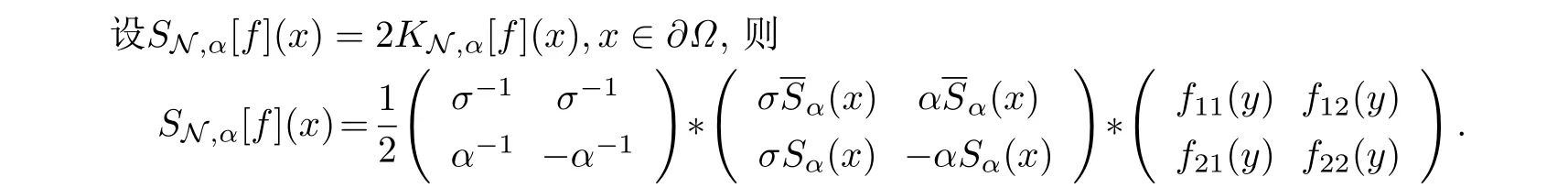
類似地,稱SN,α[f](x)為四元數(shù)Cauchy-Maxwell奇異積分.

定理3.1設(shè)Ω,?Ω,SN,α[f]如上所述,若

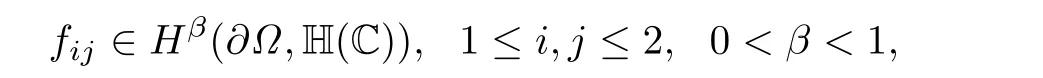
則SN,α[f]∈Hβ(?Ω,Mat2×2(H(C))).

證對?x1,x2∈?Ω,有

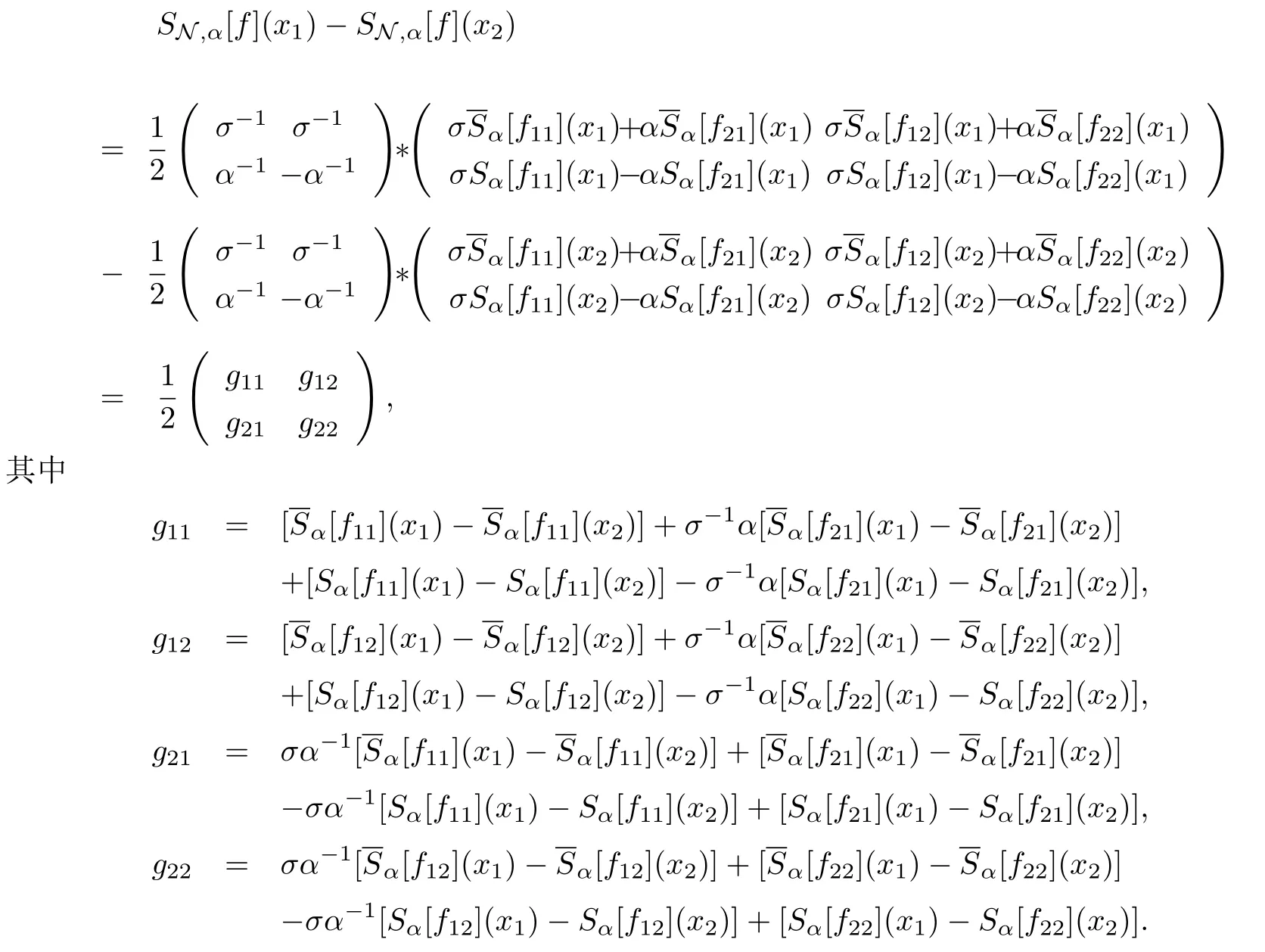
并且由引理2.1知

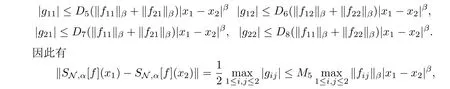
其中M5=max{2D5,2D6,2D7,2D8}.

所以SN,α[f]∈Hβ(?Ω,Mat2×2(H(C))).

注3.1根據(jù)定理3.1的結(jié)論,顯然有SN,α[f]∈Hβ(?Ω,Mat2×2(H(C))).

定理3.2設(shè)Ω,?Ω,KN,α[f],SN,α[f]如上所述,若fij ∈Hβ(?Ω,H(C)),1≤i,j ≤2,0<β <1,則

定理3.5設(shè)Ω,?Ω,KN,α[f]如上所述,若

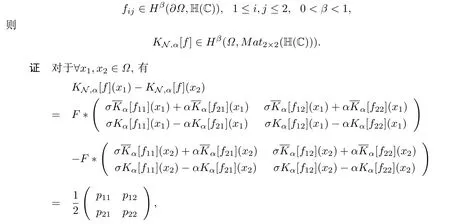
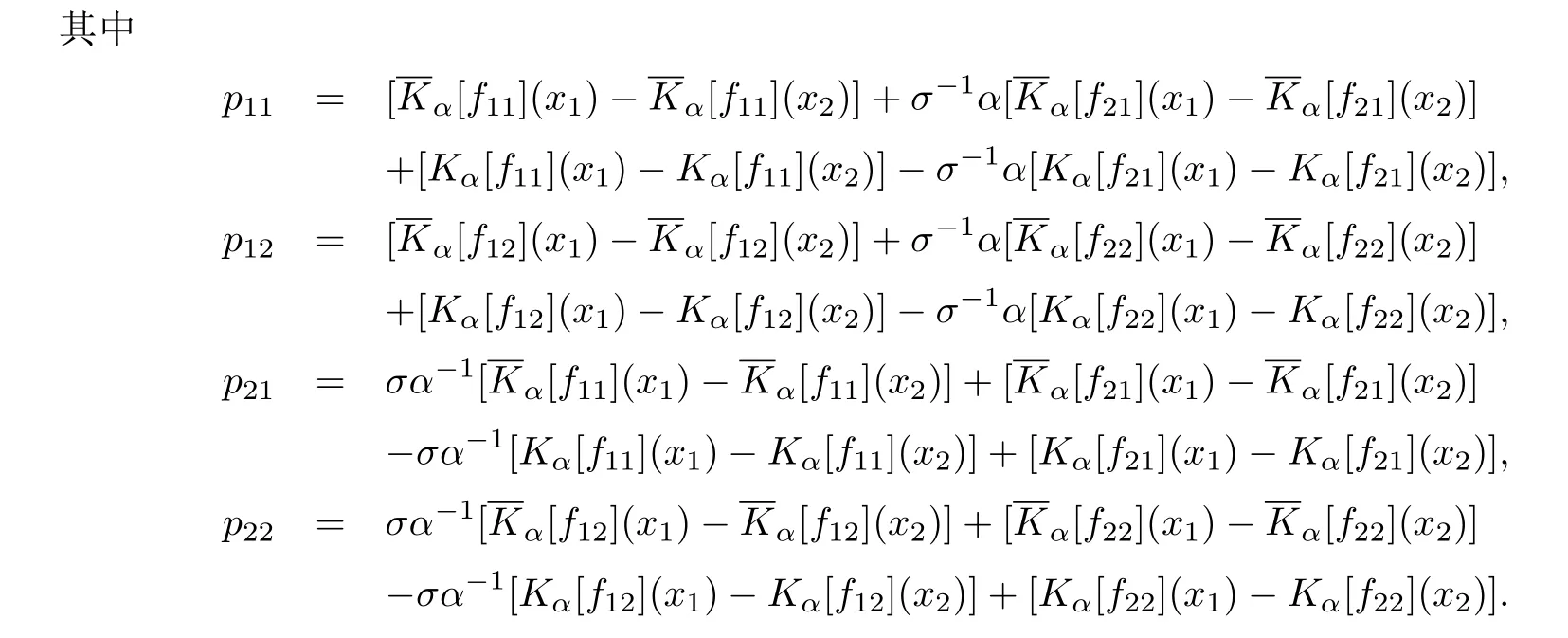
并且由引理2.4有

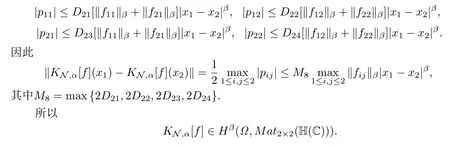
§4 與Time-harmonic Maxwell方程有關(guān)的Cauchy型積分算子