施 云

(浙江科技學(xué)院理學(xué)院,浙江杭州 310023)

§1 引言

Araklov在緊Riemann面上利用Bergman度量的Green函數(shù)構(gòu)造了一個共形不變度量[1].Leutwiler在Rn的局部鄰域上構(gòu)造了一個類似的共形不變度量[2].Harbermann和Jost在數(shù)量曲率為正的局部共形平坦流形上構(gòu)造了一個標(biāo)準(zhǔn)共形不變度量[3-4].在此之后,王偉構(gòu)造了CR流形上的Yamabe算子,數(shù)量曲率為正的球型CR流形上Green函數(shù),并用此Green函數(shù)構(gòu)造了上述共形不變度量[5].在[6]中,作者研究了四元切觸版本的上述問題,構(gòu)造了四元切觸流形上的Yamabe算子,數(shù)量曲率為正的球型四元切觸流形上Green函數(shù),并用此Green函數(shù)構(gòu)造了一個共形不變張量,證明了該共形不變張量在四元切觸正質(zhì)量猜測成立的情況下是一個共形不變度量.最近此研究推廣到了八元切觸流形上[7].在[8]中還給出了Heisenberg群上鄰域版本的上述共形不變切觸形式,并由此切觸形式構(gòu)造了一個鄰域上的擬雙曲Carnot-Carath′eodory不變度量.

本文利用Paneitz算子對應(yīng)的Green函數(shù)在局部共形平坦流形上構(gòu)造了上述共形不變度量.

§2介紹了Riemann幾何的一些基本概念,給出了Riemann流形上的Paneitz算子以及Q曲率的定義并介紹了[9-10]中給出的Riemann流形上Paneitz算子對應(yīng)的正質(zhì)量定理. §3證明了本文的主要定理,即應(yīng)用Paneitz算子對應(yīng)的Green函數(shù)以及該Green函數(shù)在共形變換下的變換公式,構(gòu)造出一類新的共形不變度量.最后,給出了該共形不變度量的一些性質(zhì).

§2 預(yù)備知識

Q曲率首先在[11]中引入,Chang,Gursky,Yang對4維流形上的Paneitz算子和Q曲率進(jìn)行了深入的研究[12].在此之后,高維流形上的Paneitz算子和Q曲率問題受到越來越多的數(shù)學(xué)家的關(guān)注,成為當(dāng)今共形微分幾何與幾何分析研究的一個重要的課題.更多關(guān)于Q曲率與Paneitz算子相關(guān)的研究參見[13-16]及其參考文獻(xiàn).最近,Q曲率問題還被推廣到了CR流形和四元切觸流形上[17-20].

記(M,g)為n維光滑的緊Riemann流形,φ ∈C∞(M)是M上的函數(shù),于是

稱為Riemann度量g的共形變換.形為e2φg的度量的全體所構(gòu)成的集合稱為g的共形類,記為[g].

對于度量g,

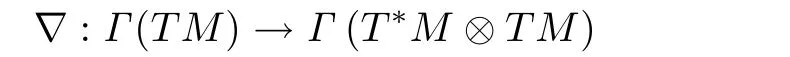
表示相應(yīng)的Levi-Civita聯(lián)絡(luò),這定義了向量空間Γ(TM)=X(M)上的一個滿足

的協(xié)變導(dǎo)數(shù)

令R表示Riemann流形(M,g)上的曲率張量,那么對于任意的X,Y ∈TM,有

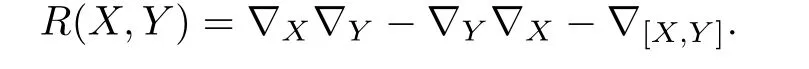
Ricci曲率張量定義為

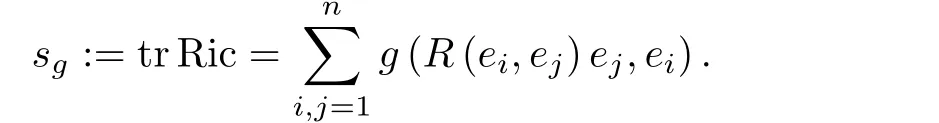
當(dāng)f ∈C∞(M),對于任意X ∈TM,梯度gradg(f)∈X(M)定義為

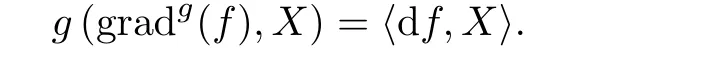
對X,Y ∈TM,f的Hessian形式定義為

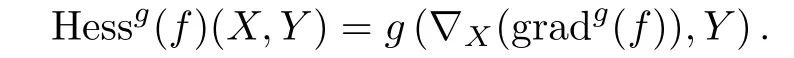
Ricci曲率在共形變換(1)下的變換公式為(參見[16,21])

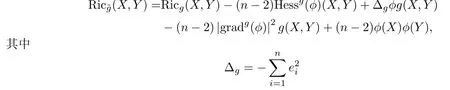
是M上的Laplacian算子.

進(jìn)一步的,可以給出數(shù)量曲率在共形變換(1)下的變換公式(參見[16,21])

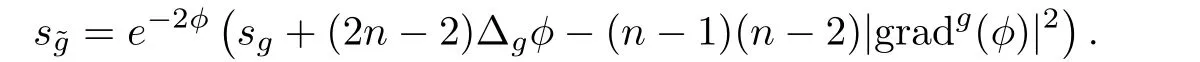
當(dāng)n ≥3時,Schouten張量定義為

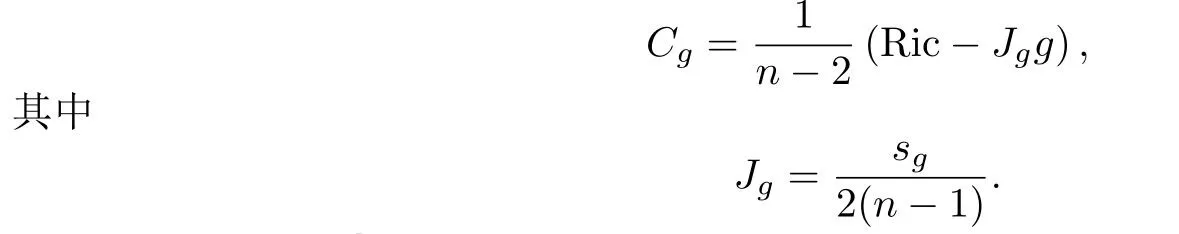
因此有(參見[16,21])

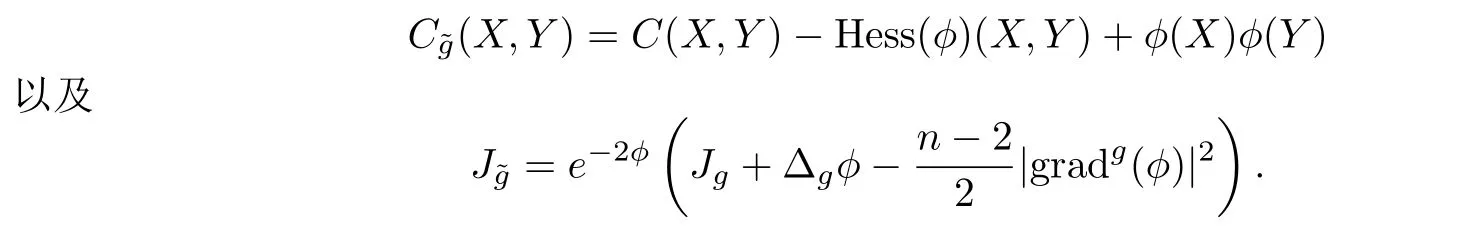
當(dāng)n ≥3,Riemann流形上的Q曲率Qg定義為

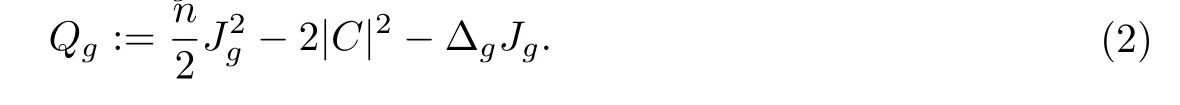
通過簡單的計(jì)算,有

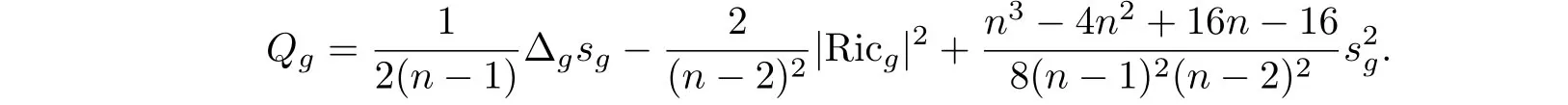
Paneitz算子Pg的定義為

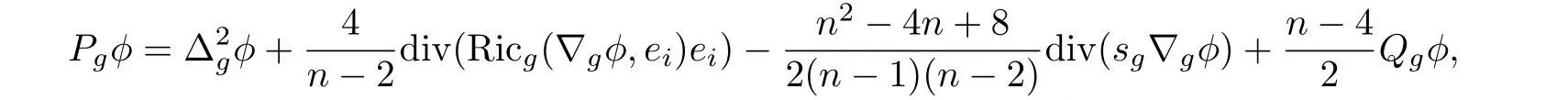
其中?gφ=(e1φ,……,enφ).這是一個共形協(xié)變算子.為了方便計(jì)算,下文中通過適當(dāng)?shù)淖儞Q把共形變換(1)寫成

在該共形變換下,Paneitz算子滿足如下變換公式(參見[10,16])

其中f為任意光滑實(shí)函數(shù).一個連續(xù)的函數(shù)

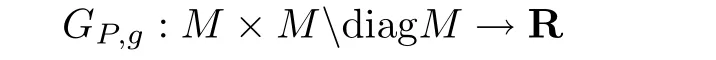
稱為Paneitz算子Pg的Green函數(shù),如果對于任意的u,滿足

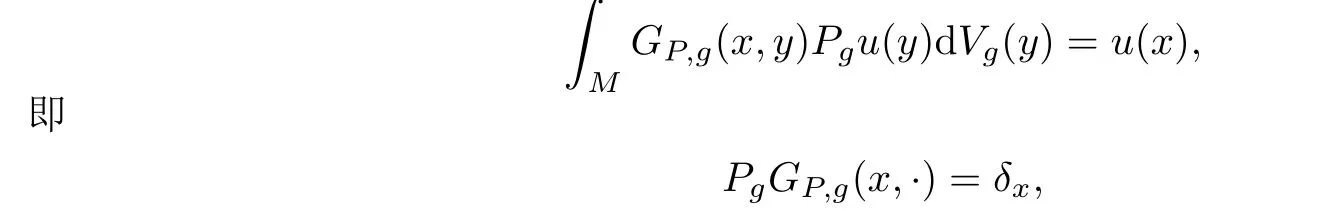
其中δx是在x處的Dirac函數(shù).在共形變換(3)下,有如下Riemann流形上的體積元的變換公式(參見[10])

Green函數(shù)在共形變換(3)下的變換公式如下.

證由體積元在共形變換下的變換公式(5)以及Paneitz算子在共形變換下的變換公式(4),

由Green函數(shù)的唯一性,命題得證.

緊Riemann流形(M,g)(dimM ≥3)的Yamabe算子定義為(參見[21])

其中φ是(M,g)上的任意光滑函數(shù).Yamabe不變量定義為

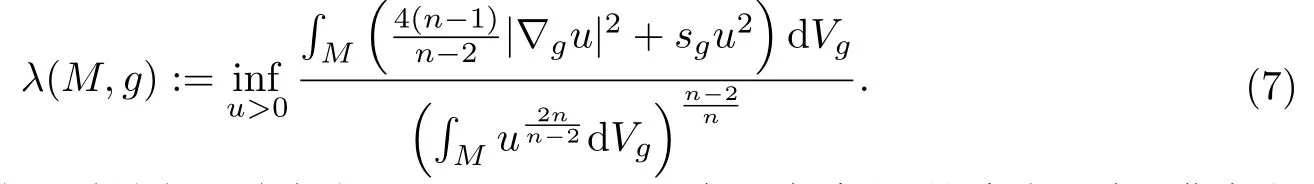
Paneitz算子對應(yīng)的正質(zhì)量定理首先由Humbert和Raulot在[9]中給出.這個定理在Q曲率方程中的作用與傳統(tǒng)的正質(zhì)量定理在Yamabe問題中的作用類似.在[10]中,作者用其他方法證明了類似的定理.當(dāng)n>4時,有如下Paneitz算子的正質(zhì)量定理.

定理2.1(參見[9,定理1.1])假設(shè)g是共形平坦的,n >4,λ(M,g)>0,Paneitz算子是正的,

上式取等號當(dāng)且僅當(dāng)(M,g)共形微分同胚于單位球面Sn.

§3 共形變換下的不變度量

令d(·,·)表示度量g下的距離,定義

定義n維Riemann流形(M,g)上的一類標(biāo)準(zhǔn)共形不變度量如下

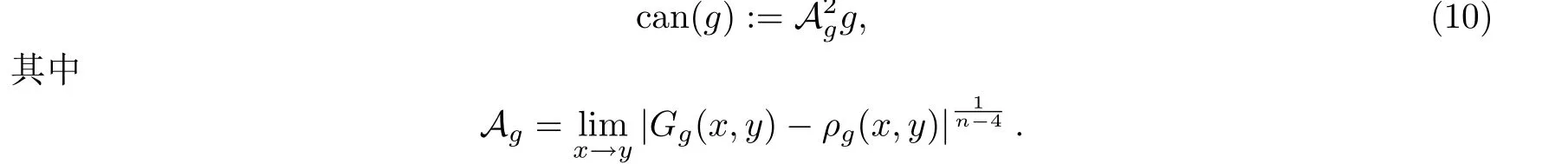
下面給出本文的主要結(jié)論.

定理3.1can(g)是一個C∞共形不變張量,即在共形變換(3)下,

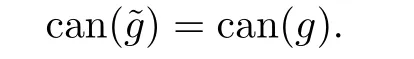
進(jìn)一步的,當(dāng)g是共形平坦的,n>4,λ(M,g)>0,Pg是正的,在M{y}上GP,g >0且(M,g)不共形微分同胚于單位球面Sn時,can(g)是一個C∞共形不變度量.

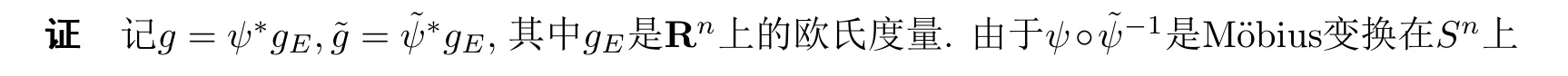
(參見[3,22]).因此,由Green函數(shù)在共形變換下的變換公式(6)以及(11),有

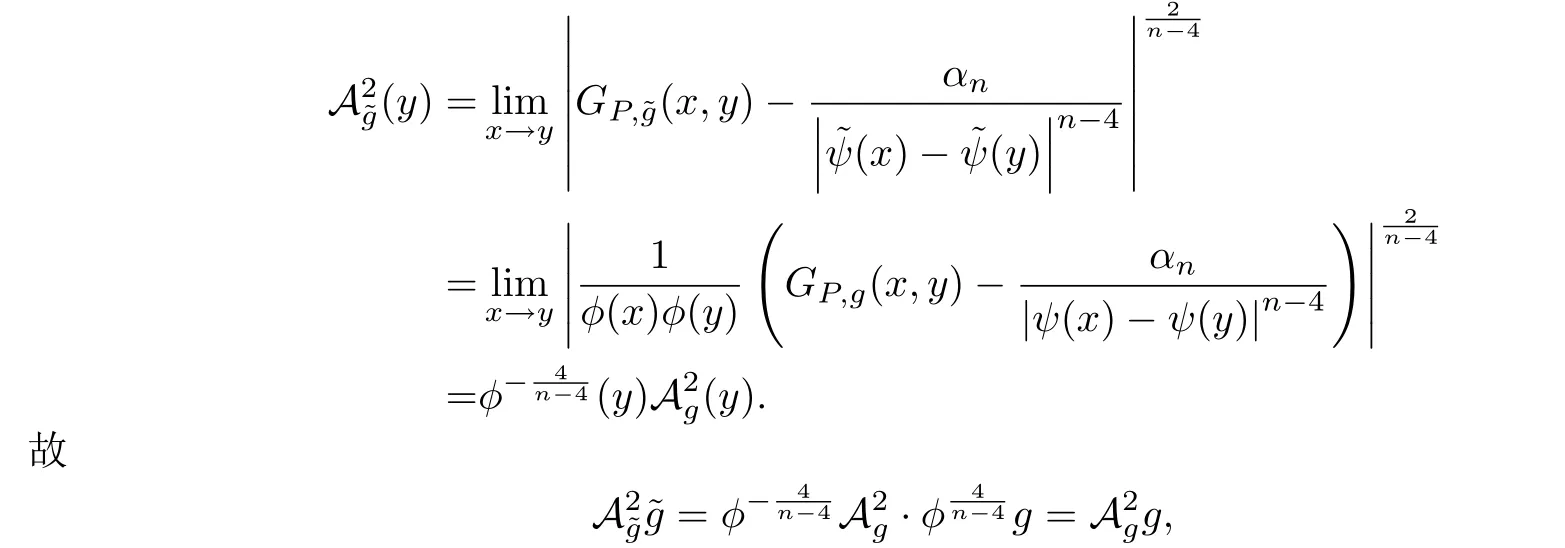
當(dāng)g是共形平坦的,n>4,λ(M,g)>0,Pg是正的且在M{y}上GP,g >0時,由Paneitz算子的正質(zhì)量(定理2.1)有

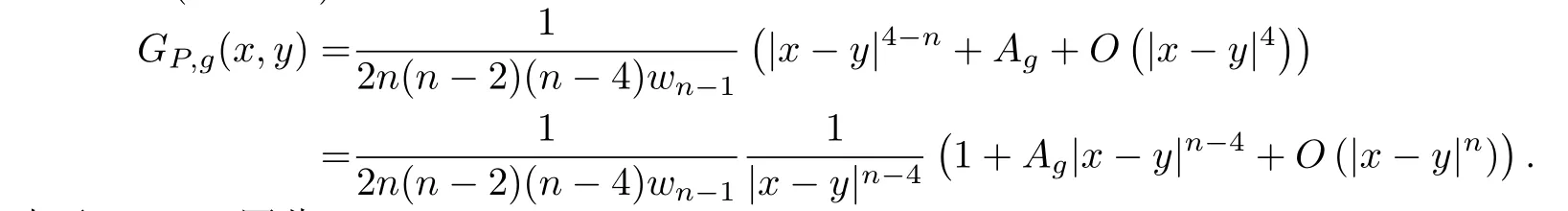
由于Ag >0,因此

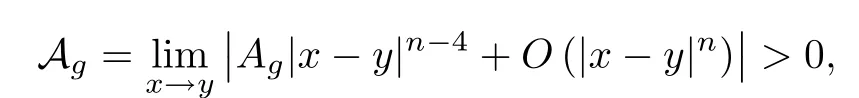
故can(g)進(jìn)一步的是一個C∞共形不變度量.

下面給出該共形不變度量的一些性質(zhì).

命題3.1(M1,g1),(M2,g2)為兩個連通的,緊的,滿足dimM1=dimM2>4,以及正質(zhì)量定理(定理2.1)的條件的Riemann流形,并且他們均不局部同胚于標(biāo)準(zhǔn)球面Sn.f:(M1,g1)→(M2,g2)為局部微分同胚,那么對于任意的X,Y ∈TM,有

其中Γ是一個覆蓋群且y ∈M1,f(x)/=f(y).

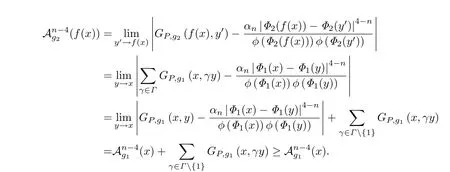
在上面第三個等式中,應(yīng)用了

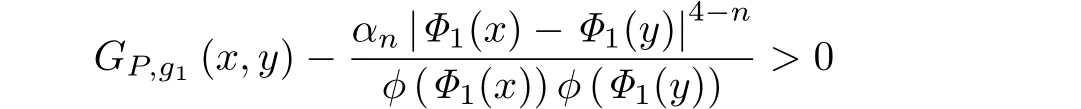
以及GP,g1(x,γy)>0兩個事實(shí).因此,對于任意的X,Y ∈TM,有

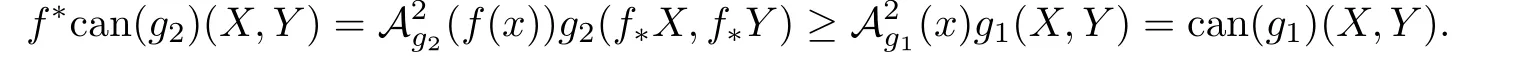
進(jìn)一步的,有如下推論.

推論3.1(M1,g1),(M2,g2)為兩個連通的,緊的,滿足dimM1=dimM2>4以及正質(zhì)量(定理2.1)的條件的Riemann流形,并且他們均不局部同胚于標(biāo)準(zhǔn)球面Sn.如果f是一個微分同胚,那么f?can(g2)=can(g1).