孫愛群,賈 高

(上海理工大學 理學院,上海 200093)

§1 引言

在參數(shù)λ>0且較小的情形下,考慮RN中具有Φ-Laplace算子和凹凸非線性項的擬線性橢圓型方程

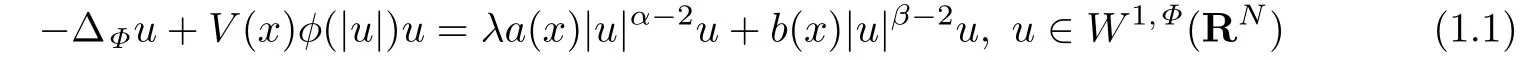
解的存在性和多重性,其中N ≥2,ΔΦu=div(φ(|?u|)?u)是Φ-Laplace算子,且

擬線性橢圓型方程具有較強的物理背景,是非牛頓流體,等離子物理,圖像處理等領(lǐng)域研究相關(guān)物理現(xiàn)象的重要模型,見[1-2].

過去幾十年里,在有界區(qū)域或全空間對含凹凸非線性項的Laplace方程(或p-Laplace方程)等相關(guān)問題得到廣泛研究,并取得許多重要結(jié)果(如[3-5]),而對于含有形如(1.1)中的更一般擬線性算子問題解的存在性研究雖有一些成果,比如[6-8],但是作者主要是在有界區(qū)域上進行研究的.

受[7]和[9]等文獻的啟發(fā),本文將在全空間RN中研究帶有Φ-Laplace算子和凹凸非線性項的擬線性橢圓型方程解的存在性和多重性.

現(xiàn)在給出函數(shù)φ和位勢函數(shù)V的基本假設(shè).φ ∈C2([0,∞),[0,∞)),并滿足以下條件:

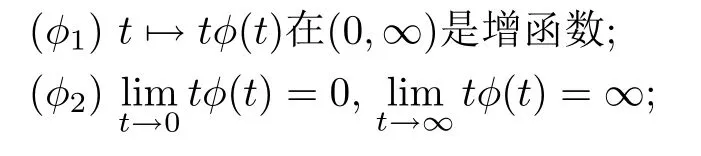
下面給出本文的主要結(jié)果.

定理1.1假設(shè)(φ1)-(φ3),(H),(V0)和(V1)成立,則存在Λ>0,當0<λ<Λ時,問題(1.1)至少有兩個非平凡解和,且Iλ()≤0,Iλ()>0,是基態(tài)解.

注記1.1與文獻[7]相比,本文是在全空間上研究問題(1.1)解的存在性,為此必須建立相關(guān)的緊嵌入定理.

§2 預(yù)備知識和主要引理

§3 Nehari 流形

§4 纖維映射的進一步性質(zhì)

§5 主要結(jié)果的證明

本節(jié)證明問題(1.1)存在兩個解.

定理1.1的證明該證明分為兩步:第一步證明當0<λ <λ1時,方程在上有一個解,第二步證明當0<λ<λ2時,方程在上也有一個解.

第一步:Iλ在Mλ上是有下界的,故在上也是有下界,從而存在極小化序列,滿足