淺談數(shù)列求和的常用方法
◇ 山東 史紅勇
1 公式法求和
利用常用求和公式求和是數(shù)列求和的基本方法.
例1設(shè){an}是公差不為0的等差數(shù)列,a1=2,且a1,a3,a6成等比數(shù)列,則{an}的前n 項(xiàng)和Sn=( ).
解析設(shè)等差數(shù)列的公差為d,因?yàn)閍1=2,則a3=2+2d,a6=2+5d.又因?yàn)閍1,a3,a6成等比數(shù)列,所以=a1·a6,即(2+2d)2=2(2+5d),整理得2d2-d=0.因?yàn)閐≠0,所以所以
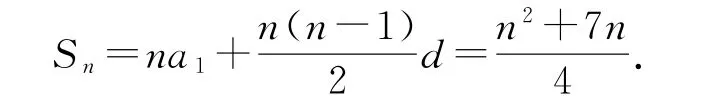
故選A.
2 錯(cuò)位相減法求和
將錯(cuò)位相減法用于數(shù)列求和,常見于求一個(gè)等差數(shù)列{an}和一個(gè)等比數(shù)列{bn}的對(duì)應(yīng)項(xiàng)之積構(gòu)成的數(shù)列{an·bn}的前n 項(xiàng)和.
例2已知{an}為等差數(shù)列,前n 項(xiàng)和為Sn(n∈N?),{bn}是首項(xiàng)為2的等比數(shù)列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通項(xiàng)公式;
(2)求數(shù)列{a2nb2n-1}的前n 項(xiàng)和(n∈N?).
解析(1)設(shè)等差數(shù)列{an}的公差為d,等比數(shù)列{bn}的公比為q.由b2+b3=12,得b1(q+q2)=12,而b1=2,所以q2+q-6=0.又因?yàn)閝>0,解得q=2,所以bn=2n.又因?yàn)閎3=a4-2a1,S11=11b4,則

聯(lián)立①②,解得a1=1,d=3,由此可得an=3n-2.所以數(shù)列{an}的通項(xiàng)公式為an=3n-2,數(shù)列{bn}的通項(xiàng)公式為bn=2n.
(2)設(shè)數(shù)列{a2nb2n-1}的前n 項(xiàng)和為Tn,由a2n=6n-2,b2n-1=2×4n-1,得a2nb2n-1=(3n-1)×4n,故
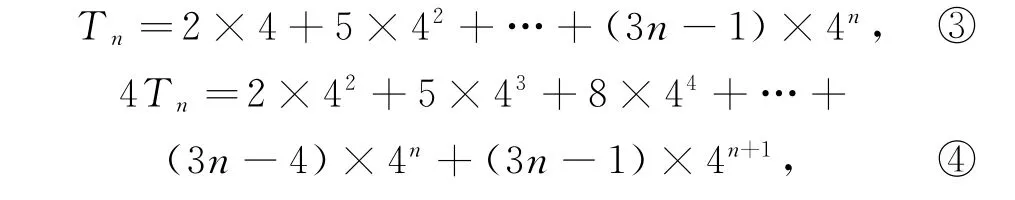
③-④,得
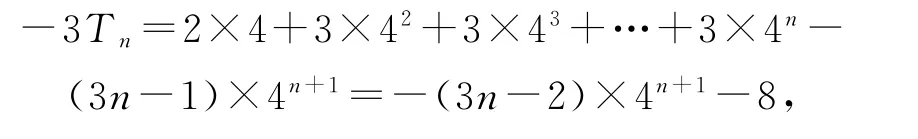
3 倒序相加法求和
若首尾距離相等的兩項(xiàng)和有其共性則可考慮運(yùn)用倒序相加法求和.
例3設(shè)則S=_____.
解析因?yàn)樗?/p>


①+②,得
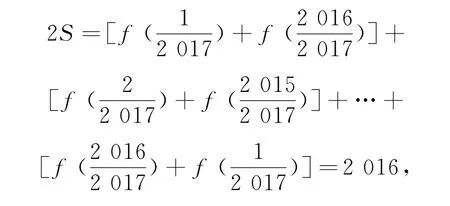
4 裂項(xiàng)相消法求和
如果數(shù)列{an}的每一項(xiàng)均可拆成兩項(xiàng)之差,并在求和時(shí)一些正負(fù)項(xiàng)可以相互抵消,只剩首尾若干少數(shù)項(xiàng),那么求{an}前n 項(xiàng)和可用裂項(xiàng)相消法.
例4已知等差數(shù)列{an}滿足(a1+a2)+(a2+a3)+…+(an+an+1)=2n(n+1).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)求{bn}的前n 項(xiàng)和Sn.
解析(1)設(shè)等差數(shù)列{an}的公差為d,當(dāng)n=1時(shí),a1+a2=4,當(dāng)n=2 時(shí),a1+a2+a2+a3=12,則4a2=12,a2=3,所以a1=1,d=a2-a1=2,所以an=1+2(n-1)=2n-1.
(2)由(1)可得

所以

5 分組法求和
如果數(shù)列{an}的各項(xiàng)均可寫成一些易求和的特殊數(shù)列的和或差,則可以把數(shù)列的每一項(xiàng)分解成兩項(xiàng)或多項(xiàng),或者把數(shù)列的項(xiàng)重新組合,使其轉(zhuǎn)化成兩個(gè)或多個(gè)等比數(shù)列(或等差數(shù)列)的和.
例5等差數(shù)列{an}的前n 項(xiàng)和為Sn,數(shù)列{bn}是等比數(shù)列,且滿足a1=3,b1=1,b2+S2=10,a5-2b2=a3.
(1)求數(shù)列{an}和{bn}的通項(xiàng)公式;
解析(1)設(shè)數(shù)列{an}的公差為d,數(shù)列{bn}的公比為q.由b2+S2=10,a5-2b2=a3,得
綜上,an=3+2(n-1)=2n+1,bn=2n-1.
(2)由a1=3,an=2n+1,得Sn=n(n+2),
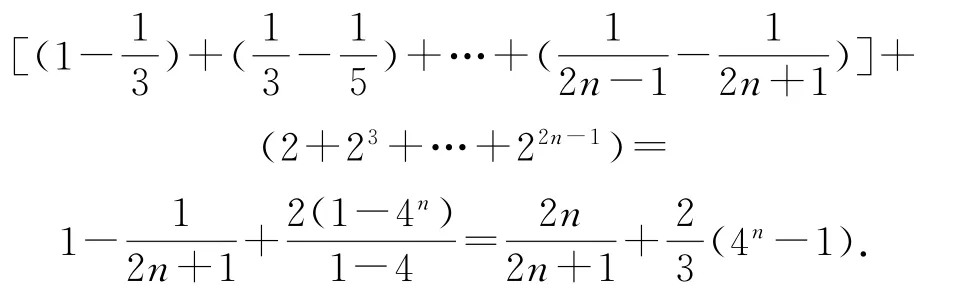
——由倒序相加想到倒序相乘

