,

New Material Industry Innovation Center,China Baowu Steel Group Co.,Ltd.,Shanghai 201999,China

Abstract: The application of four widely used anisotropic yield criteria,namely,Hill’48,Hill’90,Barlat’89,and Yld2000,on the formability analysis of an automobile aluminum sheet is investigated.The applicability and reliability of these four yield criteria are identified on the basis of uniaxial tensile and stamping tests of an aluminum covering panel by embedding the specimen in the corresponding finite element models.Results show that the strain distribution and safety margin of the aluminum sheet after stamping can be predicted with a high accuracy by applying Yld2000 compared to those subjected to the three other yield criteria.The significant effects of the anisotropic plastic characteristics of the aluminum sheet on stamping are discussed by applying the advanced simulation technology.

Key words: aluminum alloy sheet; anisotropic yield criteria; stamping; formability analysis

1 Introduction

With urgent social demands for improving fuel efficiency and reducing emissions,aluminum alloy sheets have been widely explored in automobile industries and considered potential substitutes for steel sheets because of their ability to lighten weight.However,their ductility is lower than that of mild steels,so special attention is required during stamping,which is a commonly used manufacturing process.The main step of the formability analysis of metal sheets during stamping is the analysis of cracking,wrinkling,and deformation deficiency; among these factors,cracking prediction and con-trolling are the most important.Fortunately,the complex deformation of aluminum alloy sheets during stamping can be monitored by applying a for-mation simulation technology,and trials and errors in the development of tools for an optimum performance can be reduced.Further efforts should be devoted to the discussion and determination of appropriate formability models and material constitutions to ensure simulation accuracy.

Ductile fracture,which is caused by the progres-sive degradation of material stiffness when plastic deformation reaches a certain limit,is an important issue that influences the formability of metal sheets[1].Among numerous complex ductile fracture criteria,which are developed for ductile fracture prediction,the forming limit curve (FLC) obtained via a forming limit test is practically significant and widely used in sheet formation.This important performance indicator can reflect limit deformation and is an effective tool to evaluate sheet metal formability and solve sheet metal stamping problems.KEELER et al.[2]pioneered the research in the field of FLC and emphasized that local deforma-tions should be considered.Inspired by this idea,HECKER[3],MARCINIAK[4],and NAKAZIMA et al.[5]applied different shapes of punches and speci-mens to determine the FLC.REES[6]showed that the FLC of automotive sheet metals was influenced by many factors,including material anisotropy,sheet orientation,thickness,strain history,and lubri-cation.Various theoretical models,particularly Swift’s[7],Hill’s[8],and M-K models[9],have also been developed on the basis of plastic instability for the calculation of FLCs.FATEMI et al.[10]utilized a modified M-K model to predict the forming limit of an anisotropic metal sheet subjected to normal and thickness shear stresses.LI et al.[11]also applied M-K theory to predict the FLC of aluminum-lithium (Al-Li) alloy 2198-T3 on the basis of different yield functions.Theoretical models are complex,and a profound knowledge of continuum mechanics is needed,so the FLC directly accepted from the test according to the actual forming conditions is still adopted by many engineers.

A material model is another important factor that affects the prediction accuracy of formability analysis.In phenomenological continuum-based models,the isotropic models of Tresca,Mises,Drucker,and Hershey were the most representative constitutions in the early period.Furthermore,many anisotropic yield criteria have been proposed to characterize the texture-induced anisotropy of many polycrystalline materials,for example,the well-known quadratic anisotropic yield criterion proposed by HILL in 1948[12].Since then,this area has been explored,and a series of efficient models have been proposed and numerically implemented into finite element platforms.Models are divided into two types on the basis of the structure of yield functions.One is in the form of a polynomial represented by the HILL and HU series[13-14].The other one is based on the linear transformation of the Cauchy stress tensor similar to the constitution proposed by BARLAT et al.in 2003[15].Among these yield criteria,Barlat’89[16]and Yld2000 are widely applied to the plastic formation of aluminum sheets to cover the “abnormal” anisotropy of aluminum alloys.Although the forma-bility analysis of metal sheets has been conducted by applying different yield criteria,the applicability and reliability of these yield criteria on the stamping of a certain aluminum component,which is beneficial to tool development,have been rarely reported.

In this study,four widely used yield criteria,namely,Hill’48,Hill’90,Barlat’89,and Yld2000,are applied to the formability analysis of an automobile aluminum sheet based on the fundamental mechanical properties obtained from uniaxial tensile and forming limit tests.The stamping of the aluminum covering panel of a certain car is investigated as a case to compare the differences in these criteria.Based on this process,a finite element (FE) model is established on the LS-DYNA platform.The accuracy of the predicted result of the four yield criteria is validated with the strain distribution data of a formed part,measured by a noncontact optical 3D deformation measuring system.Furthermore,two simple simulations are performed to investigate the significant effect of the anisotropic plastic behavior of aluminum sheets on stamping.

2 Review of the yield criteria of anisotropic materials

A yield criterion,which is an important part of an elastoplastic constitution model,can be interpreted as a surface in a stress space.The points located at the interior of the surface represent the elastic states of a material,whereas the points on the surface correspond to the plastic state.In this study,four typical anisotropic constitutions,namely,Hill’48,Hill’90,Barlat’89,and Yld2000,which are the most frequently used yield criteria and have been implemented in many kinds of commercial FE software,are used to describe the induced anisotrop-ic property of aluminum sheets.These criteria are briefly introduced in this section.

Hill’48 is an anisotropic yield criterion gener-alized from the Mises criterion.It is the simplest one in terms of a coordinate system associated with the axes of the orthotropic symmetry of materials.It is expressed with a quadratic function of the following type:

(1)

where,σ11,σ22,σ33,σ23,σ31andσ12are stress components;F,G,H,L,M,andNare constants specific to the anisotropy of a given material.These constants can be calibrated with the following ten-sile yield stresses and shear yield stresses associated with the principal anisotropy directions (X,Y,Z,R,S,andT).Consequently,six independent yield stresses along the principal anisotropy axes should be identified to completely describe the anisotropy of materials.

In the simulation of sheet metal formation,a yield criterion can be simplified in the form of plane stress,and four parameters are sufficient:

(2)

With anisotropy coefficients (r00,r45,r90) and yield stress along the rolling directionσ0,F,G,H,andNcan be easily obtained from the yield function:

(3)

Hill’48 has been verified in numerous experiments,and it is suitable for the plastic deformation of steel[17].Its advantages include its easily understood basic assumptions and requirement of a small num-ber of mechanical tests to determine relevant parameters.However,models cannot efficiently predict the yield stress in other directions because of the lack of the usage of the same number of yield stresses and anisotropy coefficients in identification.

To make the model more flexible,Hill added a high number of mechanical parameters (K1,K2,K3,K4) to the model and released a generalized form known as Hill’90[18]:

(4)

where

and

(8)

where,σYis the equivalent yield stress,and the exponentmis usually obtained through the yield stress in equibiaxial tension.For low-rmaterials,such as aluminum,m≈1.5,which is used as the value in this research.The anisotropic material constantsa,b,andcare obtained withr00,r45,andr90using the following equations:

and

(11)

This model can be utilized to describe the plastic deformation of metal sheets.However,it is not user friendly,so it is not as widely used as Hill’48.

To determine the influence of shear stress,Barlat and Lian successfully extended Hosford’s criteri-on[19]and proposed a more general form by expressing this criterion in a global system instead of principal directions.The yield criterion of plane stress in the Barlat’89 model is given as

(12)

(13)

The anisotropic material constantsa,c,h,andpcan be obtained withr00,r45,andr90:

(14)

and

(15)

pshould be calculated numerically.This model has a relatively good predictive ability for aluminum alloys without high anisotropy,but it lacks a direct and intuitive physical significance.

In 2003,Barlat developed an advanced anisotropic yield criterion that includes more coefficients and can precisely describe the anisotropy of sheet metals,such as aluminum alloy sheets,in yield stresses and Lankford coefficients.This plane stress yield function is expressed as follows:

(16)

where ,mis a material coefficient;X′1andX′2are the principal values ofX′;andX″1andX″2are the principal stresses ofX″.TensorsX′ andX″ are the linear transformations of the stress deviatorσ:

X′=L′σ,X″=L″σ

(17)

The associated linear transformationsL′ andL″ are determined with eight parameters (α1toα8):

and

(18)

These eight parameters can be calibrated with a uniaxial tensile test in three different directions.This model has a very flexible form and has been tested for different aluminum alloys.It can be used to accurately predict planar variations in the uniaxial yield stress and coefficient of plastic anisotropy.

3 Experiment

3.1 Test material

The test component investigated in this work is made of AA6111,which is widely used in automobile covers.Its thickness is 1.0 mm.The sheet is solution treated,quenched,and naturally aged to a substantially stable condition (T4 heat treatment).The chemical composition is shown in Table 1.

Table 1 Chemical composition of AA6111 alloy %

3.2 Uniaxial tension test

The specimens(Fig.1) are tested in three dif-ferent directions (rolling,diagonal,and transverse directions) in a tension machine.The strain rate is about 0.005 s-1,and at least three specimens are examined under each condition.

The engineering tensile curve stress is shown in Fig.2,and the tensile mechanical parameters derived from the test data are listed in Table 2.Similar to the yield stress,the flow stress of uniaxial tension in the rolling direction differs from that at 45° and 90°.

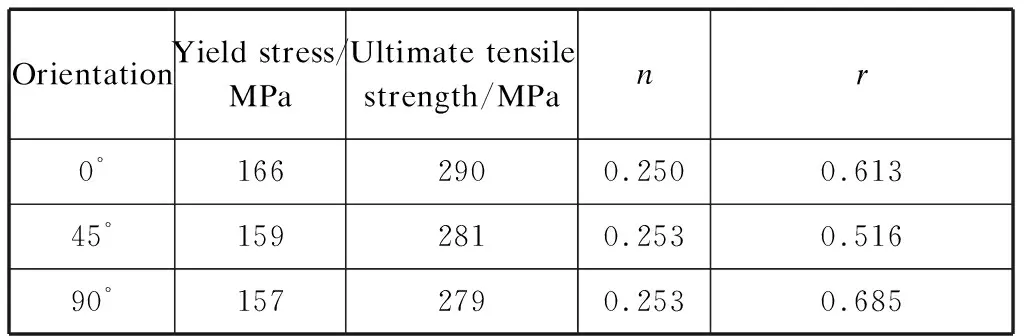
Table 2 Tensile mechanical parameters of AA6111-T4

3.3 Forming limit test

A punch stretching test (Fig.3) is performed to determine the FLC,where the specimen clamped between a blank holder and a die is stretched with a spherical punch with a radius of 61.0 mm.

The specimens with different widths are used to cover the strain domain as much as possible during aluminum sheet formation.The general shapes of these specimens are shown in Fig.4,and their sizes are listed in Table 3.The length of the specimens is oriented along the rolling direction of the aluminum sheet.

Grids of circles (Fig.5) are printed on an unde-formed sheet to measure the strain state at failure on sheet components.After a stretching test is conducted,the maximum values of the principal strainsε1andε2at failure can be determined by measuring the feature sizes of the ellipse on the sheet (Fig.6).

In Fig.6,d1andd2are the sizes of the major and minor axes of the ellipse on the deformed sheet,respectively.The mesh size is very small,sod1andd2can be simply measured under a microscope with a measuring system.Then,ε1andε2can be calcu-lated with the following formula:

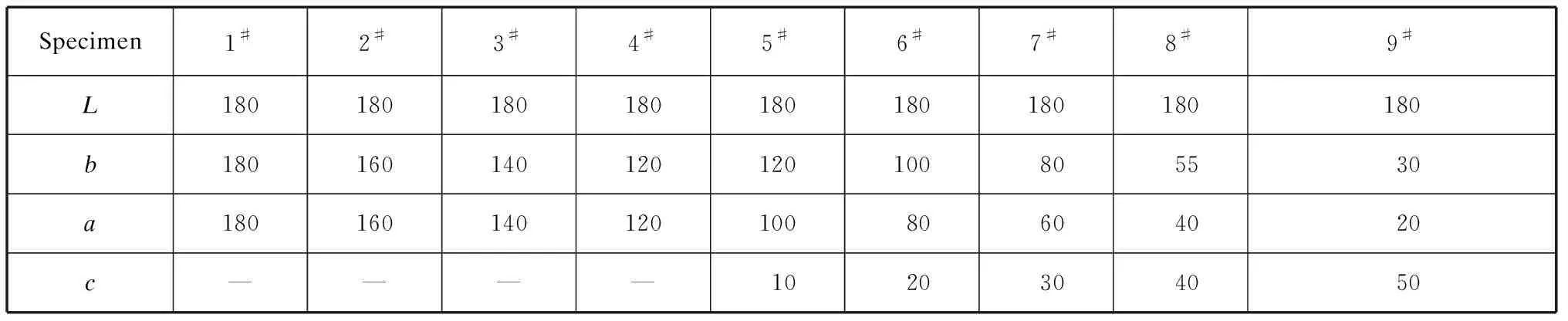
Table 3 Dimensions of the FLC specimens mm

(19)

The tested specimens are shown in Fig.7.The major strains against the minor strains obtained from these specimens at fracture are plotted in Fig.8,which illustrates the FLC of the investigated aluminum sheet.

3.4 Stamping test of the aluminum covering panel

In this research,the drawing operation of a certain aluminum covering panel is set as the case.In the stamping test,feeding is oriented along the rolling direction of the aluminum sheet with a blank holder force of 800 kN and a binder travel distance of about 80 mm after closing.

3.5 Strain distribution measurement

The deformation of the automobile aluminum sheet after stamping is determined with a noncontact optical 3D deformation measuring system.This coordinate measurement technique is famous in the field of metal sheet formation.It can be applied to analyze,calculate,and document the deformation of sheet metal parts.In comparison with traditional tape measurement,this coordinate measurement technique can be utilized to obtain the 3D coordinates of a component’s surface,the distribution of major and minor strains on the surface,and the reduction of material thickness.With the support of this system,many complex forming problems can be solved.Its most attractive aspect is its ability to compare the measured deformations with the material charac-teristics by adding the FLC and further verify numerical simulations.

Remarkable and complex plastic deformation occurs in the bottom corners of the investigated covering panel.In comparison with other areas,this special area likely cracks,and its strain distribution is worth studying.Therefore,this area is mainly explored in this research.

The detailed strain distributions are presented in the form of a cloud chart and a scatter diagram in Figs.9 and 10,respectively.The biaxial tension is the main deformation type in this corner,and an obvious compression exists in the addendum close to the binder,resulting in wrinkle formation.When the strain state is compared with the FLC of the original alu-minum sheet,the safety margin can be easily obtained.This margin is considered useful in engineering applications and defined as the minimum difference between the measuring strain and the forming limit along the vertical direction in the forming limit diagram(FLD).In most cases,the safety margin should be larger than 0.1,which can ensure production stability and improve product quality in a manufac-turing process.However,the safety margin of this area is 0.048,which indicates the possibility of cracking.As such,profile modification should be performed.

4 Simulation results and discussion

4.1 Comparison of the yield criteria

Combined with the uniaxial tensile test results along three different directions,the calibration methods are applied to determine the parameters of the four yield functions (Tables 4-7).

Table 4 Parameters of Hill’48 model MPa-2

Table 5 Parameters of Hill’90 model

Table 6 Parameters of Barlat’89 model (m=8)

In addition to the given yield function,the evolu-tion of the yield loci,which depend on flow rules and hardening laws,should be accurately and effi-ciently modeled[20].The flow rule is applied to de-scribe the relationship between applied stress and plas-tic strain increment.For most metallic materials,the associated flow rule,which states that the plastic poten-tial is the same as the yield function,is accurate for establishing a constitutive relationship[21].In com-parison with the initial yielding formulation,the subsequent yield locus may evolve with an obvious change in sizes,which can be described with hardening laws.In this research,the Voce equation is adopted and confirmed to be reliable in deter-mining the hardening behavior of an aluminum sheet in practice.This equation is expressed as follows:

σ=A+Be-Cε

(20)

Table 7 Parameters of Yld2000 model (m=8)

where,σis the stress,εis the strain,andA,B,andCare three constants.Material constants can be obtained with the least square curve fitting method based on the uniaxial tensile curve along the rolling direction.The three constantsA,B,andCare 383.5 MPa,217.7 MPa,and 10.1,respectively.

An FE model of tensile test (Fig.11) is established to validate the accuracy of the yield criteria.The experimental and predicted Cauchy stress and uniaxial tension along the three different directions are shown in Fig.12.The experimental result is consistent with the predicted Cauchy stress from Yld2000 after a large plastic strain is applied.However,for Hill’48,Hill’90,and Barlat’89,the experimental and predicted yield stress values along the diagonal and transverse directions significantly differ,although the predicted flow stress agrees well with the data along the rolling direction.This finding indicates that Yld2000 can better determine the anisotropic mechanical property of aluminum sheets than the other three yield criteria in terms of not only the coefficients of plastic anisotropy but also the flow stress in different directions.

The normalized yield loci predicted by the four criteria for the AA6111-T4 aluminum sheet are illustrated in Fig.13.The shapes of the yield loci under these criteria obviously differ.The yield loci of Hill’48 are smoother without a convex part than those of the three other yield functions.The normalized yield loci of Yld2000 are the smallest,whereas the normalized yield loci of Hill’90 are the largest.In the biaxial tension region,the predicted yield stress of Hill’90 is higher than that of the other criteria.

4.2 Application of anisotropic yield criteria in the stamping process

The FE model (Fig.14) is established on the basis of the platform LS-DYNA and the stamping test of the aluminum covering panel to investigate the application of the anisotropic yield criteria in aluminum sheet formation.

The detailed strain results of the left bottom of the covering panel are derived using the post-processing software to compare the accuracy of the different yield criteria in the formability analysis of the aluminum sheet (Fig.15).The strain results of Hill’49 and Hill’90 are quite different from the strain distribution obtained with the optical 3D deformation measuring system.As a result,the predicted safety margin considerably varies from the actual test value,which misleads a process designer and results in production cracking during manufacturing.On the contrary,the predicted strain distributions of the typical area of Barlat’89 and Yld2000 are fairly similar to the test strain result except the strain distribution of the addendum area close to the binder where the calculated compression strain is slightly larger.The simulation deviation of the strain level in the area of these two anisotropic yield criteria may be caused by the initial assumption that the plastic behavior of sheet metals is independent of loading directions,which do not model two important plastic features:one is the kinematic hardening feature[22],which particularly determines permanent softening with a constant stress offset,Bauschinger effect,and transient behavior under strain path reversal; and the other is the strength differential effect[23],which refers to noticeable differences between tension and compression.Nevertheless,the predicted safety margin of Yld2000 is close to the actual value.Therefore,Yld2000 is relatively effective in predicting plastic deformation during aluminum sheet stamping.Applying Yld2000 is better than using other complex yield criteria to describe the plastic deformation because it can be sufficiently and conveniently utilized by engineers to solve many complex forming problems and draw a better stamping process plan.

4.3 Effect of anisotropic plastic behavior on aluminum sheet formation

The anisotropic plastic behavior of aluminum sheets significantly affects stamping,which leads to an obvious variation in strain distribution although strength is similar.Two simple simulation studies are performed to investigate this important aspect.

In one of the simulations,the differences between an aluminum sheet and an isotropic material during stamping are analyzed.The isotropic material is obtained by reasonably modifying the material param-eters of the received anisotropic aluminum sheet.In this modification,the anisotropic coefficients (r) of the thickness along three different directions are set to 1.0,and the yield stress and the hardening curve are the same as those of the received aluminum sheet.The strain results of the isotropic material after stamping are shown in Fig.16.The magnitude of the predicted maximum principal strain decreases from 0.175 to 0.156,and all the dots in the principal strain plane,which represent the strain state of the elements in the FE model,move toward the negative direction of the minor principal axis.As a consequence,the area with the highest cracking possibility in the anisotropic sheet is at the state of uniaxial tension instead of biaxial tension.

In the other simulation,the effect of feeding direction on formation is based on the anisotropic feature of the received aluminum sheet.The strain distribution of the typical area of different material orientations is obtained by changing the feeding direction of the aluminum sheet in the stamping FE model where Yld2000 is the material model (Fig.17).The strain distribution of the sheet feeding at the diagonal and transverse directions is similar to the one feeding at the rolling direction.The obvious difference,which is emphasized by the blue blank in the picture,shows that the thickening level slightly higher in the relevant position than in the original feeding direction.In Fig.18,the thickening area of the aluminum sheet fed along the diagonal and transverse directions is larger than that along the other directions.As such,the weak anisotropic feature of the aluminum sheet results in the similarity of the strain results in different feeding directions.If the anisotropic feature is strong,the initial material orienta-tion possibly influences the formation results.

5 Conclusions

In this study,the applicability and reliability of four widely used yield criteria on the formability analysis of aluminum sheet formation are identified on the basis of the stamping of an aluminum covering panel.Based on the results,the following conclusions can be drawn:

(1) The anisotropic characteristics of aluminum alloy sheets in uniaxial tensile tests can be better described with Yld2000 than with the three other anisotropic yield criteria,namely,Hill’48,Hill’90,and Barlat’89.

(2) The strain distribution and safety margin of aluminum sheets after stamping can be predicted with reasonable accuracy by applying Yld2000.

(3) The anisotropic plastic behavior of aluminum sheets significantly affects stamping.Consequently,a significant discrepancy in strain distribution is observed although strength is similar.