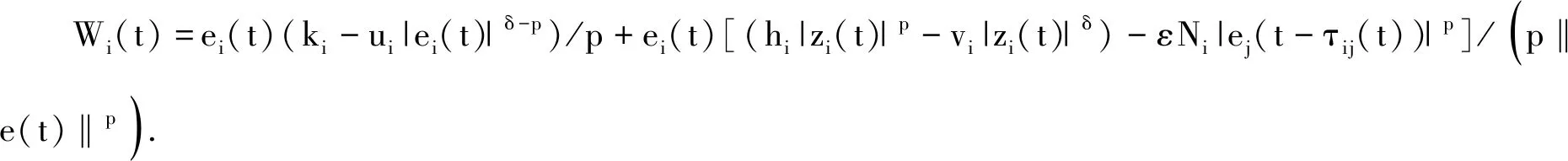蒲 浩, 冉 杰, 潘永會, 張轉(zhuǎn)周, 黃建文

(1. 遵義師范學院數(shù)學學院, 貴州 遵義 563006; 2. 西南大學數(shù)學與統(tǒng)計學院, 重慶 400715)

自競爭型神經(jīng)網(wǎng)絡(luò)首次被提出以來, 由于競爭型神經(jīng)網(wǎng)絡(luò)模型在不同領(lǐng)域有重要的應(yīng)用而受到廣泛關(guān)注[1].近年來, 競爭型神經(jīng)網(wǎng)絡(luò)的控制同步理論[2-3]以及多重因素影響下競爭型神經(jīng)網(wǎng)絡(luò)依賴于系統(tǒng)初值在無限時間的控制同步問題[4-5]得到了廣泛研究.Shi等[5]研究了具有不同時標和反映擴散項隨機競爭神經(jīng)網(wǎng)絡(luò)實現(xiàn)同步的條件; Ryan[6]提出了神經(jīng)網(wǎng)絡(luò)依賴于初值在有限時間內(nèi)穩(wěn)定性理論; Li等[7]研究了依賴于系統(tǒng)初值的混合時滯和不同擾動競爭神經(jīng)網(wǎng)絡(luò)在有限時間內(nèi)的同步.為了解決神經(jīng)網(wǎng)絡(luò)系統(tǒng)的初值事先不能準確地獲得或很難獲得的問題, Polyakov[8]提出了獨立于系統(tǒng)初值的固定時間穩(wěn)定性理論; Wan等[9]研究了時滯Cohen-Grossberg型神經(jīng)網(wǎng)絡(luò)的魯棒固定時間同步.本文擬通過固定時間穩(wěn)定性理論, 研究具有變時滯隨機競爭神經(jīng)網(wǎng)絡(luò)在固定時間的控制同步.

1 模型及預備知識

考慮具有變時隨機競爭型神經(jīng)網(wǎng)絡(luò)模型

(1)

其中n為神經(jīng)元數(shù)目,p為恒定的外部刺激數(shù)目;ci為神經(jīng)元時間常數(shù);ε為短期記憶狀態(tài)的時間尺度;fj(·)表示t時刻第j個神經(jīng)元的輸出量,xi(t)表示t時刻第i個神經(jīng)元的狀態(tài);aij,bij分別表示第i個和第j個神經(jīng)元之間的連接強度;τij(t)表示t時刻第i個神經(jīng)元與第j個神經(jīng)元之間的信號轉(zhuǎn)換時滯, 滿足0≤τij(t)≤τij;mil(t)表示突觸效率;Hi表示外部刺激強度;αl,βi為常數(shù).

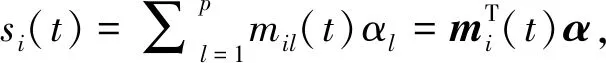
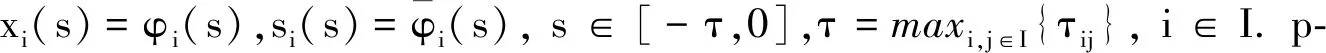
把系統(tǒng) (1) 作為主驅(qū)動系統(tǒng),并引入響應(yīng)系統(tǒng)

(2)

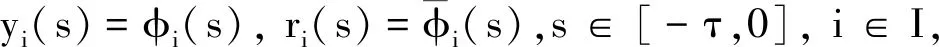
定義誤差系統(tǒng)為ei(t)=yi(t)-xi(t),zi(t)=ri(t)-si(t), 根據(jù)系統(tǒng)(1)和系統(tǒng)(2)有

為實現(xiàn)驅(qū)動系統(tǒng)(1)和響應(yīng)系統(tǒng)(2)在固定時間同步,構(gòu)造外部輸入控制Ui(t)=ei(t)(ki-ui|ei(t)|δ-p)/p+ei(t)(hi|zi(t)|p-vi|zi(t)|δ)/(p‖e(t)‖p)-ωiei(t)(|ei(t)|λ+|zi(t)|λ)/(np‖e(t)‖p)-εNiei(t)|ej(t-τij(t))|p/(p‖e(t)‖p), 其中ki,ui,hi,vi,ωi,Ni都是常數(shù), 0<δ<1.

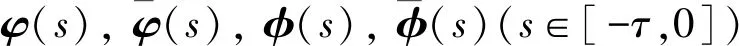
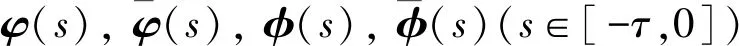
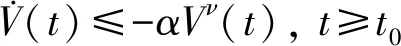
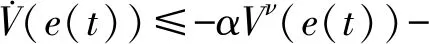
2 主要結(jié)果

定理6若(H1)(H2)成立且Xi+ki≤0,Qi+hi≤0,i∈I, 則驅(qū)動系統(tǒng)(1)和響應(yīng)系統(tǒng)(2)在恰當?shù)耐獠枯斎肟刂芔i(t)下, 在固定時間T=εp/[a(p-δ)]+2λ/p-1nλ/pεp/[b(λ-p)]內(nèi)同步, 其中a>0,b>0,0

注1文獻[11]是具有不同時標和隨機擾動的競爭型神經(jīng)網(wǎng)絡(luò), 文獻[12]是混合變時滯的隨機競爭型神經(jīng)網(wǎng)絡(luò), 系統(tǒng)均當時間t→+∞時才能實現(xiàn)自適應(yīng)同步.

注2在響應(yīng)系統(tǒng)(2)中存在隨機擾動項, 要使定理1中的條件Xi+ki≤0,Qi+hi≤0成立, 則需要外部輸入控制Ui(t)中的ki,hi的絕對值變得更大, 故隨機擾動項的存在對神經(jīng)網(wǎng)絡(luò)在固定時間的同步有抑制作用.

注3文獻[13]是依賴于系統(tǒng)初值的混合時滯競爭型神經(jīng)網(wǎng)絡(luò)在有限時間內(nèi)的同步問題,由推論1可知, 文獻[13]中的結(jié)論是本文中的一種特殊情況.