YE Liu, DU Mingming, WANG Dong

(School of Physics & Material Science, Anhui University, Hefei 230601, China)

Abstract:Uncertainty relations provide constraints on how well the outcomes of incompatible measurements can be predicted and fundamental to our understanding of quantum theory. They have practical applications in cryptography and witnessing entanglement. Here, the authors explored how Unruh effect would affect quantum-memory-assisted entropic uncertainty relation (QMA-EUR) for a pair of maximally entangled Unruh-Dewitt detectors when one of them was accelerated and coupled to a massless scalar field. The result showed that while the amount of uncertainty was increased in low accelerations, it was reduced in higher accelerations and had a nontrivial behavior acquiring its maximum value at a certain acceleration. The mechanism of these phenomena were explored by using two dissimilar methods.

Keywords: uncertainty relation; Unruh effect; quantum correlation

0 Introduction

In quantum mechanics, we predict precisely the outcomes of an observable by preparing eigenvectors corresponding to the state of the measured system. However, the ability to predict the precise outcomes of two conjugate observables for a particle is restricted by the uncertainty principle which can be expressed in different forms, i.e.,Heisenberg’s uncertainty relation[1]and the entropic uncertainty relation (EUR)[2]. It has burst out various remarkable applications[3]. Beyond their foundational appeal, uncertainty relation has also become an important tool in quantum information theory, particularly entropic formulations[3-8].

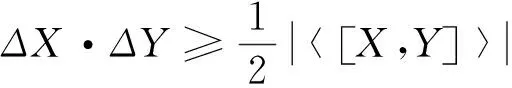
(1)

whereXandYwere observables,H(X(Y)/B) was the conditional von Neumann entropy of the postmeasurement state

ρX(Y)B=∑x(y)(|x(y)〉〈x(y)|?IρAB|x(y)〉〈x(y)|?I)

(2)

andH(A/B) was the conditional von Neumann entropy. It provides a bound on the uncertainties of the measurement outcomes that depend on the amount of entanglement between the measured particle,A, and the quantum memory,B. As is well known that -H(A/B) gives the lower bound of the one-way distillable entanglement[4]. From the above relation, it is easy to conclude that the outcomes can be predicted accurately whenAandBare in the state of maximal entanglement. On the other hand, ifAandBare not entangled, the inequality can be reduced to

(3)

The uncertainty principle in the presence of memory is important for cryptographic applications and witnessing entanglement[3-4]. It has been recently confirmed experimentally[9, 13], and has ignited interests of people on investigating its potential applications from various aspects[3, 4-8, 14-15]. Furthermore, such uncertainty relations are also important for basic physics and quantum information processing[3].

As is well known that quantum objects are inevitably in contact with environments and a consequence of the interaction is decoherence or dissipation. So the nature of environment plays a key role in dominating the evolution of the quantum system, as well as the uncertainty relation. There have been diverse efforts to investigate the dynamics of the uncertainty relation under noise environment[15-17]. On the other hand, the general theory of relativity and quantum mechanics are the foundation of modern theoretical physics. The integration of quantum information and the general relativity gives birth to the theory of the relativistic quantum information, opening up a new way to understand the information paradox when black holes are involved. In particular, noises resulting from the motions of observers or gravitational field, which directly relate to the nature of spacetime and allow us to incorporate the concepts of quantum information into relativistic settings, become a very important branch of quantum noisy channels. Therefore, diverse efforts have been made to investigate the dynamics of teleportation fidelity[18], quantum entanglement[19-24], quantum discord[25], Bell nonlocality[26], and some other information quantities under relativistic motion[27-29].

Consequently,it will be interesting to study how the relativistic effect affects the uncertainty relation. Several questions naturally arise: Will the motions of observers or gravitational field only increase the amount of uncertainty because of disentanglement? Is quantum correlation the only key factor for this uncertainty relation under the motions of observers or gravitational field? However, only a few authors have attempted to address this problem[30-33]. Feng et al.[30]have investigated an uncertainty game in noninertial frame, and showed an increasing uncertainty in bipartite system of free Dirac field, and a periodic evolution of uncertainty for localized quantum system restricted in cavities, providing an efficient relativistic entanglement witness that could be detected experimentally; They have also explored the entropic uncertainty relation in the curved background outside a Schwarzschild black hole[31], and found that Hawking radiation introduces a nontrivial modification on the uncertainty bound for particular observer; Jia et al.[32]have studied the entropic uncertainty relation under the decoherence rooting in vacuum field fluctuation in the de Sitter space and showed that the thermal nature of the de Sitter space could surely increase the uncertainty and finally the uncertainty reached a maximal value; Wang et al.[33]have investigated quantum-memoryassisted entropic uncertainty relation (QMA-EUR) when the particle to be measured stayed at an open system, and another particle was treated as quantum memory under a noninertial frame. They concluded that, firstly, the noises and the Unruh effect can both increase the uncertainty; secondly, the uncertainty is more affected by the noises than by the Unruh effect from the acceleration; thirdly, unital noises can reduce the uncertainty in long-time regime. In this work, we study quantum-memory-assisted entropic uncertainty relation between a pair of Unruh-Dewitt detectors when one of them is accelerated. The detectors are modeled by two-level semiclassical atoms with fixed energy gap and are designed to interact locally with the neighbor scalar fields. We assume that Alice’s detector is always switched off and remains stationary, while Bob’s detector moves with a constant acceleration and interacts with the massless scalar field. The results shows that (i) for null acceleration, the amount of uncertainty differs from zero; (ii) the amount of uncertainty approaches the unity in the limit of an infinite acceleration; (iii) the curves of uncertainty are not monotonic and have a nontrivial behavior acquiring its maximum value with the acceleration increasing. In order to understand the physical origin of the above phenomena, we give two possible ways (the entanglement between the qubits and the field, and the competition between quantum correlations and the minimal missing information of a single particle after local measurement on another one) to explain the above phenomena. Compared with other works[30-33], our model avoids a physically unfeasible detection of global free models in the full space and can avoid the use of cavities in the state preparation process.

The outline of the paper is as follows. In Sec.1, we introduce our two-level detector model. In Sec. 2, we investigate the effect of Unruh effect for quantum-memory-assisted entropic uncertainty relation. In Sec. 3, we give the influence of the entanglement between the qubits and the field (QFE), and quantum correlation on this uncertainty relation. The conclusions are given in the last section.

1 Two-level detector model

In this section, we briefly introduce the qubit system considered here (Refs. [18, 25-26, 29] for more details).

Our qubits are modeled as two-level semiclassical detectors[34]with energy gapΩthat is introduced by Unruh et al[35]. The detector proper Hamiltonian is defined as

HR=ΩR?R,

(4)

whereR(R?) are the transition operators for the qubit energy eigenstates:R|0〉=R?|1〉=0,R|1〉=|0〉 ,R?|0〉=|1〉 with |0(1)〉 are the corresponding unexcited (excited) energy eigenstate, respectively. The detector is coupled to a massless scalar fieldφ, which satisfies the Klein-Gordon equation[36]

aaφ=0,

(5)

through the Hamiltonian

(6)

whereε(t) is a smooth compact-support real-valued function, which keeps the detector switched on for a finite amount of proper timeΔ[37],g≡det(gab) with the Minkowski metricgab,xare coordinates defined on the Cauchy surface and Σt=constassociated with some suitable time-like isometry. Here,ψ(x) is a coupling function, which models the fact that the detector only interacts with the field in a neighborhood of its world line. Utilizing Eqs. (4)-(6), the total Hamiltonian can be cast as

(7)

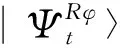
(8)

whereTis the time-ordering operator and

(9)

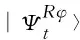
(10)

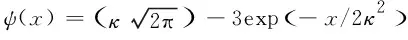
(11)

where

(12)

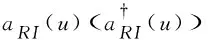
2 The effect of Unruh effect for quantum-memory-assisted entropic uncertainty relation

We assume that two observers, Alice and Rob, each of them possesses an Unruh-Dewitt detector modeling through a two-level noninteracting atom.

In our uncertainty game, we focus on the uncertainty game model illustrated in Ref.[4]: Rob sends qubitA, initially entangled with another qubitB(quantum memory), to Alice. Then, Rob begins to move with an accelerationaalong thexaxis for the finite amount of proper timeΔ. The world line of Rob’s qubit is given byt(τ)=r-1sinhrτ,x(τ)=r-1coshrτ,y(τ)=z(τ)=0 , whereτandrare the qubit proper time and acceleration. Here, (t,x,y,z) are the usual Cartesian coordinates of Minkowski space-time. The detectors are designed to be switched on only when they are accelerated. Thus, Alice’s inertial qubit only interacts with the scalar field indirectly through Rob’s detector. In the meantime, Alice measures eitherXorYand announces her measurement choice to Rob. Eq. (1) captures Rob’s uncertainty about Alice’s measurement outcome. As mentioned before, Rob sends Alice a qubitA, initially entangled with another his quantum memoryBwhich has the form as

(13)

where |0〉A(chǔ)(R)and |1〉A(chǔ)(R)represent the unexcited and excited states of Alice’s (or Rob’s) detector, respectively. The initial state of the detector-field system has the form

?|0M〉,

(14)

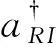
(15)

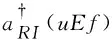
(16)

where

(17)

Here,w(t,x,y,z)=(-t,-x,y,z) is a wedge reflection isometry that makes a reflection fromηin the Rindler region I toη°win the Rindler region II. By tracing over the degrees of freedom of the external field, we obtain the density matrix

(18)

(19)

Noting that the detector is allowed to be flipped only once or never, we can see from the asymptotic state Eq. (19) that in the infinite acceleration limit Bob’s detector must necessarily flip, i.e., no flip is not an option in this case.

By employing a pair of Pauli operatorsσxandσzas the incompatibility,X=σxandY=σz, we have the post measurement states

(20)

The eigenvalues can be easily calculated and the corresponding von Neumann entropy are

(21)

and

H(ρtσzR)=-2αlog2α-βlog2β-γlog2γ,

(22)

whereHbinis denoted as a binary entropy withHbin=-xlog2x+(1-x)log2(1-x) .

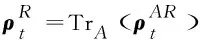
2[(α+β)log2(α+β)-(α+γ)log2(α+γ)]+1.

(23)

By numerical calculation, we find that (i) when the effective couplingv2=0 , we haveU=0 implying that the measuring outcome can be accurately predicted by the observer. (ii) for low enough accelerations and fixed the effective couplingv2, the uncertainty keeps its value close to zero, but differs from zero (see Fig.1). This is because for very low accelerations the temperature of the Unruh thermal bath is small containing, thus, quite few particles with proper energyΩable to interact with the detector. The reason why the value of uncertainty differ from zero for arbitrarily smallais that even inertial detectors have a nonzero probability of spontaneously decaying (along the nonzero time intervalΔ) with the emission of a Minkowski particle, which carries away some information. (iii) the uncertainty has a nontrivial behavior acquiring its maximum value. It is different previously results[30, 33]. (iv) for arbitrarily large accelerations, where the detector experiences high Unruh temperatures, we haveU=1 indicating that the qubits are still correlated but not entangled, as it can be seen directly from Eq. (19).

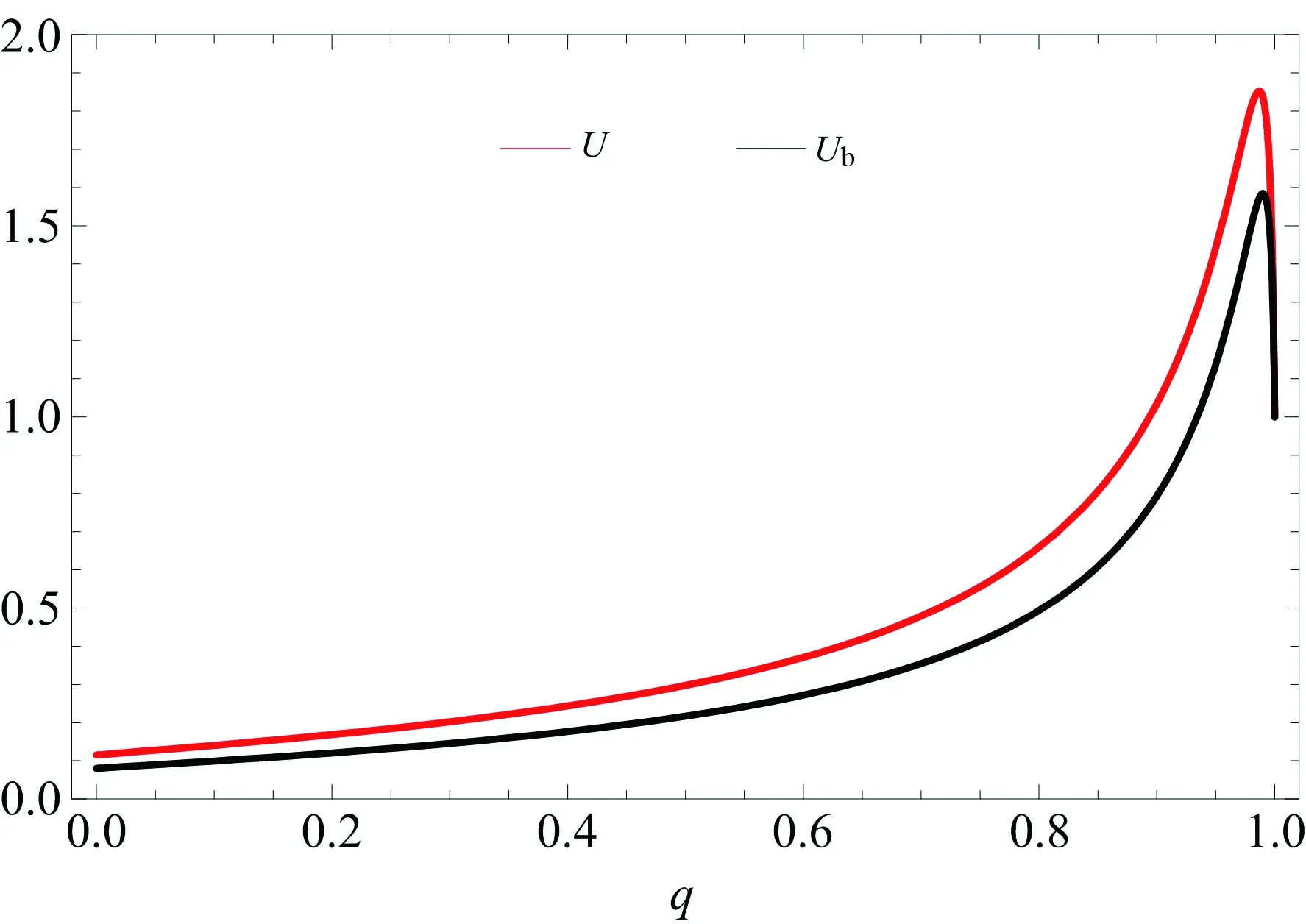
Fig.1 The graph exhibits the uncertainty and the lower bound of uncertainty as a function of acceleration parameter q

(α+β)log2(α+β)+(α+γ)log2(α+γ).

(24)

As depicted in Fig.1, we note that for null acceleration and the fixed effective couplingv2,U>Ub. As the above reason, inertial detectors have a nonzero probability of spontaneously decaying (along the nonzero time intervalΔ) with the emission of a Minkowski particle, which affects the low bound of uncertainty. Moreover, the lower bound of entropic uncertainty has almost the same variation tendency with the uncertainty (U). In addition, for arbitrarily large accelerations, the uncertainty can be equivalent with the lower bound of entropic uncertainty (U=Ub=1 ). From Eq. (24), we note that ifU=H(X/R)+H(Y/R)<0 , thenH(A/R)<0 , and henceρARis entangled. As a negative conditional entropy is a signature of entanglement. Berta et al.[4]has explained how it can be applied to the task of witnessing entanglement. Especially, Hu et al.[8]have first related quantum-memory-assisted entropic uncertainty relation (QMA-EUR) to quantum teleportation, and showed geometrically that any two-qubit state which lowers the upper bound of this uncertainty relation is useful for teleportation. We believe that our results are useful for studying teleportation under Unruh effect.

In order to probe the nature of the uncertainty evolution, we will analyze the influence of the entanglement between the qubits and the field (QFE) and quantum correlation on this uncertainty relation.

3 Explanation for the above phenomena

3.1 The influence of the entanglement between the qubits and the field (QFE) on this uncertainty relation

In this section,we will try to explain the phenomenon represented above from the perspective of quantum entanglement.

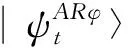
(25)

3.2 The influence of quantum correlation on this uncertainty relation

In this section, we will try to explain the phenomenon represented above from the perspective of quantum correlation beyond entanglement. The quantum correlation of a two-qubit composite system composed ofAandBis quantified[38]by

(26)

Fig.2 The graph exhibits the uncertainty, the lower bound of uncertainty and the entanglement between the two-qubit system and the field as a function of acceleration parameter q

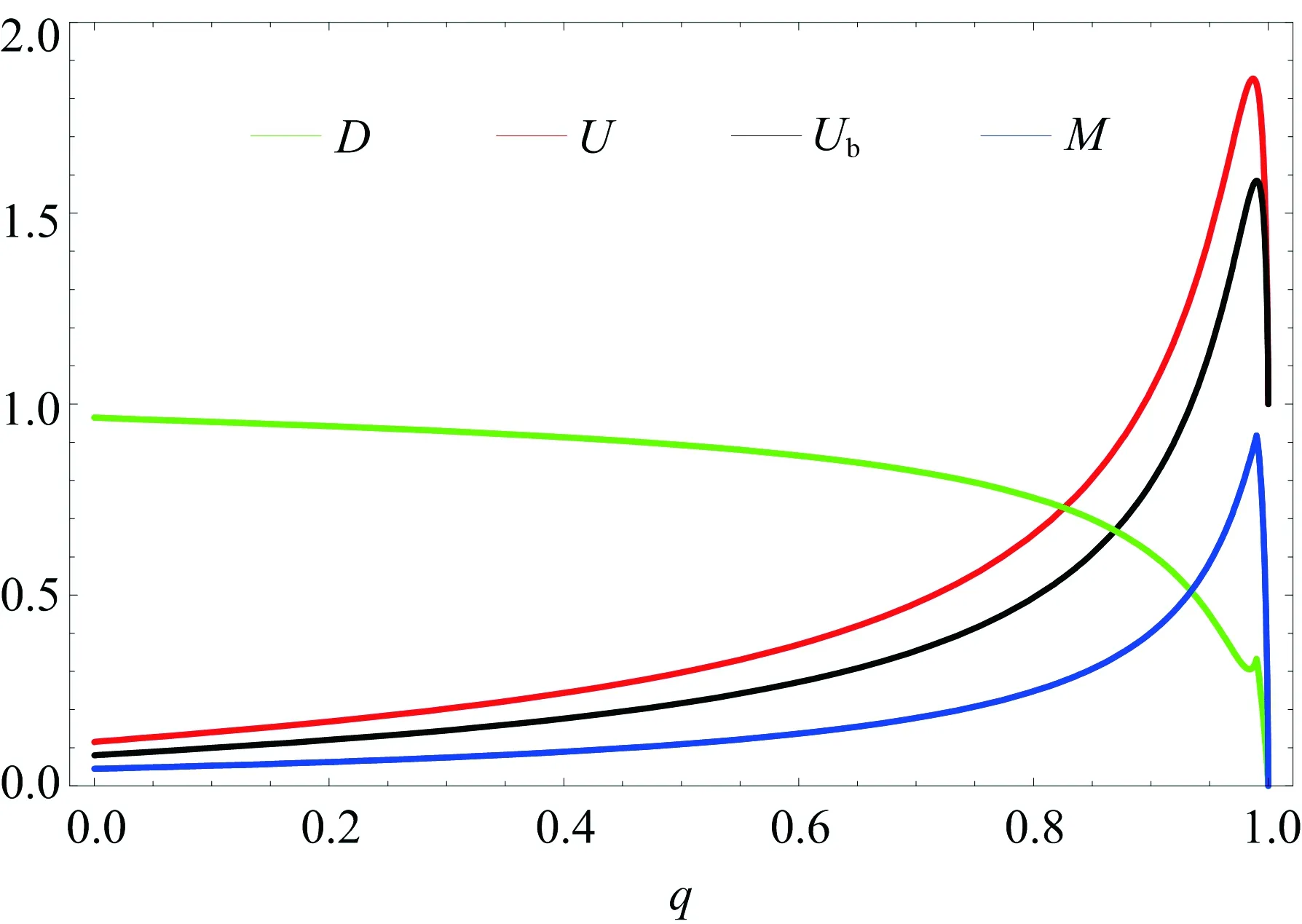
Fig.3 The entropic uncertainty( U and Ub ), quantum discord (D) and the minimal missing information (M) as a function of acceleration parameter q

In order to understand the physical origin of the above phenomena, we relate the lower bound of Eq. (1) to the quantum correlation (Eq. (26)). Therefore, we have[15]

(27)

Apparently, the uncertainty is related to the discrepancy betweenMandD, not just the quantum correlations only, and it is decided by the competition between quantum correlations and the minimal missing information of a single particle after local measurement on another one. For the operational interpretations ofMandDsee Refs. [15, 39-40]. In Fig.3, it clearly shows that the missing information by local measurements may be reduced, which in turn lowers the uncertainty.

4 Conclusion

Here, quantum-memory-assisted entropic uncertainty relation (QMA-EUR) for two entangled Unruh-Dewitt detectors is studied when one of them is accelerated and interacted with a massless scalar field. We employ the Unruh-Dewitt detector model, which interacts locally with the neighbor external field. The following conclusions are obtained: (i) for null acceleration, the amount of uncertainty differs from zero; (ii) the amount of uncertainty approaches the unity in the limit of an infinite acceleration; (iii) the curves of uncertainty are not monotonic and have a nontrivial behavior acquiring its maximum value with the acceleration increasing. For the above phenomena, it can be explained by two possible ways (the entanglement between the qubits and the field, and the competition between quantum correlations and the minimal missing information of a single particle after local measurement on another one). Aside from its fundamental significance, our result has an impact on the development of future quantum technologies (e.g. witnessing entanglement[4]and teleportation[8]under Unruh effect). In addition, we know that an accelerated observer in the Minkowski vacuum corresponds to static observers outside a black hole in the Hartle-Hawking vacuum. Similarly, a static observer in the Minkowski space-time corresponds to a free-falling observer in the Schwarzschild space-time. Therefore, the analysis used to derive the results of our manuscript can be applied to study quantum-memory-assisted entropic uncertainty relation under the influence of Hawking radiation.